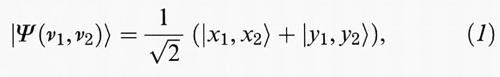Meccanica quantistica, verifiche sperimentali
Meccanica quantistica, verifiche sperimentali
SOMMARIO: 1. Il dibattito fra Bohr e Einstein: a) meccanica quantistica e probabilità; b) l'argomento di Einstein, Podolsky e Rosen; c) la separabilità quantistica è il nocciolo della discussione; d) le reazioni. □ 2. Il teorema di Bell: a) un passo avanti concettuale; b) le ineguaglianze di Bell e il conflitto con la meccanica quantistica. □ 3. Il passaggio all'esperienza: a) situazioni eccezionali; b) esperienze di prima generazione; c) risultati incontestabili; d) esperimenti con polarizzatori variabili; e) una nuova generazione di esperimenti. 4. Conclusione. □ Bibliografia.
1. Il dibattito fra Bohr e Einstein
a) Meccanica quantistica e probabilità.
La meccanica quantistica è stata formulata nelle sue versioni moderne nel 1925-1926 da E. Schrödinger da una parte (meccanica ondulatoria) e da W. Heisenberg, P. Jordan e M. Born dall'altra (meccanica delle matrici). Dopo che fu dimostrata l'equivalenza fra queste due formulazioni, dapprima dallo stesso Schrödinger e poi da J. von Neumann, il formalismo non poneva più problemi, anche se la sua interpretazione avrebbe continuato a sollevare discussioni senza fine.
Il punto più controverso era il carattere probabilistico delle predizioni della teoria quantistica messo in luce da Born già nel 1926. Consideriamo, ad esempio, l'esperienza schematizzata nella fig. 1: un fascio di luce polarizzata nella direzione u (di intensità I0) incide sul polarizzatore P orientato lungo la direzione a che fa un angolo ? con la direzione di polarizzazione. Si ottengono due fasci emergenti: uno diretto, di polarizzazione a e di intensità I2 cos2 ?, l'altro deflesso da un lato, di polarizzazione ortogonale e di intensità I0 sen2 ?. In meccanica quantistica si descrive il fascio luminoso come formato di fotoni polarizzati nella direzione u. Una frazione cos2 ? dei fotoni è trasmessa, mentre l'altra, sen2 ?, è riflessa. Se guardiamo al processo come interazione di un singolo fotone, si può dire che esso subisce una misura di polarizzazione secondo a, misura che può dare due risultati: uno (+1) corrispondente alla polarizzazione a con una probabilità cos2 ? di verificarsi; l'altro (-1) corrispondente alla polarizzazione ortogonale ad a con una probabilità sen2 ? di essere ottenuto. Questa natura fondamentalmente statistica delle predizioni quantistiche aveva turbato numerosi fisici, fra i quali Louis de Broglie e Albert Einstein. Per quest'ultimo, una teoria fondamentale deve essere capace di predire con certezza il comportamento di un sistema il cui stato iniziale è determinato. Il ricorso alla probabilità in fisica è un ausilio utile quando è tecnicamente impossibile portare a termine il trattamento esatto del problema. Ciò avviene, per esempio, nella teoria cinetica dei gas di Maxwell, dove la descrizione esatta del movimento di 1023 molecole di un gas è evidentemente esclusa in pratica anche se è concettualmente possibile. Ma una teoria fondamentale non può essere probabilistica, come la celebre frase di Einstein ‟Dio non gioca a dadi" sta a significare, e quindi il carattere probabilistico della teoria quantistica è un'indicazione dell'esistenza di un livello sottostante che permetterebbe una descrizione più dettagliata del mondo fisico. Quindi, la meccanica quantistica non rappresenterebbe altro che una descrizione statistica di fenomeni che avvengono a una scala più piccola: è questa descrizione più completa che si dovrebbe cercare di scoprire.
Secondo l'interpretazione, nota come ‛interpretazione di Copenaghen', della quale Niels Bohr fu il massimo artefice, la meccanica quantistica dà invece in forma probabilistica la descrizione fisica più completa che si possa concepire. L'impossibilità di andare più oltre è dovuta alla quantizzazione di certe quantità che non possono prendere valori arbitrariamente piccoli. La validità di questa posizione è assicurata dall'esistenza delle relazioni di indeterminazione di Heisenberg, sulle quali Einstein ha pertanto concentrato i suoi primi attacchi cercando di contraddirle con diverse esperienze concettuali, compatibili con le leggi fondamentali della fisica ma ben al di là delle possibilità di verifica con le tecnologie di quell'epoca. Su questa prima fase della discussione si devono ricordare i congressi Solvay del 1927 e del 1930, nel corso dei quali Bohr riuscì facilmente a superare le argomentazioni di Einstein.
Sembra che alla fine di queste discussioni Einstein si sia convinto che la teoria quantistica fosse corretta, pur continuando a pensare che fosse incompleta, e da allora tentò di dimostrare direttamente questo suo punto di vista.
b) L'argomento di Einstein, Podolsky e Rosen.
Nel 1935 Einstein e i suoi collaboratori, Boris Podolsky e Nathan Rosen, pubblicarono sulla rivista ‟Physical review" (v. Einstein e altri, 1935) il celebre argomento - in seguito spesso chiamato ‛paradosso EPR' dal nome dei suoi scopritori - che dimostrava l'incompletezza della meccanica quantistica basandosi sulle predizioni che essa stessa formulava.
L'esperienza schematizzata nella fig. 2 presenta una variante della situazione scoperta da Einstein, Podolsky e Rosen ispirata da un suggerimento di David Bohm (v., 1951). La meccanica quantistica predice una correlazione molto stretta fra le misure di polarizzazione di due fotoni ν1 e ν2 lontani ma emessi da una sorgente comune che li ha prodotti in uno stato di polarizzazione definito da:
nella quale ∣x1, x2〉 rappresenta una coppia di fotoni polarizzati secondo l'asse Ox, perpendicolare alla direzione di propagazione, e ∣y1, y2〉 rappresenta una coppia di fotoni polarizzati secondo l'asse Oy perpendicolare a Ox e alla direzione di propagazione. La meccanica quantistica prevede una correlazione totale tra le polarizzazioni dei due fotoni appartenenti a un tale stato, detto ‛stato EPR'. Per esempio per direzioni di misura parallele, un risultato + 1 per ν1 implica con sicurezza un risultato +1 per ν2 (e similmente, se si ottiene - 1 per ν1, con certezza si otterrà - 1 per ν2). Ma secondo Einstein la misura sul fotone ν2 non dovrebbe essere influenzata dalla misura distante su ν1, poiché il principio di causalità relativistico impedisce a un'interazione di propagarsi con velocità maggiore di quella della luce. Perciò il fotone ν2 deve possedere una proprietà che determina il risultato + 1 o - 1 prima che si effettui la misura. Secondo l'espressione di Einstein, Podolsky e Rosen questa proprietà è un ‟elemento di realtà fisica".
Ora, secondo il formalismo quantistico, che non attribuisce alcuna proprietà di questo tipo a ν2, tutte le coppie sono identiche ancorché nel 50% dei casi si ottenga +1 e nel 50% degli altri casi si ottenga - 1. Secondo Einstein e i suoi collaboratori si deve dunque concludere che il formalismo quantistico è incompleto poiché esso non spiega tutti gli elementi della realtà fisica.
c) La separabilità quantistica è il nocciolo della discussione.
Questa volta Bohr non poté confutare gli argomenti di Einstein a livello tecnico, poiché su questo piano il ragionamento di Einstein, Podolsky e Rosen è inattaccabile. La discussione deve dunque spostarsi a livello dei concetti e per tentare di comprendere la risposta di Bohr (v., 1935) occorre, schematizzando alquanto, precisare le ipotesi alla base di quel ragionamento. Ipotesi 1: le predizioni della meccanica quantistica sono giuste; ipotesi 2: nessuna interazione può propagarsi con velocità superiore a quella della luce (causalità relativistica); ipotesi 3: quando due oggetti sono molto lontani l'uno dall'altro è possibile parlare separatamente degli elementi della realtà fisica di ciascuno di essi.
È sull'ipotesi 3 (talvolta chiamata principio di separabilità) che si concentra la confutazione di Bohr, secondo cui non si può parlare in astratto degli elementi di realtà fisica di un sistema; ogni esperienza di fisica comporta un sistema da studiare e un apparecchio di misurazione, ed è soltanto precisando l'insieme dei due che si può parlare di realtà fisica. In conclusione secondo Bohr la nozione di realtà fisica di Einstein, Podolsky e Rosen è priva di senso.
Il nocciolo del dibattito sta dunque nel concetto di realtà fisica separabile. Secondo Einstein il mondo può essere concepito come formato di entità localizzabili nello spazio-tempo dotate di proprietà che costituiscono la loro realtà fisica; tali entità possono interagire localmente in senso relativistico, cioè a dire attraverso interazioni che non si propaghino con velocità superiore a quella della luce. Una tale concezione del mondo è solitamente chiamata ‛realistica locale' o ‛separabile'. Bohr, pur considerandosi un fisico realista, propose una versione differente (e, va detto, meno chiara) di realtà fisica. Rifiutandosi di considerare una realtà fisica indipendente (separata) dallo strumento di misurazione, Bohr poté resistere all'attacco di Einstein, Podolsky e Rosen, ma questa confutazione non riuscì a soddisfare Einstein, tanto che il dibattito fra i due durò fino alla loro morte senza che peraltro si aggiungesse alcun nuovo argomento veramente decisivo.
d) Le reazioni.
L'impatto di questo dibattito sulla comunità scientifica fu assai limitato. Alcuni fisici furono convinti dalle argomentazioni di Einstein, Podolsky e Rosen e cercarono di inventare delle teorie per completare la meccanica quantistica con l'introduzione di un livello sottostante di descrizione (teoria dell'onda pilota di Louis de Broglie, teorie con variabili nascoste di David Bohm e di Jean-Pierre Vigier; v. Jammer, 1974). Tuttavia, la grande maggioranza dei fisici seguì Bohr, sia perché erano stati convinti dalla sua risposta, sia, più probabilmente, perché avevano fiducia in lui senza tuttavia preoccuparsi di approfondire il problema. Questa fiducia era rinforzata dal ‛teorema di von Neumann', enunciato nel 1932 nel libro in cui erano poste le basi matematiche della meccanica quantistica. In questo libro von Neumann (v., 1932) aveva affrontato il problema dell'interpretazione del carattere statistico delle predizioni quantistiche nei termini delle variabili nascoste e aveva ‛dimostrato' l'incompatibilità delle proprietà matematiche del formalismo quantistico con l'esistenza di un formalismo sottostante nel quale intervenissero delle ‛variabili nascoste'.
Per comprendere la debole reazione all'argomento di Einstein, Podolsky e Rosen da parte della maggioranza dei fisici bisogna tenere presente l'enorme messe di successi della meccanica quantistica in tutti i campi, dalla fisica dei solidi alla chimica, passando per la teoria quantistica della radiazione. Per di più, poiché tutti erano d'accordo sul modo di utilizzare in pratica la teoria quantistica, la scelta fra l'una o l'altra posizione non aveva conseguenze pratiche sulla ricerca, cosicché il problema sembrava limitarsi a una questione di interpretazione o sconfinare addirittura nella filosofia.
È comprensibile perciò l'interesse sollevato dalle ricerche di John Bell, il quale nel 1964 fece passare il dibattito dal terreno delle idee a quello dell'esperimento.
2. Il teorema di Bell
a) Un passo avanti concettuale.
Il primo contributo di Bell ai fondamenti concettuali della meccanica quantistica fu la dimostrazione, nel 1964, dell'inesattezza del teorema di von Neumann (v. Bell, 1964). Egli osservò innanzitutto che l'esistenza di teorie con variabili nascoste come quella di Bohm rappresentava un controesempio al teorema. Inoltre egli identificò un'ipotesi apparentemente ovvia, seppure non verificata, che minava tutta la dimostrazione. A questo punto egli era pronto a riprendere il programma di Einstein, Podolsky e Rosen, ciò che fece nel 1966 in un secondo articolo che rimase celebre (v. Bell, 1966).
In questo articolo, Bell estende l'argomento di Einstein, Podolsky e Rosen esaminando le possibili conseguenze della conclusione secondo la quale la meccanica quantistica sarebbe incompleta. Egli completò quindi la teoria introducendo delle ‛variabili nascoste' per interpretare le correlazioni di Einstein, Podolsky e Rosen. Si tratta di proprietà suscettibili di variare da una coppia (per esempio di fotoni) all'altra ma comuni ai due membri di una stessa coppia. I risultati delle misure di polarizzazione dipendono da questa proprietà comune, cosicché si capisce che le misure effettuate sui due membri di una stessa coppia possono essere correlate.
Fedele allo spirito dell'articolo di Einstein, Podolsky e Rosen, Bell impose inoltre al suo formalismo una condizione di località strettamente legata alle ipotesi 2 e 3 elencate più sopra. Ciò fatto dimostrò che una tale teoria (teoria separabile con variabili nascoste) è in conflitto con la meccanica quantistica. La grande forza del ragionamento di Bell sta nella sua generalità. Esso non è ristretto a una teoria particolare con variabili nascoste, ma si applica a tutte le teorie separabili con variabili nascoste le cui predizioni soddisfino certe ineguaglianze (ineguaglianze di Bell), mentre le predizioni della meccanica quantistica le violano.
Il dibattito cambiò dunque di natura. Prima si poteva adottare la posizione di Bohr o quella di Einstein pur continuando a credere all'esattezza delle predizioni quantistiche per le correlazioni di Einstein, Podolsky e Rosen. Con la teoria di Bell, invece, si stabilisce che, se la posizione di Einstein è corretta, le correlazioni di Einstein, Podolsky e Rosen violano le predizioni quantistiche. Il conflitto è divenuto quindi di ordine quantitativo e il dibattito è ritornato nel dominio della fisica, poiché è sufficiente - in linea di principio - eseguire la misurazione corrispondente per decidere la questione.
b) Le ineguaglianze di Bell e il conflitto con la meccanica quantistica.
Benché sia estremamente efficace, il teorema di Bell può essere dimostrato senza grandi difficoltà. Il punto di partenza è quello di trovare un formalismo in cui appaiano le variabili nascoste λ che caratterizzano ciascuna coppia, la loro densità di probabilità ρ (λ) e delle funzioni A (λ, a) e B (λ, b) con valori +1 o - 1 che rappresentino il risultato della misura di polarizzazione. Questo formalismo permette di esprimere il coefficiente di correlazione delle misure di polarizzazione quando i polarizzatori sono orientati lungo le direzioni a e b:
E (a, b) = ∫ A (λ, a) B (λ, b) ρ (λ) dλ. (2)
La condizione di località di Bell è espressa qui dalla proprietà che la risposta A (λ, a) del primo polarizzatore non dipenda dall'orientamento b dell'altro polarizzatore (e viceversa), o dalla proprietà che la densità di probabilità ρ (λ) che caratterizza la sorgente non dipenda dagli orientamenti a e b dei polarizzatori.
L'espressione (2) è sufficiente a dimostrare le ineguaglianze di Bell (nella forma data loro da Clauser, Horn, Shimony e Holt: v. Clauser e Shimony, 1978).
Consideriamo la quantità S, definita da:
S = E (a, b) - E (a, b′) + E (a′, b) + E (a′, b′), (3)
nella quale compaiono i coefficienti di correlazione della polarizzazione corrispondenti agli orientamenti a e a′ per il primo polarizzatore e b e b′ per il secondo. Essa può assumere solo i valori:
-2 ≤ S ≤ 2. (4)
Per dimostrare tale ineguaglianza consideriamo la quantità
s = α (β - β′) + α′(β + β′), (5)
nella quale ciascuno dei quattro numeri α, β, α′ e β′ vale ± 1. Si verifica immediatamente che s vale + 2 o - 2. Ora la quantità S dell'equazione (3) è la media - pesata con ρ (λ) - di numeri di tipo (5), che cioè valgono o 2 o - 2. Questa media è perciò compresa fra 2 e - 2, cosicché si ottiene l'ineguaglianza di Bell (4).
Consideriamo ora i risultati di un calcolo quantistico per una situazione del tipo Einstein-Podolsky-Rosen, per esempio per una coppia di fotoni prodotti nella cascata radiativa della fig. 3. È facile dimostrare che il coefficiente di correlazione delle polarizzazioni vale:
EMQ (a, b) = cos [2 (a, b)], (6)
essendo (a, b) l'angolo fra le direzioni a e b dei due polarizzatori. Utilizziamo ora questo risultato per calcolare la quantità S prevista dal calcolo quantistico nel caso delle orientazioni della fig. 4: il risultato, quando l'angolo tra i polarizzatori è uguale e pari a 22,5 gradi, è:
SMQ (22,5o) = 2 √2 ≅ 2,83; (7)
tale risultato viola manifestamente l'ineguaglianza (4). Esistono dunque delle situazioni in cui le teorie separabili a variabili nascoste e la meccanica quantistica conducono a previsioni diverse, e proprio questo dato di fatto determina l'incompatibilità di tali teorie.
Quando due approcci teorici conducono a predizioni quantitative diverse, è necessario determinare sperimentalmente qual è quello più attendibile.
3. Il passaggio all'esperienza
a) Situazioni eccezionali.
Dato l'immenso successo della meccanica quantistica si sarebbe potuto credere a priori di disporre già nel 1965 di numerosi risultati sperimentali che violassero l'ineguaglianza di Bell, ma in effetti si constatò rapidamente che nessun risultato era stato ottenuto in una situazione ‛opportuna' (tale cioè che le predizioni quantistiche violassero le ineguaglianze di Bell). Invero, le situazioni in cui può esistere un conflitto sono molto rare. Per di più, in un'esperienza reale le imperfezioni inevitabili riducono le correlazioni previste dalla meccanica quantistica, e ciò attenua o addirittura fa sparire il conflitto nelle situazioni in cui esso in linea di principio può esistere. È stato quindi necessario concepire degli esperimenti progettati in maniera tale da poter verificare le ineguaglianze di Bell.
b) Esperienze di prima generazione.
I primissimi esperimenti (v. Pipkin, 1978; v. Clauser e Shimony, 1978), che utilizzavano coppie di fotoni γ prodotti dalla disintegrazione del positronio, sono di facile interpretazione. Dato che non esiste polarizzatore efficace per fotoni di questa energia (0,5 MeV), è necessario passare attraverso misure e ragionamenti molto indiretti. Un'esperienza che utilizzava protoni presenta problemi analoghi.
Le coppie di fotoni visibili emessi in cascate radiative atomiche ben scelte rappresentano candidati molto più idonei, poiché esistono eccellenti polarizzatori per la luce. I primi esperimenti di questo tipo (compiuti da R. Holt e F. Pipkin a Harvard, e da J. Clauser e R. Friedman a Berkeley) diedero risultati contraddittori, il che non è troppo strano considerando l'estrema debolezza dei segnali ottenuti. Grazie all'utilizzazione di un laser, Fry e Thompson poterono ottenere nel 1986 un risultato assai più attendibile in favore della meccanica quantistica. L'esperienza restava nondimeno molto lontana dallo schema ideale della fig. 2, poiché i polarizzatori utilizzati non consentivano che un solo risultato della misura sui due possibili: il confronto con l'ineguaglianza di Bell restava ancora indiretto.
c) Risultati incontestabili.
Una seconda generazione di esperimenti, realizzati all'Institut d'Optique d'Orsay (Université Paris-sud) da Alain Aspect, Philippe Grangier, Gerard Roger e Jean Dalibard, è stata resa possibile grazie alla preparazione di una nuova sorgente di coppie di fotoni correlati, allo stesso tempo intensa e molto pura (v. fig. 3). In questa figura sono rappresentati tre livelli energetici, f, r, e, di un atomo. Per una scelta opportuna del sistema, l'atomo portato al livello e si diseccita emettendo in successione due fotoni ν1 e ν2 che presentano correlazioni del tipo Einstein-Podolsky-Rosen. Nelle esperienze di Orsay una sorgente pura e intensa di coppie di fotoni Einstein-Podolsky-Rosen è stata ottenuta eccitando direttamente la transizione f → e tramite un processo non lineare a due fotoni ν′ e ν″. Una tale eccitazione è stata possibile grazie allo sviluppo di laser accordabili molto stabili. Tale sorgente ha consentito di ottenere, in un'esperienza della durata di un minuto, una precisione di misura (1%) che nelle esperienze precedenti richiedeva molte ore. Associata a componenti ottiche vicine alla perfezione, questa sorgente ha anzitutto dato una conferma molto netta dei risultati precedenti a favore della meccanica quantistica, con una precisione statistica migliorata. Inoltre essa ha permesso di chiudere il dibattito sulla possibilità della sparizione della correlazione quantistica (6) quando i polarizzatori erano sufficientemente lontani dalla sorgente. In effetti, anche utilizzando polarizzatori posti a 6 m di distanza dalla sorgente, che è superiore alla lunghezza di coerenza dei fotoni emessi nella cascata radiativa della fig. 3, le misure hanno dato risultati compatibili con le previsioni quantistiche e incompatibili con le ineguaglianze di Bell corrispondenti a questa situazione (v. Aspect e altri, 1981).
L'uso di veri analizzatori di polarizzazione capaci di misurare i due risultati possibili ha poi permesso di compiere la prima esperienza che riproduceva esattamente lo schema ideale della fig. 2, e quindi di verificare direttamente le ineguaglianze di Bell (v. Aspect e altri, Experimental realization..., 1982). Per l'orientazione della fig. 4 si è ottenuto:
S = 2,697 ± 0,015, (8)
un risultato che viola incontestabilmente l'ineguaglianza (4). Inoltre tutte le misure sono in eccellente accordo con le previsioni quantistiche che tengono conto delle piccole imperfezioni dell'apparecchio. Per la sua precisione e la semplicità concettuale dello schema utilizzato, questa esperienza rappresenta una conferma particolarmente probante delle previsioni quantistiche in una situazione ‛sensibile' Einstein-Podolsky-Rosen.
d) Esperimenti con polarizzatori variabili.
Nel suo articolo iniziale Bell aveva insistito sulla necessità di una condizione di località per arrivare a un conflitto con la meccanica quantistica. Questa condizione del tutto naturale esclude qualunque interazione diretta fra i polarizzatori o fra i polarizzatori e la sorgente. Nel formalismo di Bell, esposto più sopra, questa condizione si traduce, come abbiamo visto, nella proprietà per cui la risposta A (λ, a) del primo polarizzatore non dipende dall'orientazione b dell'altro polarizzatore (e viceversa), oppure in quella per cui la densità di probabilità ρ (λ) che caratterizza l'emissione di coppie dalla sorgente non dipende dalle orientazioni a e b dei polarizzatori.
Pur essendo molto naturale, questa condizione non può essere dimostrata con gli schemi sperimentali precedenti e deve essere ammessa come ipotesi. Al contrario, in un'esperienza nella quale le direzioni dei polarizzatori siano modificate molto rapidamente e in maniera aleatoria, la possibilità di un'interazione diretta fra polarizzatori o di un'influenza dei polarizzatori sulla sorgente è esclusa dal principio di causalità relativistica (ipotesi 3). È in gioco allora il principio di separabilità nella sua globalità (ipotesi 2 e 3).
Per realizzare delle oscillazioni rapide il gruppo di Orsay (v. Aspect e altri, Experimental tests..., 1982) ha sostituito ciascun polarizzatore rappresentato nella fig. 2 con uno scambio ottico seguito da due polarizzatori con orientazioni diverse (v. fig. 5). Lo scambio C1 invia alternativamente la luce verso i polarizzatori PI o PI′ con orientazioni a e a′. L'insieme è equivalente a un polarizzatore unico orientato secondo a e a′. Lo scambio C2 seguito dai polarizzatori PII e PII′ compie una funzione analoga. In questa esperienza l'intervallo di tempo fra due scambi era dell'ordine di 10 ns, che è più breve del tempo di propagazione della luce fra le due estremità dell'apparecchio, lungo 12 m (40 ns). Questo esperimento è meno probativo di quanto si sarebbe potuto sperare a causa delle difficoltà tecniche legate all'introduzione degli ‛spillaggi' ottici. Esso ha tuttavia fornito risultati in buon accordo con la meccanica quantistica che violano nettamente le ineguaglianze di Bell (per 5 deviazioni standard).
Si può dunque concludere che la sola esperienza che incorpora dei polarizzatori variabili è anch'essa in favore della meccanica quantistica, sebbene il livello di certezza dei dati così ottenuti sia meno elevato rispetto a quello dei dati ricavati dalla migliore esperienza statica. Sarebbe certamente utile controllare questo risultato per mezzo di esperimenti analoghi migliorati.
e) Una nuova generazione di esperimenti.
Gli esperimenti discussi più sopra non sono perfetti a causa della scarsa efficienza globale di rivelazione dei fotoni: i fotoni emessi dalla sorgente sfuggono, nella grande maggioranza, ai rivelatori. Le misurazioni effettuate sono ciò nondimeno valide se si suppone che il sottoinsieme dei fotoni effettivamente rivelati fornisca un campione non ‛influenzato', in senso statistico, dell'insieme dei fotoni emessi. Questa ipotesi è del tutto naturale poiché i processi che conducono alla non rivelazione dei fotoni non sono legati alla loro polarizzazione. Tuttavia sarebbe preferibile dal punto di vista logico evitare di dover fare questa ipotesi supplementare (rispetto alle ipotesi di Bell): ciò in linea di principio è possibile a condizione di rivelare tutte le coppie emesse.
Il primo miglioramento da apportare a questi esperimenti sarebbe dunque quello di utilizzare rivelatori di maggior efficienza, il che è possibile grazie ai continui progressi tecnologici nel campo dei rivelatori. Si potrebbe allora pensare a un esperimento ideale a condizione che le direzioni di emissione dei fotoni della coppia siano perfettamente correlate. Ora questo non può avvenire nelle esperienze che utilizzano una cascata radiativa, poiché l'atomo nello stato finale è libero e può rinculare in una direzione qualsiasi. Esiste però un altro processo di emissione di coppie di fotoni, chiamato ‛fluorescenza parametrica', che soddisfa questa condizione di correlazione angolare: si tratta di un processo non lineare che si produce in un materiale cristallino e che genera due fotoni correlati per ‛divisione' di un fotone incidente. La condizione ‛di accordo di fase', ben nota in ottica non lineare, assicura allora la correlazione delle direzioni di emissione (v. fig. 6).
Da circa dieci anni questo processo è stato oggetto di intenso studio (v. Rarity e Tapster, 1990) in quanto renderebbe possibile effettuare delle verifiche delle ineguaglianze di Bell utilizzando grandezze fisiche diverse dalla polarizzazione (per esempio, l'energia o l'impulso dei fotoni). È importante notare che il formalismo quantistico si applica in maniera simile in situazioni apparentemente molto diverse: la violazione delle ineguaglianze di Bell appare sempre come un effetto di interferenze ‛non locali' fra ampiezze di probabilità.
Molti esperimenti di questo tipo sono stati realizzati e hanno in generale condotto a un buon accordo con la meccanica quantistica e a una violazione netta delle ineguaglianze di Bell dell'ordine di una decina di scarti tipici nelle migliori esperienze. John Rarity e Paul Tapster, autori di questo esperimento in Gran Bretagna, sono anche riusciti a inviare ciascun fotone in una fibra ottica, riuscendo in tal modo a verificare le ineguaglianze di Bell su distanze fino a 4 km.
Va tuttavia notato che, nonostante gli sforzi concentrati in questo esperimento, le difficoltà tecniche rendono molto bassa l'efficienza di rivelazione e le verifiche realizzate agli inizi degli anni ottanta per mezzo di cascate radiative restano, a distanza di oltre 10 anni, le migliori in termini di rapporto segnale/rumore. Questa situazione potrebbe cambiare, poiché parecchi gruppi hanno iniziato nel 1993 esperimenti volti a ottenere un'efficienza di rivelazione superiore al 90%: il gruppo di R. Chiao a Berkeley si propone di usare delle coppie di fotoni parametrici (v. Kwiat e altri, 1994), mentre quello di E. Fry nel Texas lavora su atomi di mercurio ottenuti per fotodissociazione di molecole (v. Fry e altri, 1995).
4. Conclusione
A parte alcune riserve, le esperienze effettuate hanno dato risultati in favore della meccanica quantistica, che, grazie al teorema di Bell, hanno un significato molto vasto: è impossibile interpretare questi esperimenti per mezzo di teorie locali o separabili a variabili nascoste e pertanto non vi è alcuna speranza di completare in questa direzione la meccanica quantistica.
Occorre dunque rinunciare a una certa concezione del mondo fisico nello spirito delle ipotesi 2 e 3 del ragionamento di Einstein, Podolsky e Rosen, concezione chiamata separabile o ‛realistica locale'. È in questo senso che si debbono intendere le affermazioni secondo le quali la meccanica quantistica sarebbe non separabile: non si può conservare allo stesso tempo la località e una descrizione quasi classica della realtà fisica. Non si deve tuttavia concludere che sia possibile trasmettere informazione utilizzabile violando il principio di causalità relativistica (con velocità superiore a quella della luce).
Si è voluto talvolta vedere nella violazione delle ineguaglianze di Bell la prova che nel suo dibattito con Bohr era Einstein ad aver torto. Ciò è certamente ingiusto, non foss'altro perché Einstein, che è morto prima della dimostrazione del teorema di Bell, non conosceva l'incompatibilità della sua posizione con le predizioni della meccanica quantistica. Egli ha avuto l'immenso merito di scoprire una situazione in cui le predizioni quantistiche appaiono straordinarie se ci si attiene alle interpretazioni di Copenaghen. Va dato naturalmente a Niels Bohr il merito di aver immediatamente compreso la portata del ragionamento di Einstein, Podolsky e Rosen e di aver capito che questo non conduceva di per sé all'incoerenza della teoria quantistica. Infine è a Bell che si deve il merito di aver chiarito il problema in modo da permettere di dimostrare sperimentalmente che la natura ha veramente le proprietà straordinarie di non separabilità predette dalla meccanica quantistica.
BIBLIOGRAFIA
Aspect, A., Experimental tests of Bell's inequalities in atomic physics, in Atomic physics 8 (a cura di I. Lindgren, A. Rosen e S. Svanberg), New York 1983, pp. 103-128.
Aspect, A., Dalibard, J., Roger, G., Experimental test of Bell's inequalities using time-varying analyzers, in ‟Physical review letters", 1982, IL, pp. 1804-1807.
Aspect, A., Grangier, P., Roger, G., Experimental tests of realistic local theories via Bell's theorem, in ‟Physical review letters", 1981, XLVII, pp. 460-463.
Aspect, A., Grangier, P., Roger, G., Experimental realization of Einstein-Podolsky-Rosen-Bohm Gedankenexperiment: a new violation of Bell's inequalities, in ‟Physical review letters", 1982, IL, pp. 91-94.
Bell, J. S., On the Einstein-Podolsky-Rosen paradox, in ‟Physics", 1964, I, pp. 195-200.
Bell, J. S., On the problem of hidden variables in quantum mechanics, in ‟Reviews of modern physics", 1966, XXXVIII, pp. 447-452.
Bell, J. S., Speakable and unspeakable in quantum mechanics, Cambridge 1987.
Bohm, D., Quantum theory, New York 1951.
Bohr, N., Can quantum-mechanical description of physical reality be considered complete?, in ‟Physical review", 1935, XLVIII, pp. 696-702.
Bohr, N., Discussion with Albert Einstein on epistemological problems in atomic physics, in Albert Einstein, philosopher-scientist (a cura di P. A. Schilpp), Evanston, Ill., 1949, pp. 201-241 (tr. it.: Discussione con Einstein sui problemi epistemologici della fisica atomica, in Albert Einstein, scienziato e filosofo, Torino 1958, pp. 147-190).
Clauser, J. F., Shimony, A., Bell's theorem: experimental tests and implications, in ‟Reports on progress in physics", 1978, XLI, pp. 1881-1927.
Einstein, A., Podolsky, B., Rosen, N., Can quantum-mechanical description of physical reality be considered complete?, in ‟Physical review", 1935, XLVII, pp. 770-780.
Espagnat, B. d', À la recherche du réel, Paris 1979 (tr. it.: Alla ricerca del reale, Torino 1983).
Fry, E. S., Walther, T., Li, S., Proposal for a loophole-free test of the Bell inequalities, in ‟Phisical review. A", 1995, LII, pp. 4381-4395.
Jammer, M., The philosophy of quantum mechanics, New York 1974.
Kwiat, P. G., Eberhardt, P. H., Steinberg, A. M., Chiao, R. Y., A proposal for a loophole-free Bell inequality experiment, in ‟Physical review. A", 1994, IL, pp. 3209-3220.
Neumann, J. von, Mathematische Grundlagen der Quantenmechanik, Berlin 1932.
Pipkin, F. M., Atomic physics tests of the basic concepts in quantum mechanics, in Advances in atomic and molecular physics (a cura di D. R. Bates e B. Bederson), London 1978, pp. 281-340.
Rarity, J. G., Tapster, P. R., Experimental violation of Bell's inequalities based on phase and momentum, in ‟Physical review letters", 1990, LXIV, pp. 2495-2498.