MECCANICA QUANTISTICA

Meccanica quantistica

La meccanica quantistica può essere considerata la più efficiente descrizione della natura elaborata dall’uomo. I suoi successi sono stati evidenti fin dalla sua introduzione, all’inizio del 20° sec., e ancora oggi la sua validità non è stata contraddetta da alcun esperimento. Essa consiste nell’introduzione di un apparato matematico che consente di descrivere, in maniera quantitativa estremamente accurata, gran parte della realtà sensibile. Rispetto alla meccanica e all’elettromagnetismo classici, i suoi postulati (quali, per es., l’assioma secondo cui la massima conoscenza possibile di un sistema è contenuta in una funzione d’onda invece che nei valori delle grandezze caratterizzanti il sistema) appaiono profondamente non intuitivi, al punto da implicare un drastico cambio della visione della realtà. Le prime analisi concettuali delle implicazioni di tali postulati hanno condotto alla formulazione di un metodo pragmatico, secondo il quale la meccanica quantistica andava utilizzata essenzialmente come teoria predittiva per il mondo microscopico. I suoi continui e sempre più convincenti successi in tutti gli ambiti della fisica microscopica, dalla chimica alla fisica nucleare, hanno indicato come la validità dei suoi postulati, apparentemente paradossali, sia di natura talmente generale da suggerirci di usarli anche come paradigmi per lo sviluppo di apparati e tecnologie che sarebbero impossibili in una realtà classica. In altri termini, la chiave di lettura dei più recenti sviluppi nella meccanica quantistica consiste, più che nella sua accertata capacità predittiva, nell’utilizzo delle sue ‘stranezze’ al fine di realizzare funzioni pratiche. In tal senso, questi sviluppi sono volti alla creazione di una tecnologia la cui natura concettuale è del tutto nuova (quantum technology).

In questo ambito, notevole attenzione è stata rivolta all’utilizzo di quegli aspetti della meccanica quantistica che offrono la possibilità di superare alcuni limiti, tradizionalmente assunti come concettualmente invalicabili, della tecnologia e delle macchine. Alcuni esempi di tali limiti: l’impossibilità per un singolo componente di una macchina di svolgere più funzioni contemporaneamente, superabile mediante la computazione quantistica; l’impossibilità di violare il concetto di località, superabile, per es., mediante schemi di teletrasporto; l’impossibilità di creare un codice inattaccabile, superabile nell’ambito del possibile futuro sviluppo della crittografia quantistica; l’impossibilità per un oggetto macroscopico di manifestare caratteristiche ondulatorie, superabile, per es., a temperature molto basse, mediante schemi tipici della cosiddetta condensazione di Bose-Einstein.

Come ogni teoria fisica, la meccanica quantistica si basa su una descrizione quantitativa dei fenomeni fisici tramite l’introduzione di una procedura di misura che consente di associare, in maniera univoca, un numero reale ad alcune caratteristiche del sistema in esame, in ciascun punto dello spazio e del tempo (considerati concetti innati). Tali caratteristiche, le grandezze fisiche o ‘osservabili’, costituiscono l’unico contatto obiettivo con la realtà sensibile. Concettualmente, ha senso chiedersi cosa avvenga di una grandezza fisica quando non è soggetta a misurazione. A tale proposito, nella visione classica del mondo il valore della grandezza è considerato presente in maniera univoca a ogni istante al di fuori dell’osservatore, ovvero indipendentemente dal fatto che la misurazione sia effettivamente eseguita. Al contrario, la meccanica quantistica nega questo assunto, e contempla l’eventualità che, quando non osservata, la grandezza possa assumere qualunque valore consentito dalla sua definizione. Quale valore essa in effetti assuma all’atto della misurazione è una domanda a cui si può rispondere solo in modo statistico, nel senso che le leggi della meccanica quantistica sono in grado di prevedere solo la probabilità con cui un dato valore può essere ottenuto a un dato istante. Così si esprime uno dei padri fondatori della meccanica quantistica, Niels Bohr: «A rigore, il formalismo matematico della teoria quanti;stica [...] offre semplicemente le regole di calcolo per la derivazione dei valori medi di osservazioni compiute in condizioni sperimentali ben definite, specificate tramite concetti di fisica classica» (The philosophical writings of Niels Bohr, 3° vol., Essays 1958-1962 on atomic physics and human knowledge, 1963, p. 60).

La differenza fra la visione classica e quella quantistica del mondo è resa esplicita nella descrizione del più fondamentale dei fenomeni, il moto dei corpi. Nel limite classico, il moto è regolato dalle leggi di Newton, secondo le quali la posizione di una particella può essere prevista con assoluta certezza a ogni istante successivo rispetto a una singola misura di posizione e velocità, anche se nessun’altra misurazione è stata o verrà in effetti eseguita. Viceversa, in meccanica quantistica, le leggi di Newton sono essenzialmente sostituite dall’equazione di Schrödinger, la quale, invece di determinare la traiettoria del corpo nello spazio e nel tempo, ne descrive in maniera olistica lo stato tramite la funzione d’onda, una funzione complessa ψ dello spazio e del tempo il cui modulo quadrato rappresenta la densità di probabilità che la particella occupi a un dato istante una data posizione, qualora tale misura venga in effetti eseguita. In altri termini, la funzione d’onda non rappresenta una grandezza fisica, ma la sua evoluzione temporale permette di determinare la probabilità che ogni grandezza fisica assuma uno dei suoi possibili valori. È bene sottolineare come tale evoluzione sia di natura completamente deterministica, e come l’interpretazione statistica sia necessaria solo all’atto della misurazione, il cui risultato non è a priori prevedibile. Si noti inoltre come il ruolo giocato dallo spazio e dal tempo nella meccanica quantistica non sia sostanzialmente diverso da quello della fisica classica, essendo in definitiva entrambe le grandezze parametri la cui conoscenza è supposta a priori.

È sorprendente come una teoria, che è stata in grado di interpretare fatti assolutamente inspiegabili prima del suo apparire (quali, per es., la radiazione di corpo nero o gli spettri atomici), che ha ricevuto un ammontare notevolissimo di evidenze sperimentali tra le più precise mai ottenute nella storia della fisica, e che ha dato luogo a uno straordinario sviluppo della moderna tecnologia (dalla fissione alla fusione nucleare, dai semiconduttori ai laser, dalla superconduttività alla risonanza magnetica nucleare), non sia stata ancora codificata in maniera permanente e susciti tuttora dubbi sull’interpretazione da dare alla teoria stessa e sulla sua consistenza interna. A cominciare da quelli epistemologici sollevati nel 1935 dal famoso paradosso EPR (Einstein-Podolsky-Rosen), tali dubbi rappresentano una sorta di riflessione critica del pensiero scientifico, e contribuiscono all’approfondimento dell’interpretazione della teoria. Ciò a sua volta conduce sia a una migliore comprensione della stessa (non località, variabili nascoste, stati entangled, teoria della misura ecc.), sia a nuove potenziali applicazioni (teletrasporto, crittografia quantistica, computazione quantistica ecc.).

Dopo gli anni ‘eroici’, all’inizio del 20° sec., della meccanica quantistica di Max Planck e di Bohr, la disciplina si è andata evolvendo, ed è stata codificata nell’ambito della cosiddetta interpretazione di Copenaghen, grazie all’opera di grandi scienziati tra i quali Werner K. Heisenberg, Max Born ed Erwin Schrödinger, in una teoria dal grandissimo potere predittivo, culminata nell’applicazione della stessa ai fenomeni elettromagnetici (elettrodinamica quantistica). Come osservato, la sostanza di questa interpretazione è che la funzione d’onda non è di per sé un elemento di realtà, ovvero che a essa non va associato alcun attributo sensibile, ma ha la sola proprietà di consentire la predizione della probabilità che all’atto della misura si ottenga un determinato valore di una grandezza fisica.

Il problema cruciale della teoria è associato alla misura della grandezza fisica in questione. Citiamo ancora Bohr: «La caratteristica essenzialmente nuova nell’analisi dei fenomeni quantistici […] è l’introduzione di una distinzione fondamentale tra l’apparato di misura e gli oggetti da investigare. Ciò è una conseguenza diretta della necessità di tener conto delle funzioni dello strumento di misura in termini puramente classici, escludendo in principio ogni considerazione del quanto di azione» (pp. 3-4). La questione è strettamente legata alla descrizione dell’interazione di un apparato di misura necessariamente macroscopico (cioè leggibile da un essere umano) con l’oggetto microscopico (ossia tale da richiedere una descrizione quantistica) soggetto alla misurazione, e quindi alla susseguente decodifica dell’informazione immagazzinata nel sistema quantistico, ovvero alla sua conversione in un segnale classico leggibile dall’apparato di misura. Comunque, sia che ciò debba essere accettato come un postulato (collasso della funzione d’onda), sia che possa essere in qualche modo giustificato nell’ambito della teoria stessa (decoerenza), il fatto maggiormente in contrasto con la visione del mondo per noi più intuitiva è che l’effetto di una misurazione sia quello di indurre una transizione da diversi valori potenziali a uno specifico valore attuale. Tale caratteristica della natura è oggetto degli sviluppi più recenti della meccanica quantistica, nel senso che essa viene sfruttata nell’elaborazione di algoritmi e processi che sarebbero impossibili in una realtà classica, insieme di predizioni che costituiscono la già citata tecnologia quantistica.

Nel seguito, dopo avere accennato agli aspetti della meccanica quantistica più rilevanti per i recenti sviluppi, verrà effettuata una breve descrizione concettuale delle cosiddette macchine o algoritmi quantistici.

Aspetti fondamentali

I quanti e il principio di indeterminazione

La meccanica quantistica ha permesso il superamento della profonda crisi della fisica classica, ovvero della descrizione dell’Universo tramite le leggi di Newton, applicate fondamentalmente ai fenomeni meccanici, gravitazionali ed elettromagnetici. Nell’ambito classico, lo sviluppo della termodinamica e la sintesi dei fenomeni elettromagnetici contenuta nelle equazioni di Maxwell apparivano come la conclusione di un apparato descrittivo completo dei fenomeni fisici. Nuove evidenze sperimentali alla fine del 19° sec., quali, per es., lo spettro della radiazione di corpo nero, l’effetto fotoelettrico, e le righe di emissione e assorbimento nella spettroscopia atomica, non trovavano ragionevole interpretazione nelle teorie fisiche esistenti. Il primo passo è stato l’introduzione di una nuova costante fondamentale, la costante di Planck h. In effetti, i risultati delle osservazioni relative ai fenomeni di interazione tra la materia e la radiazione elettromagnetica risultano in accordo con l’ipotesi che lo scambio di energia possa avvenire solo in pacchetti, o quanti, di valore hν, dove ν è la frequenza della radiazione. Nulla di simile è previsto nella meccanica classica, dove l’energia scambiata può assumere a priori qualsiasi valore. Questa discretizzazione dell’energia trova una collocazione concettuale compiuta nel principio di indeterminazione di Heisenberg. Tale principio ipotizza l’esistenza, nell’ambito delle grandezze fisiche, di coppie di grandezze, quali per es. la posizione e la quantità di moto di una particella, che non possono essere simultaneamente note con precisione arbitraria, a prescindere dalla raffinatezza delle tecniche di misurazione. Più precisamente, esiste un limite inferiore naturale, dell’ordine della costante di Planck h, del prodotto tra le incertezze delle due grandezze in esame. Per rendere plausibile tale principio, Heisenberg si basa sul fatto che, a causa della suddetta natura a quanti (fotoni) della radiazione, osservare un elettrone per misurarne posizione e quantità di moto implica al minimo l’interazione con un fotone, il quanto di energia elettromagnetica hν. A sua volta, ciò comporta l’impossibilità di misurare contemporaneamente, con precisione arbitraria, la posizione e la quantità di moto, come evidenziato da un semplice esperimento concettuale basato sul cosiddetto microscopio di Heisenberg.

Comportamento ondulatorio e corpuscolare della natura

In regime macroscopico, i fenomeni naturali si possono usualmente distinguere in corpuscolari e ondulatori. Un sasso che cade rappresenta un fenomeno corpuscolare, mentre la perturbazione da esso prodotta nell’acqua di uno stagno ha caratteristiche ondulatorie. Tale distinzione, fondamentale nella fisica macroscopica, non trova fondamento in meccanica quantistica. Uno stesso sistema fisico può manifestare comportamenti ascrivibili talvolta a un’ipotetica natura corpuscolare e talaltra a una ondulatoria. Per es., se inviamo luce su un foro sufficientemente piccolo, osserviamo su uno schermo fotosensibile posto dopo il foro un’immagine complessiva tipica di un fenomeno ondulatorio di diffrazione. Tuttavia, analizzando i dettagli del processo di formazione della figura, notiamo che la distribuzione dell’intensità luminosa, anziché avere una dipendenza regolare dalla posizione e dal tempo, presenta caratteristiche di discontinuità tipiche di una natura corpuscolare. Analogamente, se inviamo un opportuno fascio di elettroni su un cristallo, e osserviamo la distribuzione spaziale degli elettroni diffusi su uno schermo sensibile, notiamo una figura di nuovo ascrivibile a un fenomeno di diffrazione, caratteristico di un’onda. Viceversa, analizzando i singoli eventi di rivelazione, si osserva l’usuale natura corpuscolare degli elettroni stessi. La componente corpuscolare della luce e, rispettivamente, la componente ondulatoria degli elettroni non trovano alcuna interpretazione nell’ambito della fisica classica.

In termini di grandezze fisiche, a un’onda può essere attribuita una lunghezza d’onda λ, mentre lo stato dinamico di un corpo può essere caratterizzato dalla sua quantità di moto p. In realtà, la presenza della costante di Planck h come quantità intrinsecamente associata ai sistemi microscopici suggerisce che essi possano essere caratterizzati simultaneamente da λ e p, tramite l’equazione λ=h/p. Tale relazione, detta per i corpi dotati di massa relazione di de Broglie, consente di legare gli aspetti ondulatorio e corpuscolare della materia e di interpretare quantitativamente i suddetti esperimenti di diffrazione elettronica. È notevole come la diffrazione sia stata recentemente osservata anche per gli atomi, la cui massa è migliaia di volte maggiore rispetto a quella degli elettroni, aprendo la strada a un campo che può essere definito ottica atomica.

figura 1

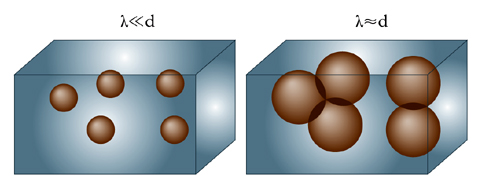
La relazione di de Broglie ha valore universale, ma per corpi macroscopici la quantità di moto p è talmente grande che la lunghezza d’onda risulta così piccola da non dar luogo, nella quasi totalità dei casi, a effetti osservabili. Tuttavia, è stato recentemente possibile osservare fenomeni di natura ondulatoria della materia in sistemi composti da un grande numero di atomi (dell’ordine di 108), sistemi che a tutti gli effetti possono essere considerati macroscopici, tramite la condensazione di Bose-Einstein. Questa condensazione è basata sul fatto che alcuni tipi di atomi, gli atomi bosonici, possono occupare lo stesso stato quantico contemporaneamente, e che, al disotto di una determinata temperatura critica dipendente dalla massa degli atomi e dalla loro densità, una frazione notevole di essi occupa uno stesso stato quantico, lo stato a energia più bassa, cioè lo stato ‘fondamentale’. Nella figura 1 la lunghezza λ di de Broglie è rappresentata dal raggio delle sferette incentrate sulla posizione media delle singole particelle. Nel caso classico essa risulta inferiore alla distanza media d tra gli atomi, mentre nel caso quantistico la temperatura (inferiore alla temperatura critica) è tale che λ risulta dell’ordine di d, circostanza che prevede zone di sovrapposizione tra le funzioni d’onda dei singoli atomi (zone tratteggiate). Questa sovrapposizione induce un comportamento globalmente quantistico del sistema; gli atomi che occupano lo stato fondamentale sono de;scritti dalla medesima funzione d’onda, e quindi gli effetti quantistici ondulatori tipici del singolo atomo sono presenti simultaneamente per un numero enorme di atomi, cosicché l’effetto complessivo risulta osservabile su scala macroscopica. Per es., la densità di probabilità caratteristica del singolo atomo che fornisce un’indicazione statistica della posizione dell’atomo stesso diviene una vera e propria densità macroscopica della materia. Di conseguenza, come i singoli atomi manifestano proprietà ondulatorie associate alla loro funzione d’onda e alla lunghezza di de Broglie, così la densità di materia di un condensato di Bose-Einstein può presentare massimi e minimi osservabili macroscopicamente, dovuti a un’interferenza ondulatoria di natura esclusivamente quantistica.

Dal mondo microscopico al mondo macroscopico: il gatto di Schrödinger

Allo scopo di interpretare la realtà fisica per mezzo della meccanica quantistica, è necessario analizzare il modo in cui i fenomeni possono essere suddivisi in microscopici e macroscopici, intendendo per macroscopico, come accennato in precedenza, tutto ciò che è direttamente osservabile mediante un apparato di misura. In altri termini, dato che la meccanica quantistica descrive la natura nella sua totalità, lo stesso apparato di misura macroscopico dev’essere descritto quantisticamente. Nell’effettuare tale analisi, una particolare attenzione va posta al necessario passaggio dal microscopico (un numero limitato di particelle) al macroscopico (apparato di misura e osservatori composti da un enorme numero di particelle). Infatti, se si trascura questo passaggio e si applica in maniera superficiale la meccanica quantistica, si possono ottenere interpretazioni e predizioni non corrette dei fenomeni. Il più illustre esempio di ciò è il cosiddetto gatto di Schrödinger. Si tratta dell’esempio di uno schema sperimentale che sembra implicare la possibilità di generare la sovrapposizione di due stati quantici profondamente differenti a livello macroscopico, con le conseguenze paradossali che ne seguono. Infatti, il gatto in questione (l’oggetto macroscopico) è chiuso in una scatola contenente una fiala di cianuro sigillata e un nucleo radioattivo (l’oggetto microscopico) il cui decadimento attiva un martello che, urtando la fiala, ne provoca la rottura con conseguente uscita del cianuro e morte del gatto. Lo stato macroscopico del gatto sembrerebbe quindi la sovrapposizione lineare degli stati gatto vivo (nucleo non decaduto) e gatto morto (nucleo decaduto), un’ambiguità che si risolverebbe a favore di uno dei due stati solamente all’apertura della scatola.

Questa interpretazione non è corretta. In effetti, affinché il decadimento di un singolo nucleo inneschi l’azione del martello è necessario un processo intermedio di amplificazione, e quindi l’argomento della generazione dello stato del gatto richiede un’analisi approfondita di tale processo. Quest’analisi tiene conto dell’inevitabile interazione dell’atomo con l’ambiente circostante insita nel processo di amplificazione (teoria della decoerenza), e permette di tenere traccia di ciò che accade, dal livello microscopico a quello macroscopico, e di verificare come non soltanto lo stato finale sia costituito o dallo stato gatto morto o da quello gatto vivo (e non dalla sovrapposizione di entrambi), ma come, anche a ogni istante precedente l’eventuale azione letale del segnale atomico amplificato, il gatto stesso sia vivo.

Ci si può chiedere in che modo la natura e i nessi di causa-effetto possano subire una tale profonda modifica nel passaggio dall’atomo al cianuro, ovvero dal microscopico al macroscopico. In realtà, ciò è correlato al processo di amplificazione dell’iniziale fenomeno a livello atomico, necessario al fine di ottenere l’effetto macroscopico, e questa amplificazione richiede energia che può solamente essere ottenuta mediante interazione con l’ambiente. Questo ambiente introduce un rumore casuale connesso all’amplificazione, del quale non si è tenuto conto nell’analisi non corretta che porterebbe all’irrealistica sovrapposizione quantistica degli stati gatto vivo e gatto morto. Il gatto di Schrödinger ci offre un esempio del modo in cui nella grande maggioranza dei casi si passa dal fenomeno microscopico alla sua misura necessariamente macroscopica, senza uscire dai binari dell’interpretazione quantistica.

Più in generale, la teoria della decoerenza descrive le interazioni spontanee dell’ambiente con il sistema in esame che portano alla soppressione dei fenomeni di interferenza tra differenti componenti della funzione d’onda, i quali costituiscono l’espressione fondamentale della meccanica quantistica. Nel caso particolare delle operazioni di misura, questa teoria può spiegare come l’apparato macroscopico, anche se necessariamente descritto in termini quantistici, sia in grado di fornire un risultato univoco. Ciò costituisce una soluzione al problema stesso del collasso della funzione d’onda all’atto della misura, e dell’emergenza del mondo classico dalla meccanica quantistica.

Non località in meccanica quantistica: il paradosso EPR

figura 2

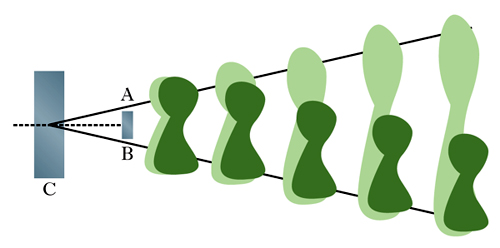
Un ulteriore elemento di differenza concettuale tra la fisica classica e la meccanica quantistica è connesso al cosiddetto principio di località (di Einstein), secondo il quale non è ragionevole pensare che un dato fenomeno fisico possa avvenire indipendentemente dalla distanza dall’evento che lo ha causato. Nelle pieghe degli assiomi della meccanica quantistica si può prevedere invece un caso nel quale il suddetto principio è, almeno in un certo senso, violato. A ciò si attribuisce comunemente il nome di non località quantistica. Al fine di porre in evidenza tale non località, Albert Einstein, Boris Podolsky e Nathan Rosen, basandosi sugli assiomi della meccanica quantistica, formularono un esperimento concettuale (il citato paradosso EPR) secondo il quale, a meno di violare il principio di indeterminazione, una misurazione su una particella ha un effetto su una seconda particella arbitrariamente distante dalla prima. Lo schema è illustrato nella figura 2: nel sistema C, da una singola particella viene prodotta una coppia di particelle (fotoni o elettroni), una delle quali percorre la traiettoria A mentre l’altra percorre la traiettoria B. Affinché le due particelle soddisfino il principio di indeterminazione, si può dimostrare che tra di esse deve esistere una correlazione a prescindere dalla loro distanza (zona tratteggiata in verde chiaro). Viceversa, se fosse valido il principio di località in senso stretto, qualunque tipo di influenza (zona tratteggiata in verde scuro) della particella B sulla particella A non potrebbe avere un raggio di azione arbitrario. In altre parole, se assumiamo che il principio di località abbia validità assoluta, questo esperimento rappresenta una violazione del principio di indeterminazione, e quindi una critica alle basi della meccanica quantistica stessa. Benché tale critica sia stata confutata dai principali esponenti della scuola di Copenaghen, il paradosso EPR ha costituito un argomento particolarmente costruttivo per alcuni successivi sviluppi della meccanica quantistica, e la sua descrizione è particolarmente indicata per chiarire la sostanziale differenza tra la visione classica e quella quantistica del mondo.

Come primo passo, si consideri l’esempio elementare di un tale che compri un paio di guanti e decida di inviare uno dei due, il destro o il sinistro, per posta a un amico residente in una città lontana, tenendo l’altro presso di sé in una busta chiusa. Nel momento in cui l’amico, preventivamente informato della spedizione, apre la busta, egli sa immediatamente quale guanto è rimasto presso il mittente e può comunicarglielo senza che ciò provochi il minimo stupore: è infatti evidente che il guanto che ha ricevuto, destro o sinistro che sia, è sempre stato nella busta, e non è necessario ipotizzare alcuna forma di influenza a distanza tra i guanti. Se invece che con due guanti (macroscopici), quanto sopra avviene con una coppia di particelle microscopiche che hanno, come i due guanti, per qualche motivo un nesso prestabilito (per es., se in seguito a una misura una presenta una proprietà destrogira, l’altra dovrà necessariamente presentarla levogira), ma si trovano in due buste distinte, ovvero in zone spaziotemporali diverse (particelle in uno stato entangled, ingarbugliato), la visione quantistica impone che il contenuto delle buste sia privo di significato (non faccia parte della realtà fisica) finché almeno una di esse non viene aperta. Solo all’atto della sua apertura (cioè della misurazione) la particella rimasta al mittente acquisisce la caratteristica di essere quella con proprietà destrogira o levogira, qualunque sia la distanza tra le due buste.

In effetti, secondo l’interpretazione di Copenaghen, le particelle nelle due buste (lo stato) sono in una sovrapposizione con uguale peso delle due potenzialità possedute (particella con proprietà destrogira nella busta spedita e particella con proprietà levogira in quella rimasta, o particella con proprietà levogira nella busta spedita e particella con proprietà destrogira in quella rimasta), e solo al momento dell’apertura di una busta, per es. quella ricevuta, lo stato complessivo delle due particelle acquista una proprietà sensibile, vale a dire collassa in una delle due potenzialità, come se l’osservazione di una particella potesse influenzare lo stato dell’altra indipendentemente dalla loro distanza.

Per chiarire come questa violazione della località sia necessaria per la consistenza della meccanica quantistica, ovvero perché abbia validità il principio di indeterminazione, si consideri il caso più complesso nel quale un tale compri invece che un solo paio di guanti, due paia di colori diversi (rosso e azzurro). Tra questi quattro guanti egli ne seleziona uno sinistro e uno destro di diverso colore, e con questi due esegue la stessa operazione di invio descritta precedentemente, ovvero ne manda uno all’amico. Di nuovo, l’amico, dopo avere osservato il guanto che gli è arrivato, conosce immediatamente lo stato del guanto rimasto presso il mittente. In questo caso, lo stato di ogni guanto è l’insieme di due proprietà, ovvero il verso e il colore. Nel caso analogo di due particelle microscopiche, s’intende che esse siano singolarmente descritte da due grandezze fisiche distinte (invece di una sola), e che esista un prestabilito nesso tra ciascuna di queste grandezze (come nel caso dei guanti, se una delle due risulta sinistra, l’altra risulta sempre destra, e se una risulta azzurra l’altra risulta sempre rossa). Se ora le due grandezze fisiche sono, per es., la posizione lungo un’asse e il corrispondente impulso delle singole particelle, ovvero sono grandezze legate dal principio di indeterminazione, accade che, a causa del nesso iniziale tra le due particelle, la scelta di misurare la posizione della particella nella zona A (busta inviata) consente di conoscere con sicurezza la posizione della particella nella zona B (busta rimasta), generando, per conseguenza del principio di indeterminazione stesso, una corrispondente incertezza sul suo impulso. Ugualmente, scegliendo di effettuare una misura dell’impulso della particella nella zona A, si conosce con sicurezza l’impulso della particella nella zona B, e si genera una corrispondente incertezza sulla sua posizione. D’altra parte, ipotizzando che sia valido il principio di località, la scelta di misurare in A la posizione o l’impulso non può avere conseguenze sulla particella in B, e questo significa che posizione e impulso della particella in B devono avere, per es., un valore preciso contemporaneamente, in violazione del principio di indeterminazione. In altre parole, o sussiste un’inconsistenza interna della meccanica quantistica (violazione del principio di indeterminazione), o il principio di località è violato.

Di conseguenza, se supponiamo valida la meccanica quantistica, e quindi il principio di indeterminazione, dobbiamo accettare il fatto che, siccome le due particelle sono correlate (stato entangled), all’atto in cui una particella viene osservata anche lo stato dell’altra collassa nella potenzialità complementare. Ciò sembrerebbe discutibile, in quanto le due particelle si trovano a distanza arbitraria l’una dall’altra, ed è lecito chiedersi con quale meccanismo l’azione della misurazione su una delle due possa influenzare lo stato dell’altra.

In realtà, l’analisi del processo mette in evidenza che non vi è nesso di causa-effetto tra le due particelle, nel senso che, pur sussistendo una correlazione a distanza tra di esse, la natura di questa correlazione è tale da escludere che un’osservazione in B dia informazione non ambigua su ciò che è avvenuto alla particella in A (ovvero se la particella in A sia stata precedentemente osservata o meno). In altre parole, non vi è modo di utilizzare una misura in A per inviare un segnale (non ambiguo) in B. Questa assenza di nesso causale in realtà sussiste qualunque sia la distanza tra A e B. In questi termini, è ora possibile riconciliare un principio di località con la meccanica quantistica, ove tale principio non si riferisca genericamente a correlazioni, ma sia limitato a veri e propri nessi di causa-effetto, ovvero neghi l’esistenza di meccanismi capaci di inviare segnali da A a B, indipendentemente dalla distanza, per mezzo di sole operazioni di misura in A. Osserviamo, tra l’altro, che l’eventuale violazione del principio di località per gli effetti capaci di trasportare segnale avrebbe, come conseguenza, la possibilità di trasmettere informazione in modo istantaneo, contravvenendo al limite imposto dalla relatività (la massima velocità in natura è quella della luce).

Sebbene sia possibile confutare il paradosso EPR, esso costituisce una critica particolarmente costruttiva per alcuni successivi sviluppi della meccanica quantistica, in particolare in quanto pone in evidenza l’importanza degli stati entangled. In effetti, la definizione di stato entangled (in tedesco verschrankte Zustande) è stata introdotta da Schrödinger come commento al paradosso EPR: «Quando due sistemi, dei quali conosciamo i rispettivi stati, interagiscono temporaneamente mediante forze note, e quando dopo un periodo di influenza mutua si separano nuovamente, essi non possono più essere descritti come prima, cioè, attribuendo a ciascuno di essi un suo stato caratteristico» (Discussion of probability relations between separated systems, «Mathematical proceedings of the Cambridge philosophical society», 1935, 31, 4, p. 555). Egli inoltre identifica ciò come l’aspetto fondamentale della meccanica quantistica: «Io non definirei questo un, ma piuttosto il tratto caratteristico della meccanica quantistica, ovvero quello sul quale si basa la sua totale dipartita dalle linee del pensiero classico. Per mezzo dell’interazione, le due rappresentazioni (gli stati quantici) sono diventati entangled» (p. 555).

Effetti non locali, disuguaglianze di Bell e stati entangled

La meccanica quantistica rappresenta una visione del mondo radicalmente diversa da quella tradizionale fornita dalla fisica classica. Tuttavia, il concetto di probabilità alla base delle predizioni quantistiche è presente anche in fisica classica, nell’ambito dell’interpretazione di alcuni fenomeni, e costituisce la base della cosiddetta meccanica statistica. Per es., il lancio di un dado da gioco coinvolge una tale quantità di dati non controllabili che è possibile fornire soltanto una descrizione probabilistica del risultato, ripetendo un gran numero di volte il lancio. In realtà, secondo le leggi della meccanica classica, è concettualmente lecito pensare di poter controllare l’enorme quantità di effetti connessi con il singolo lancio, e quindi predire con crescente certezza il risultato, per es. calcolando la traiettoria esatta del dado. In questo senso, la meccanica statistica rappresenta per la fisica classica solamente un ausilio che consente una predizione semplice e significativa, benché parziale, del fenomeno. Come già notato, la meccanica quantistica introduce un concetto di stato microscopico nell’ambito del quale la misura di una grandezza fisica può anche non essere prevedibile a priori, ma ci si deve limitare a stimare la probabilità di ottenere un dato valore. È naturale chiedersi se ciò sia un limite intrinseco della natura o se sia dovuto alla presenza di variabili nascoste, ovvero di parametri a noi non accessibili. Se ciò fosse vero, la natura mostrerebbe un’incertezza e risulterebbe descrivibile solo in modo statistico per il semplice fatto di non poter accedere a tutta l’informazione teoricamente esistente, come nel caso classico del lancio del dado. In sostanza, si potrebbe sostituire al principio di indeterminazione una corrispondente incertezza dovuta alla nostra ignoranza sulle variabili nascoste. Mentre per fenomeni locali questa interpretazione sembra del tutto equivalente alla meccanica quantistica tradizionale, nel caso di esperimenti del tipo EPR essa permetterebbe di rinunciare al principio di indeterminazione e quindi di conciliare il principio di località con la natura non deterministica del mondo microscopico (teoria quantistica locale). In realtà, proprio l’analisi di esperimenti del tipo EPR dimostra che, a differenza dei casi locali, le previsioni delle due teorie (meccanica quantistica tradizionale e analisi a variabili nascoste) differiscono tra loro. In particolare, l’introduzione di variabili nascoste implica che una serie di disuguaglianze (disuguaglianze di Bell) debbano essere soddisfatte, mentre tale condizione non è presente nella meccanica quantistica tradizionale. Gli esperimenti finora eseguiti (per es., quelli di Alain Aspect, Philippe Grangier e Gérard Roger) sembrano dare ragione alla meccanica quantistica, violando sistematicamente le disuguaglianze di Bell. La conseguente esclusione dell’esistenza di variabili nascoste comporta la validità del principio di indeterminazione, fatto che, come conseguenza dell’esperimento EPR, implica l’esistenza di correlazioni a distanza. Anche se, questa correlazione tra due particelle distanti, corrispondente all’esistenza di stati entangled, non consente l’invio di un segnale, è naturale chiedersi se essa possa dar luogo a fenomeni di interesse concettuale e applicativo. Questi, a causa della non esistenza delle variabili nascoste, saranno di natura esclusivamente quantistica, ovvero non interpretabili classicamente. Di recente, è stata ipotizzata e dimostrata sperimentalmente una serie di effetti associati all’entanglement (v. oltre Nuove applicazioni tecnologiche: Elettromeccanica quantistica).

Nuove applicazioni tecnologiche

Come già osservato, le basi concettuali della meccanica quantistica sono intrinsecamente differenti da quelle della fisica classica, e non ne rappresentano un semplice perfezionamento. Per es., la natura statistica delle predizioni non può in alcun modo essere ricondotta a un’interpretazione basata sul concetto classico di probabilità, come dimostrato nel 1965 da John S. Bell e in seguito comprovato da vari esperimenti. Un secondo aspetto consiste nella non località quantistica. Di conseguenza, è naturale chiedersi se queste differenze, concettuali oltre che puramente quantitative, possano consentire la progettazione di schemi applicativi, vere e proprie macchine quantistiche, non concepibili né simulabili classicamente. Di seguito saranno discussi alcuni di tali schemi.

Generatori di numeri casuali

Consideriamo il lancio di una moneta (testa o croce). Quando sosteniamo che la probabilità che esca testa (o croce) è del 50%, assumiamo che non sia possibile accedere all’insieme di informazioni che consentirebbero, tramite le leggi della meccanica, di sapere con certezza se uscirà testa o croce (ovvero la traiettoria della moneta). Nessun principio della fisica classica vieta che questa informazione sia a disposizione. Per es., un lanciatore abile e disonesto potrebbe scegliere di lanciare la moneta sempre in modo tale che la probabilità che esca testa sia superiore alla probabilità che esca croce, o viceversa. In termini generali, non esiste alcuno schema di macchina classica capace di generare rigorosamente numeri a caso. Analogamente, i numeri casuali generati da un computer per sistemi crittografici di protezione dati non sono in realtà completamente casuali, e possono essere in teoria previsti conoscendo le caratteristiche del calcolatore stesso. In altre parole, come ogni lancio di una moneta è inevitabilmente diverso dagli altri, così non esistono due computer uguali.

Una tale identità è possibile nel mondo descritto dalla meccanica quantistica. Consideriamo il caso di un insieme di elettroni con spin orientato in una determinata direzione. Misurando lo spin di ciascuno di essi in una direzione ortogonale, abbiamo la probabilità del 50% di trovarlo in un verso o in quello opposto, e la meccanica quantistica impone che non vi sia alcuna possibilità di predire il risultato di ogni singola misura. In questo senso, i risultati di queste misure (+1, −1) sono eventi assolutamente casuali, a differenza di quanto avviene lanciando monete o utilizzando altre macchine classiche per generare numeri casuali. Per es., elettroni aventi in comune il valore iniziale dello spin sono identici tra loro, ma tale identità è inaccessibile ai sistemi macroscopici della meccanica classica. Di conseguenza, è possibile progettare una macchina che generi numeri rigorosamente casuali utilizzando un’opportuna misura dello spin di una particella, e questo costituisce l’esempio più semplice di macchina o tecnologia quantistica.

Informazione quantistica

Uno degli elementi fondamentali della tecnologia moderna è connesso con la possibilità di utilizzare quantità che descrivono compiutamente un oggetto macroscopico. Queste quantità costituiscono ciò che viene denominato il suo contenuto informativo. Tutte le operazioni utili basate sull’utilizzo di questa informazione, copiandola, amplificandola, manipolandola, rappresentano la cosiddetta tecnologia dell’informazione. Visto che l’informazione deriva direttamente da atti di misurazione, ci si aspetta che essa e la sua manipolazione siano profondamente diverse in ambito quantistico, ovvero per sistemi microscopici. In particolare, la meccanica quantistica impone che la misurazione di uno stato microscopico sconosciuto non solo induca una modifica irreversibile dello stato del sistema, ossia del sistema stesso, proiettandolo in una delle molteplici possibilità previste dalla sua originaria funzione d’onda, ma fornisca anche una descrizione del tutto incompiuta dell’oggetto microscopico nel suo stato iniziale. Si è quindi recentemente ipotizzata la possibilità di realizzare macchine informatiche quantistiche che, invece di far uso di un’informazione codificata in stati macroscopici ottenuti tramite misure, ricorra a informazione contenuta in sistemi microscopici opportuni, che hanno interagito con l’oggetto in questione. Mentre gli elementi basilari dell’informazione classica sono i cosiddetti bit (variabili che possono assumere solo i due valori 0 e 1), gli elementi dell’informazione quantistica sono stati di sistemi microscopici, detti qubit, ovvero funzioni d’onda che rappresentano gli infiniti stati di sovrapposizione quantistica di due autostati di base, corrispondenti ai due possibili valori assunti da una grandezza, per es. la proiezione dello spin di un elettrone lungo una determinata direzione. La tecnologia dell’informazione quantistica è associata a operazioni e manipolazioni microscopiche effettuate su questi qubit. Mentre in generale la tecnologia classica ha ormai raggiunto livelli di sofisticazione elevati, quella quantistica è agli albori, e i progressi più avanzati coinvolgono al massimo operazioni su qualche decina di qubit. Tuttavia, macchine calcolatrici quantistiche sono in grado di effettuare operazioni concettualmente impossibili per macchine classiche, dando luogo a quello che viene chiamato un computer quantistico (v. oltre Computazione quantistica).

Prescindendo dalla difficoltà pratica di manipolare i qubit, l’informazione quantistica deve obbedire a leggi e limiti molto diversi rispetto al caso classico. In effetti, per quanto riguarda per es. l’operazione informatica fondamentale, ovvero la riproduzione dell’informazione, in base ai principi della meccanica quantistica si dimostra che non esiste alcun processo in grado di replicare lo stato ignoto di un sistema, mediante l’ausilio di un opportuno sistema analogo al primo, senza alterare in modo incontrollabile lo stato del sistema originario (quantum no cloning theorem). In definitiva, le operazioni informatiche che fanno uso di copie nel regime microscopico riguardano uno scenario che è stato inevitabilmente alterato. È evidente che in regime macroscopico questo problema è inessenziale, in quanto l’alterazione che subisce un sistema in seguito alla sua osservazione può essere resa praticamente trascurabile. Tornando al regime microscopico, se fosse possibile generare un numero sufficiente di copie di uno stato quantico arbitrario, esse potrebbero essere usate, al limite tutte tranne una, per arrivare a conoscere con sufficiente completezza lo stato, originariamente ignoto, avendo ancora un esemplare del sistema nello stato quantico iniziale. Il teorema del no cloning nega questa possibilità, in quanto l’effettuazione di ogni copia altera lo stato originario. Tale limite, che in generale non consente di riprodurre tutte le operazioni accessibili all’informatica classica, tuttavia permette, per es., la completa protezione di dati durante la loro trasmissione tramite la tecnica della crittografia quantistica (v. oltre). Notiamo inoltre come il fatto di copiare l’informazione sia alla base della sua trasmissione a distanza, e come il no cloning ponga in dubbio la possibilità di realizzare reti di informazione quantistica distribuite (telecomunicazioni quantistiche). In effetti, come vedremo, l’introduzione dello schema del teletrasporto quantistico mostra come sia possibile trasferire a distanza un qubit senza violare le leggi della meccanica quantistica, ovvero senza in realtà clonare lo stato originario.

Crittografia quantistica

Un sistema crittografico viene usato per proteggere l’informazione durante una comunicazione; in altre parole, per inviare un’informazione a un ricevente senza che questa venga intercettata da terzi. Un secondo aspetto della sicurezza del collegamento è associato alla possibilità di sapere se l’eventuale indesiderata intercettazione ha avuto luogo. Mentre nei sistemi classici è sempre possibile per un intercettatore abbastanza abile captare l’informazione senza che gli utenti ne vengano a conoscenza, ciò è reso invece impossibile dall’uso di opportuni sistemi quantistici di comunicazione.

Supponiamo che A voglia trasmettere un messaggio a B. Tutti sanno che il messaggio verrà trascritto nel valore della proiezione dello spin degli elettroni trasferiti da A a B, lungo l’asse x o l’asse y, secondo una scelta casuale di A per ciascun elettrone della sequenza. Nel leggere lo stato degli elettroni, B misura ogni spin nella direzione x o nella direzione y, anch’esso in maniera casuale. Avvenuta la trasmissione della sequenza, A dichiara pubblicamente quale asse ha usato per ogni singolo elettrone. A questo punto, per gli elettroni per i quali B ha usato lo stesso asse di A, B stesso ha ricevuto un’informazione. Per gli altri elettroni, B non ha ricevuto alcuna informazione, in quanto, a causa del principio di indeterminazione, dalla misurazione dello spin lungo un dato asse nulla si può inferire sul risultato di una misurazione successiva lungo un asse ortogonale. Per questi dati non trasferiti, B può richiedere la ritrasmissione ad A. Immaginiamo ora che un intercettatore C voglia conoscere l’informazione trasmessa da A. A tale scopo, egli non può che usare l’elettrone in questione, effettuando su di esso una misurazione analoga a quella che dovrebbe effettuare B. Tuttavia, poiché una tale misurazione ha una probabilità del 50% di cambiare lo stato dell’elettrone, egli non può sapere se un tale cambiamento abbia effettivamente avuto luogo. Di conseguenza, se egli invia l’elettrone osservato a B, sperando che B stesso non si accorga dell’avvenuto tentativo di intercettazione, la possibile modifica dello stato non gli dà la sicurezza che B non si accorga dell’intercettazione avvenuta. Infatti, a questo punto la presenza dell’eventuale intercettatore può essere rilevata nel seguente modo: per alcuni dei dati trasmessi, A dichiara pubblicamente il valore dei dati stessi, in modo tale che B possa averne la certezza. Confrontando i dati che ha ricevuto e per i quali aveva precedentemente selezionato in maniera casuale lo stesso asse di A, B si rende conto se ci sia stata intercettazione osservando discrepanze nei dati ricevuti nei casi in cui invece C aveva, casualmente, selezionato un asse diverso sia da A sia da B, modificando lo stato stesso. In effetti, l’intercettatore, al fine di non essere scoperto, dovrebbe ritrasmettere a B un elettrone nello stesso stato in cui lo ha sottratto. Ciò sarebbe possibile se C potesse fare una copia esatta dello stato dell’elettrone in questione, procedere quindi a effettuare la misurazione su uno dei due e ritrasmettere a B l’altro. Tale operazione, ovvero la duplicazione di uno stato quantico ignoto, non è possibile in virtù del teorema del no cloning.

Teletrasporto

Un problema che ha sempre affascinato la scienza è la possibilità di ottenere una replica esatta di un oggetto a distanza senza ricorrere al suo banale trasporto. Ciò che si intende trasmettere è l’informazione che caratterizza l’oggetto stesso, ovvero il suo stato fisico, al fine di poterlo ricostruire a distanza con opportune operazioni. In realtà, non conoscendo a priori lo stato, la meccanica quantistica nega la possibilità di conoscerlo in alcun modo in futuro. Effettuando qualunque misurazione di una grandezza fisica, il risultato ottenuto ci fornisce solo un’informazione parziale su quello che era lo stato del sistema prima della misurazione. Di conseguenza, un teletrasporto basato sull’osservazione del sistema e sulla successiva trasmissione dei dati ottenuti al fine di ricostruirlo a distanza è impossibile. Per es., un fax ricostruisce a distanza lo stato originario solamente a grandi linee, che però sono quelle che bastano nel caso di un testo stampato. È comunque notevole il fatto che la meccanica quantistica stessa contenga la soluzione del problema. Immaginiamo che A voglia teletrasportare un elettrone (1) in uno stato di spin a lui ignoto a un operatore distante B. A e B hanno a disposizione due elettroni in uno stato entangled di spin noto, uno presso A, (2), e l’altro presso B, (3). A non effettua una semplice misurazione sull’elettrone (1), ma esegue un’opportuna misurazione combinata tra l’elettrone (1) e l’elettrone (2). Mentre questa misura non fornisce alcuna informazione sull’inconoscibile stato originario di (1), il suo risultato, trasmesso per via convenzionale (per es. tramite una telefonata) a B, consente a B stesso di ricostruire lo stato originario di (1) in A sull’elettrone (3) in B. In tal modo, il teletrasporto ha avuto luogo. Da notare che: lo stato dell’elettrone (3), ormai identico a quello originario di (1), rimane comunque ignoto; la misurazione effettuata da A ha inevitabilmente distrutto lo stato originario di (1), un fatto in accordo con il teorema del no cloning. In effetti, se tale distruzione non avesse avuto luogo, avremmo semplicemente clonato l’elettrone (1) mediante l’elettrone (3). Lo schema accennato si riferisce al sistema microscopico costituito da un elettrone, ma può essere in linea di principio esteso al teletrasporto di sistemi non necessariamente microscopici, anche se tale estensione è al momento puramente teorica.

Computazione quantistica

L’informazione rappresenta l’insieme dei risultati delle misurazioni effettuate su un sistema. Per un sistema macroscopico, questa informazione fornisce una rappresentazione esaustiva, a differenza di quanto avviene per quelli microscopici. Un ruolo analogo per i sistemi microscopici è svolto dalla funzione d’onda stessa che, benché inaccessibile, ne fornisce una rappresentazione completa. In questa analogia, la funzione d’onda viene detta informazione quantistica del sistema microscopico. Mentre l’informazione classica risulta non ambigua, ovvero, per es., un elemento di informazione classico (bit) può assumere solo il valore 1 o il valore 0, l’equivalente quantistico (qubit), ossia la funzione d’onda di uno spin, i cui possibili valori in seguito a una misurazione sono due, ovvero ‘su’ (lo stato 1) e ‘giù’ (lo stato 0), può invece essere in uno qualsiasi degli infiniti stati possibili di sovrapposizione dello stato 1 e dello stato 0. Per es., un qubit può essere partecipe contemporaneamente dello stato 1 e dello stato 0. Ciò comporta che, mentre un’operazione di computazione classica fornisce un unico risultato associato a precisi valori dei bit coinvolti, un’operazione di computazione quantistica equivale, per certi aspetti, a effettuare più operazioni simultaneamente. Un esempio importante, connesso con la ricerca del periodo di una funzione, consiste nel determinare se i valori di una funzione data per due diversi valori della variabile sono uguali o diversi. Un computer classico è costretto a calcolare la funzione nei due valori, compiendo così almeno due operazioni. Un computer quantistico invece può ottenere il risultato mediante un’unica operazione. Tale caratteristica è connessa al fatto che nei singoli passaggi dell’algoritmo di calcolo non sono effettuate misurazioni, oltre all’unica necessaria alla conclusione del calcolo stesso. Va notato che in molti altri algoritmi quantistici, l’atto finale di misura fornisce il risultato richiesto solo probabilisticamente, in accordo con la natura casuale della funzione d’onda. Ciononostante, per particolari algoritmi, quali la fattorizzazione dei numeri primi e la ricerca di un elemento in una lista, la computazione quantistica risulta di gran lunga più efficiente di quella classica.

Elettromeccanica quantistica

Uno dei problemi concettuali più importanti nell’ambito dell’interpretazione della meccanica quantistica è la transizione dal macroscopico al microscopico (o viceversa), ovvero dal mondo classico a quello quantistico. Tale interesse concettuale è accompagnato dalla necessità emergente di descrivere il comportamento quantistico di nanostrutture, quali risonatori nanomeccanici, transistor a singolo elettrone e qubit, le quali, utilizzando proprietà che non trovano un analogo diretto in fisica classica, potenzialmente possono divenire componenti fondamentali degli apparati elettronici della prossima generazione. In effetti, in condizioni particolari (quali temperature prossime allo zero assoluto), le scale spaziali dei singoli componenti diventano confrontabili con la loro lunghezza di de Broglie. Ciò implica la necessità di descrivere il comportamento delle nanostrutture in regime quantistico.

Molti degli aspetti singolari della meccanica quantistica, quale, per es., l’entanglement, non hanno un corrispondente macroscopico, e riguardano il regime microscopico proprio degli atomi e degli elettroni. Tuttavia, come notato precedentemente nel contesto del cosiddetto gatto di Schrödinger, anche i sistemi macroscopici possono esistere in una sovrapposizione di stati, difficile tuttavia da rivelare a causa della decoerenza indotta dall’ambiente. In effetti, evidenze di comportamenti quantistici in questi componenti sono state recentemente ottenute accoppiando a stati microscopici del campo elettromagnetico (fotoni) un sistema quantistico ‘macroscopico’, intendendo con tale termine oggetti di dimensioni inferiori al milionesimo di metro ma contenenti migliaia di miliardi di atomi: tali possono essere, per es., uno specchio mobile o un oscillatore meccanico costituito da una sottile barretta metallica incernierata a un’estremità (cantilever). La presenza o l’assenza d’interferenza nel sistema microscopico indica la presenza o l’assenza di un comportamento quantistico del sistema nano- e micrometrico. A tale scopo, la temperatura del sistema deve essere mantenuta molto bassa (pochi millikelvin), in modo da eludere le fluttuazioni termiche e rendere l’energia del cantilever prossima a quella dello stato fondamentale dell’associato sistema quantistico. Inoltre, i fenomeni di decoerenza associati all’interazione tra il sistema e l’ambiente che lo circonda, che portano inevitabilmente alla soppressione degli effetti d’interferenza tipici della meccanica quantistica, devono essere contenuti usando risonatori ad alto fattore di merito. In tali circostanze, il sistema inizia a manifestare un comportamento collettivo quantistico simile a quello associato ai singoli atomi e molecole.

Le auspicabili applicazioni dei risonatori nanomeccanici richiederanno un’analisi quantistica accurata di tali sistemi che dovranno tipicamente operare in condizioni prossime al limite quantico. Inoltre, la generazione e la rivelazione dei loro stati quantici, quali gli autostati dell’energia, gli stati sovrapposizione o gli stati entangled, dovrebbero contribuire a chiarire alcuni degli aspetti controintuitivi e paradossali della meccanica quantistica, usualmente riservati al mondo microscopico degli atomi, degli elettroni e dei fotoni.

Bibliografia

G.J. Milburn, Schrödinger’s machines. The quantum technology reshaping everyday life, New York 1997.

The physics of quantum information. Quantum cryptography, quantum teleportation, quantum computation, ed. D. Bouwmeester, A. Ekert, A. Zeilinger, Berlin 2000.

E. Joos, H.D. Zeh, C. Kiefer et al., Decoherence and the appearance of a classical world in quantum theory, Berlin 2003².

J.S. Bell, Speakable and unspeakable in quantum mechanics. Collected papers on quantum philosophy, Cambridge 2004² (trad. it. Milano 2010).