MECCANICA QUANTISTICA
MECCANICA QUANTISTICA.
- Interpretazione dei concetti. Formulazioni alternative e concorrenti. Problema della misura. Entanglement e non località. Limite classico. Computazione quantistica e crittografia quantistica. Bibliografia
Nonostante il successo, sancito dall’accurata verifica sperimentale, la m. q. è in contrasto con il senso comune e pone difficoltà interpretative, a livello fisico ed epistemologico, dando luogo a fraintendimenti e dispute attorno agli aspetti apparentemente paradossali della teoria. Si pensi al cosiddetto paradosso di Einstein-Podolski-Rosen (EPR), che si manifesta quando due particelle sono preparate in uno stato entangled (aggrovigliato), nel quale la misura di una proprietà di una delle due particelle influenza istantaneamente i possibili risultati delle misure eseguite sull’altra. Secondo la m. q., l’influenza permane anche quando le particelle sono molto lontane, senza però poter essere sfruttata per mandare un’informazione a velocità superiore a quella della luce. Quindi, tra l’entanglement quantistico e la relatività ristretta formulata da Albert Einstein vige una sorta di coesistenza pacifica.
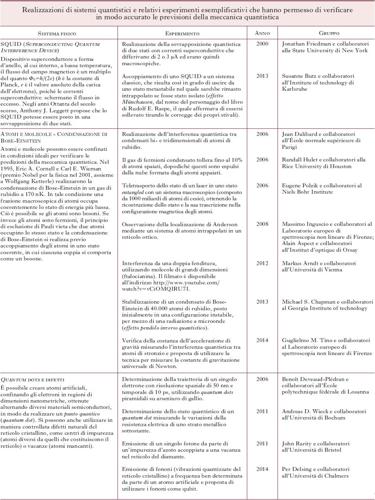
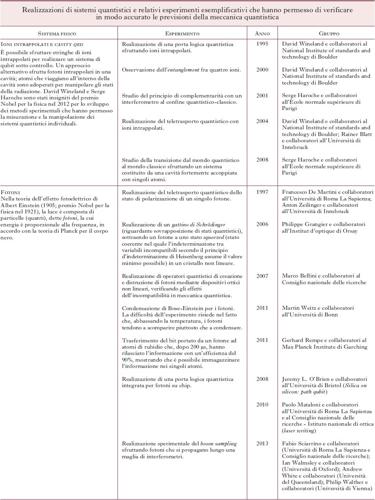
Negli ultimi dieci anni si sono compiuti notevoli progressi, sia teorici sia sperimentali, riguardanti l’interpretazione dei concetti della m. q., la connessione tra le varie formulazioni della teoria, il problema della misura, le proprietà degli stati entangled e la non località, e il problema dell’emergenza di proprietà classiche nei sistemi macroscopici (il cosiddetto limite classico). Lo sviluppo tecnologico ha consentito realizzazioni sempre più raffinate di sistemi quantistici, che rappresentano il banco di prova della teoria (v. tabella 1 e 2). Sul piano applicativo, senza elencare le numerose realizzazioni legate alle proprietà quantistiche dei materiali, gli sviluppi più recenti riguardano la computazione e la crittografia quantistica.
Interpretazione dei concetti. – Sin dal momento della formulazione della teoria, ci si è chiesti se le probabilità del la m. q. fossero di natura ontologica (cioè legate alla natura del mondo) oppure epistemologica (cioè legate, per es., alla nostra incapacità di completare in senso deterministico la m. q.). Alcuni autori hanno suggerito che la funzione d’onda sia un’entità fittizia (interpretazione epistemologica della funzione d’onda) e che il formalismo della m. q. rappresenti un mero artificio atto a calcolare le probabilità degli esiti dei processi di misura. Il tentativo di visualizzare la distribuzione di probabilità associata alla funzione d’onda si scontra con la difficoltà di evitare il collasso dello stato del sistema durante la misura.
Negli ultimi anni sono stati realizzati diversi esperi-menti con lo scopo di esplorare direttamente le proprietà della funzione d’onda. Nel 2013, Aneta S. Stodolna e i suoi collaboratori hanno visualizzato un orbitale dell’atomo d’idrogeno in campo elettrico, che può essere direttamente confrontato con la soluzione dell’equazione di Schrödinger. Nel 2014, un’équipe dell’Università di Rochester ha misurato coppie di variabili incompatibili per i fotoni di un laser, mostrando che il principio di indeterminazione, usualmente ricondotto al fatto che uno strumento accurato nel misurare la posizione, è poco accurato nel misurare la quantità di moto, e viceversa, ha un significato più profondo: informazioni dettagliate sulla posizione possono essere ottenute introducendo rumore nelle misure della quantità di moto. La distribuzione di quest’ultima è stata ottenuta direttamente, mentre la distribuzione della posizione è stata ricostruita, ottimizzando l’utilizzo dell’informazione ottenibile in un processo di misura, senza violare il principio di indeterminazione. L’altro aspetto, apparentemente paradossale, della m. q. è il dualismo onda-corpuscolo, cioè la manifestazione di proprietà ondulatorie o corpuscolari delle particelle, a seconda che se ne misuri la quantità di moto o la posizione. Nel 2015 un’équipe del Politecnico di Losanna ha studiato l’interazione tra radiazione elettromagnetica ed elettroni in un cavo metallico nanoscopico. Usando un microscopio elettronico si sono ottenute immagini che colgono il dualismo onda-corpuscolo della radiazione elettromagnetica in una singola misura.
Formulazioni alternative e concorrenti. – La m. q. ebbe inizialmente due formulazioni apparentemente alternative: quella di Erwin Schrödinger, basata sulla funzione d’onda, e quella di Werner Heisenberg, che rappresenta le proprietà misurabili di un sistema per mezzo di operatori, soddisfacenti una determinata legge di evoluzione temporale. In seguito, fu dimostrata l’equivalenza delle due formulazioni, e ne furono sviluppate altre, tra le quali quella di Richard Feynman, la quale mostra che una particella quantistica percorre, in qualche senso, tutte le traiettorie possibili tra due punti e solo in opportune condizioni emerge la singola traiettoria che l’esperienza comune attribuisce a un corpo. Questa formulazione, tra l’altro, contribuisce a chiarire il limite classico della meccanica quantistica. Sono state sviluppate anche teorie concorrenti della m. q., tra cui la meccanica di David Bohm, nella quale le particelle seguono traiettorie ben definite che sono soggette, oltre che alle forze convenzionali, anche a una forza quantistica, generata dalla funzione d’onda, che diventa così un campo agente sulle particelle. Tale forza oscilla fortemente su distanze molto piccole, rendendo necessaria una descrizione probabilistica del tutto equivalente a quella della meccanica quantistica.
Problema della misura. – Nella formulazione della m. q. i processi di evoluzione e di misura hanno caratteristiche contrapposte. Mentre l’evoluzione di un sistema chiuso (non interagente con l’ambiente) è descritta da un operatore unitario ed è dunque completamente deterministica, il processo di misura è intrinsecamente probabilistico. Un aspetto apparentemente paradossale del processo di misura in m. q. è il cosiddetto effetto di Zenone quantistico: l’evoluzione temporale di un sistema può essere congelata reiterando continuamente la misura di una grandezza, determinando di fatto un continuo collasso dello stato del sistema. L’effetto è stato studiato in diversi contesti. Nel 2004, James D. Franson e i suoi collaboratori hanno proposto di usarlo per risolvere alcuni problemi nell’approccio alla computazione quantistica basato sull’ottica lineare. Nel 2006 Erik W. Streed e i suoi collaboratori hanno studiato l’effetto in un condensato di Bose-Einstein di atomi di rubidio. Nel 2008 Javier Echanobe e i suoi collaboratori hanno mostrato che è possibile estrarre informazione sulla distribuzione dei tempi di arrivo di una particella in una data regione dello spazio mediante misure ripetute della posizione della particella. Un’altra questione riguarda la possibilità di visualizzare un sistema quantistico, senza distruggere il suo stato per effetto dell’osservazione. Nel 2010 André Kubetzka e i suoi collaboratori sono riusciti a visualizzare lo spin dell’elettrone di un atomo di cobalto mediante microscopio a effetto tunnel. Nel 2011 Michael R. Vanner e i suoi collaboratori hanno ottenuto istantanee dello stato quantistico di risonatori micromeccanici mediante impulsi rapidissimi di luce visibile.
Entanglement e non località. – Due aspetti cruciali della m. q. sono l’entanglement e la non località. L’entanglement consiste in una correlazione non locale tra sottoinsiemi del lo stesso sistema fisico, che non ha alcun analogo classico, e che contraddice i principi di realtà e località assunti da Einstein, Boris Podolski e Nathan Rosen nel 1935 e caratterizzanti la fisica classica. Essi proposero allora di ripristinare il principio di realtà ipotizzando che il risultato delle misure effettuate su sistemi quantistici entangled fosse già determinato, prima della misura stessa, dai valori assunti da variabili nascoste (cioè ignote all’osservatore) locali. Nel 1964 John Bell sviluppò un metodo formale per verificare la compatibilità fra le previsioni della m. q. e le teorie a variabili nascoste, attraverso opportune disuguaglianze matematiche. Tale sviluppo ha rappresentato la chiave di volta rispetto alle discussioni sulla completezza della teoria quantistica, e la dimostrazione sperimentale della violazione delle diseguaglianze di Bell ha confermato ulteriormente la validità della meccanica quantistica. I primi esperimenti su particelle entangled risalgono ai primi anni Ottanta del secolo scorso e sono stati effettuati nei laboratori di Orsay dai fisici Alain Aspect, Philippe Grangier e Gérard Roger. In tali esperimenti gli stati quantistici venivano generati attraverso i metodi dell’ottica non lineare, come fasci laser, cristalli e lamine di ritardo. La violazione delle disuguaglianze di Bell fu verificata con l’assunzione di alcune ipotesi di natura pragmatica (dette fair assumptions), che derivavano dalle inevitabili imperfezioni sperimentali, dimostrando così che i modelli a variabili nascoste non sono compatibili con le osservazioni sperimentali.
Sotto le ipotesi fatte, le predizioni della m. q. si sono invece rivelate corrette e hanno generato una nuova branca della ricerca fisica chiamata informazione quantistica.
Una questione fondamentale è se l’entanglement si possa manifestare in sistemi macroscopici. Tale argomento è stato oggetto di ricerca da parte di diversi gruppi. Fra i tanti, citiamo i risultati conseguiti nel 2008 presso i laboratori d’informazione quantistica di Roma, da Francesco De Martini e dai suoi collaboratori, che hanno studiato ciò che succede quando una coppia di due fotoni entangled viene amplificata. Nel 2010, Marco Bellini e i suoi collaboratori, all’Istituto nazionale di ottica di Firenze, hanno ottenuto l’entanglement di un impulso laser macroscopico con un fotone in un cristallo non lineare. Nel 2014, Tobias Denkmayr e i suoi collaboratori, utilizzando due fasci di neutroni, hanno messo in evidenza gli aspetti non intuitivi della non località: in opportune condizioni, i neutroni si comportano come se fossero spazialmente separati dalle loro proprietà osservabili. Nello stesso anno, Naeimeh Behbood e i suoi collaboratori hanno ottenuto l’entanglement per uno stato macroscopico in un campione di 500.000 atomi di rubidio, alla temperatura di 20 μK.
Un altro concetto cruciale in m. q. è quello di contestualità: il risultato della misura di una grandezza può variare se la misura viene eseguita contestualmente alla misura di un’altra grandezza con essa compatibile, a seconda della scelta di quest’ultima (cioè della configurazione sperimentale atta a misurarla contestualmente alla prima). La contestualità è stata studiata in maniera teorica da Adan Cabello, Simone Severini e Andreas Winter nel 2014. Nello stesso anno, Joseph Emerson e i suoi collaboratori hanno analizzato il ruolo della contestualità nella computazione quantistica.
Limite classico. – Se il mondo microscopico è descritto dalla m. q., come avviene il passaggio al mondo macroscopico, nel quale l’evidenza empirica mostra la validità del determinismo meccanico, ed esclude l’esistenza di grandezze mutuamente incompatibili? Diversi sono i fattori che possono condurre a tale transizione, tra cui l’accoppiamento del sistema in esame con l’ambiente circostante e le caratteristiche dell’apparato di misura. Nel 2007, Johannes Kofler e Časlav Brukner sono giunti alla conclusione che il passaggio dal mondo quantistico a quello classico non è un cambiamento di comportamento, ma è associato all’imprecisione della misura. In genere, tuttavia, l’imprecisione della misura può essere ricondotta al fatto che l’ambiente circostante esercita una forte influenza su un sistema quantistico e questa influenza è tanto meno controllabile (e misurabile) quanto più alta è la temperatura e quanto più grande è il numero di particelle che compongono il sistema. I fenomeni quantistici si manifestano su scala macroscopica soltanto se i cambiamenti che insorgono in una parte del sistema si trasmettono coerentemente senza violare le relazioni reciproche tra gli stati quantistici delle diverse parti. Il processo di distruzione della coerenza da parte dell’ambiente circostante è detto decoerenza. La teoria oggi forse più accreditata per la decoerenza è stata formulata da Wojciech H. Zurek a partire dagli anni Ottanta. In questa teoria, l’accoppiamento di un sistema quantistico con l’ambiente è descritto da un operatore (matrice densità) i cui elementi non diagonali descrivono i fenomeni di coerenza quantistica. Nel processo di decoerenza si produce il progressivo annullamento di tali elementi. Il tempo caratteristico in cui la decoerenza si manifesta dipende dal numero di gradi di libertà del sistema e dell’ambiente ed è tipicamente molto breve se l’ambiente è un sistema macroscopico non coerente. Una teoria alternativa è stata formulata nel 1986 da Gian Carlo Ghirardi, Alberto Rimini e Tullio Weber che proposero un’evoluzione modificata della funzione d’onda (un termine aggiuntivo nell’equazione di Schrödinger), tale da produrre collassi spontanei dello stato quantistico su scale di tempo lunghissime (dell’ordine di un miliardo di anni, quindi inosservabili) per una singola particella, che sarebbero però frequentissimi per sistemi composti da un numero macroscopico di particelle (per es., un collasso ogni nanosecondo per un sistema composto da 1024 particelle), in modo che la funzione d’onda di un sistema macroscopico sia a tutti gli effetti sempre collassata in uno stato classico.
Nel 2013, Alexander I. Lvovsky e collaboratori, partendo da due fotoni in uno stato entangled, hanno amplificato uno dei due fotoni fino a ottenere un sistema di 100 milioni di fotoni. Tornando allo stato iniziale, l’entanglement è rimasto, mostrando che è possibile mantenere la coerenza anche passando attraverso uno stato composto di un gran numero di costituenti.
Computazione quantistica e crittografia quantistica. – Il mondo moderno si basa sempre più sulla nostra capacità di gestire, trasmettere ed elaborare l’informazione. Mentre le tecnologie dell’informatica classica si stanno progressivamente avvicinando ai loro limiti fondamentali di potenza di calcolo, in diversi laboratori si sta lavorando alle tecnologie del futuro. Tra le più promettenti, c’è la tecnologia dell’informazione quantistica, che sfrutta le proprietà del mondo quantistico per eseguire operazioni che sarebbero impossibili secondo le leggi della fisica classica, come, per es., proteggere l’informazione codificata in modo assolutamente inviolabile (crittografia quantistica) oppure elaborarla in modo molto più rapido di quanto sarebbe possibile con un computer classico (computazione quantistica). La capacità del computer quantistico è quella di risolvere problemi che i computer classici non possono trattare (come la scomposizione in fattori di un numero molto grande), ma la sua realizzazione è ancora lontana.
Un altro settore di applicazione della fotonica è la comunicazione quantistica. Di norma, ogni fotone trasporta l’equivalente quantistico di un singolo bit di informazione, il cosiddetto qubit, che può valere ‘zero’ o ‘uno’ oppure trovarsi in un particolare stato quantistico che coinvolge una sovrapposizione di entrambi i valori (quest’ultima possibilità è esclusa per un bit classico). Diventa quindi necessario individuare opportuni passaggi intermedi che siano in grado di dimostrare il potenziale computazionale di un computer quantistico. Un esempio è il boson sampling (BS, «campionamento bosonico»), formulato nel 2010 da Scott Aaronson e Alex Arkhipov del Massachusetts Institute of technology di Boston: è possibile calcolare efficientemente la maniera in cui molte particelle bosoniche, come i fotoni (i quanti della luce), si propagano in strutture complesse? Mentre con un computer classico la risposta è negativa, con un simulatore quantistico questo problema dovrebbe essere risolvibile. Tale previsione teorica ha dato origine a una competizione internazionale per la realizzazione sperimentale di un primo dispositivo quantistico, basato sulla luce, in grado di risolvere il boson sampling. Nel 2013 quattro gruppi sperimentali hanno riportato indipendentemente la prima dimostrazione di un ‘semplice’ BS; fra questi una collaborazione tra ricercatori dell’Università di Roma La Sapienza e del Consiglio nazionale delle ricerche, che ha sviluppato nuovi dispositivi di fotonica integrata, ossia chip in grado di manipolare la propagazione della luce.
Bibliografia: Il mondo dei quanti, a cura di L. Lanz, «Le Scienze quaderni», 1993, 70; D.Z. Albert, Meccanica quantistica e senso comune, Milano 2000; Fenomeni quantistici, a cura di E. Beltrametti, «Le Scienze quaderni», 2000, 112; Filosofia della fisica, a cura di G. Boniolo, Milano 2000; A.D. Aczel, Entanglement: il più grande mistero della fisica, Milano 2004; E. Filoramo, A. Giovannini, C. Pasquero, Alla scoperta della crittografia quantistica, Torino 2006; G.C. Ghirardi, Un’occhiata alle carte di Dio. Gli interrogativi che la scienza moderna pone all’uomo, Milano 2009; J.S. Bell, Dicibile e indicibile in meccanica quantistica, Milano 2010; J. Bernstein, Salti quantici, Milano 2013; K.W. Ford, Il mondo dei quanti. La fisica quantistica per tutti, Torino 2014.