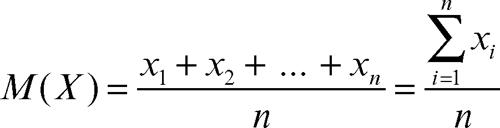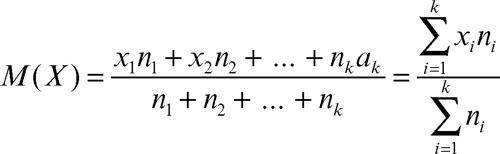media aritmetica

media aritmetica

media aritmetica indice di posizione in una distribuzione di dati statistici, tra i più utilizzati perché di facile calcolo: è quel valore che avrebbero i dati se essi fossero tutti uguali. È indicata con M(X), se si vuole specificare la variabile statistica X, oppure con µ: si utilizza invece la notazione x̄ quando si fa riferimento ad analisi campionarie. Se ogni modalità si presenta una sola volta nella distribuzione, si utilizza la media aritmetica semplice, definita come il rapporto tra la somma di tutti i valori assunti dalla variabile X e il numero totale n delle unità prese in considerazione

Se le modalità x_i si presentano ciascuna con frequenze assolute n_i, si utilizza la media aritmetica ponderata definita come il rapporto tra la somma dei prodotti di ciascun valore della variabile X per la rispettiva frequenza e la somma totale delle frequenze

dove k rappresenta il numero delle diverse modalità assunte dalla variabile X. La media aritmetica, che non necessariamente corrisponde a qualcuno dei dati, gode della proprietà di linearità, è cioè invariante per trasformazioni lineari dei dati: se X è una variabile statistica e p, q sono numeri reali, allora si ha M(pX + q) = p ⋅ M(X) + q. Per ogni valore x_i della variabile statistica X, è possibile definire uno scarto s_i dalla media, che indica il grado di scostamento del singolo valore da quello della tendenza centrale: s_i = x_i − M(X). La somma algebrica degli scarti dalla media è nulla.