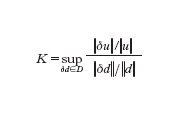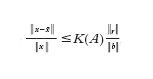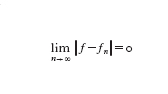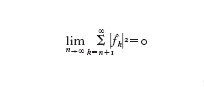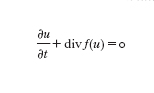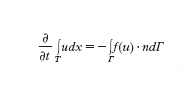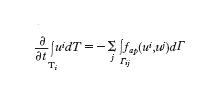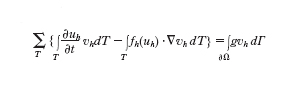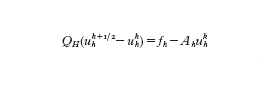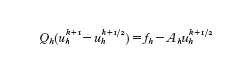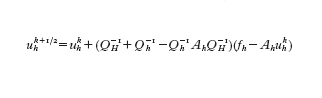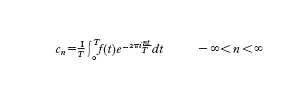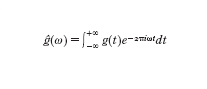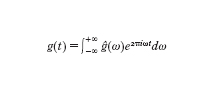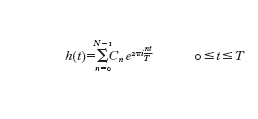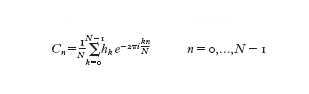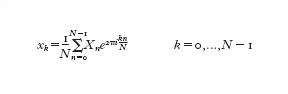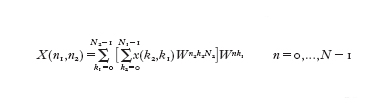Computazionali, metodi

Computazionali, metodi

I m. c. permettono di risolvere con calcolatori elettronici, all'interno delle scienze applicate, i problemi complessi che sono formulabili tramite il linguaggio della matematica. Tali problemi raramente sono risolubili per via analitica. In generale, la loro soluzione non ammette una rappresentazione in forma esplicita: basti pensare a equazioni o sistemi non lineari (algebrici, differenziali o integrali) di cui non siano note formule risolutive. In altri casi la forma esplicita, pur nota, non è praticamente utilizzabile per determinare valori quantitativi della soluzione stessa, o perché essa richiederebbe una quantità di operazioni proibitiva anche per i più moderni calcolatori elettronici, o perché espressa a sua volta attraverso altri enti matematici (quali integrali o sviluppi in serie) di cui sia difficile dare una valutazione quantitativa.

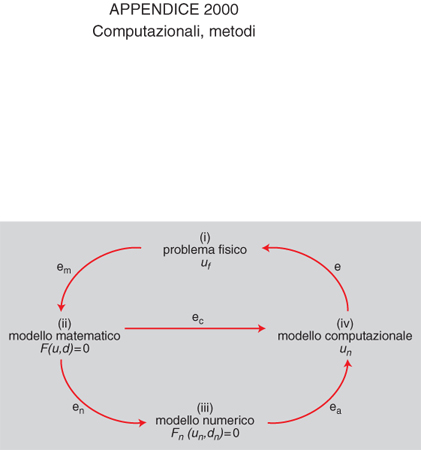
La risoluzione di problemi di interesse applicativo comporta diverse fasi: (i) l'interpretazione del problema; (ii) la sua modellazione attraverso equazioni matematiche che possono essere algebriche, funzionali, differenziali o integrali (modello matematico); (iii) l'individuazione di metodi della matematica numerica che siano idonei ad approssimare tale modello matematico (questa fase di approssimazione è indispensabile ogniqualvolta il modello matematico abbia una dimensione infinita e richieda pertanto di essere sostituito da una successione di problemi numerici ciascuno di dimensione finita (discretizzazione); (iv) l'implementazione di tali metodi numerici di approssimazione su calcolatori.

I m. c. comprendono ed esauriscono le fasi (iii) e (iv) del processo. La scelta di tali metodi non può prescindere da una conoscenza adeguata delle proprietà qualitative della soluzione del modello matematico e da una buona percezione della fenomenologia del problema originario. È pertanto giustificata la terminologia di modelli computazionali che viene usata in alternativa a quella di metodi computazionali. La modellistica computazionale è un settore di ricerca interdisciplinare, che si trova alla confluenza della matematica, dell'informatica e delle scienze applicate. La sua evoluzione è stata impetuosa negli anni recenti grazie al vigoroso sviluppo dei calcolatori e degli algoritmi, nonché a una maggior consapevolezza del ruolo che il calcolo scientifico può rivestire nella simulazione di complessi problemi di interesse scientifico/teorico, industriale, sociale.

fig.

Si può riassumere in forma schematica il processo (i)-(iv) con l'ausilio di un diagramma (v. fig.). Indichiamo con u_f la soluzione del problema originario, qui detto per brevità problema fisico, anche se si possono considerare problemi provenienti da tutte le scienze fondamentali e applicate (non solo dalla fisica), quali la chimica, le scienze biologiche e mediche, l'ingegneria, l'economia e così via.

Il modello matematico che descrive il problema fisico è posto nella forma F(u,d)=0, dove si suppone che d descriva l'insieme dei dati, u la soluzione, ed F la relazione funzionale che lega fra loro dati e soluzione (v. modellistica matematica, in questa Appendice). Vari e diversificati sono i problemi matematici che, in astratto, possono essere formulati in questo modo. Per citarne alcuni, si pensi all'integrazione definita di una funzione: si tratta di trovare un numero reale u tale che u=∫_R f, dove R è una regione del piano o dello spazio, ed f una funzione ivi integrabile (in questo caso i dati sono d={R, f} e la soluzione è data da u). Molto spesso la funzione f non è integrabile in modo elementare; inoltre il problema ha dimensione 'infinita', essendo l'integrale un processo esprimibile attraverso operazioni di passaggio al limite.

Un altro esempio è fornito dal problema: trovare u tale che P(u)=0, dove P(x)=Σ^r_k=₀ a_kx^k. Questa volta d={a₀,...,a_r} e u è l'insieme delle r radici complesse del polinomio P di grado r, la cui esistenza è assicurata dal teorema fondamentale dell'algebra. Pur essendo questo problema posto in dimensione finita, le sue soluzioni (le radici di P) non sono note in forma esplicita quando r è grande (per es. r≥5). Servono dunque metodi numerici che consentano di trovare valori approssimati di u.

Un altro problema è quello dell'integrazione di equazioni (o sistemi di equazioni) differenziali ordinarie della forma u^(q)(x)=G(x,u,u⁽¹⁾,...,u^(q⁻¹⁾), per x∈I⊂R, con u(x₀)=u₀, u⁽¹⁾(x₀)=u₁,...,u^(q⁻¹⁾(x₀)=u_q₋₁, dove I è un intervallo della retta reale, u è una funzione (scalare o vettoriale) della variabile x, u^(k)(x) denota la sua derivata k-esima, q≥1 rappresenta l'ordine del problema differenziale, G è una funzione (lineare o non rispetto alle sue variabili) e, infine, u₀, u₁,...,u_q₋₁ sono i cosiddetti dati iniziali assegnati nel punto x₀. L'insieme complessivo dei dati è espresso da d={I,G,x₀,q,u₀,...,u_q₋₁} e la soluzione è la funzione u; vi sono dei teoremi che assicurano l'esistenza e l'unicità della soluzione sotto certe condizioni, ma anche qui può essere necessario od opportuno applicare i metodi numerici o computazionali. Anche in questo caso il modello matematico è formulato in dimensione infinita (per via della presenza delle derivate) e necessita di essere ricondotto al finito attraverso processi di discretizzazione delle derivate stesse: in seguito a ciò la funzione incognita u, quasi mai nota in forma esplicita, sarà sostituita da un vettore che ne approssima i valori in punti prestabiliti (detti nodi) nell'intervallo I.

Infine, possiamo citare l'insieme dei problemi differenziali, stazionari o evolutivi, esprimibili attraverso derivate parziali; questi problemi sono di notevole importanza nella risoluzione di problemi applicativi. Anche in questo caso si tratta di problemi di dimensione infinita, la cui discretizzazione può essere basata su criteri di approssimazione i quali si ispirano direttamente alle caratteristiche del problema fisico originario. Svariati altri modelli matematici sono oggetto di interesse per la modellistica computazionale. Si pensi, per es., al problema della rappresentazione di curve e superfici, al trattamento numerico di immagini e segnali, alla minimizzazione di funzionali liberi o vincolati, alla regolarizzazione numerica e risoluzione di problemi inversi, ai problemi integro-differenziali, nonché al controllo di sistemi differenziali, integrali o di natura stocastica. La rilevanza di tali modelli nell'analisi e simulazione di processi meccanici (per es., nella fluidodinamica, nell'analisi strutturale, nella bioingegneria), fisici (nella neutronica, nella microelettronica, nella propagazione ondosa), economici (nei sistemi deterministici o statistici per la descrizione di sistemi macroeconomici, o nei processi di investimento con opzioni) ecc. è notevole e destinata a crescere nel tempo.

Nel seguito esamineremo i concetti matematici che stanno a fondamento dei m. c. e le metodologie numeriche più frequentemente in uso nei processi di approssimazione, con particolare riguardo per la modellistica computazionale per problemi differenziali. Infine, verranno considerate le applicazioni di questi metodi a vari problemi studiabili tramite la trasformata di Fourier.

Fondamenti matematici dei metodi computazionali

Convergenza e stabilità dei modelli numerici

La prima fase della modellistica computazionale consiste nella sostituzione del modello matematico F(u,d)=0 con un modello numerico F_n(u_n,d_n)=0, dipendente da un parametro n il cui significato varia a seconda della famiglia di problemi considerata, ma che possiamo sempre pensare riferito alla 'dimensione' del modello numerico medesimo. In tale contesto, d_n è un'approssimazione di d, F_n una 'discretizzazione' della relazione funzionale F e u_n la soluzione numerica. La proprietà fondamentale che si richiede a un modello numerico è la convergenza, ovvero che (in un'opportuna topologia) lim_n^→_∞ u_n=u. Condizione necessaria perché ciò avvenga è che F_n traduca correttamente la legge funzionale F, ovvero che F_n(u,d)^→0 per n^→∞, essendo d un dato ammissibile per il modello matematico e u la corrispondente soluzione. Tale proprietà, detta consistenza, non è peraltro sufficiente a garantire la convergenza della soluzione numerica a quella esatta: a tale scopo serve che il modello numerico sia stabile. Al fine di definire cosa si intende con stabilità, ricordiamo che un modello matematico si dice ben posto se ammette una sola soluzione e, 'a piccole perturbazioni' dei dati, corrispondono 'variazioni controllabili' della soluzione. In altri termini, se supponiamo che d e d^* rappresentano due insiemi di dati, δd=d^*−d la loro differenza e, conseguentemente, u e u^* le soluzioni corrispondenti, e inoltre δu=u^*−u, allora il problema sarà ben posto se ∀ε>0 ∃K(ε,d) tale che se ∥δd∥〈ε, allora ∥δu∥≤K(ε,d)∥δd∥. Abbiamo indicato con lo stesso simbolo ∥∙∥ delle norme opportune (non necessariamente le stesse) per l'insieme dei dati e per quello delle soluzioni. Il numero di condizionamento K del modello è definito come:

dove l'estremo superiore viene preso sull'insieme D di tutte le perturbazioni ammissibili dei dati. Il numero K esprime dunque il massimo valore possibile del rapporto fra l'errore relativo sulla soluzione e l'errore relativo sui dati. I problemi per i quali K è dell'ordine dell'unità si dicono ben condizionati, se invece K è molto grande si diranno mal condizionati. Supponiamo che la soluzione u del problema modello si possa rappresentare come u=f(d) e analogamente la soluzione del modello numerico si possa ottenere come u_n=f_n(d_n), essendo f e f_n due opportune leggi di corrispondenza. Allora, se f è differenziabile, l'uso del teorema del valor medio consente di ottenere per K la seguente stima: K=∥f′(d)∥∥d∥/∥f(d)∥ (avendo trascurato infinitesimi di ordine superiore a ∥δd∥). Con ragionamenti del tutto analoghi possiamo associare al modello numerico un numero di condizionamento K_n=∥f′_n(d_n)∥∥d_n∥/∥f_n(d_n)∥ e definire K^*=lim_k^→_∞ sup_n≥k K_n. Il numero K^* viene detto numero di condizionamento asintotico del modello numerico. Siamo ora in grado di precisare il concetto di stabilità numerica. Dato un modello matematico ben condizionato con numero di condizionamento K, diremo che la famiglia (dipendente dal parametro n) di modelli numerici associati è stabile se K^* è dello stesso ordine di grandezza di K. In caso contrario si parlerà di modello numerico instabile. Si noti che, in particolare, la stabilità assicura la limitatezza uniforme (rispetto a n) delle soluzioni numeriche.

A titolo d'esempio consideriamo il seguente modello matematico elementare: trovare x tale che x²−2px+1=0, dove p è il dato e le soluzioni sono le due radici x_±=F(p)=p± p²− 1. Per p>1, il numero di condizionamento corrispondente è K=∣p∣/ p²− 1. Esso degenera per p^→1 in quanto le due radici sono coincidenti per p=1; tuttavia anche per p=1 il problema della ricerca delle radici è ben posto, come si vede trasformandolo nel problema equivalente: F(x,t)=x²−[(1+t²)/t]x+1=0, con t=p+ p²− 1, le cui radici x₋=t e x₊=1/t risultano coincidenti per t=1. Il cambio di parametro rimuove la singolarità presente nella precedente rappresentazione delle radici in funzione di p e il calcolo del condizionamento restituisce K≃1 per ogni valore di t. Supponendo p≫1 in modo che le radici siano ben separate, il problema è ben condizionato, ma il calcolo di x₋ attraverso la formula esplicita è instabile per via della cancellazione di cifre significative, tipica dell'aritmetica finita del calcolatore. Se si usa invece il seguente processo iterativo di Newton (adottato da quasi tutte le calcolatrici tascabili per il calcolo delle radici quadrate): x_n=x_n₋₁−(x²_n₋₁−2px_n₋₁+1)/(2x_n₋₁−2p)≡f_n(p), n≥1, si ottiene K_n=∣p∣/∣x_n−p∣. Se x₀ è scelto opportunamente allora x_n, per n^→∞, converge a una delle radici (v. oltre), e si vede che K^*=∣p∣/∣x_±−p∣=K. Trattasi dunque di un modello numerico stabile. Questo elementare esempio evidenzia come problemi ben condizionati possano essere affrontati con metodi numerici stabili o instabili.

Errore computazionale e modelli adattivi

Il modello matematico è un tentativo di legare fra loro quantità di interesse fisico attraverso relazioni matematiche, spesso semplificate rispetto alla complessità del problema originario. La soluzione u del modello matematico sarà di conseguenza diversa da quella u_f del problema fisico in esame, e tale differenza e_m=u_f−u renderà conto sia della significatività (e ragionevolezza) delle ipotesi semplificative adottate, sia dell'accuratezza con la quale le quantità fisiche reali sono state rappresentate dall'insieme d dei dati del modello. L'errore e_m è pertanto intrinseco al processo. Il modello computazionale creerà un altro errore, indicato con e_c, che esprime la distanza fra la soluzione effettivamente calcolata ū_n e u. L'errore globale e, differenza fra la reale soluzione fisica u_f e quella calcolata ū_n, risulterà dalla combinazione dei due errori, e_m e e_c. L'obiettivo della modellistica computazionale è quello di garantire un errore e_c piccolo e controllabile (affidabilità) con il minor costo computazionale possibile (efficienza). Per costo computazionale si intende la quantità di risorse (tempo di calcolo, occupazione di memoria) necessaria per calcolare la soluzione ū_n (v. numerici, calcoli, App. V; struttura: Matematica, App. V). L'affidabilità è un requisito cruciale di un modello computazionale: l'analisi mira a trovare stime dell'errore e_c (in funzione dei dati del problema e dei parametri della discretizzazione) che consentano di garantire che esso stia al di sotto di una certa soglia di precisione fissata a priori. A questo scopo è utile ricorrere ad algoritmi adattivi che adottano una procedura di retroazione (o feedback) a partire dai risultati già ottenuti per modificare i parametri della discretizzazione e migliorare la qualità della soluzione. I metodi numerici che implementano una strategia adattiva per il controllo dell'errore sono detti modelli computazionali adattivi.

Vediamo come viene generato l'errore computazionale. Come precedentemente osservato, il modello numerico deve essere implementato su calcolatore con l'ausilio di un algoritmo opportuno: fase (iv) del processo. Si generano di conseguenza nuovi errori, alcuni intrinseci all'algoritmo, altri attribuibili all'aritmetica finita di cui fa uso il calcolatore per rappresentare i numeri reali ed eseguire operazioni algebriche elementari fra di essi. Per es., se il modello matematico è rappresentato dal problema differenziale u⁽¹⁾=G(u) e per la discretizzazione della derivata si usano rapporti incrementali all'indietro (v. oltre), si ottiene come modello numerico un sistema di equazioni algebriche (lineari o non, a seconda della linearità o meno di G rispetto all'incognita u). Nel caso lineare possiamo rappresentare il sistema nella forma generale Ax=b con A matrice n×n, b termine noto, x vettore incognito (avendo indicato con n l'insieme dei nodi in cui si cerca la soluzione numerica). Anche nel caso di problemi differenziali non lineari si perviene a un sistema lineare, previa opportuna linearizzazione, utilizzando tecniche alla Newton; si ottengono sistemi lineari in innumerevoli altre circostanze, in particolare nell'approssimazione numerica di problemi differenziali alle derivate parziali. Nell'ipotesi in cui A sia non singolare, la soluzione del sistema lineare x=A⁻¹b è nota in forma esplicita attraverso la formula di Cramer, che peraltro richiede un numero di operazioni elementari superiore a n!; tale numero è proibitivo anche se n non è troppo grande (nelle applicazioni ai problemi differenziali n tipicamente è dell'ordine di 10^p per 2≤p≤6), anche per calcolatori, come gli attuali, in grado di effettuare miliardi di operazioni al secondo. Algoritmi numerici efficienti, quali l'algoritmo di fattorizzazione di Gauss, o algoritmi iterativi in sottospazi di Krylov, algoritmi multigriglia o multilivello (v. oltre), consentono di ridurre il costo sino alla soglia ottimale N≃n, introducendo tuttavia un ulteriore errore. La combinazione di tale errore con gli errori di arrotondamento dell'aritmetica finita (quest'ultimo decresce esponenzialmente con −t, dove t è il numero di cifre significative della macchina) fornisce l'errore algoritmico e_a=u_n−ū_n. L'errore del modello computazionale (e_c=u−ū_n) è la somma dell'errore numerico (e_n=u−u_n) e di quello algoritmico.

L'obiettivo ultimo dell'analisi dell'errore e_c del modello computazionale è quello di dimostrare che esso tende a zero per n^→∞. Più precisamente, si cercano stime del tipo

per un'opportuna norma ∥∙∥ che dipenderà dal problema in esame. L'esponente p (ordine di infinitesimo dell'errore rispetto a 1/n) è l'ordine del modello numerico. Nell'ipotesi ottimale in cui l'errore algoritmico e_a sia controllabile con la tolleranza desiderata, p è lo stesso ordine di infinitesimo con cui e_n tende a zero rispetto a 1/n. La tecnica dimostrativa che consente di ottenere stime dell'errore del tipo indicato è basata sull'analisi di 'buona posizione' del modello matematico e su quella di stabilità del modello numerico. Essa è detta analisi a priori, in quanto può operarsi prima di implementare effettivamente il modello numerico, e dipende in maniera implicita dal numero di condizionamento matematico K e da quello numerico K^*. La costante C(u,d) dipende dai dati del problema nonché da u e dalle sue derivate (supposto che esistano) fino a un ordine opportuno, dipendente da p. La sua quantificazione numerica è generalmente assai difficile. Di conseguenza, la stima sopra riportata è incompleta: consente di prevedere la tendenza di decadimento dell'errore per n crescenti, ma non di fornirne una quantificazione numerica accurata per n fissato. È compito dell'analisi a posteriori completare questa lacuna. Essa, sulla base della soluzione ū_n effettivamente calcolata in corrispondenza di un certo valore del parametro di discretizzazione n, e del valore del residuo r_n=F(ū_n,d) (una misura indiretta dello scostamento di ū_n da u), consente di stabilire se l'errore sia o meno al di sotto di una prestabilita tolleranza. Se ciò non è vero, un algoritmo adattivo indica come migliorare la discretizzazione (fornendo un criterio per la modifica di u) al fine di garantire una riduzione dell'errore. Nel caso elementare di un sistema lineare, se -x indica una soluzione calcolata (con un qualunque algoritmo numerico), e r=b−Ax è il residuo a essa associato, si può facilmente verificare che

,

dove ∥∙∥ indica la norma euclidea, e K(A) è il numero di condizionamento della matrice (se A è una matrice simmetrica con autovalori reali positivi, K(A)=λ_max/λ_min dove λ_max e λ_min sono rispettivamente il massimo e il minimo autovalore di A); dunque l'errore computazionale (relativo, o percentuale) è maggiorabile con il residuo (relativo) a meno del fattore K(A) che, in questo contesto, viene detto fattore di stabilità. Per problemi più complessi lo spirito è il medesimo, pur essendo in generale più difficile determinare i fattori di stabilità. I modelli computazionali adattivi combinano pertanto l'analisi a priori con quella a posteriori al fine di ottenere stime quantitativamente accurate dell'errore computazionale e_c.

I metodi numerici

Intrinseco al concetto di modello computazionale è quello di metodo numerico per la realizzazione della fase (iii) del processo che stiamo esaminando. Le componenti essenziali di un metodo numerico si possono classificare in rapporto al loro scopo, che può essere quello di: a) rappresentare in modo approssimato una funzione (o una successione finita di dati sperimentali); b) approssimare il valore numerico di un integrale; c) approssimare (localmente o globalmente) derivate di ordine arbitrario; d) approssimare soluzioni di relazioni funzionali (lineari e non) attraverso successioni il cui termine generale sia facile da ottenere e la cui velocità di convergenza sia la più elevata possibile; e) decomporre matrici di struttura generale nel prodotto di matrici più semplici, per es. triangolari, allo scopo di facilitare la risoluzione di sistemi lineari di grandi dimensioni (v. approssimazione; numerici, calcoli, App. V).

Approssimazione di funzioni

Se f:[a,b]^→R è una funzione reale nota, definita sull'intervallo [a,b] della retta reale, ci si pone spesso il problema di darne una rappresentazione approssimata, per es. tramite un polinomio, o un polinomio 'a tratti', ovvero una funzione continua che sia un polinomio su ogni sottointervallo [a_k,b_k] di una certa partizione di [a,b]. Le ragioni per le quali si cercano approssimanti polinomiali sono molteplici. Innanzitutto, i polinomi sono semplici da trattare: è immediato derivarli e integrarli, ed è facile, grazie all'algoritmo di Horner, valutarli in punti prestabiliti. È inoltre noto dal teorema di Weierstrass che ogni funzione continua può approssimarsi con ordine arbitrario di accuratezza con un polinomio di grado opportuno. Precisamente, ∀f∈C([a,b]), ∀ε>0, ∃n=n(ε), ∃p_n∈P_n tale che ∥f−p_n∥_∞〈ε, ove, qui e nel seguito, si indica con ∥g∥_∞ il massimo valore di ∣g(x)∣ nell'intervallo [a,b], g essendo una generica funzione continua.

Il teorema di Weierstrass tuttavia non è costruttivo: esso non permette di conoscere n(ε), né di costruire praticamente p_n. Esempi di risultati costruttivi sono invece forniti sia dal teorema di Taylor che dalla teoria dei polinomi ortogonali. Il primo assicura che se f∈Cⁿ⁺¹([a,b]), il polinomio Q_nf(x)=Σⁿ_k=₀f^(k)(x₀)/k!(x−x₀)^k di grado n è un'eccellente approssimazione di f e delle sue derivate in un intorno del punto x₀∈(a,b), ma sfortunatamente l'accuratezza diminuisce se x si allontana da x₀. Si parla in tal caso di approssimazione locale. Esempi di approssimazione globale sono forniti dalle serie troncate di sviluppi di f rispetto a basi di polinomi ortogonali. La famiglia {φ_k,k=0,1,...} di polinomi ortogonali in [a,b] rispetto alla funzione peso w(x)>0 è definita come segue: φ_k∈P_k e ∫^b_aφ_kφ_mw=δ_km (δ_km=0 se k∙m,δ_km=1 se k=m, è l'indice di Kronecker). Se a=−1, b=1, per w(x)=1 si ottengono i polinomi di Legendre e per w(x)=1/ 1− x² si ottengono quelli di Čebyšëv. Su un intervallo arbitrario tali definizioni si estendono in modo ovvio. Ora ˆf_k=(f,φ_k)=∫^b_afφ_kwdx è il coefficiente k-esimo di Fourier (generalizzato) di f; se la serie Σ^∞_k=₀∣ˆf_k∣² converge, allora si ha f(x)=Σ^∞_k=₀ˆf_kφ_k(x). Dunque, indicando con ∥f∥=(f,f)¹^/² la cosiddetta norma L² di f in (a,b), e, per ogni n, con f_n(x)=Σⁿ_k=₀ˆf_kφ_k(x) la serie troncata di f (si noti che f_n∈P_n), allora

o, equivalentemente,

La convergenza è tanto più rapida quanto più f è regolare, in quanto per n^→∞ si ha che ∣ˆf_n∣ tende a zero come (1/n)^p se f∈C^p([a,b]) per un certo p≥1. Tuttavia, la costruzione dei coefficienti {ˆf_k, k=0,...,n} è assai problematica e deve essere fatta in modo approssimato ricorrendo a formule di integrazione numerica gaussiane (v. oltre), in modo da preservare l'ordine di convergenza della serie.

Un approccio più semplice consiste nel sostituire f con un polinomio Π_nf di grado n che interpoli f in n+1 nodi distinti x₀,...,x_n di [a,b], ovvero Π_nf(x_j)=f(x_j), j=0,...,n. Tale polinomio si può rappresentare come Π_nf(x)=Σⁿ_j=₀f(x_j)L_j(x), L_j essendo l'unico polinomio di grado n tale che

^f(n⁺¹^)(ξ)

L_j(x_i)=δ_ij. L'errore che si genera è E_n(x)=f(x)−Π_nf(x)=--‒ w_n(x),

_n ⁽ⁿ⁺¹^)!

essendo ξ un punto opportuno di [a,b] e w_n(x)=Π(x−x_k) il cosiddet-

_k=₀

to polinomio nodale. Se i nodi sono equispaziati, si possono fornire esempi di funzioni per le quali la proprietà di convergenza uniforme lim ∥E_n∥_∞=0 non è verificata. A tal fine è possibile ricorrere a nodi op-

_n^→_∞

portunamente distribuiti, detti di tipo gaussiano: si considerano gli zeri del polinomio ortogonale φ_n₊₁, oppure le radici del polinomio (x−a)(x−b)φ′_n(x). Con tali scelte si ottiene, oltre alla convergenza uniforme, una stima dell'errore del tipo ∥E_n∥_∞≤Cn⁻^p, nell'ipotesi che f∈C^p([a,b]) (qui e nel seguito, C denota una costante positiva indipendente da n). Un'altra strategia conduce alla cosiddetta interpolazione composita: si suddivide dapprima [a,b] in sottointervalli disgiunti, di ampiezza h, e in ognuno si approssima f con una funzione continua Π_h,rf la cui restrizione su ogni intervallo è un polinomio interpolatore di grado 'basso', per es. r=1,2. In tal caso l'errore che si genera, E_h,r, verifica una disuguaglianza del tipo: ∥E^(k)_h,r∥≤Ch^r⁺¹⁻^k, k=0,1, avendo supposto f sufficientemente regolare, per es. f∈C^r⁺¹([a,b]). L'idea dell'interpolazione composita si estende senza difficoltà al caso multidimensionale ed è alla base del processo di discretizzazione degli elementi finiti (v. oltre), nonché dell'approssimazione con funzioni 'spline', nel qual caso si cercano raccordi anche per la derivata prima agli estremi dell'intervallo di integrazione.

Approssimazione di integrali

Per l'approssimazione del valore I(f)=∫^b_af(x)dx un'idea naturale è quella di calcolare I(f_n), dove f_n è un'approssimazione polinomiale di f. Prendendo per es. f_n=Π_nf, si otterrà I(f)=Σⁿ_j=₀α_jf(x_j) (dove α_j=∫^b_aL_j(x)dx), ovvero una formula di integrazione numerica in cui i punti {x_j} sono ancora detti nodi, mentre i coefficienti {α_j} sono detti pesi. Nel caso di interpolazione con nodi equispaziati si ottengono le cosiddette formule di Newton-Cotes. Otterremo invece formule di integrazione gaussiana (assai più precise nell'integrazione di funzioni polinomiali) nel caso in cui si usino nodi di interpolazione gaussiana. La valutazione dell'errore di integrazione I(f)−I(f_n) viene ereditata dalla stima del corrispondente errore E_n. Una naturale evoluzione in questa direzione si basa sull'uso di polinomi di interpolazione composita Π_h,rf, nel qual caso l'integrale su [a,b] verrà approssimato da una somma di integrali approssimati su ogni sottointervallo.

Un approccio diverso dai precedenti è alla base dei metodi di tipo Monte Carlo (v. monte carlo, metodo, App. V), dove i nodi sono scelti in modo statistico in funzione dei valori assunti da variabili casuali aventi una distribuzione di probabilità nota. Nella pratica computazionale i nodi sono ottenuti tramite un generatore di numeri casuali, e le formule che ne derivano si dicono di integrazione numerica pseudo-casuali. L'errore di integrazione su regioni dello spazio Rⁿ decresce come 1/ N (N essendo il numero di nodi), indipendentemente dalla dimensione n.

Approssimazione delle derivate di una funzione

Per approssimare in opportuni nodi i valori della derivata di una funzione f, una via naturale è ricorrere alla definizione stessa di derivata e sostituire f′(x_k) con opportuni rapporti incrementali nei nodi adiacenti. Nel caso di nodi equispaziati, indicando con h la distanza fra due nodi consecutivi e con f_k il valore f(x_k), si può approssimare f′(x_k) con (f_k₊₁−f_k)/h, ma anche con (f_k−f_k₋₁)/h, a meno di infinitesimi di ordine superiore a h. Un'accuratezza di ordine superiore si ottiene con il rapporto incrementale centrato (f_k₊₁−f_k₋₁)/2h, come si vede applicando la formula di Taylor. Naturalmente, iterando i precedenti rapporti incrementali si ottengono formule di approssimazione per derivate di ordine superiore. Questo processo, di tipo locale, è alla base dell'approssimazione alle differenze finite di problemi di Cauchy (v. oltre). Un approccio globale si ottiene invece approssimando f′(x) su un intero intervallo (a,b) con la derivata esatta di un polinomio approssimante f in (a,b) ottenuto tramite uno dei metodi precedentemente illustrati. Utilizzando per es. il polinomio Π_nf interpolante f in n+1 nodi di tipo gaussiano, si ottiene dall'analisi precedente che ∥f′−(Π_nf)′∥_∞≤Cn⁻^(p⁻¹⁾, avendo ancora assunto f∈C^p([a,b]). Questo processo è alla base dell'approssimazione di problemi ai limiti con metodi spettrali.

Iterazioni funzionali

Capita assai di frequente di dover trovare per via approssimata la soluzione di equazioni funzionali della forma F(x)=0, dove F è un sistema di equazioni, lineari o non. Una metodologia generale assai naturale consiste nel realizzare un processo iterativo della seguente forma: assegnato x₀_, per ogni k≥0 si ottiene x_k₊₁ da x_k risolvendo il problema G^k(x_k₊₁−x_k)=−F(x_k), dove G^k è un'approssimazione opportuna di F′(x_k), la matrice jacobiana di F nel 'punto' x_k. Chiameremo la matrice G^k operatore di precondizionamento, e la supporremo invertibile, di inversa H^k. Nel caso in cui F sia una trasformazione affine F(x)=Ax−b, la matrice G^k costituirà un'opportuna approssimazione della matrice A, e il processo iterativo ricomprenderà i classici metodi iterativi dell'algebra lineare numerica (di Jacobi, di Gauss-Seidel, di Richardson, del gradiente, e così via; v. numerici, calcoli, App. V). Indicato con e_k=x−x_k l'errore all'iterazione k-esima, si ha in tal caso e_k₊₁=(I−H^kA)e_k, essendo I l'identità, e per la convergenza del processo iterativo si richiederà che ϱ_k=ϱ(I−H^kA) sia minore di 1 (ϱ_k è il raggio spettrale della matrice I−H^kA). Nel caso in cui F(x)=0 sia un'equazione (o un sistema di equazioni) non lineare, il processo descritto è il paradigma di numerosi metodi classici quali il metodo delle corde, di Newton e del gradiente. L'analisi dell'errore si può fare analogamente al caso lineare. Supponendo infatti F differenziabile in un intorno della soluzione, si avrà e_k₊₁=(I−H^kF′(y_k))e_k, dove y_k è compreso fra x e x_k.

Il processo iterativo precedente comporta a ogni iterazione la risoluzione di un sistema lineare nella matrice G^k. Per la sua efficienza si richiede un compromesso fra la semplicità computazionale e la velocità di convergenza: infatti, G^k dovrebbe essere al tempo stesso di forma semplice (diagonale, triangolare, a banda, ...) e tale che lo spettro di H^kF′(y_k) sia il più compatto possibile, in modo da garantire che ρ_k (o un'opportuna norma di I−H^kF′(y_k) nel caso non lineare), sia più piccolo di 1 e più vicino possibile a 0.

Decomposizione di matrici

Per una matrice quadrata A di n righe si possono trovare due fattori, una matrice L triangolare inferiore (ovvero con elementi nulli al di sopra della diagonale principale) e una U triangolare superiore (con elementi nulli al di sotto della diagonale principale) tali che A=LU. Questa decomposizione è unica se, per es., si fissano uguali a 1 gli elementi diagonali di L (decomposizione di Gauss) o quelli di U (decomposizione di Crout). Note le matrici L e U, la risoluzione di un sistema Ax=b può ricondursi a quella di due sistemi triangolari Ly=b e Ux=y (in sequenza); ognuno dei sistemi triangolari può essere risolto con il metodo delle sostituzioni in avanti per L, all'indietro per U, con un costo computazionale di n² operazioni. Nel caso in cui A sia simmetrica con autovalori positivi, essa ammette la decomposizione (detta di Cholesky) A=HH^t, dove H è triangolare inferiore e H^t ne è la trasposta, che naturalmente risulta triangolare superiore. Conviene inoltre citare la cosiddetta decomposizione QR per la risoluzione di sistemi lineari sovradeterminati Ax=b, dove b è un vettore di m componenti, x di n componenti, e A una matrice di m righe ed n colonne, con m>n. Non esistendo una soluzione in senso classico, se ne può cercare una x^*, detta soluzione nel senso dei minimi quadrati, risolvendo il sistema n×n: A^t(Ax^*−b)=0. Il classico problema della determinazione della retta di regressione lineare che minimizza la somma dei quadrati delle distanze da una distribuzione di osservate {b_i,i=1,...,m} si formula esattamente in questo modo (in questo caso n=2 è il numero di coefficienti in grado di individuare la retta di regressione). Siano Q, R due matrici rispettivamente m×n ed n×n, l'una ortogonale e l'altra triangolare superiore, per le quali si abbia A=QR. Indicata con D la matrice diagonale Q^tQ, il sistema trasformato si può riscrivere nel modo seguente: R^tQ^t(QRx^*−b)=0, ovvero R^t(DRx^*−Q^tb)=0. Si è dunque condotti alla risoluzione in sequenza di due sistemi di struttura elementare, uno diagonale, Dy=Q^tb, l'altro triangolare, Rx^*=y.

Modellistica computazionale per problemi differenziali

La complessità dei problemi differenziali, ordinari e alle derivate parziali e la loro rilevanza nella modellistica fisico-matematica, hanno stimolato negli ultimi decenni un enorme sviluppo di metodi numerici e computazionali appropriati per la risoluzione di questi problemi.

Equazioni differenziali ordinarie

Consideriamo l'equazione differenziale ordinaria del prim'ordine y′(x)=f(x,y(x)), per x≥x₀, con un dato iniziale y(x₀)=y₀. Supporremo f lipschitziana rispetto all'argomento y in un intorno di (x₀,y₀) ovvero supporremo che esista una costante L>0 tale che ∣f(x,y₁)−f(x,y₂)∣≤L∣y₁−y₂∣. Ciò assicura che esiste una soluzione del problema, quantomeno in un intorno I=[x₀,b] del punto iniziale x₀. Passo preliminare dell'approssimazione è la suddivisione di I in n sottointervalli di ampiezza h, i cui estremi x_j=x₀+jh, con j=0,...,n, sono detti nodi. Il modello numerico genererà dei valori {u_j} approssimanti la soluzione esatta y nei nodi {x_j}. Una famiglia di metodi numerici è basata sull'idea di soddisfare l'equazione differenziale solo nei nodi, dopo aver sostituito la derivata prima con una sua conveniente approssimazione che faccia uso dei valori nodali (v. sopra). Come approssimante si può scegliere sia un rapporto incrementale, sia la derivata prima del polinomio interpolatore (in quest'ultimo caso i nodi dovranno essere non più equispaziati, ma di tipo gaussiano e h denoterà la massima distanza fra due nodi consecutivi). Un'altra strategia si basa sull'uso della formula fondamentale del calcolo integrale: y(x_j₊₁)−y(x_j)=∫_xj^xj⁺¹f(x,y(x))dx, dove l'integrale è sostituito con un'opportuna formula interpolatoria in alcuni dei nodi {x₀,x₁,...,x_j₊₁}.

In astratto, in entrambi i casi, il problema numerico assumerà la forma seguente: Σ^j_k=₀α_ku_k=hΣ^j_k=₀β_kf(x_k,u_k), dove i coefficienti {α_k} e {β_k} (non tutti necessariamente diversi da zero) caratterizzano lo schema. Possiamo ora esaminare il significato dei concetti generali di convergenza, consistenza e stabilità, precedentemente enunciati, in questo contesto. Ponendo y_j=y(x_j) per ogni j=0,...,n, lo schema è detto consistente se, posto hτ_j(h)=Σ^j_k=₀α_ky_k−hΣ^j_k=₀β_kf(x_k,y_k), si ha che τ(h)=max_j∣τ_j(h)∣^→0 per h^→0. Esempi significativi sono forniti dal metodo di Eulero in avanti (EA): u_j₊₁−u_j=hf(x_j,u_j) e dal metodo dei trapezi o di Crank-Nicolson (CN): u_j₊₁−u_j=-^h₂ [f(x_j,u_j)+f(x_j₊₁,u_j₊₁)]. Per l'analisi dell'errore di discretizzazione locale τ_j(h) si ricorre al teorema di Taylor: poiché f(x_j,y_j)=y′(x_j), si ottiene che τ(h)=O(h) per (EA), mentre τ(h)=O(h²) per (CN). Diremo che il problema numerico è convergente se la soluzione numerica {u_j} converge a quella esatta nei nodi, ovvero se ∣y(x_j)−u_j∣≤C(h) per ogni j, C(h) essendo un infinitesimo quando h^→0. Nel caso in cui un metodo converga, generalmente si ha che C(h)=Ch^p, dove p è l'ordine di infinitesimo di τ(h). Pertanto, l'analisi dell'ordine di accuratezza di un metodo numerico si può ricondurre all'analisi dell'errore di troncamento locale. Sappiamo che la consistenza non è sufficiente a garantire la convergenza, richiedendosi anche la stabilità. Quest'ultima (detta anche zero-stabilità) si traduce nella richiesta seguente: per ogni b>x₀, e per ogni h>0, sia N(h) il numero di nodi in [x₀,b], i.e. x_j=x₀+jh, con x_N(h)≤b. Se {u_j, j=1,...,N(h)} e {v_j, j=1,...,N(h)} sono le successioni generate dal metodo numerico a partire da due diversi valori iniziali differenti, u₀ e v₀, allora esiste una costante K, dipendente eventualmente da b, tale che, per ogni h sufficientemente piccolo, si abbia ∣u_j−v_j∣≤K∣u₀−v₀∣ per ogni j=1,...,N(h).

A titolo esemplificativo, consideriamo il metodo (EA). Vale l'identità y_j−u_j=(y_j−y^*_j)+(y^*_j−u_j), dove y^*_j è definito dalla relazione y^*_j−y_j₋₁=hf(x_j₋₁,y_j₋₁), ovvero è la soluzione di (EA) avendo supposto di conoscere in x_j₋₁ la soluzione esatta. Dalla definizione di τ_j(h) discende che y^*_j−y_j₋₁=hτ_j(h), quantità che esprime l'errore introdotto nel passo j-esimo. Evidentemente la quantità 'globale' di errore introdotta in [x₀,b] non potrà superare N(h)[hτ(h)], ovvero (b−x₀)τ(h). Peraltro, y^*_j−u_j=h[f(x_j₋₁,y_j₋₁)−f(x_j₋₁,u_j₋₁)] e, essendo f lipschitziana con costante L rispetto al secondo argomento, si avrà ∣y^*_j−u_j∣≤hL∣y_j₋₁−u_j₋₁∣ (relazione che può considerarsi inerente alla stabilità del metodo, in quanto esprime la variazione della soluzione numerica in rapporto a quella sui dati al generico passo j-esimo). Posto allora e_j=∣y_j−u_j∣, si ha la relazione ricorsiva e_j〈hτ(h)+hLe_j₋₁ per ogni j, la quale consente di concludere che e_j≤Cτ(h) per ogni j=1,...,N(h) con C=(exp(b)−1)/L, evidenziando, come anticipato, il contributo sinergico di stabilità e consistenza di un metodo numerico.

Il limite intrinseco del precedente concetto di zero-stabilità sta nella dipendenza (esponenziale) della costante K da b; tale dipendenza rende tale proprietà inadeguata a governare comportamenti su intervalli di integrazione grandi o addirittura illimitati. In tal caso, sarà opportuno richiedere che il metodo sia assolutamente stabile, ovvero che la soluzione {u_j} del problema modello y′(x)=λy(x) per x>0, con y(0)=1 e Reλ〈0, tenda a zero per x_j^→∞. Nel caso di (EA), si ha u_j₊₁=(1+hλ)u_j, e pertanto u_j=(1+hλ)^j; la condizione di stabilità assoluta diviene ∣1+hλ∣〈1, ovvero hλ deve appartenere al cerchio di raggio unitario e centro (−1,0) nel piano complesso. Ciò induce una limitazione su h del tipo h〈2∣Reλ∣/∣λ∣² e il metodo (EA) verrà detto condizionatamente assolutamente stabile. Al contrario, il metodo (CN)

soddisfa la relazione u_j=(¹₁⁺₋^hhλ_λ)^j per ogni j, e pertanto u_j^→0 per x_j^→+∞ incondizionatamente rispetto ad h. I metodi che godono di questa proprietà vengono detti A-stabili e sono appropriati per integrare equazioni differenziali su intervalli illimitati e anche sistemi differenziali di tipo stiff, ovvero sistemi la cui soluzione ha componenti che decadono nel tempo con dinamiche molto diverse.

Equazioni alle derivate parziali

La modellistica numerica e computazionale è di interesse primario in questo settore, la cui vastità non consente una sintesi soddisfacente in poche righe. Faremo un cenno alle più comuni metodologie di approssimazione. Se Ω⊂R^d è una regione limitata del piano (d=2) o dello spazio (d=3), molti problemi fisici si possono modellare con il seguente problema matematico: trovare una funzione u (scalare o vettoriale) dipendente dal tempo e dallo spazio tale che ogni x=(x₁,...,x_d)∈Ω e t>0 valga

formula  [

1]

con u=u₀ assegnata al tempo iniziale t=0. Il simbolo ∙/∙t esprime la derivata parziale rispetto alla variabile t (con x fissato), mentre per ogni funzione vettoriale w=w(x,t) la divergenza è definita da divw=Σ^d_i=₁∙w_i/∙x_i (dove ∙/∙x_i è la derivata parziale lungo la direzione x_i a t fissato). L'identità precedente esprime una legge di conservazione (o un sistema di leggi di conservazione nel caso vettoriale). In effetti, integrando la [1] su ogni sottoregione T di Ω, grazie al teorema della divergenza di Gauss si ottiene:

avendo indicato con Γ il bordo di T e, per ogni x∈Γ, con n=n(x) il versore, di componenti n_i, normale esterno a Γ (ovvero il vettore di modulo unitario perpendicolare al piano tangente a Γ nel punto x). Infine, f(u) è una funzione vettoriale, a d componenti f₁(u),..., f_d(u), detta flusso di u, e f(u)∙n=Σ^d_i=₁ f_i(u)n_i. La relazione precedente esprime la conservazione di u nella sottoregione T; questo significa che la variazione temporale del suo integrale ∫_T^udT è compensata dal bilancio di flusso attraverso la frontiera.

Sia {T} una partizione di Ω di elementi poligonali (triangoli o tetraedri) non sovrapponentisi. Precisamente, se prendiamo due elementi, questi possono avere in comune solo vertici, lati e facce, e la loro unione ricopre interamente Ω. Il metodo ai volumi finiti (VF) è basato sulla proprietà di conservazione, imposta su ogni sottoregione T (detta volume finito). Per ogni coppia di volumi finiti adiacenti, T_i e T_j, detta Γ_ij l'interfaccia fra T_i e T_j, i flussi normali su Γ_ij sono deputati a stabilire le relazioni di interdipendenza fra i valori delle incognite uⁱ=u_∣Ti e u^j=u_∣Tj (generalmente supponendo uⁱ costante su T_i, per ogni i). Tipicamente avremo:

dove la somma è estesa a tutti gli indici j per i quali T_j è adiacente a T_i, mentre f_ap(uⁱ,u^j) è una conveniente approssimazione del flusso normale f(u)∙n su Γ_ij.

Il metodo delle differenze finite (DF) si basa invece sulla sostituzione delle derivate spaziali ∙/∙x_i in [1] con opportuni rapporti incrementali in nodi allineati lungo la i-esima direzione coordinata (analogamente a quanto fatto per approssimare altre derivate precedentemente). Infine il metodo degli elementi finiti (EF) viene derivato dalla forma [1], supponendo che u sia approssimata con una funzione u_h la cui restrizione a ogni T (stavolta detto elemento finito) sia un polinomio di grado 1 (o più elevato), continuo sulle interfacce, e che sia soluzione del problema

formula  [

2]

essendo v_h una funzione (della sola x) polinomiale su ogni T dello stesso grado di u_h, f_h(u_h) un'opportuna approssimazione di f(u_h) e g dovuta all'eventuale contributo del flusso normale (qualora venga assegnato) sulla frontiera fisica ∙Ω della regione Ω. Per flussi f_h(u_h) di forma complessa, gli integrali richiederebbero di essere approssimati numericamente (v. sopra). Nelle notazioni precedenti, h indica la massima lunghezza dei lati dei triangoli T, così che u_h^→u per h^→0. L'approssimazione agli elementi finiti si ispira alla cosiddetta formulazione debole del problema [1], formulazione che (nel caso di problemi stazionari e simmetrici) esprime a livello discreto il principio dei lavori virtuali, per cui le v_h sono le approssimanti dei cosiddetti spostamenti virtuali. Risulta evidente che, per l'effettiva risoluzione dei problemi sopra riportati, converrà discretizzare anche la derivata temporale, utilizzando per es. schemi alle differenze finite (esplicite o implicite) o lo stesso metodo agli elementi finiti. Nel caso implicito l'equazione [2] genererà per ogni livello temporale un sistema di equazioni per la cui soluzione si possono usare le tecniche numeriche illustrate prima.

Strategie multi-livello

Come si è visto in molte situazioni, per l'approssimazione di problemi differenziali, siano essi ordinari o alle derivate parziali, si è ricondotti alla soluzione di sistemi lineari della forma A_hx_h=f_h, dove x_h indica il vettore delle incognite nodali di una griglia di calcolo la cui ampiezza caratteristica è h, mentre f_h e A_h indicano rispettivamente il termine noto e la matrice associati al sistema. Se si usa un metodo iterativo (quale il metodo di Jacobi, o quello di Gauss-Seidel) si osserva che poche iterazioni sono sufficienti per abbattere le alte frequenze dell'errore e^k=x^k_h−x_h, mentre per la riduzione delle basse frequenze servirebbero moltissime iterazioni. Allo scopo di accelerare la convergenza si può ricorrere a un problema ausiliario A_Hx_H=f_H, che possiamo immaginare associato alla discretizzazione dello stesso problema, ma su una griglia più rada di ampiezza caratteristica H>h. A ogni vettore v_H composto da valori nodali sulla griglia 'rada' possiamo associare un vettore v_h=I_hv_H composto da valori nodali sulla griglia 'fine' originaria. Tipicamente I_h è un processo di interpolazione rappresentabile con una matrice rettangolare. Indichiamo con I^t_h la matrice trasposta di I_h, che rappresenta dunque il processo di restrizione dalla griglia fine alla griglia rada. Indichiamo con Q_H la matrice la cui inversa sia Q⁻¹_H=I_hA⁻¹_HI^t_h, e con Q_h la matrice A_h o un suo conveniente precondizionatore (v. sopra). Per la risoluzione del sistema originario si può usare il metodo iterativo che illustriamo di seguito. Se u^k_h è nota (per k≥0), si definisca u_h^k⁺¹^/² tramite la soluzione del sistema lineare (sulla griglia rada)

e quindi si definisca u_h^k⁺¹ come soluzione del sistema (sulla griglia fine)

Combinando i due processi si trova che

ovvero u_h^k⁺¹ è il risultato di una singola iterazione di Richardson sul problema originario, dove si introduca il precondizionatore P tale che P⁻¹=Q⁻¹_H+Q⁻¹_h−Q⁻¹_hA_hQ⁻¹_H. Si ritrova in questo modo il metodo multigriglia nella sua versione più semplice (a due livelli). I metodi a più livelli sono ottimali dal punto di vista della complessità computazionale, in quanto per la risoluzione del sistema originario richiedono un numero di operazioni proporzionale al numero di incognite (ovvero al numero di righe della matrice A_h). Una versione ridotta del metodo multilivello più adatta a calcolatori di tipo multi-processore si ricava sostituendo P con P_par, dove P⁻¹_par=Q⁻¹_H+Q⁻¹_h si ottiene trascurando l'interazione non lineare fra Q⁻¹_H e Q⁻¹_h. I cosiddetti metodi di decomposizione per sottodomini (o sottoregioni), introdotti a metà degli anni Ottanta per la risoluzione parallela di problemi differenziali, possono essere formulati come esempi notevoli di tali procedure.

bibliografia

K.E. Atkinson, An introduction to numerical analysis, New York 1989.

G.H. Golub, C.F. Van Loan, Matrix computation, Baltimore (Md.)-London 1989.

J.D. Lambert, Numerical methods for ordinary differential systems. Initial value problem, Chichester 1991.

A. Quarteroni, A. Valli, Numerical approximation of partial differential equations, Berlin 1994.

K. Eriksson et al., Computational differential equations, Cambridge 1996.

Y. Saad, Iterative methods for sparse linear systems, Boston (Mass.) 1996.

B. Smith, P. Bjørstad, W. Gropp, Domain decomposition, Cambridge 1997.

A. Quarteroni, R. Sacco, F. Saleri, Matematica numerica, Milano 1998.

Applicazioni dell'analisi armonica

La trasformata di Fourier è il principale strumento matematico della teoria dei segnali (v. anche segnale, App. V). Nelle applicazioni, la sua importanza dipende dal fatto che il modello ondulatorio è utilizzato per descrivere vaste classi di fenomeni fisici, tra cui le radiazioni dello spettro elettromagnetico e il suono. Il corrispondente modello computazionale si basa su un'approssimazione detta trasformata di Fourier discreta e sull'esistenza di un algoritmo che permette un rapido calcolo, la trasformata rapida di Fourier. In ipotesi alquanto generali (v. fourier, jean-baptiste-joseph: Serie di Fourier, XV), una funzione periodica di periodo T a valori complessi può essere decomposta tramite la serie di Fourier, come somma infinita di armoniche f(t)=Σ⁺^∞ c_n e²^πi-nt_T dove i

_n=₋_∞

numeri c_n sono i coefficienti di Fourier complessi (i è l'unità immaginaria i²=−1) definiti nel modo seguente

Questa decomposizione permette d'identificare univocamente f(t) con la successione di numeri T e c_n e di ottenere f(t) a partire da essi. Al variare di n, le frequenze n/T delle armoniche costituiscono lo spettro discreto e i coefficienti di Fourier, detti anche ampiezze o fattori di pesaggio delle armoniche, tendono a zero per n^→∞. Una funzione non periodica g(t) di variabile reale può essere intesa come una funzione di periodo infinito. In condizioni alquanto generali e usualmente verificate nella pratica può essere definita la trasformata o integrale di Fourier di g(t):

formula

[1]

Vale la formula di inversione, analoga alla somma infinita ottenuta per le funzioni periodiche,

in cui le armoniche hanno come frequenza un qualsivoglia numero reale ω (spettro continuo) e come fattore di pesaggio ĝ(ω), che tende a zero al tendere di ω all'infinito. Se definiamo g_a(t)=g(at) allora la funzione g_a(t) risulta una contrazione o una dilatazione della funzione g(t) a seconda che il numero reale positivo a sia minore o maggiore di 1. Tra le proprietà della trasformata di Fourier si ha che ĝ_a(ω)=(1/a)ĝ(ω/a) e quindi, salvo il fattore 1/a, la trasformata di una contrazione o dilatazione risulta essere rispettivamente la dilatazione o la contrazione della trasformata ĝ.

Ricordiamo che l'apparente diversità tra il caso periodico e non periodico scompare quando si considera la trasformata di Fourier da un punto di vista astratto su un gruppo abeliano localmente compatto. Il calcolo della trasformata di Fourier non è implementabile su un calcolatore, che riesce a trattare solamente un numero finito di dati. La trasformata di Fourier discreta approssima la trasformata di Fourier e richiede solo un numero finito di addizioni e moltiplicazioni; la sua formula comparve esplicitamente per la prima volta nel 1754 in un lavoro del matematico A.-C. Clairaut, che riprendeva una formula simile del 1750 dovuta a L. Eulero, e a cui fecero seguito due lavori di J.L. Lagrange. I problemi trattati includevano la propagazione del suono in un mezzo elastico e la modellizzazione del movimento apparente del Sole rispetto alla Terra. Di una funzione h(t), rappresentabile sull'intervallo [0,T] da una serie trigonometrica finita

si possono calcolare i coefficienti C_n se sono noti N campioni uniformemente distribuiti h_k=h(-^kT_N), k=0,...,N−1, mediante la

formula [

2]

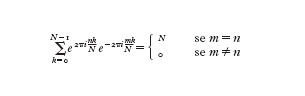
che può essere verificata utilizzando le relazioni di ortogonalità

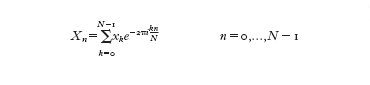
La trasformata di Fourier discreta di una funzione x(t) (dove 0≤t≤T) è definita nel modo seguente

formula [

3]

dove X_n=X(-ⁿ_T) e x_k=x(-^kT_N). Tale formula è simile alla [2] e inoltre vale la formula di inversione:

Se x(t) è definita su un intervallo infinito, per applicare la [3] dopo il campionamento bisogna effettuare un troncamento su un qualche intervallo [0,T]. La bontà dell'approssimazione dipende dalla funzione in esame e può essere migliorata aumentando il numero dei campioni e l'intervallo di troncamento. C.F. Gauss, che era a conoscenza dei lavori di Lagrange (mentre era studente a Göttingen, dal 1795 al 1798, prese in prestito dalla biblioteca i libri che li riportavano), descrisse nell'opera Theoria interpolationis methodo nova tractata, scritta probabilmente nel 1805, un metodo che "grandemente riduce la laboriosità del calcolo" della formula [2] e lo applicò alla determinazione dell'orbita di un asteroide individuato nel 1802 e chiamato Pallade. Il trattato venne pubblicato nel 1866, undici anni dopo la morte di Gauss, ma il metodo introdotto non fu notato e solo nel 1977 H.H. Goldstine richiamò l'attenzione su di esso. Nel frattempo, nel 1965, J.W. Cooley e J.W. Tukey avevano riscoperto tale metodo e lo avevano chiamato trasformata rapida di Fourier (FFT, Fast Fourier Transform): si tratta di un algoritmo che, sfruttando le simmetrie delle potenze della radice N-esima dell'unità W=e⁻²^πi_N-‒, calcola la trasformata di Fourier discreta di N dati complessi x_k (dove k=0,...,N−1) mediante un numero di operazioni proporzionale a N log₂N, se N è una potenza di 2. Il calcolo diretto della [3] richiede N² moltiplicazioni, le quali influenzano il tempo di calcolo in modo predominante, ed N(N−1) addizioni. Per grandi valori di N, il vantaggio della trasformata rapida di Fourier sul metodo diretto è evidente: per esempio se N=2¹⁰=1024 allora N²=1048576 mentre N log₂N=10240. Supponendo che N sia il prodotto di due interi N₁ e N₂, l'idea di Gauss fu di scrivere n=N₁n₁+n₂ e k=N₂k₂+k₁, dove n₂,k₂=0,...,N₁−1 e n₁,k₁=0,...,N₂−1. Usando l'identità W^N=1 e ponendo X_n=X(n₁,n₂), come pure x_k=x(k₁,k₂), la [3] può essere scritta:

Il calcolo di un singolo X_n richiede N₁+N₂ moltiplicazioni, N₁ per la somma più interna e N₂ per quella più esterna; in totale sono necessarie N(N₁+N₂) moltiplicazioni. Gauss, dopo aver applicato il metodo all'orbita di Pallade con N=12, N₁=3 e N₂=4, annota che l'algoritmo può essere generalizzato al caso in cui N abbia più di due fattori. In questo caso Cooley e Tukey quantificano la complessità computazionale in N Σ_iN_i, che diventa N log₂N nel caso N sia una potenza di 2. La trasformata rapida di Fourier ha segnato una svolta nell'elaborazione numerica dei segnali, la cui importanza viene messa in evidenza dalle applicazioni che seguono.

Trasformata ottica. - Ogni punto di un'apertura posta sul cammino di un fascio di raggi luminosi diventa sorgente di luce che viene diffusa in tutte le direzioni. Disponendo di un fascio di luce parallelo e monocromatico, per osservare il fenomeno di diffrazione all'infinito o diffrazione di Fraunhofer, occorre una fenditura dalle dimensioni paragonabili alla lunghezza d'onda del fascio, quindi dell'ordine di grandezza del μm. In tal caso su uno schermo che intercetti i raggi diffusi, posto a distanza molto grande rispetto alle dimensioni lineari del sistema diffrangente, viene a disegnarsi una figura di diffrazione chiamata trasformata ottica della fenditura. La trasformata ottica si discosta nettamente dalla forma della fenditura. Infatti, assunta come unità di misura la lunghezza d'onda del fascio, l'intensità dei raggi luminosi che colpiscono lo schermo risulta proporzionale al quadrato del modulo della trasformata di Fourier della funzione che vale 1 nei punti della fenditura e 0 altrove. Se la fenditura è un cerchio, sullo schermo compare una macchia circolare brillante circondata da anelli, detti anelli di Airy, alternativamente scuri e chiari, questi ultimi di intensità rapidamente decrescente. Le dimensioni della fenditura sono critiche: se sono molto più grandi della lunghezza d'onda della luce utilizzata, il fenomeno di diffrazione diventa impercettibile a causa della contrazione; se sono molto più piccole il massimo centrale diventa molto esteso e debole per la dilatazione della trasformata di Fourier (v. anche informazioni, trattamento ottico delle, App. IV).

Cristallografia. - Il fenomeno di diffrazione all'infinito è utilizzato in cristallografia come mezzo di indagine sulla struttura della materia. Benché i cristalli sembrino una rara eccezione, la maggior parte dei solidi in natura sono cristalli o policristalli. Nel 1671 il medico danese N. Steno, tagliando cristalli di quarzo, notò che gli angoli solidi formati dalle facce erano sempre gli stessi. Verso la fine del 18° sec. si fece strada l'idea che i cristalli fossero formati dalla ripetizione regolare di un blocco di base chiamato cella elementare. La conferma si ebbe nel 1912, quando M. von Laue condusse un esperimento per stabilire se i cristalli dessero luogo al fenomeno della diffrazione nel caso la radiazione incidente avesse lunghezza d'onda paragonabile alla distanza tra gli atomi del cristallo, circa 10⁻⁸ cm. Egli usò con successo i raggi X, benché all'epoca non si sapesse se questi ultimi avessero la lunghezza d'onda richiesta: sulla lastra fotografica utilizzata per intercettare i raggi in uscita dal cristallo comparvero macchie isolate. La disposizione spaziale degli atomi di un cristallo è individuata dalla densità elettronica, il cui valore dà il numero degli elettroni per volume unitario e i cui massimi corrispondono alla posizione dei nuclei degli atomi. Poiché un cristallo è costituito da copie della cella elementare ripetute periodicamente nelle tre dimensioni spaziali, la densità elettronica è una funzione periodica, calcolabile tramite la sua serie di Fourier se sono noti i coefficienti di Fourier. Durante l'esperimento di diffrazione si varia l'orientamento del cristallo rispetto alla direzione del fascio incidente per portare in condizioni di diffrazione i diversi piani reticolari e ottenere tutti i possibili picchi di diffrazione. Di ogni picco si misura l'intensità e l'angolo che il fascio diffratto forma con il fascio incidente. Assunta come unità di misura la lunghezza d'onda λ dei raggi X utilizzati, il modello matematico consente di associare a ogni picco di intensità, rappresentato da un nodo di un reticolo tridimensionale interno alla sfera di raggio 2/λ, uno dei coefficienti di Fourier. L'intensità misurata determina il modulo del coefficiente, ma viene persa la fase che permetterebbe di ricostruire la densità elettronica con dettagli dell'ordine di grandezza di λ. Nel caso di strutture cristalline semplici può accadere che siano poche le possibilità per la distribuzione degli atomi nella cella elementare. In questi casi, simulando numericamente l'esperimento di diffrazione e confrontando i risultati con i dati sperimentali si può individuare l'unica configurazione possibile.

All'inizio degli anni Cinquanta J. Karle e H. Hauptman introdussero i metodi diretti, un tipo di procedure con cui è possibile assegnare probabilisticamente le fasi; tale classe di metodi ha generalmente trasformato in routine la determinazione di strutture aventi fino a qualche centinaio di atomi nella cella elementare. Tuttavia, poiché la probabilità con cui si assegnano le fasi diminuisce con l'aumentare del numero degli atomi nella cella elementare, resta aperto il problema di rafforzare le tecniche esistenti nel caso di strutture cristalline più complesse. Il metodo degli atomi pesanti, utilizzato da M.F. Perutz per la determinazione della complessa struttura dell'emoglobina nel 1960, consiste nel modificare la molecola introducendo in varie posizioni atomi pesanti come quelli di mercurio, oro o platino. Tale intervento produce cambiamenti significativi nelle intensità dello spettro di diffrazione, permettendo di ottenere informazioni sulla fase. Anche per la determinazione, avvenuta nel 1953, della struttura a doppia elica del DNA da parte di J.D. Watson e F.H.C. Crick, la chiave fu lo spettro di diffrazione ottenuto dalla cristallografa R.E. Franklin. Tuttavia, non avendo il DNA una struttura periodica nelle tre dimensioni, la densità elettronica non ha spettro discreto e il problema della fase, che andrebbe attribuita su un continuo, risulta insormontabile. Il metodo utilizzato in questi casi consiste nel fare un'ipotesi di struttura, calcolarne la trasformata di Fourier e confrontarla con i dati sperimentali.

TAC e RMI. - Le tecniche della tomografia assiale computerizzata (TAC) e della risonanza magnetica per immagini (RMI), la cui sperimentazione risale agli anni Sessanta e Settanta rispettivamente, hanno rivoluzionato la radiologia diagnostica classica (v. radiologia medica, App. V). Quest'ultima riesce a distinguere efficacemente soltanto tra aria, tessuti molli e ossa in virtù della diversità con cui questi elementi assorbono i raggi X; un'ulteriore limitazione è dovuta alla sovrapposizione delle immagini, in quanto una comune radiografia è originata da tutto lo spessore della struttura irradiata. La TAC e la RMI superano questi inconvenienti e producono una descrizione numerica della densità del tessuto corporeo che il medico esamina attraverso lo schermo di un computer o una fotografia dello stesso. Il modello matematico della TAC è la trasformata di Radon, proposta per la sua applicazione in radiologia nel 1963 dal fisico statunitense A.M. Cormack. Lo schema di base di questa tecnica diagnostica fu messo a punto nel 1972 dall'ingegnere inglese G.N. Hounsfield, che divise con Cormack il premio Nobel per la medicina nel 1979. Si considera una sorgente di raggi X che ruota attorno alla sezione piana, da esaminare, perpendicolare all'asse del corpo. La sorgente si ferma in posizioni equidistanti sul cerchio che descrive attorno al paziente, per emettere pennelli di centinaia di sottili fasci di raggi, tutti giacenti nel piano della sezione in esame, e di cui viene misurata l'attenuazione. Sono quindi note l'intensità I₀ di un raggio L prima di entrare nel corpo (intensità incidente) e l'intensità I dello stesso raggio dopo averlo lasciato (intensità trasmessa) e quindi anche l'integrale di linea ∫_Lϱdt, detto radiografia della densità corporea ϱ(x,y) (normalizzata), stante la formula log(I/I₀)=∫_Lϱdt. La trasformazione che associa a una funzione, al variare di L, gli integrali di linea sopra definiti è chiamata trasformata di Radon. Fu introdotta nel 1917 da J. Radon, al quale si deve anche una formula di inversione esplicita che permette di determinare la densità ϱ a partire dalle radiografie. Tuttavia la TAC utilizza la formula di inversione della trasformata di Fourier, più comoda per il calcolo automatico, essendo possibile esprimere le radiografie mediante questa trasformata. La TAC è utilizzata anche a fini industriali per ispezionare dettagliatamente parti complesse o critiche in motori a reazione, turbine o reattori nucleari.

La risonanza magnetica per immagini comparve tra gli esami clinici negli anni Ottanta. Essa segnala il contenuto di idrogeno (e quindi di acqua) nei tessuti, contenuto che varia da tessuto a tessuto e da tessuto sano a tessuto malato. Fu P.C. Lauterbur a ottenere nel 1973 la prima mappa bidimensionale di due piccole provette piene d'acqua e nel 1976 si ebbe la prima immagine di un tumore in un animale vivo. I nuclei degli atomi, essendo carichi elettricamente e dotati di un rapido movimento di rotazione attorno a se stessi, generano un debole campo magnetico espresso da un vettore, detto momento magnetico o dipolo. Se viene imposto dall'esterno un campo magnetico B₀ (campo magnetico statico), i dipoli si orientano in direzione parallela a B₀ o antiparallela. Alla temperatura ambiente, essendo i nuclei con momento magnetico parallelo a B₀ in numero leggermente superiore a quelli con momento magnetico antiparallelo, è rilevabile (a livello macroscopico) un campo magnetico M₀, diretto come B₀ e di intensità proporzionale a quella di B₀ e al numero dei nuclei presenti nel campione. Poiché ogni nucleo è dotato di una frequenza di risonanza o frequenza di Larmor ω₀, che dipende solo dal tipo di nucleo e dall'intensità del campo magnetico statico, per osservare una determinata specie nucleare si applica un campo a radiofrequenze (RF) ruotante nel piano perpendicolare a B₀ con frequenza pari alla frequenza di Larmor. Si nota allora una forte interazione (risonanza): il campo magnetico M₀ si sposta in una posizione M e, al cessare dell'impulso RF, torna alla posizione di equilibrio M₀ (processo di rilassamento), ruotandovi attorno (moto di precessione), come avviene a una trottola in movimento se viene spostato il suo asse dalla verticale. Il campo M, variando nel tempo, genera una debole forza elettromotrice che, amplificata e visualizzata mediante un oscilloscopio, dà il cosiddetto segnale di precessione libera o segnale RM.

In condizioni ideali, a meno di una costante di proporzionalità, il segnale RM è espresso da s(t)=M₀e⁻⁻^t_Te^iω⁰^t. Esso contiene solo la frequenza di risonanza e presenta un decadimento esponenziale regolato da una costante T, detta tempo di rilassamento. Se i nuclei dell'idrogeno (che sono costituiti da un unico protone), localizzati in prossimità di punti diversi A e B, risuonassero a frequenze diverse ω_A e ω_B, il segnale RM conterrebbe dette frequenze con peso proporzionale alla densità protonica σ_A e σ_B (purché l'impulso RF venga scelto in modo da contenere ω_A e ω_B) e sarebbe espresso da s(t)=M₀(σ_Ae^iωAt+σ_Be^iωBt) trascurando il decadimento esponenziale. L'analisi di Fourier permette allora di individuare i fattori di pesaggio σ_A e σ_B. Per far sì che i nuclei d'idrogeno nelle varie parti del campione risuonino a frequenze diverse si sovraimpone a B₀ un campo magnetico, detto gradiente di campo, diretto come B₀ e di intensità variabile, dipendente linearmente dalle coordinate spaziali. Applicando impulsi opportuni si può conoscere la trasformata di Fourier della densità protonica in un numero di punti sufficiente a determinare, mediante la trasformata rapida di Fourier, la densità protonica stessa σ(x,y,z) con la precisione desiderata. La RMI, essendo interamente elettronica, è sufficientemente veloce da dare immagini non sfocate del cuore, mentre la TAC cardiovascolare è effettuata solo sperimentalmente, con macchine prototipo aventi tempi di osservazione brevi e velocità di scansione elevate, al fine di 'congelare' il battito cardiaco.

Spettroscopia RM. - La nube di elettroni che circonda il nucleo causa l'abbassamento della frequenza di risonanza (spostamento chimico), osservato per la prima volta nel 1949 da W.D. Knight nei metalli e nel 1950 da J.T. Arnold nei liquidi. Il segnale RM può quindi fornire indicazioni sulla distribuzione degli elettroni in una molecola e conseguentemente sulla composizione e struttura della stessa. La spettroscopia RM permette di caratterizzare la struttura di composti chimici semplici o complessi come proteine, polisaccaridi, lipidi, acidi nucleici, di cui è spesso arduo ottenere cristalli (per questo motivo a tali composti non è possibile applicare le tecniche illustrate sopra); essa è utilizzata anche per analizzare in vivo sistemi metabolici complicati.

Radioastronomia. - L'atmosfera terrestre blocca la radiazione elettromagnetica proveniente dallo spazio in tutte le lunghezze d'onda e funziona in questo modo come un filtro. Il filtro atmosferico presenta due finestre attraverso cui si può osservare dalla Terra la radiazione cosmica: la finestra ottica e la finestra radio, quest'ultima riguardante le lunghezze d'onda che vanno dal millimetro a venti metri circa. Il primo a intercettare casualmente, agli inizi degli anni Trenta, onde radio provenienti dalle regioni centrali della Via Lattea, fu l'ingegnere K. Jansky mentre lavorava, alle dipendenze della compagnia dei telefoni statunitense, per scoprire l'origine dei rumori presenti nel radiotelefono transatlantico da poco inaugurato. La radioastronomia ricevette nuovo impulso dalle ricerche sul radar, una delle più importanti innovazioni tecniche della Seconda guerra mondiale. Un radiotelescopio consiste di un paraboloide, detto antenna, che può essere metallo solido o una fitta rete metallica, montato in modo da poter essere puntato in ogni direzione del cielo. Esso intercetta la radiazione che arriva parallelamente all'asse dell'antenna e la riflette in un punto detto fuoco, non diversamente da un telescopio ottico a specchio riflettente. Il principio che descrive la formazione dell'immagine è quello di diffrazione all'infinito, con il disco del paraboloide che funge da apertura. L'immagine è dunque una figura di diffrazione. Il potere risolutivo misura la capacità di produrre immagini distinte di due oggetti vicini ed è proporzionale a λ/D, dove λ è la lunghezza d'onda e D la misura dell'apertura. Poiché le onde radio sono centinaia di migliaia di volte più lunghe delle onde luminose, le possibilità della radioastronomia sembrerebbero fortemente limitate, se non fosse per la tecnica dell'interferometria, di cui fu pioniere il fisico inglese M. Ryle. Questa tecnica, che richiede anche solo due paraboloidi mobili su rotaia e tempi di osservazione più lunghi durante i quali si deve poter supporre che la sorgente sia stabile, somma i due segnali a disposizione e ottiene un terzo segnale avente una struttura fine dovuta alle frange di interferenza. Il modello matematico, detto sintesi d'apertura, descrive il fenomeno tramite due funzioni, la visibilità complessa e la brillanza del cielo, l'una trasformata di Fourier dell'altra. Poiché la visibilità complessa può essere calcolata a partire dalle misure effettuate durante le osservazioni, la trasformata rapida di Fourier permette di risalire alla brillanza del cielo. La risoluzione è pari a quella di un paraboloide di diametro uguale alla distanza tra i due effettivamente utilizzati.

Analisi e sintesi del suono. - Attorno al 1860 lo scienziato tedesco H. Helmholtz ebbe l'idea di applicare il metodo di Fourier all'analisi del suono. Un suono semplice è quello emesso da un diapason. Se si tralascia attacco e decadimento, durante il sostenuto le molecole dell'aria nelle immediate vicinanze (subendo una compressione seguita da una rarefazione e così via) oscillano periodicamente attorno alla posizione di riposo. La formula che descrive il movimento di ognuna di esse al variare del tempo t è y=D sen(2πνt), dove ν è la frequenza o numero di oscillazioni al secondo e D è l'ampiezza dell'oscillazione. Ogni suono può essere convertito in corrente elettrica e la sua forma d'onda visualizzata mediante un oscilloscopio. L'analisi armonica consente di esprimere un certo suono come somma di suoni periodici semplici (armoniche), le cui frequenze sono multipli interi della frequenza più bassa detta fondamentale. Il procedimento per ottenere questa decomposizione può essere realizzato con reti elettriche su un calcolatore. L'avvento dell'elettronica ha reso possibile anche la generazione di suoni elettrici, i quali necessitano di amplificatore e di cassa di risonanza in quanto non vi è all'origine alcun tipo di suono acustico. I pionieri in questo campo iniziarono a operare intorno al 1920, con la costruzione di strumenti che permettevano di variare la vibrazione modificando gli elementi di un circuito oscillante; la successiva introduzione dei calcolatori ha permesso di ottenere la sintesi digitale del suono. I moderni sintetizzatori, strumenti costituiti esclusivamente da calcolatori, oscillatori digitali e non, circuiti analogici e amplificatori, sono un elemento caratteristico della musica contemporanea. Essi consentono la creazione di suoni completamente nuovi e modifiche ed estensioni, non facilmente realizzabili altrimenti, di suoni musicali naturali; inoltre permettono al compositore di ascoltare in tempo reale il brano composto. Fra i primi a usarli sistematicamente per effettuare la sintesi digitale del suono si possono citare, negli Stati Uniti, M.W. Mathews (verso la fine degli anni Sessanta) e, in Italia, P. Grossi, G. Di Giugno e G.B. Debiasi.

bibliografia

G.H. Stout, L.J. Jensen, X-ray structure determination. A practical guide, New York 1968, 1989².

H. H. Goldstine, A history of numerical analysis from the 16th through the 19th century, Berlin 1977.

J.D. Dunitz, X-ray analysis and structure of organic molecules, Ithaca (N.Y.) 1979.

T. Heideman et al., Gauss and the history of the fast Fourier transform, in Archive for history of exact science, 1985, 34, pp. 265-75.

R.N. Bracewell, The Fourier transform and its applications, New York 1986.

C. Ruffato et al., RMN in medicina, Padova 1986.

A.R. Thompson et al., Interferometry and synthesis in radioastronomy, New York 1986.

E.O. Brigham, The fast Fourier transform and its applications, Englewood Cliffs (N.J.) 1988.

J.S. Walker, Fourier analysis, Oxford 1988.

K.H. Hausser, H.R. Kalbitzer, NMR in medicine and biology, Berlin 1991.

C. Giacovazzo et al., Fundamental of crystallography, Oxford 1992.

Basic principles and clinical applications of helical scan, ed. K. Kimura, S. Koga, Tokyo 1993.

J.C. Roederer, Introduction to the physics and psychophysics of music, Berlin 1995.

E. Prestini, Applicazioni dell'analisi armonica, Milano 1996.

Musical signal processing, ed. C. Road et al., Lisse 1997.