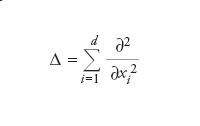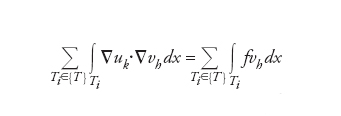metodo agli elementi finiti
metodo agli elementi finiti
Metodo numerico per l’approssimazione della soluzione di un’equazione (o di un sistema di equazioni) alle derivate parziali. Sia Ω un sottoinsieme limitato di ℝδ, con d=2,3, e su tale dominio consideriamo, per es., il seguente problema: trovare una funzione u dipendente dalla variabile spaziale, tale che per ogni x=(x1,…,xδ)∈Ω valga −Δu= f con un’opportuna condizione al contorno, per es., una condizione di Dirichlet omogenea per cui u=0 per ogni x∈Ω. Si ricorda che
è l’operatore di Laplace. Sia {T} una partizione di Ω in elementi poligonali (triangoli o quadrilateri per d=2, tetraedri o esaedri per d=3) non sovrapponentisi, ovvero tali che due elementi distinti di {T} possono avere in comune solo lati, vertici e facce e la loro unione ricopre interamente Ω. Se gli elementi di {T} sono triangoli o tetraedri, approssimare la soluzione u del problema differenziale dato mediante il metodo agli elementi finiti ℙκ vuol dire cercare una funzione uη che sia continua su Ω, che ristretta al generico elemento Tι di {T} sia un polinomio di grado k e che sia soluzione del problema
dove vη è una generica funzione continua su Ω, polinomiale su ogni elemento dello stesso grado di uη e soddisfacente le stesse condizioni al bordo di uη. Il parametro h indica la massima lunghezza dei lati degli elementi di {T}. Gli elementi finiti ℙκ sono detti di tipo lagrangiano in quanto la base di polinomi scelta per la rappresentazione della soluzione numerica è fornita dai polinomi di Lagrange. Sotto opportune ipotesi di regolarità della partizione {T} si ha che uη→u per h→0, ossia è garantita la convergenza della soluzione numerica alla soluzione del problema matematico.