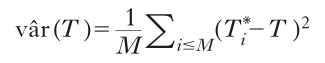bootstrap, metodo

bootstrap, metodo

Metodo ideato da B. Efron nel 1979 allo scopo di stimare caratteristiche della distribuzione di probabilità di uno stimatore o, più in generale, di una statistica di interesse. La tecnica si basa sull’assunto che, se i dati sono il risultato di un campionamento casuale, la distribuzione di uno stimatore (o una sua qualche caratteristica, come la media, la varianza o i quantili) può essere vista come una funzione dipendente dalla legge di probabilità della popolazione da cui provengono le osservazioni campionarie. Essendo quest’ultima sconosciuta, si sostituisce a essa una sua approssimazione basata sui dati campionari. Nella sua formulazione classica, tale approssimazione è ottenuta considerando il campione stesso come una approssimazione dell’intera popolazione. Ciò equivale a generare nuovi campioni estratti casualmente da quello originario, usando la funzione di distribuzione empirica. In corrispondenza di ciascun campione b. si ottiene un nuovo valore dello stimatore o della statistica. La distribuzione dello stimatore, al variare dei possibili campioni b., è usata per valutare la distribuzione desiderata. I campioni b. possono essere della stessa dimensione n del campione originario, oppure di una dimensione inferiore; in tal caso si parla di sottocampionamento (subsampling) o di b. m su n (m out of n bootstrap). Questo metodo di ricampionamento è più robusto, nel senso che fornisce risultati affidabili anche in molti casi nei quali il b. classico non funziona correttamente. Per l’implementazione del metodo b. si usano spesso procedure Monte Carlo (➔ Monte Carlo, metodo): non essendo in grado di calcolare analiticamente le caratteristiche della distribuzione dello stimatore b., queste vengono approssimate grazie a numerose ripetizioni dell’operazione di ricampionamento. Per es., un algoritmo di tipo Monte Carlo per la stima b. della varianza di (T=med (X₁, ..., X_n)−θ), dove med (X₁, ..., X_n) è la mediana campionaria e θ è la mediana della popolazione, è il seguente:

• estrarre casualmente con ripetizione n osservazioni X^*₁, ..., X^*_n da X₁, ..., X_n;

• in corrispondenza di X^*₁, ..., X^*_n , calcolare med X^*₁, ..., X^*_n e (T^*=med (X^*₁, ..., X^*_n)−med (X₁, ..., X_n)

• ripetere i due passi precedenti un numero M volte; (M grande);

• la varianza di t è stimata dalla varianza campionaria di T^*, cioè

dove T_i^* è il valore di t corrispondente all’infinitesimo campione bootstrap.