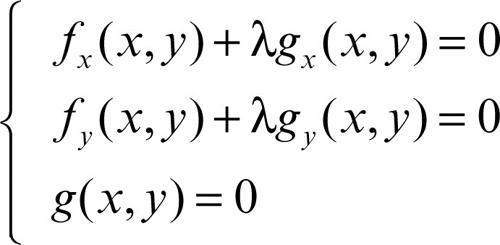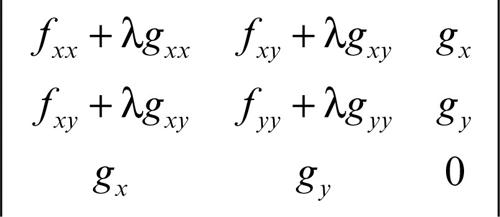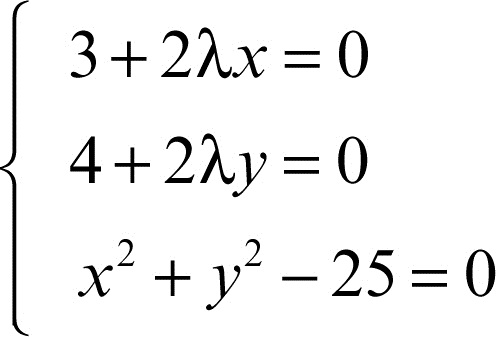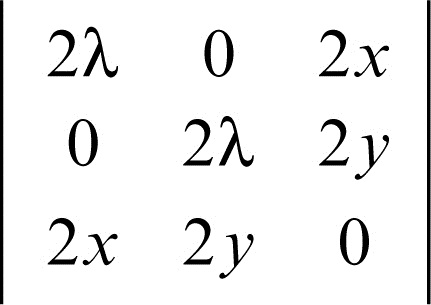Lagrange, metodo dei moltiplicatori di
Lagrange, metodo dei moltiplicatori di
Lagrange, metodo dei moltiplicatori di metodo impiegato nei problemi di estremo (massimo o minimo) vincolato (o, equivalentemente, condizionato) per caratterizzare gli estremanti di una funzione di due variabili ƒ(x, y), in presenza di un vincolo del tipo g(x, y) = 0. Infatti, nei punti di estremo relativo della funzione ƒ(x, y) soggetta al vincolo g(x, y) = 0, la funzione (detta lagrangiana) L(x, y, λ) = ƒ(x, y) + λg(x, y) ha un punto stazionario. Il parametro λ viene detto moltiplicatore di Lagrange. Si è dunque condotti al sistema
Se (x0, y0, λ0) è una soluzione di questo sistema, il punto P0(x0, y0) è poi di minimo (massimo) relativo vincolato se il determinante hessiano di L,
calcolato in (x0, y0, λ0), risulta minore di 0 (maggiore di 0). Per esempio, i punti della circonferenza g(x, y) di equazione x 2 + y 2 − 25 = 0 in cui è stazionaria la funzione ƒ(x, y) = 3x + 4y si ottengono dal sistema
che ammette le soluzioni (−3, −4, 1/2) e (3, 4, −1/2). L’hessiano
vale −52 in (−3, −4, 1/2), per cui il punto A(−3, −4) è di minimo, mentre B(3, 4) è di massimo (→ matrice hessiana).
La tecnica si generalizza a una funzione di n + m variabili, ƒ(x, y), con x ∈ Rn, y ∈ Rm, soggetta alle m condizioni g(x, y) = 0, con g: Rn+m → Rm. Introdotto un vettore λ costituito da m moltiplicatori, si costruisce la lagrangiana L(x, y, λ) e si impone che sia stazionaria rispetto a tutte le variabili, ottenendo un sistema di n + 2m equazioni in altrettante incognite (→ massimo vincolato).