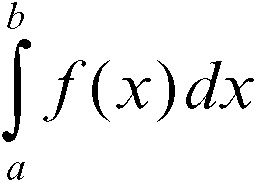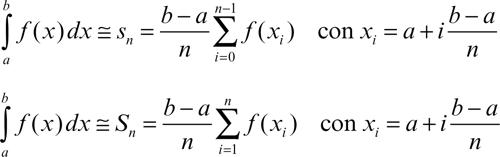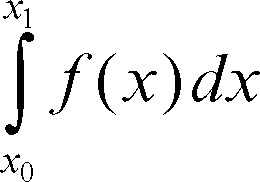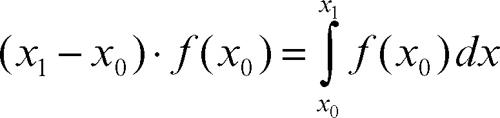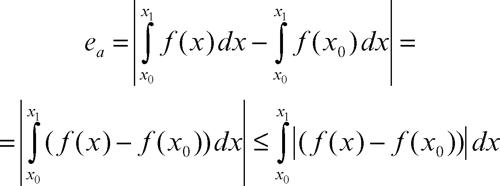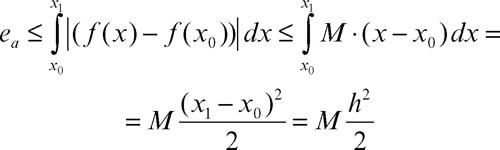rettangoli, metodo dei
rettangoli, metodo dei
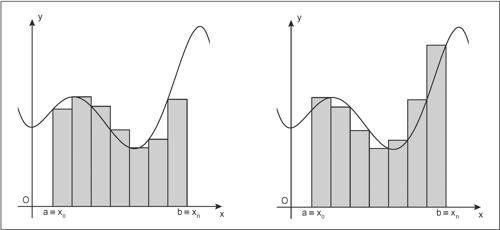
rettangoli, metodo dei metodo di integrazione numerica consistente nell’approssimare l’integrale definito
con n rettangoli aventi come base sottointervalli dell’intervallo [a, b] e come altezza il valore della funzione in corrispondenza di un punto del sottointervallo. Per una data suddivisione di [a, b] in n sottointervalli si possono considerare le due successioni {si} e {Si} aventi rispettivamente, come altezza di ogni rettangolo, la prima il valore della funzione nell’estremo sinistro del sottointervallo, la seconda il valore nell’estremo destro. Si indicano quindi con sn e Sn la somma delle aree dei rispettivi rettangoli (che nel caso per esempio di una funzione monotòna crescente in [a, b], approssimano l’integrale definito rispettivamente per difetto e per eccesso). Si scrivono così le rispettive formule di approssimazione per rettangoli:
È possibile, quindi, costruire un algoritmo che per ogni n calcoli i valori di sn e Sn finché la loro differenza non risulti inferiore a un errore δ fissato. In tale caso si sceglie come valore attendibile per l’integrale definito il valore di
diminuendo così ulteriormente l’errore commesso. Per la valutazione analitica dell’errore si può considerare uno dei sottointervalli in cui viene diviso l’intervallo d’integrazione:
Esso viene sostituito (se si considera il valore nell’estremo sinistro) con il valore approssimato:
L’errore assoluto commesso è allora:
Se la funzione integranda ƒ(x) è limitata nell’intervallo [a, b], esiste un numero reale M tale che |ƒ′ (x)| ≤ M; esiste allora (→ Lagrange, teorema di) un valore c interno all’intervallo (x0, x) per cui ƒ(x) − ƒ(x0) = ƒ′′(c)(x − x0) cioè |ƒ(x) − ƒ(x0)| = |ƒ′′(c)| |x − x0|. Qindi, |ƒ(x) − ƒ(x0)| ≤ M (x − x0), da cui
dove h indica il sottointervallo opasso d’integrazione. Ripetendo il procedimento per gli altri n sottointervalli, l’errore assoluto su tutto l’intervallo [a, b] risulta (essendo nh = b − a):