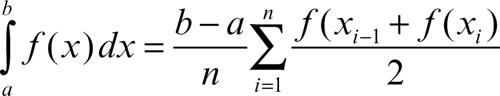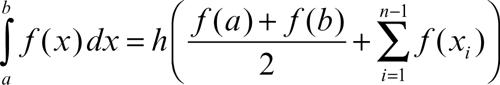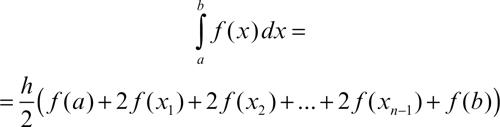trapezi, metodo dei

trapezi, metodo dei

trapezi, metodo dei metodo numerico per il calcolo approssimato dell’integrale definito di una funzione ƒ(x) nell’intervallo [a, b] (→ integrazione numerica). Per ogni suddivisione dell’intervallo con n + 1 punti equidistanti x₀ = a, x₁, x₂, …, x_n = b, si approssima la funzione ƒ nel generico sottointervallo [x_i−1, x_i] con una funzione lineare che assume gli stessi valori di ƒ in corrispondenza degli estremi x_i−1 e x_i. Il grafico della funzione risulta così costituito da una linea spezzata che lo approssima tanto meglio quanto maggiore è il numero di suddivisioni: l’integrale definito risulta approssimato dalla somma di aree di trapezi, ciascuno dei quali ha altezza (b − a)/n e basi ƒ(x_i−1) e ƒ(x_i). La sua area è, quindi:

Si ottiene la formula di approssimazione con i trapezi dell’integrale definito

con

Posto h = (b − a)/n la formula può essere riscritta come

o equivalentemente

La rapidità con cui la successione generata da questa formula converge all’integrale definito è la stessa di quella della successione ottenuta con la formula del metodo delle → tangenti: all’aumentare di n, tangente e secante tendono a coincidere. Come per il metodo dei → rettangoli, è possibile calcolare una maggiorazione dell’errore assoluto e_a: se la funzione integranda ammette derivata seconda nell’intervallo d’integrazione e se tale derivata è limitata, cioè

allora si dimostra che