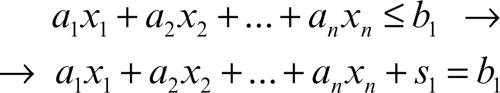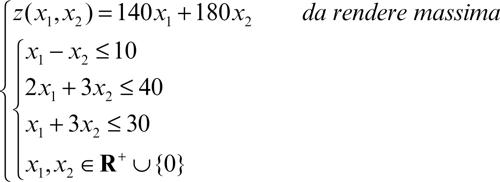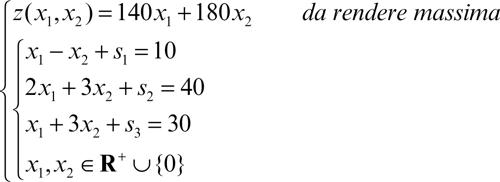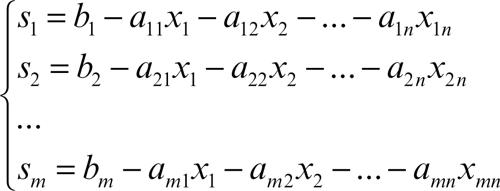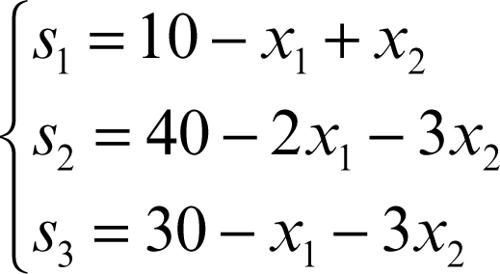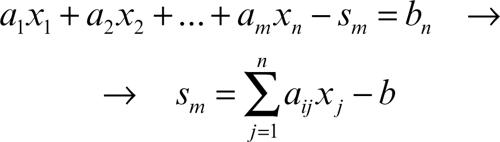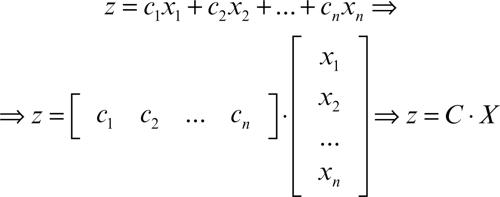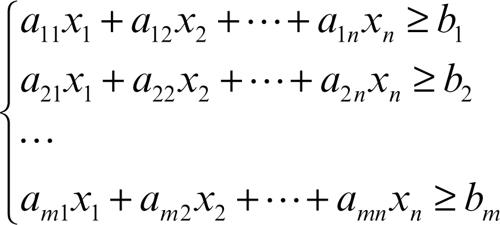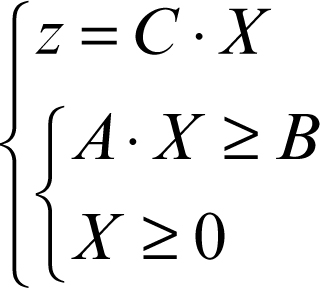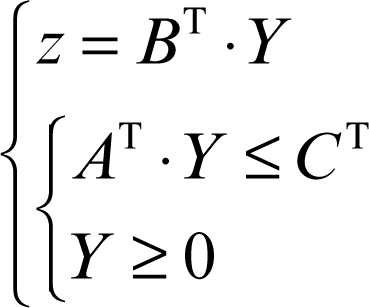simplesso, metodo del

simplesso, metodo del

simplesso, metodo del nelle applicazioni della matematica all’economia, algoritmo utilizzato per risolvere problemi di → programmazione lineare introdotto da G. Dantzig nel 1947. Consiste in una procedura iterativa, che, a partire da una determinata soluzione, consente di valutare se la soluzione ottenuta è migliorabile e, nel caso, determina una soluzione migliore della precedente. Per applicare tale metodo è necessario preliminarmente che ogni disequazione sia trasformata in equazione, introducendo le cosiddette variabili di scarto, cioè quantità che si aggiungono o si tolgono a ciascuna disequazione:

e

Il modello da analizzare è quindi costituito da un insieme di equazioni lineari, cioè da una → funzione obiettivo, lineare, e da un insieme di equazioni di primo grado a cui, trattandosi di variabili economiche, si aggiungono i vincoli di non negatività. Nel caso semplificato di una funzione obiettivo di due variabili da ottimizzare, il sistema costituito dalle disequazioni individua, nel piano cartesiano, una regione convessa del piano (che se è finita è a contorno poligonale), detta campo di scelta, all’interno del quale si trovano le possibili soluzioni del problema (dette soluzioni ammissibili); a uno dei vertici del contorno poligonale del campo di scelta, dove si trovano le cosiddette soluzioni ammissibili di base, si trova, se esiste, la soluzione ottima. Nel caso generale con n variabili, i vertici del campo di scelta sono i vertici di un → simplesso euclideo, donde il nome di tale metodo.

Problemi di massimo

Dato un modello di programmazione lineare, per esempio

introducendo le variabili di scarto s₁, s₂, s₃ esso si trasforma in

ed è possibile applicare il metodo del simplesso. Esso è costituito da due fasi, di cui la seconda costituisce la parte iterativa e fa perno sul → pivot:

1) si individua una prima soluzione ammissibile di base e si valuta la funzione obiettivo per tale soluzione, per esempio partendo dai valori minimi che possono assumere le variabili di scarto;

2) si migliora la soluzione facendo in modo di far “entrare” nella soluzione una variabile precedentemente nulla o di valore minimo, azzerando una delle variabili di scarto, che così “esce” dalla soluzione.

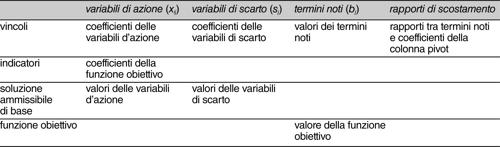
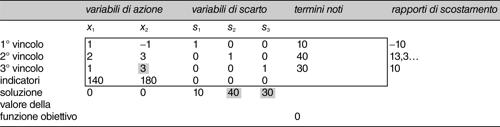
Si costruisce quindi una tavola, detta tavola del simplesso, nella quale sono racchiusi i principali valori e indicatori di riferimento. In genere, una prima soluzione ammissibile di base è individuata ponendo ciascuna delle variabili di azione uguale al minimo valore che può assumere, spesso il valore nullo. I valori delle variabili di scarto sono calcolati in base alle equazioni generali:

e quindi, seguendo l’esempio:

Si ottiene così una prima tavola del simplesso. Nel piano cartesiano la prima soluzione ammissibile di base è rappresentata dall’origine del sistema di riferimento. Per migliorare la soluzione, trattandosi di un problema di massimo, il pivot è individuato nel seguente modo:

a) si considera la colonna delle variabili d’azione con il maggior coefficiente nella riga degli indicatori (i coefficienti delle variabili della funzione obiettivo), che corrisponde alla variabile che potenzialmente può incrementare di più la funzione obiettivo: si ottiene così la colonna pivot;

b) si considera quindi la riga il cui rapporto di scostamento positivo sia minimo (essendo il rapporto di scostamento, per ogni riga, il rapporto tra il termine noto e il rispettivo coefficiente della colonna pivot): si ottiene così la riga pivot;

c) la tavola viene quindi trasformata facendo in modo di rendere il pivot uguale all’unità e nulli tutti gli altri elementi della colonna pivot.

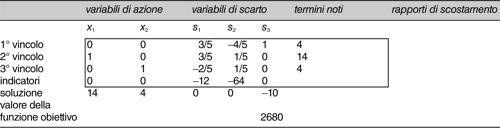
Sulla nuova tavola così costruita si itera la procedura dal punto a) al punto c) fino ad arrivare a una tavola che soddisfi il test di fine, che consiste nel fatto che nella riga degli indicatori non vi sono valori positivi.

La tavola fornisce a questo punto la soluzione ottima, che, per l’esempio in esame, è x₁ = 14 e x₂ = 4.

Problemi di minimo

In tali problemi, nei quali occorre rendere minima la funzione obiettivo, le disuguaglianze si presentano in generale nella forma

Per questo tipo di disuguaglianze si sottrae una quantità, in modo da trasformarle in uguaglianze. Così facendo però, partendo dalla prima soluzione ammissibile di base, ottenuta imponendo che siano nulle le variabili di azione, la variabile di scarto s avrebbe valore negativo:

Trattandosi di variabili economiche si preferisce evitare questo fatto e si introducono perciò ulteriori variabili, dette variabili artificiali, il cui unico scopo è quello di non rendere negativa alcuna variabile economica. Queste variabili non hanno alcun significato specifico e vengono introdotte anche nella funzione obiettivo, con coefficiente arbitrario, ma molto grande, proprio per evidenziare la loro artificiosità. Al termine del processo di calcolo della soluzione, tali variabili dovranno comparire con coefficiente nullo nella funzione obiettivo; se così non fosse il problema non ha soluzione. Anche per i problemi di minimo si può utilizzare, opportunamente modificato, il metodo del simplesso, tuttavia poiché in linea di principio è sempre possibile trasformare un problema di massimo in un problema di minimo, e viceversa, i problemi di minimo sono spesso ricondotti a problemi di massimo, in generale più facili da studiare.

Problema duale

Un problema iniziale, detto problema primale, può essere trasformato nel suo equivalente, detto problema duale. Se si indica con C il vettore riga dei coefficienti di una funzione di n variabili è con X il vettore colonna delle variabili, allora, con notazione matriciale, la funzione può essere più sinteticamente così scritta:

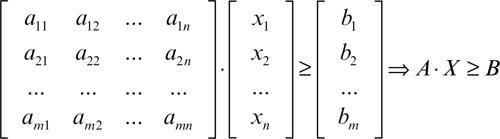
Analogamente si può riscrivere in forma matriciale un sistema di disequazioni, che per semplicità si suppongono tutte di maggioranza. Dato perciò il sistema di disequazioni

indicando con A la matrice dei coefficienti delle variabili e con B il vettore colonna dei termini noti, si ha:

Il modello matematico di un problema, può dunque essere sintetizzato con la seguente scrittura:

Se questo modello matematico rappresenta un problema che si considera primale, allora il suo problema duale è sinteticamente descritto dal seguente insieme di relazioni, dove Y rappresenta un vettore di variabili in numero uguale a quello dei vincoli del problema primale e A^T la matrice trasposta della matrice A dei coefficienti delle variabili x_i:

Per ottenere le soluzioni del problema primale da quelle del problema duale si utilizzano i seguenti risultati:

• il valore ottimo della funzione obiettivo, quando esiste, è uguale nel primale e nel duale;

• se una variabile d’azione nella soluzione ottimale del primale è diversa da 0, allora la corrispondente variabile di scarto del problema duale deve essere uguale a 0;

• se una variabile di scarto del primale è diversa da 0, allora la corrispondente variabile d’azione deve essere uguale a 0.