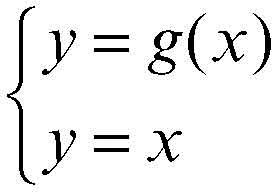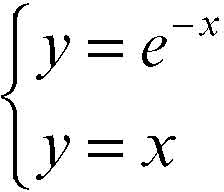attrattore, metodo dell'

attrattore, metodo dell'

attrattore, metodo dell’ (per la risoluzione di una equazione) detto anche metodo del punto unito, si basa sulla separazione dell’equazione ƒ(x) = 0 in due componenti, una formata dalla sola variabile x e l’altra dal resto dell’espressione; l’equazione viene così riscritta nella forma x = g(x). Quest’ultima è interpretabile come l’equazione risolvente il sistema:

Le soluzioni del sistema sono anche soluzioni dell’equazione data e corrispondono alle ascisse x dei punti di intersezione dei rispettivi grafici di y = x e y = g(x). Per esempio, per risolvere l’equazione e^−x − x = 0 si cercano numericamente le intersezioni tra i grafici delle due funzioni y = x e y = e^−x:

Per ricavare tale intersezione si costruisce, a partire da un valore iniziale x₀, una successione di valori

calcolando iterativamente x_i+1 = g(x_i).

La condizione di arresto dell’iterazione può essere data nella forma

decidendo di terminare il calcolo quando la differenza tra due iterazioni successive è sufficientemente piccola (cioè minore del valore ε arbitrariamente fissato).

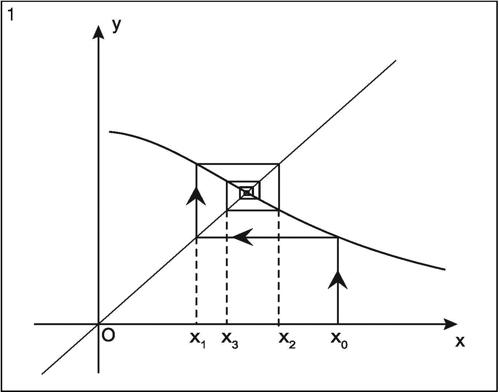
Se la successione è convergente, allora il valore x_a cui essa converge è una soluzione dell’equazione data ed è l’ascissa del punto di intersezione di y =x e y = g(x). In tal caso, il punto di intersezione dei due grafici è detto attrattore. Nell’esempio dato, prendendo come valore iniziale x₀ = 0, 2, si ottiene una successione numerica i cui punti formano sul grafico una particolare forma a spirale che individua visivamente il punto attrattore.

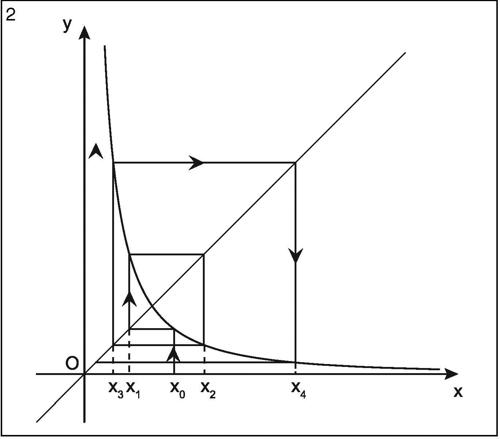
Se la successione diverge, vi sono due possibilità: a) l’intersezione non esiste, quindi l’equazione non ha soluzione; b) l’intersezione esiste e l’equazione ha soluzione, ma il metodo non permette di avvicinarsi a essa con successive iterazioni (data la disposizione reciproca dei grafici di y = x e di y = g(x)). Il punto di intersezione dei due grafici è detto per questo punto repulsore. Il significato geometrico del repulsore è reso evidente dal grafico che mostra una successione divergente di valori pur esistendo l’intersezione tra le due funzioni.

Si può dimostrare che la convergenza o la divergenza del metodo dipendono dalla posizione del punto da cui si avvia l’iterazione (il valore x₀) e dalla pendenza assoluta in esso del grafico della funzione g (che si suppone derivabile):

(cioè dal valore assoluto della derivata di g(x) calcolata in x₀). Una condizione sufficiente affinché l’algoritmo costruito con il metodo dell’attrattore converga è che

nella regione interessata all’intersezione. In questo caso la pendenza assoluta del grafico di g(x) è minore di quella della bisettrice e le iterazioni portano il punto «sempre più vicino» all’attrattore. Se l’algoritmo non converge, perché la pendenza assoluta della funzione y = g(x) è maggiore di 1, si può operare una simmetria del grafico della funzione rispetto alla bisettrice y = x. Con questa trasformazione, il punto di intersezione con la bisettrice non cambia ma la pendenza assoluta della curva trasformata è minore di 1.