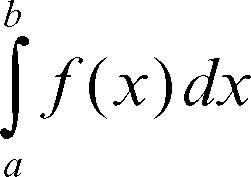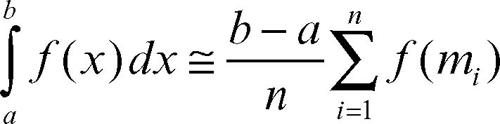tangenti, metodo delle

tangenti, metodo delle

tangenti, metodo delle (per il calcolo di un integrale definito) metodo numerico per il calcolo approssimato dell’integrale definito

la cui formula di approssimazione è

dove a e b rappresentano gli estremi dell’intervallo di integrazione [a, b] e n è il passo di integrazione in cui si suddivide l’intervallo [a, b] per ottenere n sottointervalli di uguale lunghezza

Il numero

è il punto medio di ciascun sottointervallo [x_i−1, x_i] e ƒ(m_i) è il valore della funzione in corrispondenza del punto medio m_i. Il rettangolo ABCD che ha per base il sottointervallo di estremi x_i−1 e x_i e per altezza ƒ(m_i) è equivalente al trapezio ABC′D′, il cui lato C′D′ è tangente (da cui il nome del metodo) al grafico della funzione nel punto P(m_i, ƒ(m_i)).

La regione del piano di cui si desidera calcolare l’area è quella compresa tra il grafico della funzione ƒ(x) nell’intervallo [a, b] e l’asse delle ascisse; essa viene quindi approssimata da n trapezi aventi tutti il lato obliquo tangente al grafico della funzione. All’aumentare del passo d’integrazione n l’approssimazione migliora fortemente. Si dimostra che la formula delle tangenti tende più rapidamente al valore dell’integrale definito rispetto a quella generata dalle successioni ottenute con il metodo dei rettangoli. Nella costruzione dell’algoritmo di calcolo si stabilisce di interrompere la procedura quando il valore assoluto della differenza tra due approssimazioni successive risulta minore di una quantità piccola prefissata (→ integrazione numerica; → rettangoli, metodo dei).