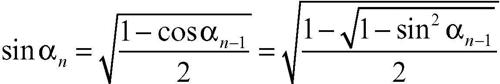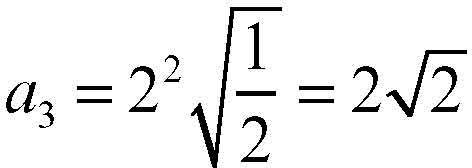Archimede, metodo di

Archimede, metodo di

Archimede, metodo di (per pi greco) procedura geometrica formulata da Archimede per il calcolo approssimato di π (da cui anche il nome di numero di Archimede, attribuito a volte a π). Nel metodo di Archimede si considera innanzitutto π come il numero che esprime l’area del cerchio di raggio unitario e, conseguentemente, si costruisce la successione delle aree dei poligoni regolari inscritti in tale cerchio e aventi un numero sempre maggiore di lati. Indicata con a_n l’area del poligono regolare inscritto nel cerchio di raggio unitario e avente 2ⁿ lati, per n = 2, 3, 4, ..., si ha che:

• per n = 2 il poligono ha 2² lati ed è il quadrato avente le diagonali di lunghezza 2,

• per n = 3 si ottiene un ottagono regolare,

• per n = 4 si ha un poligono regolare di 16 lati, e così via.

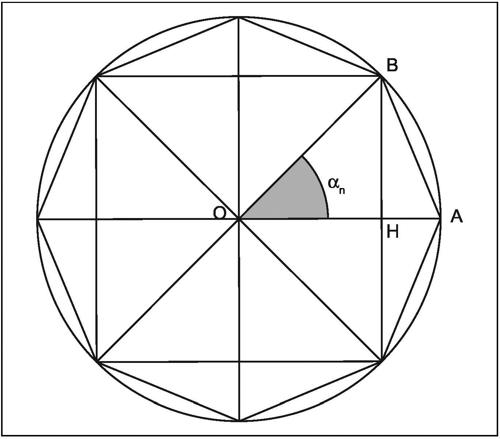
Si consideri il caso n = 3; sia AB il lato dell’ottagono regolare di centro O, sia H il piede della perpendicolare a OA tracciata da B; si generalizzi quindi il ragionamento per un intero n ≥ 2 qualsiasi.

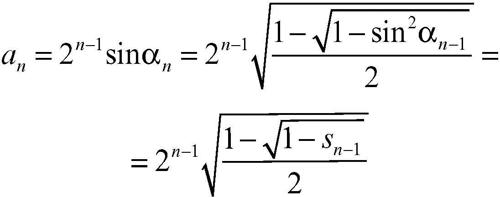
Poiché OA = OB = 1, BH = sinα_n, con α_n = 360°/2ⁿ, l’area a_n del poligono regolare di 2ⁿ lati risulta:

Si ottiene una successione {a_n} di valori numerici che approssimano l’area del cerchio. È una successione convergente e π è il valore a cui converge (per n tendente all’infinito). Si noti che per ogni poligono l’ampiezza dell’angolo α_n è metà di quella del poligono precedente:

Per la formula di bisezione per il seno:

da cui

dove si è indicato per semplicità s_n = sinα_n. Si ha così una regola ricorsiva per la costruzione della successione {a_n}. Nei casi particolari del quadrato e dell’ottagono, si ha:

• per n = 2, a₂ = 2¹ · 1 = 2 (area del quadrato, essendo α₂ = 90° e s₂ = sin(90°) = 1);

• per n = 3, s₃ si ricava da s₂ con la formula di bisezione, ed è pari a 1/2, quindi:

(area dell’ottagono inscritto).

Un algoritmo di calcolo per valori approssimati di π può quindi essere costruito introducendo un indice i, tale che 2ⁱ è il numero dei lati del poligono considerato, e una variabile l che indica il numero dei lati del poligono che lo precede nella successione di figure; s è una variabile che indica il seno dell’angolo α. Si ha, quindi:

Al crescere di n, la successione delle aree {a_n} che così si costruisce tende a π. I valori ottenuti sono approssimazioni per difetto di π; si può costruire una successione {A_n} di sue approssimazioni per eccesso considerando una successione di poligoni regolari circoscritti al cerchio, aventi 2ⁿ lati (con n ≥ 2). A partire dalle due successioni {a} e {A_n}, si può ottenere una migliore approssimazione di π considerando la successione delle medie geometriche dei corrispondenti valori (per difetto e per eccesso) delle due successioni.