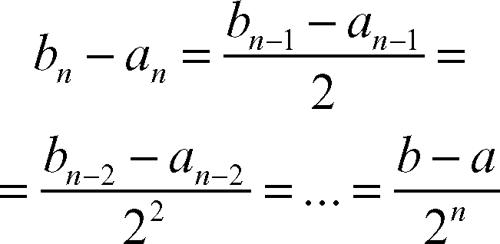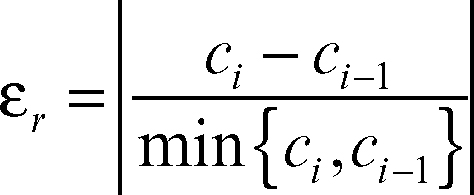bisezione, metodo di

bisezione, metodo di

bisezione, metodo di (per la risoluzione di una equazione) procedimento numerico iterativo per la determinazione di una soluzione di un’equazione ƒ(x) = 0, all’interno di un intervallo chiuso [a, b] dove la funzione ƒ è continua e nei cui estremi assume valori di segno opposto. Poiché una soluzione dell’equazione è uno zero per la funzione, l’esistenza di almeno uno zero in tale intervallo è garantita dal teorema di esistenza degli zeri (→ zeri di una funzione, teorema di esistenza degli); a meno che la funzione non sia monotòna, il metodo non garantisce che la soluzione trovata sia l’unica nell’intervallo considerato.

Il procedimento consiste nel dividere l’intervallo assegnato in due sottointervalli mediante il punto medio c e, se la funzione ƒ non si annulla in c (nel qual caso c è una soluzione), nel considerare quello dei due sottointervalli nei cui estremi ƒ assume valori di segno opposto; in tale sottointervallo si ripete il procedimento. Procedendo in questo modo o si perviene, dopo un numero finito di iterazioni, a un punto in cui ƒ è nulla oppure si genera una successione di intervalli [a_n, b_n], ciascuno ottenuto dimezzando il precedente, i cui estremi convergono a una soluzione dell’equazione.

Se per esempio, ƒ(a) < 0 e ƒ(b) > 0 allora, ponendo a = a₀ e b = b₀ si determinano il punto medio dell’intervallo

e il valore ƒ(c₀) che la funzione assume in quel punto. Si ha che:

• se ƒ(c₀) ha segno diverso da ƒ(a₀), cioè se ƒ(a₀) · ƒ(c₀) < 0, uno zero della funzione si trova nel sottointervallo di sinistra [a₀, c₀], per cui si può procedere con l’iterazione ponendo a₁ = a₀ e b₁ = c₀ e calcolando il punto medio

• se ƒ(a₀) · ƒ(c₀) > 0, uno zero si trova nel sottointervallo di destra [c₀, b₀], per cui si sceglie a₁ = c₀ e b₁ = b₀;

• se ƒ(a₀) · ƒ(c₀) = 0 allora c₀ è uno zero.

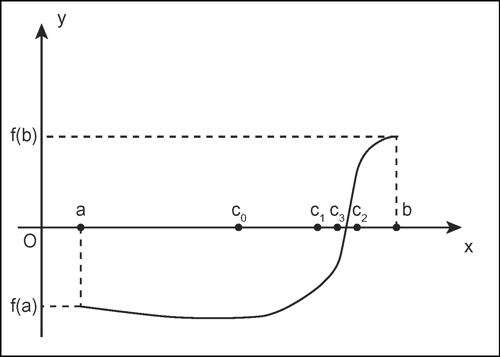
Il metodo procede scegliendo il sottointervallo opportuno nei cui estremi la funzione assume segni opposti. Nell’esempio in figura, alla prima e seconda iterazione si sceglie l’intervallo a destra, mentre dopo la seconda, si considera l’intervallo di sinistra, poiché la funzione assume agli estremi c₂ e b valori entrambi positivi; si calcola così c₃. Se non risulta per qualche i, ƒ(c_i) = 0, si viene a costruire una successione di sottointervalli, ciascuno contenuto nel precedente e di ampiezza pari alla sua metà

Poiché la soluzione è sicuramente contenuta all’interno dell’intervallo, l’errore assoluto che si commette con questo metodo è

Tale errore è massimo quando la soluzione esatta si trova in prossimità di uno degli estremi, mentre è minimo quando la soluzione è prossima al centro dell’intervallo stesso. Per una stima dell’errore relativo del metodo di bisezione, poiché non si conosce il valore esatto della soluzione cercata, se ne considera una stima attraverso la quantità

Nel metodo di bisezione è sempre possibile controllare il limite superiore dell’errore: tale caratteristica, unita alla convergenza della successione delle approssimazioni, rende questo metodo uno dei più affidabili.