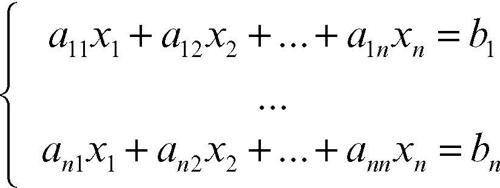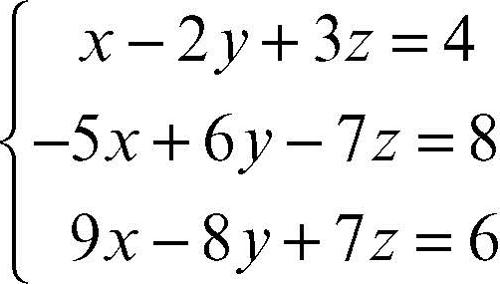Cramer, metodo di

Cramer, metodo di

Cramer, metodo di o regola di Cramer, in algebra lineare, metodo per risolvere un sistema di n equazioni lineari in n incognite quale

scritto in forma compatta come Ax = b, avente matrice dei coefficienti A = {a_ij} invertibile, cioè con determinante diverso da zero (cioè rango della matrice uguale al numero di incognite). Più in particolare, se d indica il determinante della matrice dei coefficienti A e d_i indica il determinante della matrice ottenuta da A sostituendo il vettore dei termini noti b alla sua i-esima colonna, allora il sistema ammette una e una sola soluzione data dal vettore la cui i-esima componente è d_i/d. In altri termini, il valore di ciascuna incognita si ottiene da una frazione che ha d come denominatore e al numeratore il determinante che si ottiene sostituendo in d la colonna dei termini noti alla colonna dei coefficienti dell’incognita considerata. Per esempio, nel sistema

la soluzione per la incognita x è data, una volta calcolati i determinanti delle matrici, da:

Il metodo prende il nome dal matematico svizzero G. Cramer.