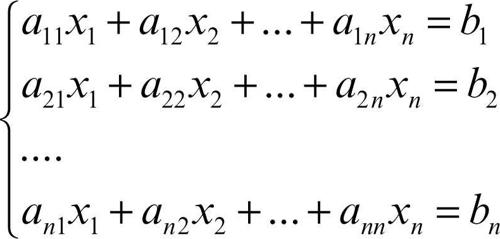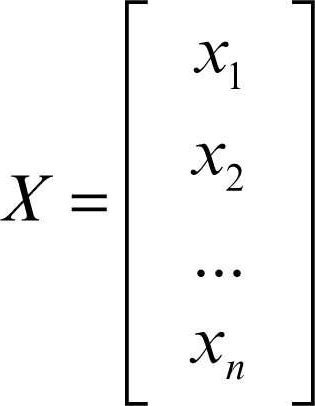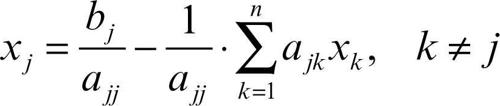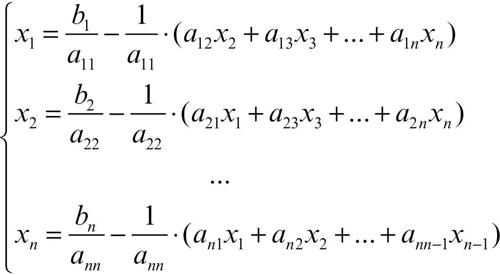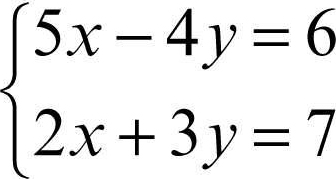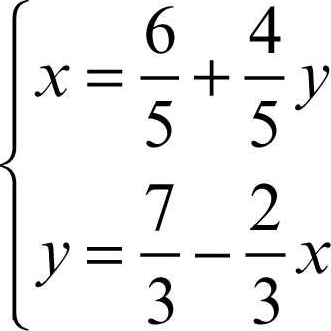Gauss-Seidel, metodo di

Gauss-Seidel, metodo di

Gauss-Seidel, metodo di procedimento iterativo per la ricerca delle soluzioni di un sistema di equazioni lineari attraverso → approssimazioni successive (si veda anche la voce → approssimazione (di una soluzione)). È detto anche metodo delle sostituzioni successive e risulta utile quando il numero delle incognite è molto grande. Si consideri il caso di un sistema di equazioni lineari in cui il numero n di equazioni sia uguale al numero n delle incognite:

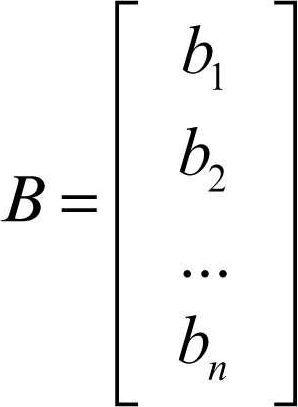
In forma matriciale il sistema si può scrivere nella forma più compatta, AX = B, dove

è la matrice quadrata dei coefficienti,

è il vettore delle soluzioni e

è il vettore dei termini noti. Esplicitando le incognite in ogni equazione del sistema si ottiene:

È possibile, quindi, riscrivere il sistema nella forma seguente:

Data una n-pla ordinata di soluzioni approssimate

applicando il metodo iterativo scelto, si ottiene una nuova n-pla X⁽¹⁾; continuando il procedimento si ottiene via via una successione di soluzioni approssimate

Se esiste finito il

allora la successione converge e tale limite è la soluzione del sistema. Il valore iniziale della prima n-pla non è rilevante. Infatti, essa può essere approssimata anche grossolanamente, per esempio scegliendo l’n-pla nulla, perché si dimostra che se la successione è convergente lo è per una qualsiasi scelta arbitraria dei valori iniziali: la n-pla, per così dire, si autocorregge a ogni passo del metodo. Il metodo di Gauss-Seidel consiste proprio nel sostituire, come primo passo, nella prima equazione i valori iniziali delle variabili (x₁, x₂, ..., x_n), con una (n − 1)-pla arbitraria, per esempio quella avente tutti gli elementi nulli, e ricavare quindi il valore approssimato x₁⁽¹⁾:

Tale valore si sostituisce nella seconda equazione per determinare il valore di x₂⁽¹⁾:

Per calcolare x₃⁽¹⁾ si usano i valori già determinati di x₁⁽¹⁾ e x₂⁽¹⁾ e così via. Una volta sostituiti i valori nell’ultima equazione, si ottiene la prima n-pla approssimata

Diversamente dal metodo di → Jacobi, che prevede una sostituzione simultanea delle variabili, nel metodo di Gauss-Seidel si calcola il risultato per ciascuna equazione, utilizzando i risultati ottenuti dalle equazioni precedenti. I criteri per porre termine all’iterazione e i criteri di convergenza della soluzione dipendono dalle seguenti condizioni della matrice A dei coefficienti:

• condizione necessaria per la convergenza è che tutti gli elementi della diagonale principale di A siano diversi da zero: (a₁₁, a₂₂, …, a_nn) ≠ (0, 0, ..., 0);

• condizione sufficiente è che A sia una matrice a predominanza diagonale, cioè che ciascun elemento appartenente alla diagonale principale sia maggiore in valore assoluto della somma degli elementi della riga corrispondente: |a_kk| > |a_k1| + |a_k2| + ... + |a_kn| con k = 1, 2, ..., n.

Il metodo di Gauss-Seidel possiede un’interessante interpretazione geometrica: sia dato per esempio il seguente sistema a due equazioni e due variabili:

Le equazioni sono rappresentate nel piano cartesiano da due rette; risolvere il sistema equivale a trovare le coordinate del loro punto di intersezione. Esplicitando le due variabili in ciascuna equazione si trova:

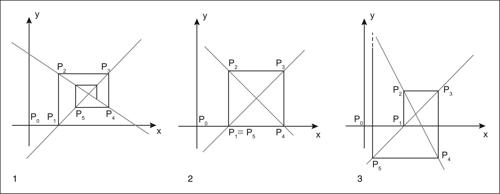
Considerando come punto iniziale il punto P₀(0, 0), si sostituisce a y il valore 0 nella prima equazione e si calcola x ottenendo

Il punto

è la prima approssimazione del risultato. Sostituendo il valore 6/5 alla x della seconda equazione si ha

da cui con la sostituzione nella prima equazione si ottiene

valore da sostituire nella seconda per ottenere P₄ e così via: da ogni punto trovato si traccia alternativamente una parallela all’asse x o all’asse y fino a incontrare l’altra retta. Il punto d’intersezione è il nuovo punto da cui si inizia una nuova iterazione. L’esempio precedente è un caso di sistema convergente. Come si può dedurre dal grafico, la convergenza o meno del sistema dipende fortemente dalla pendenza reciproca delle due rette. Si possono avere casi in cui il sistema non converge: in alcuni casi si ha un sistema oscillante, in cui la soluzione calcolata rimane in una zona prossima alla soluzione, rappresentata dall’intersezione delle due rette, perché, ripetendo gli stessi valori, non le si avvicina mai. In un sistema divergente, infine, la soluzione si allontana indefinitamente dal punto di intersezione delle rette all’aumentare del numero di iterazioni.

Il metodo di Gauss-Seidel è in genere più veloce del metodo di Jacobi perché usa immediatamente i valori calcolati nell’iterazione corrente.