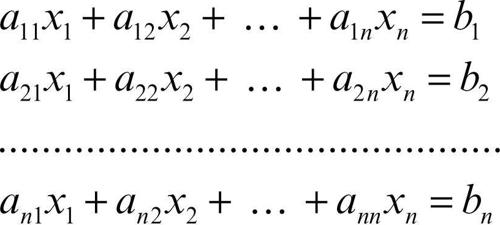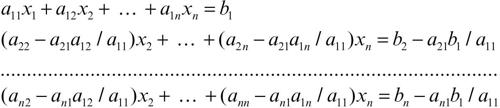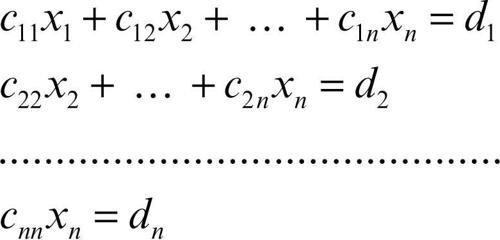Gauss, metodo di

Gauss, metodo di

Gauss, metodo di o eliminazione di Gauss, in algebra lineare, algoritmo per la risoluzione numerica di un sistema di n equazioni lineari in n incognite della forma

fondato su una sequenza di passi basati sulle due seguenti operazioni elementari, che trasformano un sistema di equazioni in un sistema equivalente: 1) se a una equazione del sistema si sostituisce l’equazione ottenuta da essa moltiplicandola per una costante, allora si ottiene un sistema equivalente; 2) se a una equazione del sistema si sostituisce l’equazione ottenuta da essa sommandola a un’altra equazione del sistema, allora si ottiene un sistema equivalente.

Più precisamente, il metodo di Gauss si articola nei seguenti n − 1 passi, ognuno dei quali ripete quanto fatto al passo precedente su un sistema di dimensione minore:

• passo 1: si ricava dalla prima equazione l’incognita x₁ in funzione delle incognite successive x₂, x₃, ..., x_n nella forma

e la si sostituisce nelle altre equazioni, da cui essa viene in questo modo eliminata. Ci si riconduce in questo modo a un sistema equivalente, della forma

• passo 2: si applica quanto fatto al passo precedente al sistema, di n − 1 equazioni in n − 1 incognite, espresso dalle ultime n − 1 equazioni del sistema determinato al passo precedente, da cui è stata eliminata l’incognita x₁. Ci si riconduce in questo modo a un sistema di n equazioni in n incognite in cui la prima equazione è la prima equazione del sistema iniziale, la seconda equazione è la seconda equazione del sistema determinato al passo 1 e le restanti equazioni dipendono solamente dalle incognite x₃, x₄, ..., x_n.

• passo n − 1: si applica quanto fatto al passo precedente al sistema, di 2 equazioni in 2 incognite, espresso dalle ultime 2 equazioni del sistema determinato al passo precedente, che dipendono solamente dalle incognite x_n−1, x_n. Ci si riconduce in questo modo a un sistema di n equazioni in n incognite in cui la prima equazione è la prima equazione del sistema iniziale, la seconda equazione è la seconda equazione del sistema determinato al passo 1, ..., la (n − 1)-esima equazione è la (n − 1)-esima equazione del sistema al passo n − 2 e la restante equazione dipende solamente dall’incognita x_n. Tale sistema è un sistema a scala, vale a dire la matrice dei coefficienti è triangolare superiore: un tale sistema ha la forma caratteristica

per opportuni valori c_ij e d_i determinati dall’algoritmo ed è risolubile a cascata: dall’ultima equazione si ricava il valore dell’incognita x_n; tale valore viene dunque inserito nella penultima equazione e si ricava così il valore dell’incognita x_n−1, e così via fino alla completa risoluzione del sistema.

Per l’applicazione del metodo è necessario che i termini diagonali che via via si incontrano siano tutti diversi da zero: se la matrice dei coefficienti del sistema A = (a_ij) è non singolare (vale a dire se det(A) ≠ 0), allora ci si può sempre ricondurre a una situazione di questo tipo e il metodo di Gauss determina l’unica soluzione del sistema. Se, in caso contrario, la matrice dei coefficienti A è singolare, allora il sistema o ha infinite soluzioni oppure è impossibile. Il metodo di Gauss richiede l’esecuzione di un numero di operazioni aritmetiche dell’ordine di (2/3)n³.