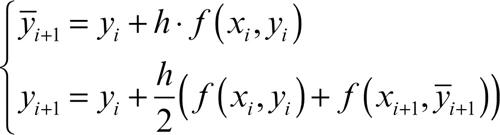Heun, metodo di

Heun, metodo di

Heun, metodo di metodo numerico per la ricerca della soluzione approssimata di una equazione differenziale ordinaria del tipo y′ = ƒ(x, y(x)), con valore iniziale y₀ = y(x₀), dove la funzione y = y(x) è definita in un intervallo chiuso e limitato [a, b] ⊂ R (si veda anche la voce → approssimazione (di una soluzione)). Tale metodo può essere considerato come una variante del metodo di → Runge-Kutta. La procedura del calcolo della soluzione avviene in due fasi distinte:

• si effettua il calcolo di un valore intermedio ȳ_i+1 corrispondente al valore approssimato che si avrebbe usando il metodo di → Eulero;

• si calcola l’approssimazione finale y_i+1 con una formula analoga a quella usata nel metodo di integrazione numerica dei trapezi (→ trapezi, metodo dei). Pertanto, il metodo di Heun permette il calcolo dei valori ȳ_i+1 e y_i+1 tramite il seguente sistema di formule:

essendo h il passo d’integrazione h = x_i+1 − x_i. Il primo passo del metodo sfrutta la condizione iniziale y₀ = y(x₀), per cui la prima equazione, per i = 0, si scrive

e la seconda

Al secondo passo nella (1) si sostituiscono alla coppia (x₀, y₀) i valori (x₁, y₁) con x₁ = x₀ + h e y₁ il valore calcolato precedentemente, ottenendo in primo luogo ȳ₂; quindi, sostituendo quest’ultimo nella (2), si ottiene il valore approssimato y₂. Iterando il procedimento nell’intervallo [a, b] con incrementi uguali al passo d’integrazione, si ottiene la successione dei valori y₀, y₁, …, y_n, che costituisce l’approssimazione per punti della funzione y = y(x) nell’intervallo [a, b], soluzione “vera” dell’equazione differenziale y′ = ƒ(x, y(x)), con valore iniziale y₀ = y(x₀).

Il metodo di Heun fa parte della classe più generale dei metodi di analisi numerica nota con il nome di metodo predittore-correttore. I metodi di questa classe consistono in una procedura che contiene due algoritmi: 1) il primo contiene l’equazione del predittore, che calcola una prima approssimazione, anche grossolana, della grandezza incognita (qualunque essa sia); 2) il secondo, attraverso l’equazione del correttore, fornisce un valore approssimato più preciso, affinando il valore approssimato che si è ottenuto con il predittore. La (1) rappresenta l’equazione del predittore che fornisce attraverso il metodo di Eulero la prima approssimazione ȳ_i+1 della soluzione, mentre la (2) rappresenta il correttore che, con il metodo dei trapezi, genera l’approssimazione finale y_i+1 (→ equazione differenziale, metodo numerico per la risoluzione di una).