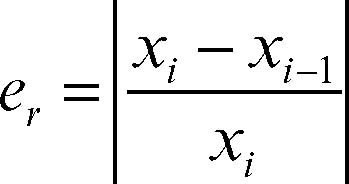Newton, metodo di

Newton, metodo di

Newton, metodo di (delle tangenti per la risoluzione di equazioni) metodo numerico per la ricerca degli zeri di una funzione y = ƒ(x) attraverso l’uso di funzioni lineari. Il metodo è utilizzato per la ricerca di una radice dell’equazione ƒ(x) = 0 quando non sia possibile individuarla utilizzando opportune formule (si veda anche → approssimazione (di una soluzione)).

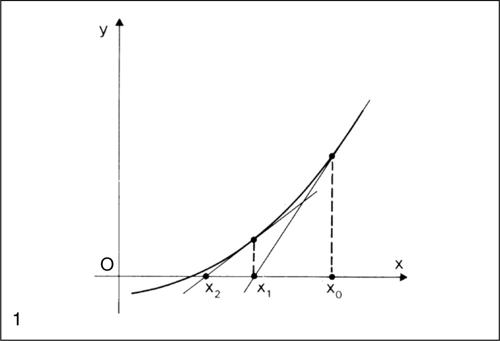
Per comprendere il metodo si individui un intervallo [a, b] in cui y = ƒ(x) sia continua e assuma valori di segno opposto agli estremi (cioè ƒ(a) ⋅ ƒ(b) < 0) e si supponga che la derivata seconda ƒ″ (x) abbia segno costante in tutti i punti interni all’intervallo: tali condizioni sono sufficienti a dimostrare che lo zero di ƒ(x) nell’intervallo considerato esiste ed è unico. Poiché ƒ(x) assume valori di segno opposto agli estremi dell’intervallo, in uno di questi estremi avrà lo stesso segno di ƒ″ (x): si assuma questo estremo come punto iniziale x₀ di un metodo iterativo. Si supponga per esempio che sia ƒ″ (x) > 0 e ƒ(b) > 0; il punto iniziale sarà quindi l’estremo b. L’equazione della tangente alla curva nel punto di ascissa x₀ è y − ƒ(x₀) = ƒ′(x₀)(x − x₀). Il punto di intersezione di tale retta con l’asse x, indicato con x₁, si ottiene ponendo y = 0 nell’equazione precedente:

Iterando il procedimento, si calcola quindi la tangente in (x₁, ƒ(x₁)) ricavando x₂ e così via. Si ottiene alla fine una successione di valori {x₀, x₁, x₂, ..., x_n} convergente al valore dello zero della funzione.

Il metodo di Newton si applica in tutti i casi in cui la funzione assume valori di segno opposto agli estremi dell’intervallo e la derivata seconda ha segno costante in esso. Per esempio, se ƒ″ (x) < 0 (la curva volge la concavità verso le ordinate negative) e ƒ(a) < 0, si ottiene ugualmente una sequenza di rette tangenti che permette di avvicinarsi progressivamente allo zero della funzione. La condizione di arresto può essere scritta nella forma |x_i − x_i−1| < ε, stabilendo di terminare il procedimento quando la differenza tra due approssimazioni successive è sufficientemente piccola; alternativamente, la medesima condizione può essere data sotto la forma |ƒ(x_i)| < ε, in cui il valore che la funzione assume nel punto x_i è in valore assoluto sufficientemente vicino allo zero. Più che l’errore assoluto in questo metodo è interessante considerare l’errore relativo. Infatti, non disponendo del valore esatto della soluzione, si ricorre alla stima dell’errore tramite il rapporto:

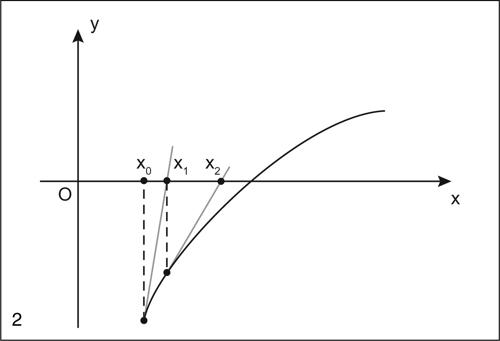
È la stessa modalità attuata anche nel metodo delle secanti, sempre per la ricerca di una radice di un’equazione; in entrambi i metodi l’errore decresce piuttosto rapidamente. In particolare, nel metodo di Newton l’errore è all’incirca proporzionale al quadrato dell’errore del passo precedente: ciò significa che il numero di cifre decimali esatte raddoppia a ogni iterazione. Questa caratteristica è detta convergenza quadratica dell’algoritmo. Se nell’intervallo [a, b] esiste una sola soluzione, individuabile graficamente e la cui esistenza è assicurata dalla costanza del segno di ƒ′ (x), ma la derivata seconda non ha segno costante, il metodo di Newton può non convergere e la soluzione approssimata oscilla intorno a un punto di massimo relativo della funzione.