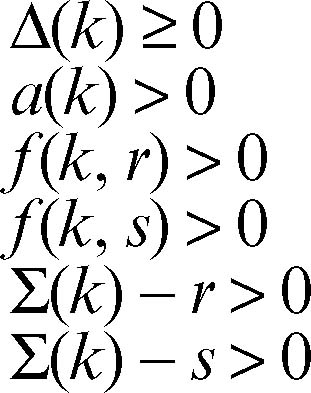Tartinville, metodo di

Tartinville, metodo di

Tartinville, metodo di in algebra elementare, metodo per la discussione di un sistema misto in una incognita, costituito da una equazione di secondo grado ƒ(x) = 0, i cui coefficienti dipendono da un parametro reale k, e da una o due disequazioni lineari, del tipo x ≤ s oppure x ≥ r oppure r ≤ x ≤ s. Il metodo prende il nome dal matematico francese A. Tartinville. Data una equazione di secondo grado in un’incognita con parametro della forma a(k)x ² + b(k)x + c(k) = 0, dove i coefficienti dell’incognita x sono funzioni di un parametro k, e assegnati due valori r e s (detti valori limite), il metodo permette di stabilire per quali valori del parametro k esistano (e in quale numero) soluzioni dell’equazione comprese fra i due valori limite. Il procedimento consiste nel risolvere una serie di disequazioni, in cui l’incognita è il parametro k, che saranno poi opportunamente studiate. Sia

la funzione, nelle due variabili k e x, di cui si ricercano gli zeri e siano

e

rispettivamente il discriminante e la semisomma delle radici dell’equazione di secondo grado da studiare in x. Si risolvano le seguenti disequazioni nell’incognita k:

Impostando il sistema formato da tali disequazioni e studiando caso per caso l’esistenza e l’unicità delle soluzioni nei singoli intervalli, si distinguono vari casi:

• negli intervalli in cui Δ(k) < 0, non esistono soluzioni reali dell’equazione;

• negli intervalli in cui Δ(k) = 0, esiste una sola soluzione reale:

a) nei sottointervalli in cui Σ(k) − r e Σ(k) − s hanno segno concorde, la soluzione non è compresa tra i valori limite assegnati;

b) nei sottointervalli in cui Σ(k) − r e Σ(k) − s hanno segno discorde, la soluzione è compresa tra i valori limite assegnati;

• negli intervalli in cui Δ(k) > 0, esistono due soluzioni reali distinte:

a) nei sottointervalli in cui ƒ(k, r) e ƒ(k, s) hanno segno discorde, solamente una soluzione è compresa tra i valori limite assegnati;

b) nei sottointervalli in cui ƒ(k, r) e ƒ(k, s) hanno segno concorde, ma discorde dal segno di a(k), nessuna soluzione è compresa tra i valori limite assegnati;

c) nei sottointervalli in cui ƒ(k, r), ƒ(k, s) e a(k) hanno segno concorde tra di loro e Σ(k) − r e Σ(k) − s hanno segno concorde tra di loro, nessuna soluzione è compresa tra i valori limite assegnati;

d) nei sottointervalli in cui ƒ(k, r), ƒ(k, s) e a(k) hanno segno concorde tra di loro e Σ(k) − r e Σ(k) − s hanno segno discorde tra di loro, entrambe le soluzioni sono comprese tra i valori limite assegnati.