Montecarlo, metodo
Montecarlo, metodo
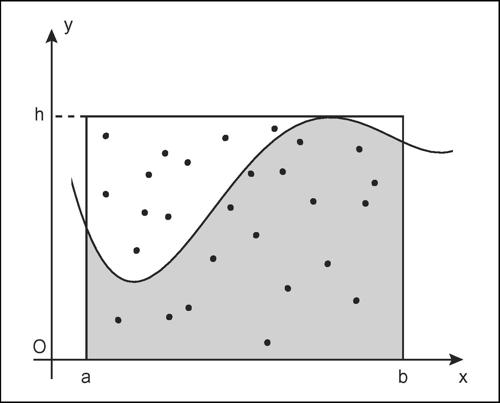
Montecarlo, metodo locuzione con cui si indica un metodo di simulazione che applica un modello probabilistico, cioè un modello la cui evoluzione è regolata dall’esito di eventi casuali, a problemi sostanzialmente deterministici e in particolare a problemi fisici o di calcolo numerico. Esso fa riferimento alla legge dei grandi numeri, secondo la quale si presume che, dopo un gran numero di prove, la frequenza di successi sia assimilabile alla probabilità teorica. Per utilizzare il metodo Montecarlo con efficacia è necessario, quindi, effettuare un gran numero di prove; infatti, tale metodo ha cominciato a svilupparsi proprio in coincidenza con lo sviluppo dei primi elaboratori elettronici, in considerazione delle ampie potenzialità di calcolo che questi offrivano. Una delle numerose applicazioni del metodo è la valutazione di aree di figure piane non altrimenti calcolabili con facilità. Può per esempio essere utilizzato per calcolare l’area della superficie sottostante al grafico di una funzione y =ƒ(x), definita e positiva nell’intervallo [a, b], vale a dire della superficie delimitata dal grafico della funzione, dall’asse x e dalle rette x = a e x = b, quando non sia elementarmente individuabile la primitiva della funzione. Si inscrive tale superficie in un rettangolo che la contenga tutta e che sia individuato sull’asse delle ascisse dall’intervallo [a, b] e sull’asse delle ordinate dall’intervallo [0, h], dove h è il massimo della funzione. Il metodo consiste nel generare, di volta in volta, un punto casuale, cioè due numeri casuali compresi rispettivamente nell’intervallo [a, b] per l’ascissa e nell’intervallo [0, h] per l’ordinata, e nel calcolare il rapporto tra i punti che cadono all’interno della superfide e tutti i punti generati; tale rapporto, confrontato con l’area del rettangolo, tenderà a fornire una buona approssimazione dell’area della superficie cercata. Non è tuttavia sempre semplice stabilire univocamente la modalità della procedura di generazione casuale; sulle possibili difficoltà, si veda il paradosso noto come ago di → Buffon.