minimax
minimax
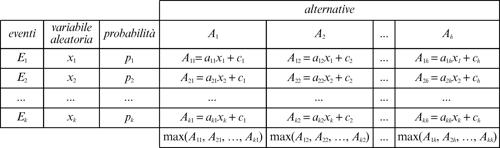
minimax criterio utilizzato nelle applicazioni della matematica all’economia e in teoria dei → giochi per limitare al massimo le eventuali perdite in situazioni di incertezza. Esso consiste nel seguente principio: in problemi di scelta tra più alternative, nel caso di possibili perdite, si sceglie l’alternativa che presenta il minimo valore tra quelli massimi di perdita. Per esempio, per una generica funzione del costo k(x) = ax + c, si ha la matrice generale dei risultati di seguito indicata e i valori tra i quali effettuare la scelta.
Facendo riferimento alla matrice dei risultati economici (→ ottimizzazione), per ogni alternativa si individua il massimo tra i valori della rispettiva colonna e, tra questi massimi, si individua il minimo. Il criterio è spesso utilizzato nella teoria dei giochi a somma zero, cioè nel caso in cui guadagni o perdite di un giocatore (operatore economico) sono speculari a perdite o guadagni di un secondo giocatore (secondo operatore economico). Se A e B sono due operatori economici (due giocatori) e ciascuno può effettuare tre diverse scelte, un esempio di matrice dei risultati con gioco a somma zero è la seguente:
In questa matrice il valore +3 nella prima cella dei risultati economici significa che se A sceglie la strategia A1 e B sceglie la strategia B1, allora B cede +3 ad A. In base al criterio del minimax, l’operatore A sceglierà la strategia A2, poiché il valore negativo −1 corrisponde alla minore perdita tra quelle possibili. Il criterio del minimax è sostanzialmente speculare a quello del → maximin.