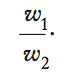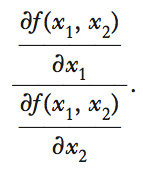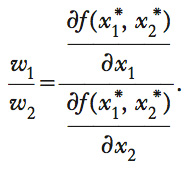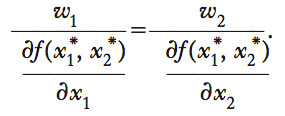costi, minimizzazione dei
costi, minimizzazione dei
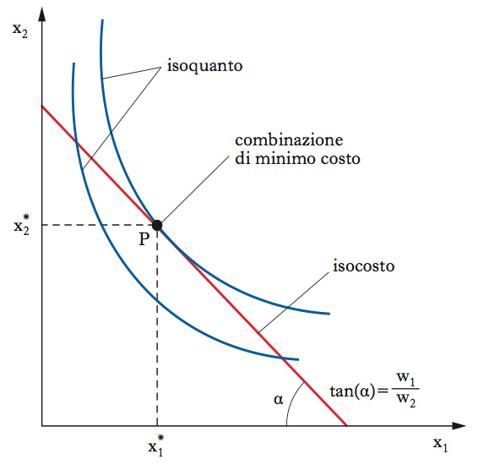
Nella teoria economica, condizione che si realizza quando l’impresa sceglie quella combinazione di fattori, definita dalle quantità acquistate degli input, che rende minimo il costo totale da sostenere per produrre un data quantità di beni. Tale c. totale è costituito dall’insieme delle spese che l’impresa affronta per produrre una data quantità di prodotto, tipicamente rappresentato dall’acquisto dei servizi dei fattori produttivi. Per definizione, questi c. sono minimi quando non è possibile spostare denaro dall’acquisto di un servizio di un fattore (o semplicemente di fattore) a un altro, in modo da ridurli. Pertanto, la minimizzazione implica che i c. marginali dei diversi fattori siano tra loro uguali. Per verificare questa condizione e determinare la combinazione dei fattori che minimizza i c. di produzione, si può procedere con un grafico, utilizzando la funzione di produzione (➔ produzione, funzione di) e i prezzi dei fattori. La funzione di produzione, permette di rappresentare nel piano dei fattori (x1, x2), attraverso un isoquanto (➔), le combinazioni dei fattori che danno luogo a una medesima quantità di prodotto. Per dati prezzi dei fattori, il c. totale di produzione è rappresentato dalla retta di isocosto (➔). La combinazione di minimo c. è data dal più alto isoquanto coerente con un dato isocosto, dunque dal punto di tangenza tra isoquanto e isocosto (punto P nel grafico). In P, la combinazione di minimo c. è caratterizzata dall’uguaglianza tra la pendenza dell’isocosto e quella dell’isoquanto. Se i prezzi degli input sono rispettivamente w1 e w2, la pendenza dell’isocosto (in valore assoluto) è data dal rapporto fra i prezzi dei due fattori
La pendenza dell’isoquanto è data dal Saggio Marginale di Sostituzione (SMS; ➔ saggio), ossia dal rapporto dei prodotti marginali dei due fattori (sempre in valore assoluto). Se la funzione di produzione è genericamente rappresentabile in forma analitica, come f(x1,x2), il SMS è uguale a
Il punto di minimo c. (x*1,x*2) è perciò caratterizzato dalla seguente condizione:
Per comprendere il significato intuitivo di questa condizione di ottimo, si può riscriverla nel seguente modo:
Ciascun lato di questa uguaglianza rappresenta un c. marginale: il lato di sinistra il c. marginale del fattore 1, quello di destra il c. marginale del fattore 2. Se tale condizione non fosse verificata (per es., se il c. marginale del fattore 1 fosse minore di quello del fattore 2), si potrebbe ridurre il c. totale di produzione, spostando la spesa verso l’acquisto di quel fattore il cui c. marginale è minore (nell’esempio, dal fattore 2 al fattore 1).