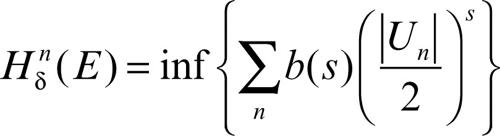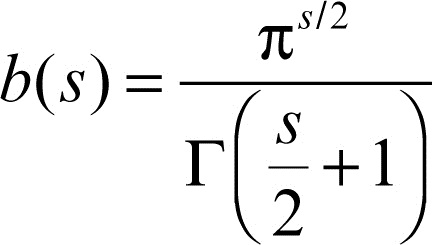Hausdorff, misura di

Hausdorff, misura di

Hausdorff, misura di valore numerico non negativo, che può anche essere ∞, che si attribuisce a un insieme E ⊆ Rⁿ, introdotto da F. Hausdorff. Per la sua definizione, si considera un δ-ricoprimento di E {U_n}_n ∈ N nel seguente modo:

• U_n ≠ ∅

• |U_n| = sup {|x – y| : x, y ∈ U_n} ≤ δ

Dato s ∈ R⁺, per ogni δ > 0 si considera

dove {U_n}_n∈N è un δ-ricoprimento di E mentre

Si definisce misura di Hausdorff s-dimensionale Hⁿ(E) il limite per δ → 0 di H_δⁿ(E). Si osservi che il limite esiste sempre e, se s è intero, allora b(s) rappresenta il volume della palla unitaria in Rⁿ. Se l’insieme E è vuoto, la sua misura di Hausdorff è 0 e se un insieme è strettamente contenuto in un altro, la sua misura di Hausdorff è minore o uguale a quella dell’insieme che lo contiene.