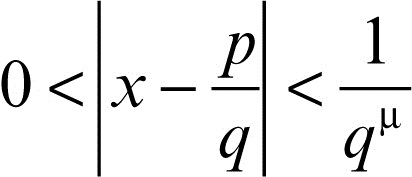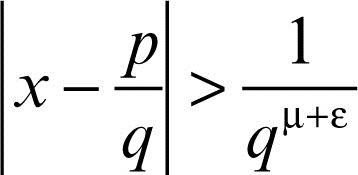irrazionalita, misura di

irrazionalita, misura di

irrazionalità, misura di per un numero reale x, indicato con R l’insieme dei reali positivi μ tali che il sistema di disequazioni

con p e q interi, ha al più un numero finito di soluzioni, la misura di irrazionalità di x (detta anche costante di Liouville-Roth) è il valore μ(x) a cui tende l’approssimazione di → Liouville delle precedenti disuguaglianze e x non è ulteriormente approssimabile con numeri razionali:

(indicando con

l’estremo inferiore). Se l’insieme R è vuoto, allora μ(x) = ∞ per definizione e x è detto numero di → Liouville. Per R non vuoto si può avere:

• μ(x) = 1 se x è razionale;

• μ(x) = 2 se x è irrazionale algebrico di grado > 1;

• μ(x) ≥ 2 se x è irrazionale trascendente.

Si noti che il caso μ(x) = 2 può corrispondere sia a x algebrico di grado maggiore di 1, sia a x trascendente. Per aver dimostrato la possibilità che il numero x sia algebrico di grado maggiore di 1, nel caso μ(x) = 2, K.F. Roth ha ottenuto la Medaglia Fields nel 1958. Il numero aureo ha misura d’irrazionalità 2.

Se x irrazionale ha misura d’irrazionalità μ, allora μ è il più piccolo numero tale che la disuguaglianza

è vera per ogni ε > 0 e per ogni p e q sufficientemente grandi.