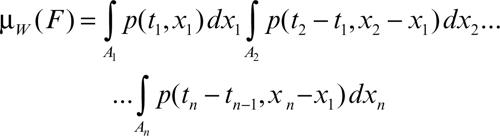Wiener, misura di

Wiener, misura di

Wiener, misura di misura che esprime la probabilità che una particella, nel moto browniano, a dati istanti t₁, t₂, ..., t_n si trovi all’interno di dati insiemi A₁, A₂, ..., A_n. Tale misura è definibile sullo spazio delle funzioni continue a valori reali su un intervallo chiuso [a, b], a partire da un insieme di punti arbitrari dell’intervallo, indicati con t₁, t₂, ..., t_n, tali che 0 < t₁ < t₂ < ... < t_n < 1 e da un insieme di sottoinsiemi boreliani A₁, ..., A_n (→ Borel, insiemi di) della retta reale. Considerato l’insieme

di tutte le funzioni ƒ: [0, 1] → R tali che, per

si abbia ƒ(t_k) ∈ A_k, la misura di Wiener di F è così definita:

dove p(t, x) è la densità di probabilità per la posizione x di una particella a un fissato tempo t e si ha: