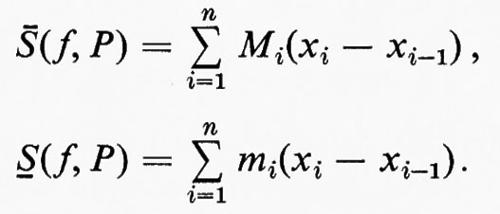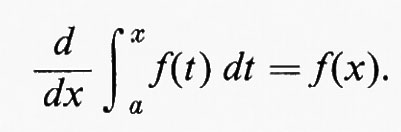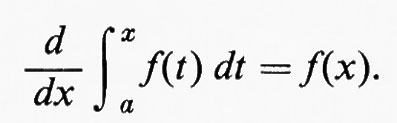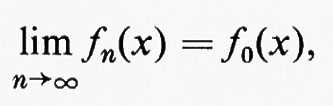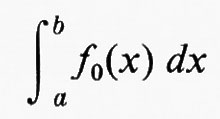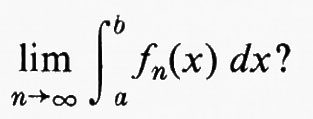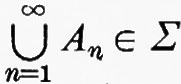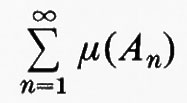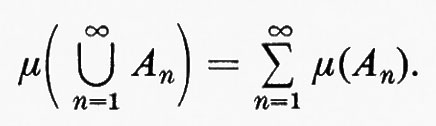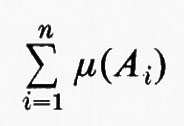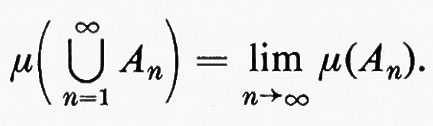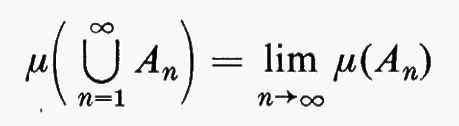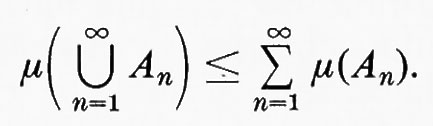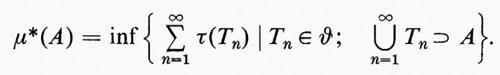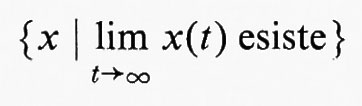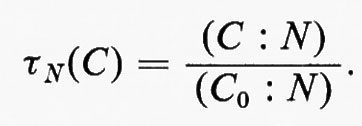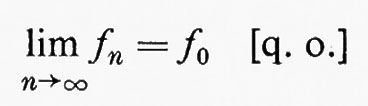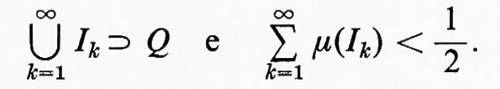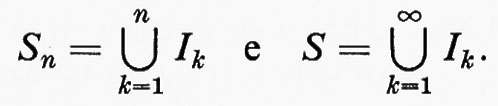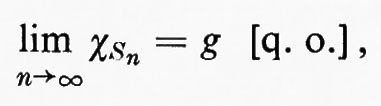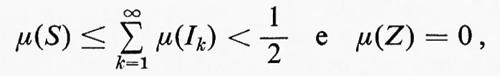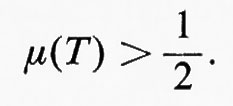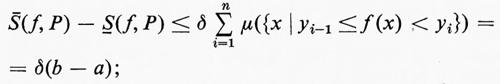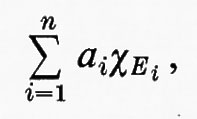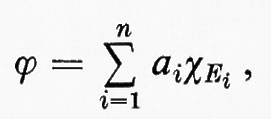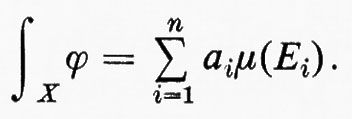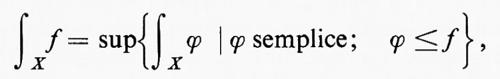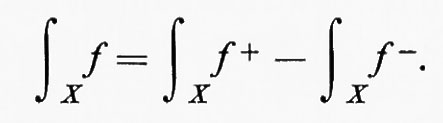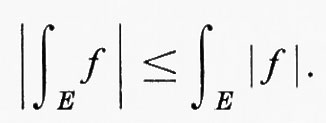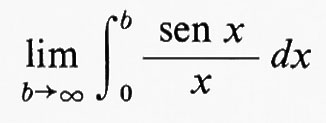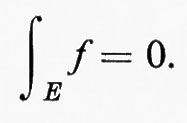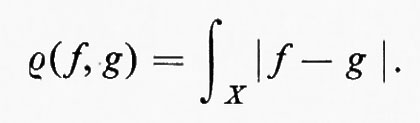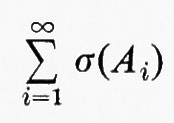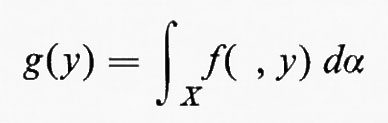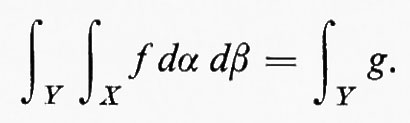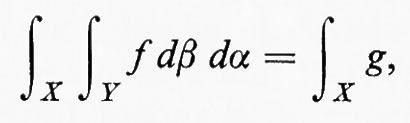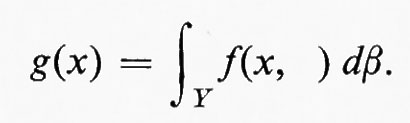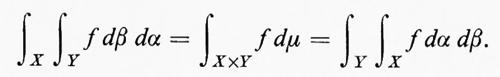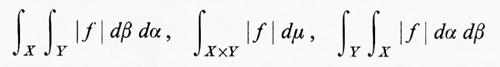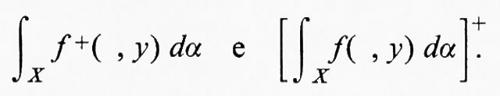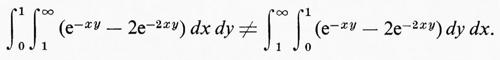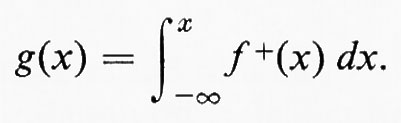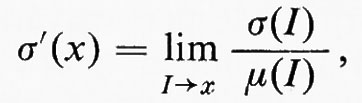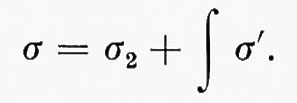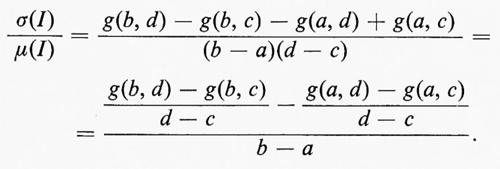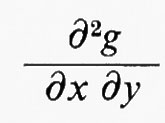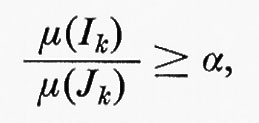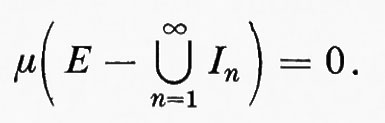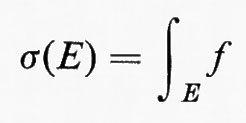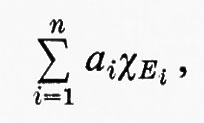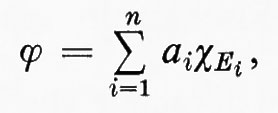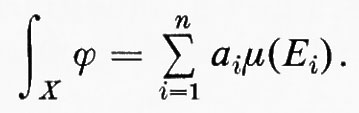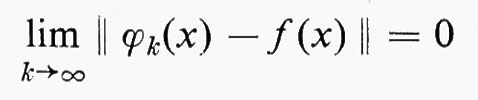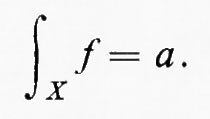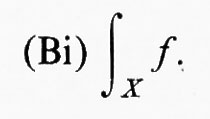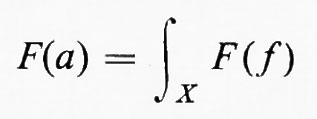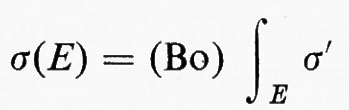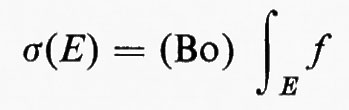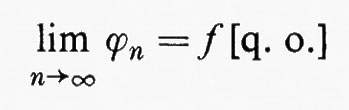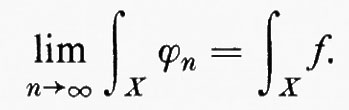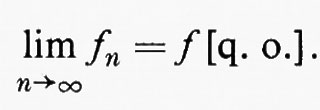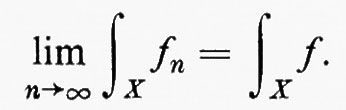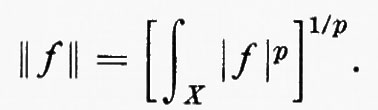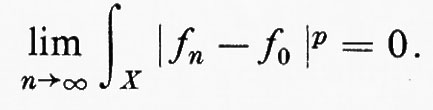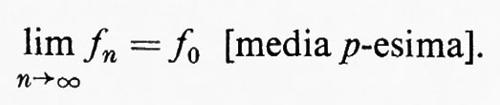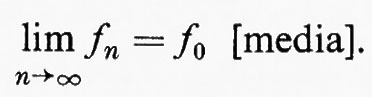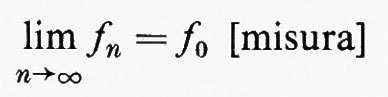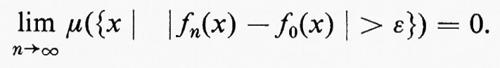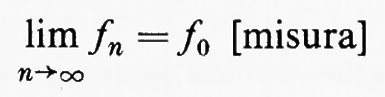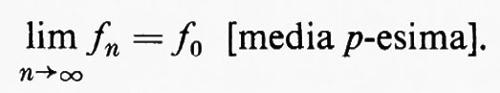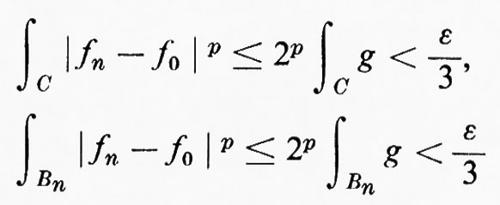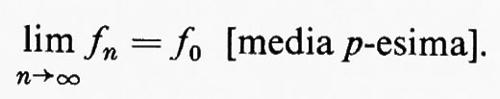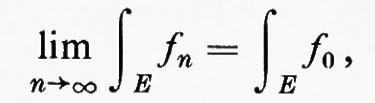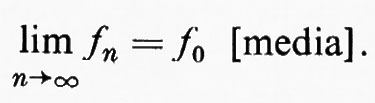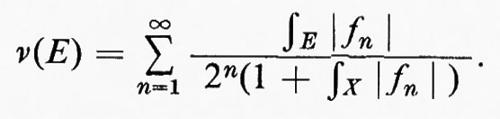Misura e integrazione

Misura e integrazione

Introduzione

La nozione di integrale viene spesso introdotta considerando il problema di determinare l'area racchiusa da una curva, prendendo un limite di somme di aree di rettangoli. Più in generale, si può dire che si comincia con figure la cui area è nota e si istituisce un procedimento di passaggio al limite per trovare altre aree. In questa forma la storia dell'integrazione risale all'antica Grecia. Eudosso formulò il ‛metodo di esaustione' e Archimede lo applicò con successo a numerosi problemi di aree e di volumi.

L'integrazione divenne uno strumento della matematica quando, verso la fine del Seicento, Newton e Leibniz scoprirono, indipendentemente l'uno dall' altro, che l'integrazione e la differenziazione sono operazioni l'una inversa dell'altra, vale a dire

Questa è la chiave per il calcolo di integrali mediante l'uso di formule di antiderivazione.

Nel XVIII secolo il calcolo si sviluppò senza che venisse prestata molta attenzione a problemi di rigore. Il XIX secolo vide lo sviluppo dei fondamenti del calcolo. All'inizio del secolo venne definito in modo soddisfacente il concetto di limite e circa cinquant'anni più tardi nacque la seguente definizione di integrale. Sia f una funzione limitata su [a, b] e sia P una partizione di [a, b] individuata dall'insieme

{x_i∣i=0,1,2 ..., n},

ove

a=x₀〈x₁〈x₂〈...〈x_n=b.

Sia

m_i=inf {f(x)∣x_i-1≤x≤x_i}

e

M_i=sup {f(x)∣x_i-1≤x≤x_i}.

Definiamo le somme inferiori e superiori rispetto a P per f mediante le

Si può dimostrare che per due qualsiasi partizioni P e Q si ha

-S(f,P)≤Ô(f,Q);

così che, se π è l'insieme di tutte le partizioni di [a,b], risulta

sup {-S(f, P)∣P∈π}≤inf {Ô(P)∣P∈π}.

Se l'estremo superiore delle somme inferiori uguaglia l'estremo inferiore delle somme superiori, il loro valore comune si indica con

e si dice che f è integrabile su [a, b].

Il procedimento precedente definisce quello che è noto come l'integrale di Riemann, sebbene i dettagli che abbiamo esposto qui differiscano in qualche misura da quelli a suo tempo dati da Riemann. Verso la fine dell'Ottocento il sistema dei numeri reali era ormai ben compreso e questo condusse a una dimostrazione rigorosa del fatto che, se f è limitata e continua a tratti su [a, b], essa è integrabile secondo Riemann su [a, b]. Venne anche dimostrato che, se f è integrabile secondo Riemann su [a, b] e continua nel punto x∈(a, b), risulta

Nel 1900 dunque si poteva disporre di una definizione precisa di integrale, di un teorema maneggevole che dava condizioni sufficienti per l'integrabilità e di un teorema ragionevole che caratterizzava la differenziazione e l'integrazione come procedimenti l'uno inverso dell'altro. Questa situazione spinse ovviamente a proseguire nella ricerca di condizioni necessarie per l'integrabilità e di conoscenze più precise sulla differenziabilità dell'integrale. Indipendentemente da queste esigenze, tuttavia, la teoria poteva considerarsi già sufficientemente completa.

Molto prima del 1900, tuttavia, era sorto un altro problema importante che aveva seriamente messo in dubbio la convenienza della definizione di integrale di Riemann. Per meglio chiarire questo punto, rifacciamoci alle ricerche iniziali di Archimede. Questi conosceva le formule per le aree di certe figure a contorni rettilinei e le usava come approssimazioni per trovare formule esatte per il calcolo di aree di figure a contorni curvilinei. Perché non servirsi delle formule di aree già note per trovarne altre, approssimate, per nuove figure? Col linguaggio degli integrali di funzioni, questa questione si può porre nella forma seguente: se

è noto per n=1, 2, 3, ... e se

si può calcolare

come

Gli analisti della fine dell'Ottocento ben sapevano che, anche se tutte le f_n sono integrabili secondo Riemann e anche se f₀ è limitata, può benissimo accadere che f₀ non sia integrabile secondo Riemann. Cosi, nel 1900, la teoria dell'integrazione secondo Riemann era virtualmente completa, ma non poteva considerarsi soddisfacente in quanto la classe delle funzioni integrabili non era chiusa rispetto all'operazione di passaggio al limite.

Nel 1906 la teoria dell'integrazione ebbe nuovo impulso con la comparsa dell'integrale di Lebesgue. Scopo di questo articolo è quello di indicare sommariamente tutti gli sviluppi della teoria realizzati nel nostro secolo. Lo schema dell'articolo si basa su idee già menzionate in questa introduzione. Il cap. 2 presenta le idee fondamentali per la definizione dell'integrale di Lebesgue; il È b è particolarmente interessante in quanto contiene gli elementi essenziali per dimostrare che la classe delle funzioni integrabili secondo Lebesgue è chiusa rispetto a un'opportuna operazione di passaggio al limite. Il cap. 3 si occupa dell'integrazione e della differenziazione come processi inversi l'uno dell'altro. Disponendo ora di un numero di funzioni maggiore di quello delle funzioni integrabili secondo la teoria di Riemann, la differenziabilità dell'integrale diventa un problema più complicato, ma la teoria di Lebesgue offre una soluzione precisa. Il cap. 4 tratta delle ricerche, effettuate fra il 1930 e il 1950, relative al caso in cui le funzioni integrabili non hanno valori reali, bensì, più in generale, valori in uno spazio di Banach. Il cap. 5, infine, riassume i teoremi di convergenza, i quali mostrano precisamente come la teoria di Lebesgue riesca a evitare gli aspetti insoddisfacenti della teoria di Riemann, quando si considerino integrali di limiti.

L'esposizione, anziché cronologica, è per argomenti, allo scopo di dare un quadro dell'intera teoria come essa appare a settant'anni dalla sua nascita.

L'integrale di Lebesgue

Misure esterne e misure

Diamo anzitutto una definizione fondamentale. Sia X un insieme e Σ una classe di sottoinsiemi di X; in tal caso, si dice che Σ è una ‛σ-algebra' se sono soddisfatte le seguenti condizioni: a) l'insieme vuoto appartiene a Σ (cioè 0/ ∈Σ); b) se un insieme A è elemento di Σ, allora l'insieme complementare X−A, che indicheremo con −A, appartiene anch'esso a Σ (cioè A∈Σ implica −A∈Σ); c) l'insieme che si ottiene come unione di un'infinità numerabile di elementi di Σ appartiene anch'esso a Σ (cioè A_n∈Σ, per n=1, 2, 3, ..., implica

Il sistema esteso dei numeri reali consta dei numeri reali ai quali si siano aggiunti due punti ideali chiamati +∞ e −∞. Si tratta di un insieme ordinato linearmente dalla regola: −∞〈x〈∞, per tutti gli x reali. Si completa la struttura algebrica ponendo, per ogni numero reale x, x−∞=−∞ e x+∞=∞. Di proposito, tuttavia, vengono lasciati indefiniti ∞−∞ e 0•∞.

Una funzione μ da una σ-algebra Σ a un sistema esteso di numeri reali si chiama numerabilmente additiva se, per ogni successione disgiunta {A_n} di insiemi di Σ, la somma

è definita nel sistema esteso dei numeri reali e se

Se per ogni insieme finito {A₁, A₂, ..., A_n} di insiemi disgiunti di Σ

si dice che μ è finitamente additiva.

La differenza tra l'additività finita e l'additività numerabile può essere descritta ricorrendo alla condizione di continuità. Se, per ogni n, A_n⊂A_n+1, {A_n} si chiama successione crescente di insiemi. Se μ è numerabilmente additiva su Σ e {A_n} è una qualsiasi successione crescente di Σ, risulta

Questo si chiama teorema del limite per una successione crescente. Altrettanto importante è un inverso parziale. Se μ è finitamente additiva su una σ-algebra Σ e se

per ogni successione crescente {A_n} di Σ, μ è numerabilmente additiva.

Una funzione numerabilmente additiva non negativa si chiama funzione misura. Si può dimostrare che una funzione misura gode di due proprietà utili. È monotona, cioè, se A∈Σ, B∈Σ e A⊂B, risulta μ(A)≤μ(B) ed è numerabilmente subadditiva, cioè, se {A_n} è una qualsiasi successione di insiemi di Σ, risulta

Il teorema di decomposizione di Jordan afferma che ogni funzione numerabilmente additiva è la differenza di due funzioni misura.

Nella sua definizione dell'integrale, Lebesgue si servì di una funzione misura. Un aspetto importante della teoria generale è la ricerca di metodi per la costruzione di specifiche funzioni misura. Un modo di ottenerle poggia sulle misure esterne. Sia ancora X un qualsiasi insieme. Una funzione μ^* dalla classe di tutti i sottoinsiemi di X al sistema esteso dei numeri reali si chiama misura esterna se essa è monotona, è numerabilmente subadditiva e si annulla sull'insieme vuoto. Se μ^* è una misura esterna sui sottoinsiemi di X, un insieme E⊂X si chiama μ^*-misurabile se

μ^*(A)=μ^*(A⋂E)+μ^*(A−E)

per ogni A⊂X. Grosso modo un insieme misurabile e il suo complementare decompongono ogni insieme in modo tale che la misura esterna risulti additiva.

Teorema: se μ^* è una misura esterna e Σ è la classe degli insiemi μ^*-misurabili, Σ è una σ-algebra e la restrizione di μ^* a Σ è una misura.

Questo teorema mostra che misure esterne danno luogo a misure. Resta il problema di costruire misure esterne specifiche. Supponiamo per esempio che X sia il sistema dei numeri reali; come si potrà descrivere esplicitamente una funzione con le proprietà di una misura esterna sulla classe di tutti gli insiemi di numeri reali? Il procedimento abituale consiste nel considerare inizialmente una classe relativamente piccola di insiemi sulla quale sia possibile costruire una funzione mediante una formula esplicita e quindi utilizzare questa funzione più piccola per costruire una misura esterna. I dettagli di questo procedimento si possono descrivere in una situazione molto generale. Sia X un qualsiasi insieme e sia ϑ una qualsiasi classe di sottoinsiemi di X tale che 0/ ∈ϑ. Sia τ una qualsiasi funzione non negativa da ϑ al sistema esteso dei numeri reali, tale che τ(0/ )=0. Per ogni A⊂X poniamo per definizione

Una funzione μ^* definita in questo modo è sempre una misura esterna. Grosso modo questo procedimento consiste nel prendere certi insiemi semplici, attribuire a essi dei pesi, quindi considerare ricoprimenti numerabili di insiemi arbitrari mediante insiemi semplici e infine prendere l'estremo inferiore dei pesi dei ricoprimenti.

Sia X la retta reale e sia ϑ la classe degli intervalli aperti. Dato un intervallo aperto, indichiamo con τ la sua lunghezza. Il procedimento che abbiamo menzionato dianzi definisce una funzione μ^*, che viene chiamata misura esterna di Lebesgue sulla retta reale. Essa determina una σ-algebra di insiemi misurabili secondo Lebesgue e la restrizione μ di μ^* a questa σ-algebra prende il nome di misura di Lebesgue sulla retta reale. Calcoli diretti mostrano che μ^*=τ sugli intervalli aperti, cioè μ^* definisce le lunghezze sugli intervalli aperti generalizzando così il concetto di lunghezza a insiemi arbitrari di numeri reali. Per avere una visione più chiara della misura stessa (in particolare della classe degli insiemi misurabili) sarà utile far riferimento a considerazioni topologiche.

Sia (X, ρ) uno spazio metrico. Gli insiemi di Borel sono definiti dalla condizione che essi formino la più piccola σ-algebra contenente gli insiemi aperti. Una misura esterna μ^* definita sui sottoinsiemi di X si chiama misura esterna metrica se μ^*(A⋃B)=μ^*(A)+μ^*(B) ogniqualvolta ρ(A, B)>0.

Teorema: se μ^* è una misura esterna metrica, tutti gli insiemi di Borel sono μ^*-misurabili.

Si può dimostrare mediante un calcolo diretto che la misura esterna di Lebesgue è metrica; pertanto tutti gli insiemi di Borel sulla retta reale sono misurabili secondo Lebesgue. La misura di Lebesgue è dunque una generalizzazione numerabilmente additiva della nozione di lunghezza a un ampia classe di insiemi diversi dagli intervalli. Esistono degli insiemi misurabili secondo Lebesgue, che non sono insiemi di Borel, ma ogni insieme misurabile secondo Lebesgue differisce da un insieme di Borel per un insieme di misura (di Lebesgue) nulla. È stato dimostrato che l'esistenza di insiemi non misurabili secondo Lebesgue è logicamente equivalente all'assioma della scelta.

Mediante il procedimento indicato dianzi si possono costruire molte altre misure specifiche. In generale, tutto ciò che si richiede per definire una misura specifica è una classe ϑ e una funzione τ. Sia f una funzione a valori reali sulla retta reale, monotona e continua a destra. Sia ϑ la classe degli intervalli aperti e poniamo τ[(a, b)]=f(b)−f(a). La misura che ne risulta si chiama misura di Lebesgue-Stieltjes generata da f.

Per ottenere un altro esempio, sia f una funzione a valori reali sul piano. Sia ϑ l'insieme dei rettangoli aperti con lati paralleli agli assi coordinati. Per il rettangolo aperto

I={(x, y)∣a〈x〈b, c〈y〈d}

poniamo

τ(I)=f(b, d)−f(b, c)−f(a, d)+f(a, c).

Supponiamo che f sia continua a destra in ciascuna variabile separatamente e tale che la τ definita dianzi sia sempre non negativa. La misura che ne risulta si chiama ancora misura di Lebesgue-Stieltjes generata da f. Se f(x, y)=xy, la misura corrispondente è la misura di Lebesgue nel piano ed è una generalizzazione dell'area.

Consideriamo una misurazione che dipenda dal tempo e che sia governata dal caso e indichiamo con x(t) la misurazione al tempo t. Se X è l'insieme di tutte le funzioni a valori reali su [0, ∞), X rappresenta l'insieme di tutti i possibili tipi di comportamento per le misurazioni dipendenti dal tempo e si ottiene un processo stocastico continuo assegnando delle probabilità a opportuni insiemi in X. Ciò si ottiene definendo una misura mediante il procedimento descritto dianzi. Sia ϑ la classe di tutti i sottoinsiemi di X della forma

{x∣a_i〈x(t_i)〈b_i; i=1, 2, ..., n}

e, su un tale insieme, sia τ la probabilità che in ciascuno dei tempi t₁, t₂, ..., t_n la misurazione soddisfi le disuguaglianze indicate. Il procedimento usuale fornisce ora una misura di probabilità su una certa σ-algebra in X. Tuttavia questa misura non è in generale completamente soddisfacente, in quanto

non è misurabile. La soluzione finale di questo problema consiste anzitutto nel costruire una misura insoddisfacente con il metodo or ora indicato e poi nell'approntare un procedimento molto complicato con il quale questa misura si estende a una σ-algebra più grande che comprende gli insiemi definiti dai limiti.

Sia X un gruppo topologico localmente compatto. Una misura μ su una σ-algebra Σ in X si chiama misura di Haar a sinistra (o invariante a sinistra) se Σ contiene tutti gli insiemi compatti, μ non è identicamente uguale a zero ed è finita sugli insiemi compatti e μ(xE)=μ(E) per tutti gli x∈X e tutti gli E∈Σ (in altre parole μ è invariante rispetto alle traslazioni a sinistra). Si dimostra che ogni gruppo topologico localmente compatto ha una misura di Haar e in tale dimostrazione si utilizza lo stesso metodo di costruzione di tutti gli altri esempi di cui abbiamo parlato finora. La classe ϑ consiste dell'insieme di tutti gli insiemi aperti con chiusura compatta. In questo caso però la definizione di τ è più complicata. Eccola in breve: sia N un intorno dell'identità e sia C un compatto. Definiamo (C:N) come il minimo numero di traslati sinistri di N che coprono C. Prendiamo per riferimento un insieme compatto prefissato C₀ e poniamo per definizione

In un certo senso τ_N(C) dà le misure relative di C e C₀, quando N sia l'ampiezza della maglia del procedimento di misurazione. Un passaggio al limite trasfinito permette di eliminare la dipendenza da N e di ottenere così un risultato τ₀(C) che misura più precisamente le dimensioni relative di C e di C₀.

Infine, se G è aperto e ha misura compatta, poniamo per definizione

τ(G)=sup{τ₀(C)∣C⊂G; C compatto}.

Utilizzando ϑ e τ nel solito modo, si ottiene una misura di Haar invariante a sinistra.

Uno spazio di misura è una terna (X, Σ, μ) costituita da un insieme X, da una σ-algebra Σ di sottoinsiemi di X e da una misura μ definita su Σ. Molti concetti della teoria dell'integrazione del XX secolo possono essere definiti in funzione di arbitrari spazi di misura e quindi possono essere applicati a uno qualsiasi degli esempi fin qui ricordati e anche a molti altri. Alcuni aspetti della teoria concernono però questioni più particolari.

b) Funzioni misurabili

Sia (X, Σ, μ) uno spazio di misura e sia f una funzione a valori reali su X. Se A è un qualsiasi insieme di numeri reali, la sua immagine inversa rispetto a f è

f^-1(A)={x∣f(x)∈A}.

Se, per ogni insieme aperto G di numeri reali, si ha

f^-1(G)∈Σ,

si dice che f è una funzione misurabile.

Si può mostrare che ciascuna delle condizioni seguenti è equivalente alla misurabilità di f: a) {x∣f(x)〈a}∈Σ per ogni a reale; b) {x∣f(x)≤a}∈Σ per ogni a reale; c) {x∣f(x)>a}∈Σ per ogni a reale; d) {x∣f(x)≥a}∈Σ per ogni a reale. Spesso una di queste viene presentata come definizione di funzione misurabile. Poichè gli insiemi misurabili formano una σ-algebra, la misurabilità di certe immagini inverse implica facilmente quella di molte altre. Infatti, se f è una funzione misurabile e B è un insieme di Borel nel sistema dei numeri reali, f^-1(B) è un insieme misurabile.

Se X è la retta reale e f è continua, per ogni insieme aperto G, f^-1(G) è aperto e quindi misurabile secondo Lebesgue. Pertanto tutte le funzioni continue sulla retta reale sono misurabili secondo Lebesgue. È chiaro che anche molte funzioni discontinue sono misurabili secondo Lebesgue. Per esempio, sia Q l'insieme dei numeri razionali e sia χ_Q la funzione caratteristica definita da

Questa funzione è discontinua dovunque, ma poiché Q è un insieme di Borel, e quindi è misurabile secondo Lebesgue, χ_Q è una funzione misurabile secondo Lebesgue.

Se P(x) è una proposizione riguardante un punto x in uno spazio di misura e se

μ({x∣P(x) è falsa})=0,

si dice che P è vera quasi ovunque (q.o.). Questa situazione si può descrivere anche dicendo che P(x) è vera per quasi tutti gli x.

Forse l'uso più importante del concetto di q. o. è legato ai limiti. Se {f_n} è una successione di funzioni a valori reali su uno spazio di misura, l'enunciato

significa che esiste un insieme A tale che μ(−A)=0 e {f_n} converge puntualmente a f₀ su A.

Teorema: sia (X, Σ, μ) un qualsiasi spazio di misura. Se {f_n} è una successione di funzioni misurabili su X e se

f₀ è una funzione misurabile.

Già nell'introduzione abbiamo osservato come la maggiore debolezza della teoria dell'integrazione di Riemann consista nel fatto che, anche per funzioni limitate, l'integrabilità si conserva difficilmente quando si passa a limiti puntuali. Il teorema precedente è il punto chiave per eliminare questa manchevolezza dalla teoria di Lebesgue. La dimostrazione del teorema del limite q. o. non è affatto difficile, ma dipende dal fatto che Σ è chiusa rispetto a unioni numerabili.

Lebesgue scoprì la seguente condizione necessaria e sufficiente perché una funzione limitata f su [a, b] sia integrabile secondo Riemann: f deve essere continua q. o. D'altra parte (v. cap. 2, È c) una funzione limitata è integrabile secondo Lebesgue su [a, b] se, e soltanto se, essa è misurabile. La differenza fondamentale fra le due teorie nasce dal fatto che la misurabilità si conserva nei passaggi al limite q. o., mentre ciò non avviene per la continuità q. o. La differenza è evidente nell'esempio seguente.

Sia μ la misura di Lebesgue sulla retta reale e sia Q l'insieme dei numeri razionali in [0, 1]. Poiché Q è numerabile, si vede facilmente che μ(Q)=0. Esiste pertanto una successione di intervalli aperti {I_k} tale che

Ora, sia

Ciascuna funzione caratteristica χ_Sn è integrabile secondo Riemann, in quanto essa ha un numero finito di discontinuità. Tuttavia, se

allora g=χ_S[q. o.], e l'argomentazione seguente mostra che g non è integrabile secondo Riemann. Sia Z l'insieme di misura zero su cui g≠χ_S e sia T=([0, 1]−S). Essendo

allora

Sia x∈T; risulta

g(x)=χ_S(x)=0.

Sia I un intervallo aperto contenente x. Poiché I contiene numeri razionali, esso interseca S in un insieme aperto non vuoto; esiste dunque un intervallo aperto J⊂I⊂S. Ora, J−Z è non vuoto, in quanto J ha misura positiva e Z ha misura nulla; esiste perciò un punto y∈J−Z⊂(I⋂S)−Z e

g(y)=χ_S(y)=1.

Pertanto g è discontinua in ciascun punto x dell'insieme T di misura positiva e quindi non è integrabile secondo Riemann.

c) Definizione di integrale

Sia μ la misura di Lebesgue sulla retta reale e sia f una funzione misurabile limitata su [a, b] con c≤f(x)〈d per x∈[a, b]. Sia P una partizione di [c, d] individuata dall'insieme {y_i∣i=0, 1, 2, ..., n}; formiamo le somme superiori e inferiori nel modo seguente:

Ora, se y_i−y_i-1≤δ per ogni i, risulta

cosicché l'estremo inferiore delle somme superiori è uguale all'estremo superiore delle somme inferiori. Questo valore comune dell'estremo superiore e dell'estremo inferiore è l'integrale di Lebesgue di f su [a, b].

Daremo in seguito una definizione molto più ampia di integrale, ma, prima, confrontiamo il poco che abbiamo visto dell'integrale di Lebesgue con l'integrale di Riemann. Nella costruzione di Riemann si suddivide l'intervallo [a, b] e, perché non vi siano lacune fra l'insieme delle somme superiori e quello delle somme inferiori, occorre porre una condizione di continuità. Nella definizione di Lebesgue che abbiamo visto ora, è proprio l'intervallo [c, d], invece, che viene suddiviso, restando con ciò automaticamente esclusa la possibilità che tali lacune esistano. Tuttavia, per stabilire la definizione di Lebesgue, sono necessari due fatti che non compaiono affatto nella teoria di Riemann: 1) un modo per fissare la misura per gli insiemi {x∣y_i-1≤f(x)〈y_i}; 2) l'additività di questa misura. La teoria della misura e il concetto di funzione misurabile forniscono questi due elementi.

La definizione di integrale data dianzi è essenzialmente quella introdotta da Lebesgue nel 1906. Esposizioni più recenti della teoria dell'integrazione utilizzano le seguenti considerazioni. Servendosi della teoria della misura, è possibile definire somme superiori e inferiori per funzioni misurabili in modo tale che non vi sia nessuna lacuna fra i due sistemi di somme. Pertanto ci si può liberare delle somme superiori e l'integrabilità di una funzione misurabile può essere definita soltanto mediante condizioni di limitatezza intrinseche a qualsiasi teoria di integrazione; in particolare, condizioni di limitatezza che garantiscano che gli integrali abbiano valori finiti.

Questo modo di procedere può essere attuato così: sia (X, Σ, μ) un qualsiasi spazio di misura. Una funzione semplice è una funzione del tipo

ove gli E_i sono insiemi misurabili di misura finita. Con la condizione che, se i≠j, siano E_i⋂E_j=0/ e a_i≠a_j, la rappresentazione di una data funzione semplice come combinazione lineare di funzioni caratteristiche è unica. Ora, se

poniamo per definizione

Successivamente, sia f una qualsiasi funzione misurabile non negativa e, per definizione, si ponga

purché questo estremo superiore sia finito. Se l'estremo superiore è infinito, f non è integrabile. Si osservi che qui non si richiede che f sia limitata e che X abbia misura finita. Questa definizione è valida per tutti i casi allo stesso tempo. Sia infine f una qualsiasi funzione misurabile e poniamo per definizione

Chiaramente f⁺ e f^- sono funzioni misurabili non negative e f⁺−f^-=f; si dice che f è integrabile quando f⁺ e f^- sono ambedue integrabili e in tal caso si pone

Se f è una funzione misurabile ed E è un insieme misurabile, f è integrabile su E se fχ_E è integrabile e l'integrale di f su E è definito dalla

Vale la pena di osservare che la precedente definizione di integrale di una funzione reale su uno spazio di misura ha molte varianti nella letteratura matematica. Di fatto esistono altrettante definizioni di integrale quanti sono i libri sulla misura e l'integrazione. Tuttavia, per le funzioni a valori reali, queste definizioni sono tutte equivalenti, nel senso che tutte forniscono la stessa classe di funzioni integrabili e attribuiscono tutte gli stessi valori agli integrali. Per funzioni a valori in spazi più generali questa equivalenza fra le definizioni non sussiste più (v. sotto, cap. 4).

Poichè f⁺+f^-=∣f∣, la condizione che f⁺ e f^- siano ambedue integrabili affinché lo sia anche f conduce al risultato che, se f è integrabile, anche ∣f∣ lo è. A tale proposito è importante la disuguaglianza

L'integrale di Lebesgue generalizza l'integrale di Riemann, nel senso che, se una funzione ha un integrale di Riemann, essa ha anche un integrale di Lebesgue e i due integrali sono uguali. Tuttavia, come abbiamo notato dianzi, la proprietà di integrabilità assoluta fa parte integrante della definizione di Lebesgue e per questa ragione l'integrale di Lebesgue non è una generalizzazione dell'integrale di Cauchy-Riemann (l'integrale improprio del XIX secolo). Per esempio

è finito, ma

così (senx)/x è integrabile secondo Cauchy-Riemann su [0, ∞), ma non è integrabile secondo Lebesgue sullo stesso intervallo.

Teorema: se g è integrabile, f è misurabile e ∣f∣≤∣g∣ q. o., allora f è integrabile.

Vale la pena di mettere in evidenza questo teorema piuttosto semplice, in quanto esso indica un metodo pratico per determinare l'integrabilità e, cosa ancora più importante, indica chiaramente le due condizioni indipendenti che assicurano l'integrabilità. Una funzione, per essere integrabile, deve essere abbastanza liscia e abbastanza piccola. Le teorie di Lebesgue e Riemann differiscono anzitutto per i criteri concernenti la prima delle due caratteristiche: nella teoria di Lebesgue il criterio è la misurabilità, mentre in quella di Riemann è la continuità quasi ovunque. Per gli integrali assolutamente convergenti i criteri di grandezza sono gli stessi in ambedue le teorie.

d) Proprietà dell'integrale

Se f è una qualsiasi funzione misurabile e μ(E)=0, risulta

Lo spazio L₁ delle funzioni integrabili è uno spazio metrico rispetto alla distanza

Alla luce di quanto abbiamo detto a proposito degli integrali su insiemi di misura nulla, è chiaro che questa è una pseudometrica e che, per la relazione di equivalenza ρ(f, g)=0, la classe di equivalenza contenente f è l'insieme di tutte le funzioni uguali a f q. o. Grosso modo, funzioni uguali q. o. sono equivalenti nella teoria dell'integrazione di Lebesgue.

Teorema: se f è integrabile e σ è definita dalla

σ è una funzione numerabilmente additiva sulla classe Σ degli insiemi misurabili.

Questo teorema dipende dalla integrabilità assoluta intimamente legata alla definizione dell'integrale di Lebesgue. Se fossero ammessi integrali impropri condizionatamente convergenti, ci sarebbero delle successioni disgiunte {A_i} per le quali la somma

non sarebbe definita nel sistema esteso dei numeri reali.

Sia (X, Σ, μ) un qualsiasi spazio di misura e sia σ un'altra funzione su Σ. La funzione σ è assolutamente continua rispetto a μ se, dato un qualsiasi ε>0, esiste un δ>0 tale che μ(E)〈δ implica ∣σ(E)∣〈ε. Se σ è finita dappertutto ed è numerabilmente additiva, essa è assolutamente continua rispetto a μ se, e soltanto se, μ(E)=0 implica σ(E)=0. Quest'ultima condizione viene spesso data come una definizione di continuità assoluta, ma quella che abbiamo esposto prima è più utile, in quanto si generalizza nella definizione di continuità assoluta uniforme di una successione di funzioni. Incontreremo questo concetto nel cap. 5.

Se f è integrabile e

chiaramente σ è assolutamente continua. È possibile invertire parzialmente questo enunciato facendo una piccola restrizione sullo spazio di misura. Uno spazio di misura (X, Σ, μ) si chiama σ-finito se X è unione di una famiglia numerabile di misura finita.

Teorema di Radon-Nikodym: se (X, Σ, μ) è uno spazio di misura σ-finita e se σ è una funzione su Σ finita dappertutto, numerabilmente additiva e assolutamente continua, esiste una funzione integrabile f tale che, per ogni E∈Σ, è

Una funzione assolutamente continua si annulla su insiemi di misura nulla. All'altro estremo troviamo la nozione di funzione che si annulla al di fuori di un insieme di misura nulla. Più precisamente, diremo che σ è singolare rispetto a μ se esiste un insieme E tale che μ(−E)=0 e σ(A)=0 per ogni A⊂E.

Teorema di decomposizione di Lebesgue: se (X, Σ, μ) è uno spazio di misura σ-finito e se σ è una funzione finita dappertutto e numerabilmente additiva su Σ, risulta

σ=σ₁+σ₂,

dove σ₁ è assolutamente continua e σ₂ è singolare.

Questa decomposizione di Lebesgue è unica, poiché, se

σ=σ₁+σ₂=σ1′+σ2′,

risulta

σ₁−σ1′=σ2′−σ₂,

e queste differenze sono allo stesso tempo assolutamente continue e singolari e pertanto si annullano identicamente.

Riassumendo, potremmo dire che l'integrale è una funzione di insieme numerabilmente additiva e che ogni funzione finita di insieme numerabilmente additiva differisce da un integrale per una funzione singolare.

e) Integrali muhipli.

Siano (X, Λ, α) e (Y, Ξ, β) due spazi di misura. Si può definire nel modo seguente una misura sul prodotto cartesiano X×Y. Sia Θ la classe di tutti gli insiemi della forma

A×B,

ove A∈Λ, B∈Ξ, α(A) è finito e β(B) è finito. Poniamo per definizione

τ(A×B)=α(A)β(B),

e utilizziamo questa funzione τ per costruire una misura esterna in X×Y mediante il procedimento che abbiamo descritto nel È a. Sia (X×Y, Σ, μ) lo spazio di misura che ne risulta. La misura μ prende il nome di misura prodotto definita da α e β.

Sia f una funzione su X×Y e, per ogni y∈Y, sia f( , y) la funzione definita su X generata da f, quando si tenga y costante. Se f( , y) è integrabile su uno spazio di misura (X, Λ, α), indichiamo l'integrale risultante mediante la

Supponiamo che f( , y) sia integrabile per quasi tutti gli y. La formula

definisce una funzione g q. o. su Y. Se questa funzione g è integrabile sullo spazio di misura (Y, Ξ, β), l'integrale multiplo di f è uguale per definizione a

L'altro integrale multiplo è definito, in modo analogo, mediante la

ove

Nei due teoremi principali sugli integrali multipli, si suppone che (X, Λ, α) e (Χ, Ξ, β) siano ambedue σ-finiti (cioè siano unioni di famiglie numerabili di insiemi di misura finita) e che μ sia la misura prodotto su X×Y. Il teorema di Fubini afferma che, se f è integrabile sullo spazio di misura (X×Y, Σ, μ), risulta

Il teorema di Tonelli fa dipendere l'integrabilità dall'esistenza di integrali multipli. Esso afferma che, se f è misurabile sullo spazio di misura (X×Y, Σ, μ) e se uno dei tre integrali

è finito, i tre integrali di f sono definiti e uguali fra loro.

I segni di valore assoluto nell'ultima ipotesi del teorema di Tonelli sono essenziali. Questo può sembrare strano, in quanto gli integrali di Lebesgue sono automaticamente convergenti in modo assoluto. Tuttavia gli integrali multipli non sono necessariamente assolutamente convergenti. Si tenga presente che la convergenza assoluta è garantita, in quanto l'integrabilità di f è espressa mediante l'integrabilità di f⁺ e f^-. Questo ragionamento, tuttavia, non è valido per gli integrali multipli a causa della differenza tra

Il controesempio tipico è dato dalla

In ciascun caso la prima integrazione può essere eseguita con i procedimenti usuali e questi calcoli mostrano che ambedue gli integrali sono convergenti, ma uno è positivo e l'altro è negativo.

3. Differenziazione.

Sia f integrabile secondo Lebesgue sulla retta reale e definiamo g ponendo

Sia σ la misura di Lebesgue-Stieltjes generata da g. Non è difficile far vedere che, per ogni insieme misurabile E,

Lo stesso si può fare per f^- e si vede così che ogni integrale di Lebesgue è la differenza di due misure di Lebesgue-Stieltjes.

Definita g come dianzi, il risultato a cui miriamo sarebbe g′=f⁺. Il rapporto incrementale che conduce a g′ è

ove μ è la misura di Lebesgue.

Lo studio della differenziazione degli integrali di Lebesgue può essere compiuto pertanto mediante le derivate delle misure di Lebesgue-Stieltjes rispetto alla misura di Lebesgue. Sia a una misura di Lebesgue-Stjeltjes e sia μ la misura di Lebesgue, ambedue sulla retta reale. La derivata σ′ è definita mediante la

ove I è un intervallo chiuso e I→x significa che x∈I e μ(I)→0.

In questo caso a una dimensione, la teoria si dimostra del tutto soddisfacente e i risultati principali sono i seguenti. Ogni misura finita di Lebesgue-Stieltjes è differenziabile q. o.; così ogni integrale di Lebesgue è differenziabile q. o. Inoltre, se σ=∫f, risulta σ′=f q. o. Infine, se σ è assolutamente continua, è σ=∫σ′.

Combinando quest'ultimo risultato con il teorema di decomposizione di Lebesgue, si giunge alla conclusione seguente. Sia σ una misura di Lebesgue-Stieltjes sulla retta reale e sia σ=σ₁+σ₂, ove σ₁ è assolutamente continua e σ₂ è singolare. Si ha σ2′=0 q. o. e quindi σ′=σ1′ q. o. D'altra parte σ₁=∫σ1′=∫σ′ cosicché

Questo equivale a dire che l'integrale di σ′ differisce per una funzione singolare da un'arbitraria antiderivata σ. Nella teoria di Lebesgue, dove la differenziabilità degli integrali può essere dimostrata soltanto quasi dappertutto, la costante di integrazione può essere sostituita da una funzione singolare non necessariamente costante.

La situazione diventa più complicata per dimensioni superiori. Sia σ la misura di Lebesgue-Stieltjes nel piano generata da g e sia I=(a, b]×(c, d]. Se μ è la misura di Lebesgue nel piano, risulta

Il limite iterato di questa espressione, quando anzitutto d→c e successivamente b→a, è

e questo è proprio il risultato che ci attendevamo. Gli integrali multipli sono calcolati prendendo le inverse di derivate parziali miste. Sfortunatamente non è disponibile questo tipo di procedimento di passaggio al limite per ottenere una teoria generale soddisfacente.

Sia {I_k} una successione di rettangoli chiusi sul piano. La successione {I_k} si chiama successione regolare convergente a x se: a) x∈I_k per ogni k; b) diam I_k→0; c) esiste una costante α>0 tale che, per ogni k, esiste un quadrato J_k⊃I_k, per cui risulta

ove μ è la misura di Lebesgue nel piano.

Grosso modo, una successione regolare è quella in cui non si permette ai rettangoli di diventare troppo ‛sottili'.

La derivata regolare di σ è definita ponendo

purché questo limite sia lo stesso per ogni successione regolare {I_k} convergente a x.

Lo strumento principale per arrivare ai teoremi di differenziabilità è un teorema di ricoprimento. Una classe Δ di rettangoli chiusi ricopre un insieme E del piano, nel senso di Vitali, se, per ogni x∈E, esiste una successione regolare {I_k} di rettangoli contenuti in Δ che converge a x.

Teorema di ricoprimento di Vitali: se Δ ricopre E nel senso di Vitali, esiste una successione disgiunta {I_n} di rettangoli appartenenti a Δ, tali che

Il teorema di Vitali non sussiste se cade la condizione di regolarità.

Per le derivate regolari nel piano, esiste una teoria del tutto analoga a quella del caso a una dimensione. Ogni misura finita di Lebesgue-Stieltjes è regolarmente differenziabile q. o. La derivata regolare di un integrale di Lebesgue è q. o. uguale all'integrando. Una misura assolutamente continua di Lebesgue-Stieltjes è uguale all'integrale della sua derivata regolare. Questi teoremi dipendono in modo essenziale dal teorema di ricoprimento di Vitali.

La derivata forte di σ è definita ponendo

purché questo limite sia lo stesso per ogni successione {I_k} (non necessariamente regolare) di rettangoli chiusi convergenti a x.

Quando il teorema di ricoprimento di Vitali non si può applicare, la teoria corrispondente è molto più limitata. L'unico teorema significativo è quello secondo cui, se f è limitata e integrabile secondo Lebesgue e se

per tutti gli E misurabili, risulta Dσ=f q.o.

In questo teorema la limitatezza di f è essenziale. Infatti, nello spazio L₁ delle funzioni integrabili secondo Lebesgue nel piano, l'insieme di quelle i cui integrali hanno una derivata forte e finita in ogni punto è un insieme della prima categoria, cioè una unione numerabile di insiemi rari. (Un insieme E in uno spazio topologico X si dice ‛raro' se la chiusura Ä di E non contiene alcun sottoinsieme aperto non vuoto di X). Poiché L₁ è completo (v. sotto, cap. 5) il teorema della categoria di Baire (secondo il quale nessuno spazio metrico completo è di prima categoria) mostra che ‛molti' integrali nel piano non sono fortemente differenziabili da nessuna parte. Si osservi che, se σ è la misura di Lebesgue-Stieltjes generata da g, per definire la derivata parziale mista di g occorre una derivata forte di σ.

La teoria bidimensionale si estende a n dimensioni senza cambiamenti essenziali. L'unico caso eccezionale è quello di dimensione 1, dove tutte le derivate sono regolari.

4. Integrazione negli spazi di Banach.

Sia (X, Σ, μ) uno spazio di misura e consideriamo funzioni su X non a valori reali, ma a valori in uno spazio di Banach B. Possiamo definire ancora funzioni semplici mediante la

ove gli E_i sono insiemi misurabili di misura finita e gli a_i sono ora elementi di B. Una funzione f da X a B si chiama misurabile se esiste una successione {ϕ_k} di funzioni semplici, tale che

per quasi tutti gli x.

L'integrale di una funzione semplice viene definito nel solito modo. Se

risulta

Il valore dell'integrale è, naturalmente, un elemento di B. Supponiamo che la funzione f da X a B sia misurabile e supponiamo che la funzione g, definita da g(x)=∥f(x)∥ per ogni x∈X, sia integrabile secondo Lebesgue. Si può in questo caso dimostrare che esiste uno e un solo a∈B tale che

per ogni successione {ϕ_k} di funzioni semplici, tali che ∥ϕ_k(x)∥≤g(x) per tutti i k e per quasi tutti gli x, e inoltre tali che

per quasi tutti gli x. L'elemento a si chiama integrale di Bochner di f su X e viene indicato con

Un integrale di Bochner su E si ottiene integrando fχ_E.

Se per ‛valore assoluto' di f(x) si intende ∥f(x)∥, l'integrabilità assoluta fa parte della definizione di integrale di Bochner. Si può dimostrare che l'integrale di Bochner è una funzione numerabilmente additiva e assolutamente continua da Σ a B.

Nel cap. 2, È c, abbiamo ricordato che vi possono essere più definizioni equivalenti di integrale di Lebesgue. Una di queste, quella data da Fréchet, è la seguente: sia X σ-finito e introduciamo una partizione P di X in un insieme numerabile {E_n} di insiemi disgiunti misurabili di misura finita. Una funzione a valori reali f è sommabile per P quando

è incondizionatamente convergente (cioè la convergenza della serie non dipende dall'ordine dei suoi termini) per ogni scelta di x_n∈E_n. Indicheremo con R(f, P) l'intervallo (eventualmente infinito) racchiuso dall'estremo superiore e dall'estremo inferiore di tutte queste somme. Se

consta di un solo numero a, f è integrabile e

Per funzioni f a valori reali, questo non è altro che l'integrale di Lebesgue. In particolare, l'integrabilità assoluta fa ancora parte della definizione.

G. Birkhoff generalizzò la definizione di Fréchet al caso di funzioni a valori in uno spazio di Banach; l'unica cosa che egli fu costretto a modificare fu la definizione di R(f, P), che Birkhoff assunse uguale all'inviluppo chiuso convesso di tutte le somme. L'integrale che ne risulta prende il nome di integrale di Birkhoff e viene indicato con

Se lo spazio di Banach B è il sistema dei numeri reali, gli integrali di Birkhoff e di Bochner coincidono con quello di Lebesgue. In generale tuttavia gli integrali di Birkhoff e di Bochner differiscono, perché la definizione di Birkhoff non implica l'integrabilità assoluta. La ragione sta nel concetto di sommabilità, il quale viene definito mediante la convergenza incondizionata delle serie; questa convergenza incondizionata implica la convergenza assoluta in uno spazio di Banach B se, e soltanto se, B ha dimensione finita.

L'integrale di Birkhoff è numerabilmente additivo e assolutamente continuo.

Pettis ha definito un integrale ricorrendo allo spazio duale B* di tutti i funzionali lineari continui su B. Data una funzione f da X a B e un F∈B*, consideriamo la funzione a valori reali F(f) su X. Diremo che f è integrabile secondo Pettis se, e soltanto se, esiste un unico a∈B tale che

per ogni F∈B*, ove l'integrale non è altro che l'integrale di Lebesgue. Scriveremo

Poiché negli integrali di Bochner e di Birkhoff compare la convergenza in norma, mentre nell'integrale di Pettis compare soltanto la convergenza debole, ci si potrebbe aspettare che l'integrale di Pettis sia più generale. Tuttavia, per le funzioni misurabili (secondo la definizione data all'inizio di questo capitolo), gli integrali di Birkhoff e di Pettis sono di fatto equivalenti.

Sia ora (X, Σ, μ) la retta reale con la misura di Lebesgue e consideriamo la teoria della differenziazione per questi integrali a valori in uno spazio di Banach. La differenziabilità in norma di σ nel punto x significa

mentre la differenziabilità debole di σ in x è espressa dalla

per ogni F∈B*. La differenziabilità in norma implica la differenziabilità debole, ma l'inverso sussiste soltanto per un numero limitato di spazi di Banach.

La prima difficoltà nasce dal fatto che, se B ha dimensione infinita, le funzioni assolutamente continue e numerabilmente additive da Σ a B non sono necessariamente differenziabili q. o., nemmeno in senso debole. Per questo motivo il teorema, nel quale intervengono effettivamente delle funzioni di insieme, deve necessariamente includere fra le ipotesi anche quella della differenziabilità.

Teorema: se σ è numerabilmente additiva, assolutamente continua e differenziabile in norma q. o., σ′ è integrabile secondo Bochner e

per ogni insieme misurabile E.

Il teorema inverso è più soddisfacente.

Teorema: se f è integrabile secondo Bochner e

per ogni insieme misurabile E, σ è differenziabile in norma q. o e risulta σ′=f q. o.

Vi sono delle funzioni integrabili secondo Birkhoff e secondo Pettis i cui integrali non sono differenziabili q. o. in senso debole.

5. Teoremi di convergenza.

Sia (X, Σ, μ) un qualsiasi spazio di misura. L'integrale di una funzione f misurabile e non negativa è l'estremo superiore degli integrali delle funzioni semplici dominate da f. Si dimostra facilmente che esiste una successione non decrescente {ϕ_n} di queste funzioni semplici, tale che

e

L'aspetto peculiare della teoria dell'integrazione di Lebesgue è che questo procedimento di passaggio al limite monotono può essere ripetuto.

Teorema della convergenza monotona di Lebesgue: sia f_n una successione non decrescente di funzioni non negative integrabili e sia

La funzione f è allora integrabile se, e soltanto se,

è finito; in tal caso risulta

Questo teorema è fondamentale nella teoria dell'integrazione di Lebesgue ed è interessante osservare come esso dipenda dalla teoria della misura. La misurabilità di f dipende dal fatto che questa funzione è un limite q. o. di funzioni misurabili e, come abbiamo notato nel cap. 2, È b, questo risultato dipende a sua volta dal fatto che Σ è una σ-algebra. Per definire l'integrale e dimostrare che esso è dato da un limite di integrali di funzioni semplici, basta far ricorso all'additività finita di μ. La dimostrazione del teorema della convergenza monotona di Lebesgue dipende tuttavia dal fatto che, per ogni successione di funzioni semplici convergenti in maniera monotona a f, gli integrali convergono all'integrale di f. Per dimostrare quest'ultimo enunciato occorre utilizzare i teoremi del limite per una successione crescente indicati per μ nel cap. 2 È a, per i quali μ deve essere numerabilmente additiva.

Per 1≤p〈∞, lo spazio L_p è per definizione lo spazio di tutte le funzioni misurabili tali che ∣f∣^p sia integrabile. Si vede facilmente che L_p è uno spazio lineare nel quale si può definire una norma ponendo

Di fatto questa è una pseudonorma, in quanto ∥f∥=0 implica soltanto che f=0 q. o.

Teorema di Riesz-Fischer: lo spazio lineare normato L_p è completo.

Questo è proprio il teorema che invano i matematici del XIX secolo si affannarono a ricercare. La ragione per cui nel XX secolo si riuscì a dimostrarlo sta nel fatto che la misurabilità delle funzioni si mantiene quando si passa ai limiti puntuali.

Dire che f_n→f₀ in L_p equivale a dire che

Questa si chiama convergenza in media p-esima e si esprime con

Quando p =1, di solito si sottintende p e la convergenza in media si scrive semplicemente

Nell'ultima parte di questo articolo ci occuperemo delle varie condizioni che conducono alla convergenza in media p-esima.

Un concetto utile, che apparve con la teoria della misura, è quello di convergenza in misura. Dire che

equivale a dire che, per ogni ε>0,

Si vede facilmente che la convergenza in media p-esima implica la convergenza in misura. L'affermazione inversa non sussiste, in quanto la convergenza in misura non impedisce agli integrali di tendere all'infinito. Esistono tuttavia numerosi teoremi interessanti, in cui si danno condizioni sulla grandezza degli integrali, le quali, con la convergenza in misura, implicano la convergenza in media p-esima.

Teorema della convergenza dominata di Lebesgue: sia g una funzione integrabile. Se

e se, per ogni n, ∣f_n∣^p≤g q. o., risulta

Questo è probabilmente il teorema meglio conosciuto e applicato più frequentemente. L'esempio seguente tuttavia mostra come esso non sia il miglior strumento possibile. Infatti, sia

si verifica facilmente con un calcolo diretto che f_n→0 in media; ma la funzione dominante minimale g è data da g(x)=x^-3/2 e questa non è integrabile su (0, 1].

Vale la pena di indicare sommariamente la linea dimostrativa del teorema della convergenza dominata di Lebesgue. Dato un ε>0, lo spazio X viene suddiviso in tre insiemi A_n, B_n e C dotati delle proprietà seguenti: X−C ha misura finita,

La prima disuguaglianza segue dal fatto che ∫ g è finito e numerabilmente additivo e pertanto gode di una proprietà nota come continuità in 0/ . Questo equivale a dire che, data una successione di insiemi, ciascuno dei quali contiene i successivi, tale che l'intersezione di tutti gli elementi della successione sia vuota, ∫ g tende a zero su questi insiemi. L'insieme C è semplicemente un insieme sufficientemente lontano da questa successione. Dalla convergenza in misura segue che, per n abbastanza grande, si può ottenere su A_n la terza disuguaglianza, mentre il rimanente insieme B_n può avere misura arbitrariamente piccola; la seconda disuguaglianza pertanto segue dalla continuità assoluta di ∫ g.

La continuità nell'insieme 0/ di ∫ g implica che le funzioni di insieme ∫ ∣f_n∣^p siano equicontinue in 0/ e la continuità assoluta di ∫ g fa sì che ∫ ∣f_n∣^p sia uniformemente assolutamente continua. Questo è il contributo totale della funzione dominante g nella dimostrazione che abbiamo or ora accennata e la convergenza in misura interviene soltanto nell'insieme X−C di misura finita; pertanto la stessa dimostrazione dà luogo al seguente risultato.

Teorema: se (1) le funzioni di insieme ∫ ∣f_n∣^p sono equicontinue su 0/ , (2) le funzioni d'insieme ∫ ∣f_n∣^p sono uniformemente assolutamente continue e (3) f_n→f₀ in misura su ciascun insieme di misura finita, risulta

La convergenza in media p-esima implica ciascuna delle tre ipotesi del teorema precedente; sicché questo è, in un certo senso, il miglior risultato possibile. Si può tuttavia dimostrare che l'ipotesi (1) implica la (2) e ciò dà luogo a un risultato più forte.

Teorema: se le funzioni d'insieme ∫ ∣f_n∣^p sono equi- continue su 0/ e se f_n→f₀ in misura su ciascun insieme di misura finita, risulta

Per p=1, si può giungere al teorema della convergenza in media per un'altra via, secondo la quale la convergenza debole in L₁ più la convergenza in misura implicano la convergenza in norma in L₁. La restrizione p=1 è fondamentale, anzitutto perché, per p>1, L_p è uno spazio di Banach riflessivo, mentre L₁ non è riflessivo.

Teorema: se f_n→f₀ in misura su ciascun insieme di misura finita e se, per ciascun E∈Σ,

risulta

È interessante osservare che la più semplice dimostrazione di questo teorema consiste nel ridurlo al teorema precedente mediante un risultato che Osgood dimostrò nel 1890. Secondo questo risultato di Osgood, una successione di funzioni continue, convergenti puntualmente su uno spazio metrico completo, deve essere equicontinua in qualche punto dello spazio.

Per applicare ora questo risultato, definiamo una misura finita ν su Σ ponendo

Si può dimostrare che Σ diventa uno spazio metrico completo rispetto alla distanza definita dalla ρ(A, B)=ν(A+−B)+ν(B−A). Le funzioni ∫ f_n sono continue su questo spazio e, per ipotesi, convergenti ‛puntualmente'. Pertanto esse sono equicontinue su qualche E∈Σ. Semplici considerazioni implicano allora che le funzioni ∫ ∣f_n∣ sono anch'esse equicontinue su E e, poiché esse sono additive, ne segue che esse sono equicontinue su 0/ . Il teorema dianzi enunciato può così essere ricondotto a quello che lo precede.

bibliografia

Birkhoff, G., Integration of functions with values in a Bonach space, in ‟Transactions of the American mathematical society", 1935, pp. 357-378.

Bochner, S., Integration von Funktionen, deren Werte die Elemente eines Vektorraumes sind, in ‟Fundamenta mathematicae", 1933, pp. 262-276.

Carathéodory, C., Vorlesungen über reelle Funktionen, Leipzig 1927².

Dunford, N., Schwartz, J., Linear operators, part I, General theory, New York 1958.

Fréchet, M., Sur l'intégrale d'une fonctionelle étendue à un ensemble abstrait, in ‟Bulletin de la Société mathématique de France", 1915, pp. 249-267.

Hahn, H., Rosenthal, A., Set functions, Albuquerque 1948.

Halmos, P. R., Measure theory, New York 1950.

Lebesgue, H., Leçons sur l'intégration, Paris 1928².

Munroe, M. E., Measure and integration, Reading 1971².

Pettis, B. J., On integration in vector spaces, in ‟Transactions of the American mathematical society", 1938, pp. 277-304.

Saks, S., Theory of the integral, Warszawa 1937.