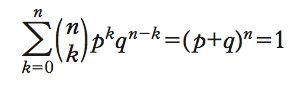binomiali, modelli

binomiali, modelli

Modelli di mercato dove sono negoziate attività il cui prezzo è funzione del tempo-stato descritto dal corrispondente nodo dell’albero binomiale (➔ anche albero, metodo ad). Ciò implica che in ogni nodo dell’albero si possono effettuare transazioni proprio a quei prezzi.

Alberi binomiali

In tali alberi da ogni nodo escono due soli rami: ci si può attendere che un ramo esca verso l’alto, in corrispondenza all’uscita di testa con probabilità p nel lancio di una moneta, e l’altro verso il basso (con probabilità q=1−p) al verificarsi di croce. Indipendentemente dalle probabilità, in un albero b. al tempo n troveremmo ben 2ⁿ nodi in corrispondenza alle 2ⁿ possibili sequenze di teste e croci che possono verificarsi nei primi n lanci. Un’utile semplificazione è che esso sia ricombinante, ovvero che al tempo n tutti i cammini con lo stesso numero k di teste (passi verso l’alto) sfocino nello stesso nodo (n,k). Negli alberi b. ricombinanti vi sono esattamente n+1 nodi al tempo n. Per quanto detto sopra, l’esistenza di un mercato come quello ipotizzato implica che in ogni nodo dell’albero gli operatori possano assumere posizioni lunghe o corte, effettuare cioè transazioni a pronti e a termine coerenti con la struttura dei prezzi delle attività negoziate. Precisamente, contratti a pronti il cui prezzo è quello corrente nel nodo e contratti a termine condizionati non solo al tempo ma anche allo stato futuro, il cui prezzo è quello del nodo corrispondente al tempo-stato futuro. In assenza di opportunità di arbitraggio, i prezzi a pronti e a termine delle attività negoziate devono obbedire a una particolare condizione: è necessario cioè che vi sia una struttura probabilistica, detta neutrale al rischio, secondo la quale i rendimenti periodali attesi (differenza tra prezzo futuro atteso e prezzo corrente diviso per il prezzo corrente) di tutte le attività negoziate sono vincolati a eguagliarsi e in particolare a eguagliare il rendimento periodale certo dell’attività non rischiosa. Conseguenza immediata di tale risultato è che in ogni combinazione tempo-stato il prezzo corrente di ogni attività negoziata è il valore attuale medio, condizionato all’informazione, dei prezzi dell’attività a una qualsiasi epoca futura. Sfruttando questa proprietà, particolari alberi b. ricombinanti sono usati, secondo un suggerimento dovuto a J.C. Cox, S.A. Ross e M.E. Rubinstein (Option pricing: a simplified approach, «Journal of Financial Economics», 1979, 7) per la valutazione approssimata dei prezzi di opzioni per cui non esistano formule chiuse nei corrispondenti modelli continui. La tipologia più nota di tali opzioni è quella delle opzioni put americane plain vanilla (➔ put option; opzioni vanilla) su un sottostante la cui evoluzione sia descritta da un modello b. moltiplicativo. L’albero permette, partendo dal valore a scadenza dell’opzione, di procedere all’indietro (backward) confrontando in ogni nodo il valore dell’opzione esercitata immediatamente con quello dell’opzione mantenuta viva. Quest’ultimo è pari al valore attuale medio secondo la probabilità neutrale al rischio dei due nodi raggiungibili a fine periodo.

Modello binomiale moltiplicativo

Descrive l’evoluzione del prezzo di un’attività finanziaria in funzione delle determinazioni assunte da un processo binomiale.  Precisamente, dato un prezzo iniziale A(0) e una coppia di coefficienti positivi (u,d) soddisfacente alla condizione u·d=1, il prezzo al tempo n nello stato k è A(n,k)= A(0)u^kdⁿ−k.

Coefficiente binomiale

Fornisce il numero delle combinazioni semplici di n elementi di classe k, ovvero il numero dei modi diversi in cui si possono ottenere k teste su n lanci consecutivi di una moneta. Per es., i primi k oppure gli ultimi k, o altre modalità meno compatte. Formalmente: C(n,k)=n! / k!·(n−k)! in cui compaiono vari fattoriali il cui significato generale è descritto dalla s!=s∙(s−1)∙(s−2)∙...∙2∙1, prodotto dei primi s numeri interi.

Binomio di Newton

Formula che per ogni data coppia (p,q=1−p) scompone (p+q)ⁿ al modo seguente:

Distribuzione binomiale

Distribuzione di probabilità della variabile aleatoria discreta somma di n variabili di Bernoulli, equidistribuite e indipendenti. Si può interpretare come il numero k di teste ottenute lanciando n volte una moneta avente probabilità p di uscita di testa in condizioni di indipendenza. Tale probabilità è uguale a:

P

(n,k)=p^k(1−p)^n−k·C(n,k).

Al variare di n, l’insieme delle distribuzioni b. si dice processo binomiale.

La distribuzione binomiale negativa è una generalizzazione, al caso di un numero reale r positivo qualunque, della distribuzione di Pascal, ovvero della distribuzione discreta di parametri p e n che descrive il numero di fallimenti (k) precedenti l’n-esimo successo in una sequenza di variabili di Bernoulli di parametro p.