Modelli matematici in immunologia
Modelli matematici in immunologia
La creazione di modelli del sistema immunitario nell'elaboratore può costituire un valido apporto alla ricerca immunologica. II modello può essere utilizzato sia come sostegno teorico nell'esplorazione e nello studio delle dinamiche dei processi immunologici, sia come strumento per lo sviluppo degli esperimenti in machina, cioè condotti mediante elaboratore. Nessun modello è in grado di riprodurre integralmente la realtà ma, attraverso il grado di simulazione ottenuto, è possibile giudicare la completezza dell'informazione immessa. In questo saggio, che non vuole essere una rassegna bensì una selezione soggettiva di argomenti, cercheremo di spiegare perché, quando e come viene utilizzato il modelling e quali sono i vantaggi che ne può trarre un ricercatore d'immunologia.
Dove si colloca il modelling?
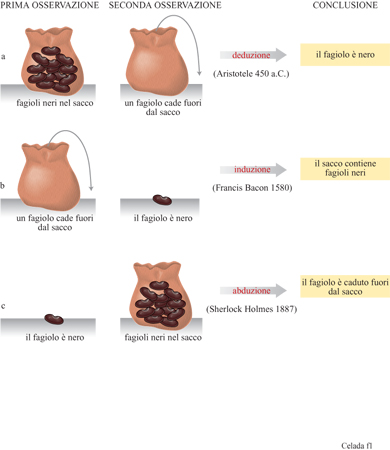
Secondo Charles Darwin, la selezione naturale si sviluppa su due binari opposti e complementari: l'ampliamento, attraverso la diversificazione, e la riduzione, attraverso la selezione. Potrebbe non essere del tutto casuale il fatto che anche il progresso scientifico si basi su due fasi opposte, la produzione di idee e la loro verifica. l lettori che si aggirano attorno ai sessant'anni di età ricorderanno di aver imparato al liceo che la rivoluzione metodo logica da cui è nata la scienza moderna è stata avviata da Francis Bacon e dagli empiristi inglesi ed è consistita nella sostituzione del pensiero deduttivo con quello induttivo. Ci si è in seguito resi conto che il ragionamento scientifico supera l'antinomia accademica deduzione-induzione dei maestri greci: C.S. Peirce ha dato una definizione al nuovo metodo, simile a quello usato dagli investigatori dei romanzi gialli, e lo ha chiamato abduzione (Eco e Seboek, 1983). La figura (fig. 1) illustra i tre tipi di ragionamento attraverso uno specchietto minimalista che potrebbe essere stato inventato da Umberto Eco se si fosse messo a osservare un sacchetto pieno di fagioli. Non vi è alcun dubbio che il metodo abduttivo, seguito da un test sperimentale, costituisca un pilastro centrale nel pensiero scientifico. K.R. Popper (1935), insistendo sulla necessità di falsificazione della teoria regnante, dipinge la ricerca come un'attività in cui la fase critica negativa prevale sull' acquisizione di nuovi fatti, nuove idee, nuove prospettive; un mondo in cui l'ipotesi, presentata con annessa indicazione dell' esperimento capace di confutarla, brilla frnché non viene sostituita da un'altra ipotesi con una indicazione simile. È vero che la confutazione può essere considerata come il riconoscimento e la correzione di un errore (Freeman e Skolimowsky, 1974) e che Peirce, piuttosto che Popper, valorizza l'immaginazione libera e creativa; tuttavia, il gioco della falsificazione non sembra rendere pienamente giustizia a quello che veramente avviene nella mente dei ricercatori, specialmente in quelle discipline che sono in continua espansione, come lo è stata l'immunologia negli ultimi decenni. Il grande numero di ricerche contemporaneamente in cantiere provoca una tumultuosa acquisizione di dati, spesso non coerenti, e la coesistenza di più ipotesi in conflitto tra loro complica la situazione. L'esigenza di un filtro matematico per la comprensione di tale complessità, ha motivato fin dall'inizio i nostri studi.
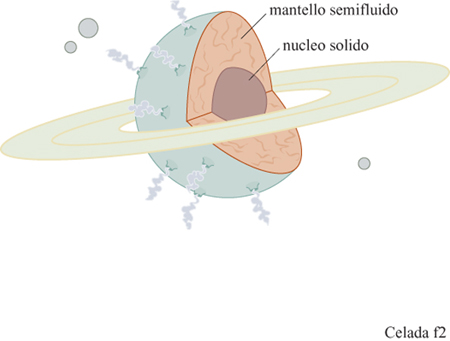
La descrizione del Pianeta Immunologia (fig. 2) fornita qualche anno fa da F. Celada (1992) evidenziava una struttura con un solido nucleo di certezze circondato da una grande area periferica di materiale fragile e semifragile, un anello come quello di Satumo, e alcuni problemi di navigazione. Non sapevamo a quel tempo che la stessa immagine era stata usata da rispettabili pensatori, con un significato più preciso. Secondo le idee di I. Lakatos (1974), un eminente filosofo della scienza, discepolo nonché critico di Popper, i ricercatori, lungi dall'intraprendere infiniti duelli rituali tra teorie e confutazioni "portano avanti un programma di ricerca, dotato di un nucleo solido e consensualmente riconosciuto, e hanno un'attitudine positiva nel definire i problemi, prevedere eventuali anomalie, elencarle a mano a mano che appaiono e superarle, a patto che il programma di ricerca regga il suo momentum". In altre parole, il nucleo dei fatti e delle ipotesi riesce a resistere agli assalti grazie a una cintura protettiva di nozioni ausiliarie che possono essere scartate o meno, sulla base delle evidenze sperimentali. Ma a volte i test sono difficili, o dispendiosi, o non proponibili per ragioni etiche o di opportunità politica e, in tal modo, ipotesi che sono incompatibili dal punto di vista logico coesistono per lunghi periodi di tempo. Questo rischia di rallentare il programma di ricerca fino a portarlo a una situazione di stallo, sicuramente fatale per un'impresa che è dinamica per definizione.
È in questo tipo di ambiente che una simulazione matematica può rappresentare una risorsa importante e uno strumento utile ai ricercatori. Infatti il modelling, da una parte crea le condizioni capaci di stimolare la germinazione di idee e ipotesi, dall'altra offre verifiche preliminari della loro fondatezza, agendo così su ambedue le fasi del processo scientifico.
Il modelling favorisce l'espansione del processo scientifico
Il modelling è reso possibile dal fatto che la realtà fisica e quella biologica sono defrnibili da quantità e relazioni numeriche. Il primo passo nella costruzione di qualsiasi modello consiste nel simulare da vicino un fenomeno fisico o biologico, usando termini puramente matematici. La scelta di questi termini, e delle loro relazioni, richiede l'impiego dell'immaginazione. Ovviamente, nessun modello riproduce integralmente la realtà ma, attraverso il grado di simulazione ottenuto, è possibile giudicare la completezza dell'informazione immessa. Generalmente, se questo grado è basso, il modello deve essere modificato nelle quantità iniziali o nei parametri o nelle variabili. Questa è propriamente l'attività creativa: fa parte della fase di espansione del processo scientifico, poiché l'introduzione di un parametro o di un fattore nel modello equivale all'adozione di un'ipotesi. Un altro modo in cui il modelling favorisce l'espansione si ha quando la simulazione funziona, cioè quando presenta un alto livello di corrispondenza con il fenomeno. A questo punto, la simulazione può fornire una ricostruzione della natura accessibile in tutte le sue parti, semplice da osservare e da valutare, con tutte le relazioni causali nettamente definite e le attrazioni dinamiche risolte. Questa è la base dell'uso dei modelli quali strumenti didattici, per esempio nell'insegnamento dell'immunologia (Celada e Seiden, 1992a). Peraltro, ancora più importante è la loro funzione come parte del vero motore del progresso scientifico, cioè la generazione di ipotesi e di abduzioni. Se la scienza si avvalesse esclusivamente del ragionamento induttivo, nessun modello avrebbe senso, in quanto non sarebbe in grado di sostituire l'osservazione empirica dei fenomeni naturali. Ma, dato che è l'abduzione la via della ricerca scientifica (v. figura 1c), un ruolo fondamentale è affidato all'immaginazione creativa e non c'è motivo perché lo stimolo per l'immaginazione non possa anche scoccare da una simulazione matematica. Anzi, questa potrà in certi casi essere ancora più stimolante del fenomeno naturale, che spesso è oscuro o criptico.
Pleiotropia, multicasualità e minimalismo
Le caratteristiche di alcune discipline scientifiche, compresi gli atteggiamenti dei loro cultori, possono essere influenzate dalla storia evolutiva dei sistemi che essi studiano. Per esempio, gli approcci distinti dei microbiologi e degli immunologi si possono ricondurre al fatto che i batteri sono apparsi 3 miliardi di anni fa, mentre i linfociti si sono evoluti 2700 milioni di anni dopo, per cui il sistema immunitario costituisce la più recente organizzazione cellulare e l'ultimo ramo evolutivo del regno animale. In immunologia, generalmente, molte possibili cause concorrenti o alternative vengono proposte come spiegazione di ogni fenomeno. La loro esistenza viene dimostrata in ambienti sperimentali costruiti in maniera appropriata e il relativo studio è subito pubblicato; ciò produce una ricchezza d'informazione che, a prima vista, può apparire contraddittoria e causare sconcerto. Tuttavia, va detto che una certa confusione è inevitabile, se si tiene conto di quanto rapidamente il 'giovane' sistema immunitario si sia evoluto, da meccanismo di stimolo-risposta aspecifico a sistema cognitivo sofisticato.
Come si verifica spesso in natura (Jacob, 1970), meccanismi nuovi si sono via via affiancati, ma non sostituiti, a quelli preesistenti. Perciò elementi molecolari e cellulari, apparentemente obsoleti, sono stati riutilizzati come supporto per le nuove risposte specifiche. Questo modo di procedere ha generato un gran numero di duplicazioni per ogni funzione, giustificate dal punto di vista evolutivo come polizze contro eventuali errori del sistema. Tuttavia, non vi sono dubbi che in vivo vi siano alcuni percorsi più favorevoli o principali, mentre la maggior parte delle soluzioni alternative rimane allo stato potenziale. D'altro canto, qualsiasi funzione normalmente inattiva può essere costretta a emergere in particolari situazioni. Poiché è il ricercatore che crea le condizioni di un esperimento, anche esasperando le, non è sorprendente che ogni singola soluzione possa essere ricreata e verificata. Questo procedimento è analiticamente corretto e sicuramente informativo; lo svantaggio è che si perde il senso della gerarchia delle possibilità e, purtroppo, anche la loro prospettiva biologica. Qui il modelling trova un'applicazione interessante, proprio perché può aiutare a rispondere agli interrogativi che nascono da questa situazione. Quanto è sufficiente per giustificare un dato percorso? Quali sono i meccanismi necessari? E quali vengono comunemente utilizzati? Il modelling, nei suoi vari aspetti, è uno strumento in grado di valutare le differenze, perché la sua vocazione è quella di semplificare, economizzare e minimalizzare. In una parola, l'opposto del modo di procedere della natura. Se il modello permette di fare esperimenti in machina, la discriminazione può essere raggiunta introducendo le molte funzioni possibili, una alla volta, nella simulazione: si comincia con la funzione l, poi si ripete la simulazione con le funzioni 2, 3, ... n; infine si paragonano i risultati, per valutare il loro grado di corrispondenza con l'osservazione, in modo da stabilire un ordine gerarchico tra l, 2, 3, ... n.
L'uso dei modelli come strumenti di verifica
La verifica più appropriata di un'ipotesi è l'esperimento; esso consiste nel riprodurre un fenomeno naturale in condizioni controllate e nel paragonare i risultati numerici con quelli attesi secondo la teoria ipotizzata. Controllare le condizioni di un esperimento significa essere in grado di variare tutti i parametri, uno alla volta, in modo da stabilire, attraverso strumenti adeguati, gli effetti di ognuno sui risultati. In immunologia, come in tutte le scienze biologiche, gli esperimenti sono diventati progressivamente più sofisticati e quindi più lontani dalle osservazioni in vivo. Le popolazioni cellulari, le cellule singole e i sistemi subcellulari vengono studiati in vitro, o attraverso sistemi intermedi quali le risposte adottive o gli animali transgenici. Un passo ulteriore in questa tendenza è lo svolgimento di esperimenti in machina, che utilizzano l'elaboratore per creare modelli dinamici del sistema e verificarli. Questo metodo di sperimentazione presenta una duttilità enorme, e il distacco dalla realtà è di poco maggiore rispetto a quello che si verifica negli esperimenti in vitro. Tuttavia, si tratta pur sempre di un terzo passo, e il grado di attinenza alla realtà fornito dal modelling è inversamente proporzionale al grado di astrazione inserito nella simulazione; per questo motivo gli esperimenti in machina non possono sostituire quelli in vivo o in vitro. Se i parametri introdotti sono realistici, però, i risultati della simulazione possono indicare quali direzioni saranno più favorevoli per la conduzione degli esperimenti sul campo. Questo è un valido contributo alla risoluzione dello strato grigio del Pianeta Immunologia e, in questo caso, gli esperimenti in machina possono determinare un risparmio di tempo, di denaro e di animali da laboratorio.
Dal momento che due ipotesi opposte possono, di fatto, coesistere per lunghi periodi di tempo prima che un esperimento decisivo possa essere programmato e svolto, il modelling è stato usato come strumento di discriminazione preliminare. Per questa utilizzazione, il modello deve essere sufficientemente neutrale per poter riprodurre, in maniera credibile, entrambi i postulati alternativi proposti. Lo scopo principale di questo esercizio è quello di rivelare i parametri critici sui quali poter focalizzare efficacemente gli esperimenti biologici. Un esempio di questo utilizzo è fornito dal modelling dell'ipermutazione della cellula B dopo la stimolazione antigenica primaria. Le osservazioni in vivo hanno trovato frequenze di mutazione molto maggiori sui segmenti genici che codificano i CDR (Complementarity Determining Regions), cioè i segmenti della regione variabile (V) dell'anticorpo che determinano la complementarità con l'antigene, rispetto alle regioni confinanti. Una teoria propone una distribuzione omogenea delle mutazioni su tutta la regione V e attribuisce la focalizzazione osservata alla selezione negativa che si esercita su mutanti colpiti da sostituzioni amminoacidiche in posizioni critiche, al di fuori dei segmenti CDR (Celada e Seiden, 1996). La teoria alternativa ipotizza, invece, che le mutazioni siano originariamente mirate sui segmenti CDR. È stato possibile simulare in un automa cellulare (v. oltre) entrambe le ipotesi e paragonare l'effetto dell'aumento della frequenza delle mutazioni nelle due condizioni, in termini di maturazione dell' affinità nella risposta. Per decidere quale delle due teorie sia giusta, basterà che i biologi sperimentali determinino due grandezze ancora imprecisate: la frequenza naturale di mutazione (numero di eventi per generazione per segmento genico) e la velocità di crescita dei cloni B. Il modello ha individuato in quest'ultima il parametro discriminante.
Metodi continui e discreti
l metodi di computazione usati per il modelling in immunologia si dividono in due grandi categorie, il modelling continuo e il modelling discreto, che non si escludono vicendevolmente. In teoria, entrambe le tecniche possono essere adoperate per tentare la soluzione di qualsiasi problema, nel senso che ambedue gli approcci rappresentano metodi universali. In pratica è importante fare molta attenzione nell'affrontare un dato problema immunologico in modo da scegliere l'approccio migliore. Ognuna delle due tecniche offre numerose varianti, ed è anche ipotizzabile per il futuro una sintesi dei due approcci. Per esempio, con l'aumentare della complessità dei modelli si può immaginare un automa di un sistema discreto in cui alcuni dei processi che avvengono nella cellula siano descritti da una serie di equazioni differenziali.
l metodi continui utilizzano equazioni differenziali per descrivere il sistema studiato. Un tipico esempio immunologico è la descrizione del comportamento nel tempo di popolazioni di cellule mediante equazioni contenenti termini che indicano, in maniera specifica, le grandezze che influenzano una popolazione cellulare, per esempio la nascita, la morte e la trasformazione delle cellule in altre forme, come cellule attivate e anergiche. Questo viene chiamato metodo continuo perché le variabili che descrivono le popolazioni sono espresse con numeri reali e non con i numeri interi che rappresentano, invece, le popolazioni di cellule nella realtà. Di solito questa generalizzazione non crea alcun problema, a meno che il numero delle cellule non sia talmente piccolo che anche la presenza o l'assenza di una singola unità sia determinante. Il vantaggio dei metodi continui è che non c'è alcun limite di misura, cosicché l'estrapolazione asintotica è facile. Un altro vantaggio molto importante è che le equazioni differenziali sono note e studiate da trecento anni e hanno una base matematica molto solida. Un ricercatore che utilizza un'equazione differenziale, generalmente ha un'idea approssimativa di come si comportino i vari termini e ricorre alla teoria matematica per ottenere soluzioni possibili per quell'equazione. Difficoltà nel loro utilizzo si presentano a coloro che dicono di affrontare i molti casi di non linearità che abbondano nei sistemi biologici. Spesso l'astrazione è molto maggiore di quanto avvenga per i metodi discreti, e le approssimazioni introdotte per risolvere le equazioni sono di natura matematica e possono non avere un significato biologico evidente.
Un metodo discreto che si è rivelato utile in immunologia è l'automa cellulare. Questa tecnica permette di descrivere, in uno spazio definito, le entità interagenti e le loro interazioni; queste si verificano ripetutamente durante una serie di unità di tempo, e quello che è successo in un'unità di tempo crea le premesse per il passo successivo. Uno dei punti di forza di questa tecnica è che le entità e i rapporti possono essere descritti in termini che sono molto simili alla situazione biologica. Inoltre, la non linearità non costituisce alcun problema. l casi complessi possono richiedere maggior tempo per la computazione ma, generalmente, non impediscono l'implementazione o la soluzione. D'altro canto però, la dimensione del sistema è generalmente piccola in confronto alla realtà, cosicché bisogna fare molta attenzione ai problemi derivanti dalla dimensione frnita, e l'estrapolazione asintotica è spesso difficile o impossibile. Infine, gli automi cellulari sono concetti relativamente nuovi in matematica; sono stati introdotti circa cinquanta anni fa e utilizzati seriamente solo a partire dagli anni Ottanta. Quindi, la loro base matematica è piuttosto debole e manca il supporto sia dell'esperienza sia della teoria.
In questo saggio presentiamo una descrizione dettagliata di entrambi i metodi. l lettori che desiderino approfondire l'argomento possono fare riferimento agli articoli di RR Mohler e collaboratori (1980), A.L. Perelson (1988), Perelson e G. Weisbuch (1992; 1997).
Modelli continui
La descrizione del sistema immunitario mediante equazioni differenziali si basa su una serie di tacite assunzioni. La quantità dei costituenti cellulari e molecolari, rispettivamente i linfociti e gli anticorpi, è rappresentata da grandi numeri. Quindi è giustificabile considerare la loro concentrazione nello spazio, cioè il loro numero per unità di volume, come una variabile continua. Inoltre, possiamo dimenticare la distribuzione dei costituenti nello spazio, assumendo una soluzione omogenea in cui le interazioni avvengono per collisioni casuali. Questo conduce a equazioni differenziali non lineari per i valori medi di concentrazione nello spazio dei costituenti, come è tipico per le teorie di campo medio in fisica statistica. Nella loro forma più semplice le equazioni sono simili a quelle che descrivono le dinamiche delle reazioni chimiche (legge dell'azione di massa) e alle equazioni di LotkaVolterra che descrivono i sistemi predatore-preda, cioè equazioni con interazioni bilineari. Il sistema di equazioni non lineari, che descrivono un network di interazioni, ha la seguente struttura:
ẋ(t) = guadagno - perdita
dove ẋ(t) indica la variazione delle concentrazioni x = {xi} nel tempo, che viene calcolata sulla differenza tra guadagno e perdita. Il guadagno, per esempio, dovuto alla secrezione di molecole da parte di una cellula dopo la stimolazione, o alla proliferazione cellulare, è descritto in termini semilineari o decisamente non lineari (v. oltre). Il guadagno dovuto alla generazione di nuove cellule da parte del midollo osseo e del timo è descritto da variabili nel tempo. La perdita, dovuta, per esempio, alla formazione di complessi (molecola-molecola, molecola-cellula) o alla fagocitosi è descritta anch' essa in termini semilineari o non lineari. Un tempo di vita definito conduce a termini lineari.
Quali informazioni si possono ottenere da sistemi dinamici non lineari? Lo stato del sistema è un punto nello spazio degli stati sviluppato dalle variabili Xi. La soluzione x(t) è rappresentata da una curva di stato. Una famiglia di curve rappresentanti soluzioni, partendo da condizioni iniziali diverse, descrive un flusso. Se guadagno = perdita, x è stazionario: x = Xo si chiama punto fisso. La stabilità dei punti fissi viene misurata osservando l'effetto di una piccola deviazione dal punto fisso: se aumenta nel tempo, il punto fisso è instabile; se diminuisce fino a raggiungere lo zero, il punto fisso è stabile, cioè è un attrattore. Possono esistere attrattori più complicati che descrivono un comportamento periodico, per esempio i cicli limite, o attrattori strani che descrivono un comportamento caotico. Nei casi sopraelencati il movimento è di tipo finito. Tuttavia, può succedere che il sistema perda la stabilità globale, e questo indicherà la necessità di una revisione del modello. Dopo aver cercato gli attrattori del flusso, si procede ad analizzare il comportamento globale in termini numerici. Un altro tipico argomento di studio è la risposta del sistema a perturbazioni dipendenti dal tempo quali, per esempio, la risposta immunitaria alle infezioni o alla terapia.
Vi sono diversi tipi di network importanti per il sistema immunitario: il network delle interazioni idiotipiche delle cellule B, i network delle interazioni di cellule T, la regolazione ormonale. Essi non sono indipendenti tra loro: per la proliferazione delle cellule B è necessaria l'assistenza delle cellule T. In principio, ogni network può essere collegato con qualsiasi altro; tuttavia, alcune delle interazioni sono forti e altre deboli, e questo offre la possibilità di defmire sotto sistemi. Si pensa che le proprietà dei sotto sisterni isolati cambino soltanto minimamente se si considerano interazioni con altri sottosistemi. Al contrario, è possibile l'insorgenza di proprietà olistiche che non si possono spiegare riducendo le a sotto sistemi o, in termini fisici, a fenomeni collettivi. L'architettura (o connettitura) del network è definita dalla forza dell'interazione tra i costituenti, che sono scelti a caso, a partire dal repertorio potenziale che è per ordine di grandezza più esteso. La descrizione dell'architettura casuale è oggetto di studio della fisica statistica. La forza delle interazioni che interessano le molecole e le cellule si chiama affinità e si pensa che sia in relazione con il grado di corrispondenza tra strutture spaziali complementari. Una descrizione matematica della congruità spaziale è tuttavia estremamente complessa, per non parlare della difficoltà di descrivere la traduzione della struttura primaria, la sequenza amminoacidica, in strutture secondarie la struttura chimica e, infine, in strutture terziarie e quatemarie la configurazione spaziale delle proteine. Un modello semplice utilizza stringhe binarie che possono interagire con stringhe complementari (v. oltre).
La forma più semplice dei termini che descrivono le interazioni è bilineare nelle concentrazioni degli elementi interattivi, e cioè proporzionale ad Xi Xj' come avviene per la cinetica delle reazioni chimiche nella legge dell'azione di massa. Questo metodo è certamente valido per descrivere le interazioni tra molecola e molecola ma viene utilizzato anche per descrivere dinamiche più complesse come quelle predatore-preda. Per creare un modello che incorpori proprietà cellulari specifiche, quali le soglie di attivazione, saturazione, supersaturazione o maturazione, sono necessari termini non lineari più complessi. Spesso si usano termini di formato xif(hi) dove f(h) è una curva a campana, data, per esempio, dall'espressione hn/(hn+ϑn), dove n rappresenta il coefficiente di Hill e hi è il campo che stimola Xi' Un campo di attive ricerche in corso è la derivazione di termini di interazione nelle variabili di campo medio, che possa descrivere sia le interazioni cellula-cellula sia quelle cellulamolecola partendo da principi primi.
La validità di equazioni di campo medio ha una limitazione principale: per piccole concentrazioni lo schema del campo medio non è più efficace perché diventano importanti le fluttuazioni. Per esempio, un ciclo limite può portare a valori molto piccoli di una variabile, che aumentano successivamente. Tuttavia, concentrazioni inferiori a una cellula per individuo non hanno alcun senso. In questi casi, generalmente si interviene manualmente per portare la concentrazione a zero. Però, in caso di basse concentrazioni il comportamento individuale di una cellula può rivelarsi determinante; e sarebbe perciò più appropriata una descrizione probabilistica. Di seguito elenchiamo alcune operazioni che permettono di creare modelli più vicini alla realtà.
Ritardo. - Esiste una gerarchia tra i livelli di descrizione: chimica intracellulare, cellule che interagiscono con cellule o con molecole, organi e organismi. Qui ci troviamo al secondo livello: le cellule vengono considerate come entità che reagiscono, se stimolate correttamente, con la proliferazione o la secrezione di molecole. Questo processo necessita di un certo lasso di tempo, un ritardo, che è tipicamente dello stesso ordine di altri tempi caratteristici del sistema. Il comportamento di sistemi ritardati, per esempio la stabilità di punti fissi, può risultare qualitativamente modificato.
Metadinamica. - L'architettura è generalmente non statica: vengono introdotti nuovi tipi di cellule provenienti dal midollo osseo, o dall'ipermutazione di cellule in proliferazione. Questo introduce una metadinamica stocastica.
Equazioni differenziali parziali. - Se rinunciamo all'assunto di omogeneità, permettiamo una distribuzione spaziale di concentrazioni che conducono alla diffusione; la descrizione appropriata è allora quella ottenuta attraverso equazioni differenziali parziali.
Modelli compartimentali. - Il midollo osseo, il timo, la milza, i linfonodi, sono organi separati nello spazio e altamente specializzati. Per descrivere queste caratteristiche sono stati creati modelli compartimentali.
Parametri distribuiti. - I parametri sono generalmente distribuiti e possono cambiare nel tempo, per esempio a causa dell'invecchiamento delle cellule o dell'organismo, o per commutazioni tra diverse modalità di funzionamento. Per affrontare sistemi altamente complessi e ricchi di fenomeni contrastanti, i primi passi devono essere rivolti alla creazione di modelli minimali. Infatti, se non comprendiamo prima i modelli più semplici, non potremo nemmeno capire quelli più sofisticati e realistici. Fortunatamente, la meccanica non lineare e la fisica statistica hanno sviluppato metodi adatti a descrivere fenomeni del tipo di quelli che si presentano tipicamente nel sistema immunitario. D'altra parte, impegnarsi nella descrizione di fenomeni immunitari è uno stimolo per arricchire ulteriormente questo armamentario metodologico. La necessità di assegnare valori realistici ai vari parametri che si presentano in queste simulazioni (affrnità, vite medie, tempi di ritardo) è una grossa sfida per i ricercatori sperimentali. Nei paragrafi seguenti presentiamo una selezione necessariamente soggettiva di argomenti, con lo scopo di fornire un'idea della gamma dei problemi e del tipo di domande che possono essere formulate e delle semplificazioni necessarie per la creazione di modelli mediante le equazioni differenziali.
Selezione clonale
In una serie di studi, G.I. BelI (1970; 1971a; 1971b) ha sviluppato un modello matematico minimo della selezione clonale e della produzione di anticorpi. Secondo la teoria della selezione clonale (Bumett, 1959), le cellule antigenespecifiche vengono selezionate dal contatto con l'antigene per la proliferazione e la produzione di anticorpi. Il modello descrive quattro tipi di cellule: cellule bersaglio, cioè piccoli linfociti che, quando vengono stimolati sufficientemente dall' antigene, si trasformano in cellule proliferanti, si moltiplicano e producono anticorpi. Con la diminuzione dello stimolo provocato dall'antigene, queste cellule si differenziano in plasmacellule, che sono produttrici terminali di anticorpi e cellule della memoria, che si pensa siano simili alle cellule bersaglio, le quali non producono anticorpi, possono essere stimolate e vivono a lungo. Le cellule bersaglio vengono stimolate se una frazione di recettori sufficientemente grande (assumendo che si sia raggiunto l'equilibrio) viene legata dagli antigeni. Il livello degli antigeni liberi seleziona alcuni gruppi di cellule a seconda della loro affinità per un dato antigene. Questo modello prevede un meccanismo per la tolleranza ad alte dosi: le cellule che vengono eccessivamente stimolate saranno distrutte.
La risposta del sistema verso l'antigene, calcolata numericamente, mostra un comportamento ragionevole. Nella fase iniziale vi è un aumento esponenziale di anticorpi. Per una stessa quantità di antigeni il sistema risponde in maniera più marcata a un'esposizione prolungata che non a una momentanea. La risposta secondaria è molto più rapida di quella primaria a causa del maggior numero di cellule della memoria che, grazie a una proliferazione selettiva, sono anche dotate di una maggiore affinità. Il modello offre anche una possibile spiegazione per la tolleranza a basso dosaggio: in caso di piccole dosi di antigene la stimolazione produce poche o nessuna cellula della memoria, cosicché il compartimento delle cellule bersaglio e delle cellule della memoria si svuota. L'inclusione di antigeni multivalenti apre la possibilità di descrivere la formazione di vaste aggregazioni di antigeni e di anticorpi nel fenomeno classico della precipitazione.
Ulteriori modifiche del modello originale, che non discuteremo in questa sede, possono essere introdotte per ottenere una migliore concordanza quantitativa con l'esperimento.
Interazioni idiotipo-antidiotipo e l'immagine interna dell'antigene
Sono stati immaginati vari meccanismi per spiegare la memoria immunologica (Vitetta et al., 1991): cellule B della memoria a vita lunga, come ipotizzato nel paragrafo precedente, cellule B stimolate da cellule follicolari dendritiche che presentano frammenti di antigene, cellule B della memoria idiotipiche stimolate dall'immagine interna dell'antigene fornita da cellule B antidiotipiche. Probabilmente tutti questi meccanismi esistono. È stato assodato il mantenimento delle cellule B della memoria per un periodo di tempo molto lungo. Tuttavia, è difficile distinguere, mediante esperimenti in vivo, se le cellule B della memoria vivano a lungo individualmente o se sopravvivano come popolazione. Questo è un caso particolarmente adatto per il modelling.
Nel quadro di un modello che descrive il network idiotipico di interazioni tra le cellule B, è stato studiato il sotto sistema di una coppia di cloni di cellule B idiotipici-antidiotipici, in presenza di antigene (Behn et al., 1993). È stato appurato che uno stato di popolazione non zero di entrambi i cloni è stabile solamente in presenza di cellule della memoria, suggerendo così una possibile sinergia di meccanismi diversi: cicli idiotipici -antidiotipici verrebbero stabilizzati dalle cellule della memoria che, a loro volta, potrebbero essere stimolate dalla loro controparte antidiotipica.
Le equazioni sono:
ẋ1 = -γx1 + (1 - k)mx2x1 + d1mx2 + (d1 + x1)m̄y
ẋ2 = -γx2 + (1 - k)mx1x2 + d2mx1
ẏ = αy - m̄x1y.
Qui x1 e x2 indicano le concentrazioni di anticorpi di idiotipo 1 e 2 indipendentemente dal fatto che siano liberi o funzionino come recettori sulla superficie cellulare, y denota la concentrazione di antigeni che si moltiplicano con la velocità α (virulenza) e ha affinità m̄ per l'idiotipo 1. L'affinità tra gli anticorpi idiotipici e antidiotipici è indicata con m, mentre γ è l'inverso della vita media dell'anticorpo. Le cellule della memoria sono rappresentate da di e ci si aspetta che siano presenti dopo una stimolazione sufficientemente forte dell'idiotipo corrispondente; il loro numero è zero allo stato vergine. l termini bilineari descrivono il guadagno dovuto alla stimolazione da parte degli antigeni o anticorpi antidiotipici e la perdita dovuta, rispettivamente, alla repressione o alla formazione dei complessi. Il parametro K permette di introdurre un'asimmetria tra stimolazione e inibizione. Qui abbiamo scelto K > 1, ossia il network è totalmente inibitorio come ipotizzato da N.K. Jerne (1974).
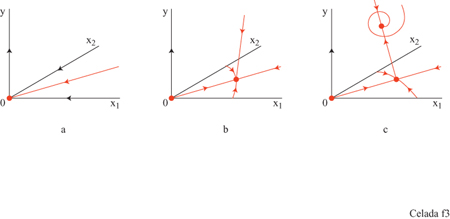
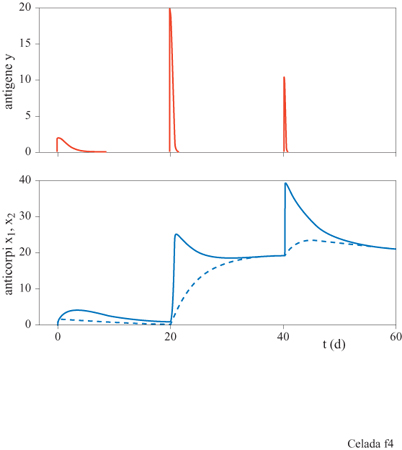
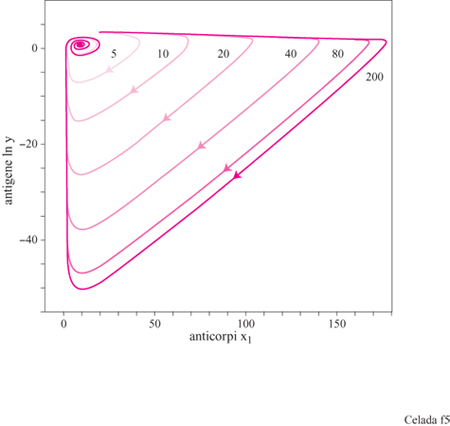
Il sistema ha, a seconda dell'assetto dei parametri, tre configurazioni di punti fissi che descrivono rispettivamente uno stato vergine, uno stato di immunità, e uno di infezione cronica (fig. 3). Il comportamento dinamico mostra una risposta secondaria che è più veloce e più forte di quella primaria (fig. 4). Nello stato di infezione cronica, un'esposizione ripetuta a piccole dosi di antigeni potrebbe allontanare il sistema dal punto fisso dell'infezione cronica e portarlo a uno stato caratterizzato da una maggiore concentrazione di anticorpi idiotipici. Quando la nuova esposizione all'antigene termina, il maggiore numero di anticorpi può essere sufficiente per curare l'infezione cronica (fig. 5). Questa strategia assomiglia a una terapia utilizzata all'inizio del secolo per mezzo della quale si cercava di curare la tubercolosi cronica provocandone l'acutizzazione.
Sistema immunitario centrale e controllo di doni autoreattivi
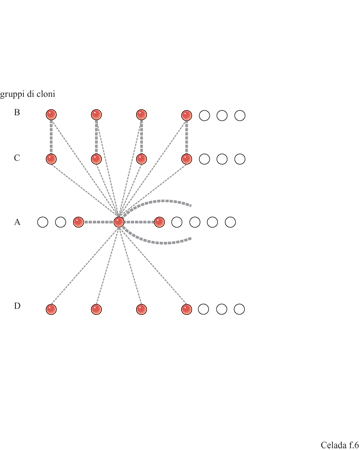
Come suggerisce A. Coutinho (1989), è vantaggioso fare una distinzione tra il sistema immunitario centrale, un network altamente integrato di relazioni complesse, e il sistema immunitario periferico costituito da cloni scollegati che forniscono la risposta agli antigeni esterni. Negli individui normali sani si trovano anticorpi autoreattivi, nonostante la selezione negativa dei linfociti T nel timo che abolisce l'autoreattività mediata dalle cellule T e dalle cellule B T -dipendenti. Il sistema immunitario centrale ha una dinamica interna non necessariamente determinata dagli antigeni e può giocare un ruolo nel controllo dei cloni autoreattivi come proposto da Jerne (1974) e da Coutinho (1989). Per descrivere tutto questo con un modello matematico, è stata studiata una dinamica non lineare dei componenti del sistema immunitario centrale basata su un'architettura semplificata (Sulzer et al., 1994). Idealizzando l'architettura di un network proposta da J. Stewart e F.I Varela (1989), vengono ipotizzati quattro cloni, A, B, C, D, distinti per la loro connettitura (fig. 6). I costituenti di A, cioè il nucleo del network, presentano una totale interazione con A, B, C e D; B è il gruppo speculare di C; D interagisce solo con A. Interazioni all'interno di A e tra B e C sono forti, le altre sono deboli. Le equazioni dinamiche sono:
Ẋ = -γxX1 + fp(hi)Xi - fd(hi)Xi
ẋi = -γxXi + pxfd(hi)Xi - bAhixi.
Dove X e xi indicano le concentrazioni di cellule B e anticorpi del clone i, rispettivamente; Yx e Yx sono gli inversi delle loro emivite. Il numero di cellule B aumenta grazie alla proliferazione, fp(hi)Xi e diminuisce per differenziazione terminale,fd(hi)Xi. Sia la proliferazione che la differenziazione sono governate da funzioni di saturazione fp/d(h) = Kp/dh/(h+ϑp/d) dove le velocità Kp/d e le soglie ϑp/d vengono scelte in modo appropriato, cosicché f(h) = fp(h) - fd(h) è un curva a campana. Il clone i è stimolato dal campo hi = ∑jN mijxj dove le affinità mij sono considerate uniformemente come l o η << l e producono rispettivamente un legame forte o debole.
Prima descriveremo le proprietà stazionarie del modello in assenza di un autoantigene. Una coppia idiotipo-antidiotipo isolata, cioè un membro dei gruppi speculari B e C, ha tre stati stabili. Oltre allo stato vergine, nel quale tutte le concentrazioni sono a zero, vi sono due stati di memoria in cui la popolazione di un clone è alta, mentre quella dell'altro è bassa.
Se includiamo l'interazione con A, le coppie idiotipo-antidiotipo mantengono qualitativamente le loro proprietà. Esse forniscono una stimolazione dei cloni centrali A che porta, in dipendenza sia della forza dell' accoppiamento η che delle condizioni iniziali, a quattro situazioni qualitativamente diverse che si escludono a vicenda. Nella soluzione coppia indipendente ciascuna coppia B-C raggiunge uno dei suoi tre stati possibili e fornisce uno stimolo ad A che è troppo basso o troppo alto per causare espansione cosicché A muore. Nella soluzione coppia appaiata, il centro A e le coppie B-C coesistono e contribuiscono a mantenere l'equilibrio. Nella soluzione singolo appaiato i membri dei cloni B o C possono essere in equilibrio con A e, al tempo stesso, iperstimolare il proprio partner antidiotipico: solamente in questo caso i cloni D possono coesistere con i cloni B o C. Infine, i cloni A possono mantenere il loro equilibrio autonomamente formando un centro polireattivo.
Questo schema non cambia qualitativamente quando alcuni cloni riconoscono l' autoantigene Ui che si assume avere una concentrazione costante. Il legame dell'autoantigene, cioè l'antigene self, con i amplifica il campo a
hi = ∑jN mijxj + ui. Dal momento che la popolazione di A è sempre bassa o a zero, il legame dell'autoantigene a un membro di A non causa alcuna autoimmunità. Lo stesso avviene se l'autoantigene si lega con un clone dei gruppi speculari B o C con bassa popolazione: in questo caso, la coppia corrispondente è in uno stato di tolleranza. I cloni autoreagenti sono controllati dai loro antidiotipi. Se, tuttavia, l'autoantigene si lega a un clone dei gruppi speculari con un alto tasso di popolazione, la coppia corrispondente è in uno stato di auto immunità. Un'alta concentrazione di autoanticorpi può causare reazioni autoimmuni. Se invece cadono sia la concentrazione di autoanticorpi sia quella dei loro antianticorpi, la coppia è in uno stato neutro: il sistema non è auto immune allo stato attuale ma è anche non protetto contro l' autoimmunità.
L'analisi numerica della risposta dinamica contro gli antigeni esterni rivela che il sistema può essere spostato dal suo stato di tolleranza, in dipendenza della concentrazione degli autoantigeni e della dose iniziale di antigeni esterni, oltre che della velocità di rimozione dei complessi. È stato osservato che l'induzione all'autoimmunità è molto meno probabile se l' antigene esterno è riconosciuto dagli autoanticorpi di quanto lo sia se è riconosciuto dai loro antianticorpi. D'altra parte, l'incontro con un antigene esterno può anche indurre la transizione da uno stato di autoimmunità a quello precedente di tolleranza. In questo caso, un antigene esterno che si lega agli antianticorpi, imitando così l'autoantigene, è estremamente efficace nel provocare una cura spontanea. La semplificazione più importante nel contesto sopra descritto è stata quella di omettere i linfociti T quali componenti espliciti del network Questo equivale ad assumere che le cellule B del network ottengono sempre aiuto sufficiente dalle cellule T. Essendo il nostro scopo quello di studiare la soppressione idiotipica quale meccanismo per controllare le cellule B autore agenti, questa semplificazione ci è parsa giustificata. Al contrario, il problema che ci apprestiamo a considerare necessita di un'analisi dettagliata ed esplicita del network che fornisce la regolazione da cellule T.
Terapia desensibilizzante nelle patologie allergiche
La desensibilizzazione è una terapia efficace nella cura delle malattie allergiche di tipo I: le reazioni di tipo I sono quelle provocate, secondo la classificazione di P.G.R. GelI e R.R.A. Coombs, dagli anticorpi IgE, come si verifica in alcuni casi di orticaria o di asma allergico. Vi sono molti dati empirici sulla desensibilizzazione, ma questa terapia è al momento priva di una chiara base teorica. La regolazione da cellule T sembra essere un fattore cruciale nelle manifestazioni allergiche. Il modello matematico qui discusso (Behn et al., 1998) spiega la desensibilizzazione come fenomeno dinamico della regolazione T.
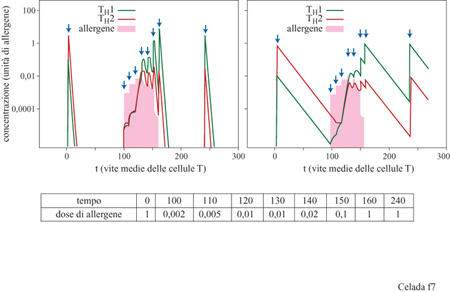
Vi sono due sottocategorie di cellule T helper, THl e TH2, che differiscono nel tipo di cito chine secrete e per le reazioni immunitarie che favoriscono (Powrie e Coffmann, 1993; Mosmann e Sad, 1996). Mediante le loro citochine, le cellule T H2 stimolano la produzione di anticorpi, in particolare gli anticorpi IgE, che caratterizzano l'allergia di tipo I. Il sotto sistema THl induce un'ipersensibilità di tipo ritardato e, entro certi limiti, la produzione di altri tipi di anticorpi oltre alle IgE. Le cito chine secrete dalle cellule T helper hanno effetti auto crini e soppressivi incrociati. Quindi c'è sempre un sotto sistema di cellule T che risulta dominante. Certamente può esserci più di un motivo per cui un antigene causa una risposta immunitaria THl e un altro una TH2. La presenza di citochine, il tipo di cellule che presentano l'antigene, la natura e la concentrazione dell'antigene stesso e, probabilmente, fattori genetici possono avere un ruolo significativo. L'allergia di tipo I è una tipica risposta TH2: la dose di allergeni è uno dei regolatori più importanti della scelta tra TH1 e TH2. Per concentrazione antigeniche medie e alte, la risposta immunitaria è piuttosto dominata dalle cellule TH2, mentre la bassa concentrazione dell' antigene porta a una risposta immunitaria dominata da quelle TH1 (Romagnani, 1995; Mosmann e Sad, 1996). La terapia di desensibilizzazione, con iniezione di allergeni in quantità crescenti, inizia con bassi livelli di allergeni che, quindi, provocano una risposta dominata da TH1. Attraverso la soppressione incrociata TH1- H2, si instaura una dominanza iniziale di TH1 che può persistere anche quando si raggiungono livelli alti di allergeni. Le nostre ipotesi portano ad affermare che la desensibilizzazione determina una risposta immunitaria dominata da TH1. Dopo la terapia il numero di cellule allergene-specifiche TH2 diminuisce a causa della dominanza del sotto sistema TH1; una quantità minore di cellule TH2 risulta in una minore produzione di IgE, e perciò in un'attenuazione della sintomatologia allergica. Questo meccanismo è alla base di un modello matematico che consiste in sei equazioni differenziali non lineari che descrivono la dinamica delle concentrazioni delle cellule T vergini, delle cellule T H l e TH2, delle cellule della memoria corrispondenti, e dell'allergene (Behn et al., 1998). Il contatto con l'allergene porta alla produzione sia di cellule T specifiche, sia di cellule T della memoria da parte delle cellule T vergini. Sono previsti gli effetti autocrini e soppressivi incrociati mediati dalle cito chine la cui concentrazione è considerata proporzionale al numero di cellule T responsabili di questo tipo di segnale extracellulare. Le citochine che provengono da altre cellule e da altri processi immunitari sono considerate come background. L'eliminazione degli allergeni è proporzionale al prodotto di cellule T e allergene; le cellule della memoria sono considerate cellule longeve (Bradley et al., 1993), che non sono ristimolate continuamente. I parametri vengono scelti in modo che inizialmente, prima della terapia, dosi basse (o alte) di allergeni causino una risposta dominata da cellule THl (o TH2). Curiosamente, si scopre una sorta di crinale nello spazio degli stati, che separa le risposte immunitarie dominate dalle cellule THl da quelle dominate dalle cellule TH2. Perché la terapia sia efficace è necessario attraversare questo crinale. Ciò porta, temporaneamente, a uno stato caratterizzato da una risposta immunitaria dominata dalle cellule T H l anche a una dose alta di allergene, da interpretarsi come stato desensibilizzato (fig. 7). Per mantenere questo stato la terapia dovrebbe essere ripetuta a intervalli regolari e questo vale sia in vivo che nel modello.
Il modello è robusto rispetto a variazioni dei parametri entro certi limiti e può riprodurre in maniera sorprendente le caratteristiche qualitative terapeutiche che producono o meno l'effetto desiderato. Le stimolazioni eseguite nel modello, per esempio, dimostrano che anche una sola mancata iniezione di allergene durante la terapia, o la somministrazione di una dose troppo alta dello stesso può mettere a rischio la riuscita della desensibilizzazione. Nel caso di una mancata iniezione di allergeni può essere di aiuto aumentare la dose successiva. La regolazione THI-TH2, specialmente il passaggio dalla dominanza di un sottosistema di cellule T all'altro, riveste un ruolo cruciale non solamente nelle allergie: profili alterati nella produzione di cito chine di tipo THl o TH2 sono anche associati, nell'uomo, ad altre patologie come candido si, AIDS, leishmaniosi e malattie autoimmuni.
Modelli discreti
Il vantaggio delle dinamiche discrete risiede nel fatto che la natura matematica dei processi, che vengono inseriti nel modello, non ha un'eccessiva influenza sull'implementazione del modello stesso. Per esempio, in primo luogo, la non linearità non causerà nessuna difficoltà reale nella simulazione. In secondo luogo, casi speciali possono essere previsti senza problemi. Infine, e forse questo rappresenta l'elemento più importante, la struttura della simulazione può avere una corrispondenza molto stretta con i processi immunologici che vengono modellati. Infatti, i parametri e le entità possono essere descritte in termini biologici e le approssimazioni fatte nel costruire il modello sono generalmente di carattere biologico più che matematico. Questo tipo di vantaggio ha un suo prezzo: in primo luogo le simulazioni saranno di dimensioni molto inferiori rispetto a quelle create con le equazioni differenziali; sarà perciò più difficile estrapolare valori dove gli effetti della grandezza frnita non si facciano più sentire. Questo tipo di problema riveste una particolare importanza in fisica, mentre i sistemi biologici reali, come quelli immunologici, sono spesso alquanto finiti dal punto di vista matematico. Un altro svantaggio è che un sistema discreto può consumare, in un elaboratore, più tempo e memoria rispetto a un sistema di equazioni differenziali, anche se non è sempre cosÌ. Il progresso tecnico degli elaboratori negli ultimi tempi ha comunque alleviato decisamente questo tipo di problema.
Automi binari
I sistemi dinamici discreti hanno una grande varietà di dimensioni e di complessità. Come abbiamo accennato, uno dei vantaggi dei sistemi discreti è la capacità di affrontare la complessità in modo semplice e diretto. Perciò, anche sistemi discreti molto semplici possono essere di grande utilità: inizieremo la nostra discussione proprio con un'implementazione molto semplice ma molto utile. Questo esempio utilizza un automa per seguire le dinamiche inerenti a un set di regole che descrive il comportamento generale di alcuni processi. Questa tecnica in immunologia è stata proposta per la prima volta da M. Kaufman, e collaboratori (1985). Il titolo stesso del lavoro è emblematico: Verso un 'analisi logica della risposta immunitaria. L'esempio preciso di cui ci occupiamo è stato pubblicato da D. Chowdhury e collaboratori (1990). Essi elencano un gruppo di semplici regole che determinano la risposta immunitaria a un antigene esterno. Il modello include l'antigene, le cellule B, le cellule T helper, le cellule suppressor e gli anticorpi. L'idea è che gli anticorpi eliminano gli antigeni, ma la produzione di anticorpi è un processo a fasi multiple. Il processo è descritto dalle regole seguenti:
Anticorpi Ab←Ag e B e TH
Soppressori Ts←Ts o TH
Helper Tw←[Ag e (non Ts)] o TH
Cellule B B←(Ag o B) e TH
Antigene Ag←Ag e (non Ab).
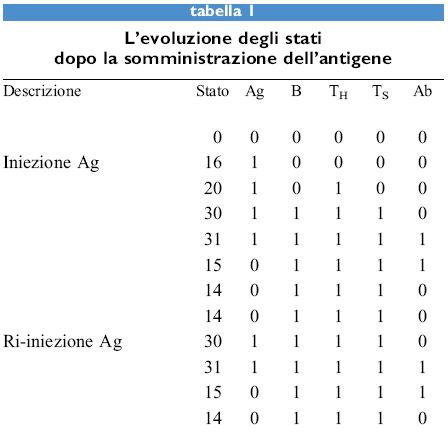
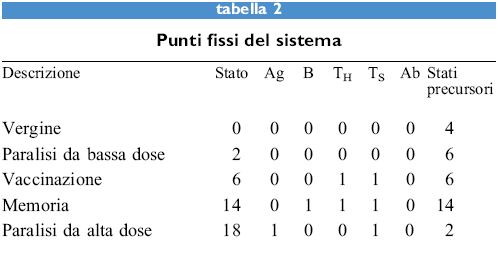
I valori dei cinque parametri sono binari, cioè l oppure O, e le regole sono regole logiche: e, o, non, sono operatori logici. Quindi la prima regola è da interpretarsi come segue: il valore di Ab sarà l solo se Ag, Ab e TH sono tutti l, altrimenti Ab è 0. Lo stato del sistema in qualsiasi momento può essere rappresentato dal numero binario a 5 cifre che rappresenta le 5 variabili e il suo valore è dato dall'equivalente decimale di tale numero. Per esempio, il numero binario 10.000 corrisponde allo stato 16. Questo sistema presenta 2⁵ = 32 stati possibili perché ognuno dei 5 parametri può essere 1 o 0. La tabella (tab. I) riporta la risposta di un sistema vergine all'antigene. La prima colonna mostra il numero dei 32 stati possibili che evolvono verso uno dei punti fissi. La maggior parte degli stati evolve verso lo stato della memoria (14) mentre lo stato di paralisi ad alta dose è alquanto raro, l'unico altro stato che evolve fino a esso è il 26 (Ag + B + Ts). Tuttavia, il 26 è uno stato definito giardino dell'Eden, nel senso che non c'è alcuno stato che lo raggiunga. Gli unici stati che appaiono in un percorso evolutivo, oltre ai punti fissi, sono 4, 15, 20, 30 e 31. Tutti questi ultimi evolvono verso 14, tranne il 4 che diventa 6. Quindi, i punti fissi 0, 2 e 18 vengono solo raggiunti partendo da stati giardino dell 'Eden. La prima riga della tabella l, stato 0, è il sistema vergine. L'aggiunta dell' antigene, portando Ag a 1, porta allo stato 16. Le regole sono quindi applicate a un dato stato per raggiungere lo stato seguente. Lo stato 14 è detto punto fisso poiché l'applicazione delle regole non lo modifica. Se l'antigene è iniettato di nuovo in questo stato, come è mostrato nella tabella l, si ritorna al medesimo punto fisso, ma in questo caso sono stati necessari solo tre passaggi invece dei cinque nel caso dell'iniezione primaria di antigene. Dei 32 stati possibili 5 sono punti fissi. Essi sono mostrati nella tabella (tab. 2), insieme con la dizione indicante lo stato corrispondente del sistema immunitario. Lo stato di vaccinazione è interessante per il fatto che raggiunge lo stato della memoria quattro passaggi dopo l'esposizione all'antigene.
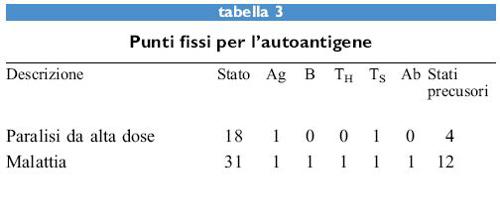
Ora vediamo cosa accade quando l' antigene è considerato come autoantigene ed è sempre presente, ossia, Ag è sempre 1. l punti fissi cambiano come è mostrato nella tabella (tab. 3). In questo caso ci sono solamente 16 stati possibili poiché Ag è sempre 1. Per affrontare il problema dell'autoantigene può essere aggiunta una cellula killer che eliminerà le cellule TH che rispondono all'autoantigene. La regola per questa cellula sarà:
Cellule T Killer K←(Ag e TH) e (non Ts);
modifichiamo la regola degli helper per tener conto dei killer, come segue:
Cellule T helper TH←(non K) e [Ag e (non Ts)] o TH.
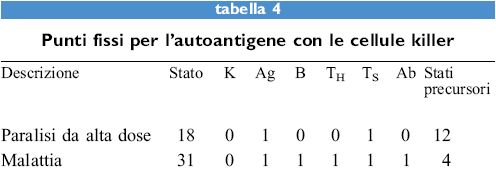
l risultati sono mostrati nella tabella (tab. 4). l punti fissi restano immutati, tuttavia ora solo 1/8 degli stati precursori porta alla malattia, mentre senza le cellule killer erano i 3/4. Inoltre vi sono 16 nuovi stati che hanno una popolazione di cellule killer e tutte queste raggiungono lo stato 18. Questi semplici modelli certamente non danno un quadro completo e dettagliato delle dinamiche del sistema, tuttavia forniscono un panorama dei possibili stati del sistema, la loro dominanza e un'indicazione di come possono essere affrontati. Questa tecnica è in grado di fornire un diagramma pragmatico di ciò che è possibile per un particolare processo. Si può anche aumentare la complessità del sistema a volontà: laddove i due stati di un parametro binario risultino insufficienti, si potranno prendere in considerazione tre o quattro stati. In questo caso il sistema diventa un po' più complesso ma la sua analisi mediante l'elaboratore rimane semplice e chiara.
Automi cellulari
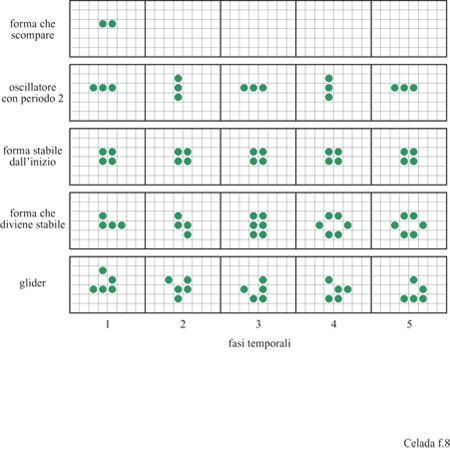
Possono esistere automi cellulari in diverse forme (Wolfram, 1986) ma l'esempio emblematico che discuteremo in questa sede può essere descritto come una scacchiera i cui siti possono essere sia vuoti che occupati da una pedina, cioè nuovamente un sistema binario. Lo stato di un sito può cambiare per l'influenza esercitata da quello dei siti adiacenti. Un esempio interessante di questa categoria di automi è il gioco della vita di J. Conway (Gardner, 1970). L'evoluzione procede grazie alle due regole seguenti: una casella occupata rimarrà occupata nell 'unità successiva di tempo se, e solamente se, vi sono due o tre caselle adiacenti occupate; una casella vuota diverrà occupata nell'unità di tempo successiva se, e solamente se, vi sono tre caselle adiacenti occupate. Caselle adiacenti sono considerati gli otto siti che circondano un sito su una scacchiera. È da notare che un automa cellulare è discreto sia nello spazio che nel tempo e tutte le azioni sono simultanee. In altre parole, le regole vengono applicate a tutti i siti contemporaneamente e, sulla base del risultato, tutti i siti vengono aggiornati simultaneamente, nella stessa unità di tempo (time step). Queste semplici regole producono, partendo da distribuzioni casuali di pedine sulla scacchiera, un numero sorprendentemente ricco di forme stabili interessanti, alcuni delle quali sono mostrate nella figura (fig. 8). Una forma particolarmente interessante è il glider (aliante), che consiste in un oscillatore stabile con periodo 5 e si muove in maniera caratteristica sulla scacchiera.
Un automa cellulare per il sistema immunitario umorale
lMMSlM (Seiden e Celada, 1992; Celada e Seiden, 1992b) rappresenta un tentativo di creare un modello della branca umorale del sistema immunitario e di analizzare problemi connessi con la selezione clonale. Esso è basato sul principio dell'automa cellulare, le cui regole formali sono le seguenti (Wolfram, 1984): consiste in un lattice discreto di siti; evolve in unità di tempo discrete; ogni sito può assumere un numero finito di stati; il valore di ciascun sito evolve secondo regole deterministiche; le regole per l'evoluzione di un sito sono basate esclusivamente sullo stato dei siti prossimali.
Il sistema usato per lMMSlM è stato definito un automa cellulare generalizzato o un automa ipercellulare, perché sono state introdotte alcune modifiche che riguardano parti della quarta e quinta regola sopra elencate. L'aggettivo deterministiche, attribuito alle regole, è stato cambiato in probabilistiche; la defrnizione di stato dei siti prossimali è stata sostiuita da stato del sito stesso.
Inoltre, è stata aggiunta una sesta regola: entità possono diffondere da un sito all'altro.
Il modello lMMSlM usa una griglia bidimensionale triangolare, che rappresenta una piccola porzione dell'organismo. In questo tipo di griglia ogni sito ne ha sei vicini identici, invece che otto di due cate gorie (quattro di lato e quattro di spigolo), nel caso di griglia quadrata.
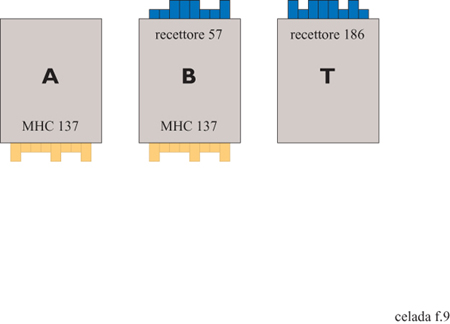
Ogni sito, invece di essere binario come nel gioco della vita, può essere popolato da un numero di entità distinte di diversi tipi. Le entità in questione sono: cellule B, cellule T, cellule che presentano l'antigene (APC, Antigen Presenting Cells), antigeni, anticorpi e complessi antigene-anticorpo. Queste entità posseggono recettori binari, epitopi e peptidi. Schemi dei tre tipi cellulari sono mostrate nella figura (fig. 9) per il caso dei recettori da 8 bit. La stringa rappresenta il recettore tipico del clone specifico che caratterizza le cellule B e T. Inoltre, le cellule B e APC posseggono molecole di istocompatibilità di classe II. Una cellula APC non è specifica, quindi non ha un recettore specifico ma avrà le stesse molecole MHC (Major Histocompatibility Complex, complesso maggiore di istocompatibilità) che possiedono la cellula B. Inoltre, una cellula APC possiede un recettore Fc. Quest'ultimo non è specificato sulla cellula poiché è lo stesso per tutte le cellule APC; tuttavia, è capace di legarsi alla regione Fc di un anticorpo quando questo è legato all'antigene.
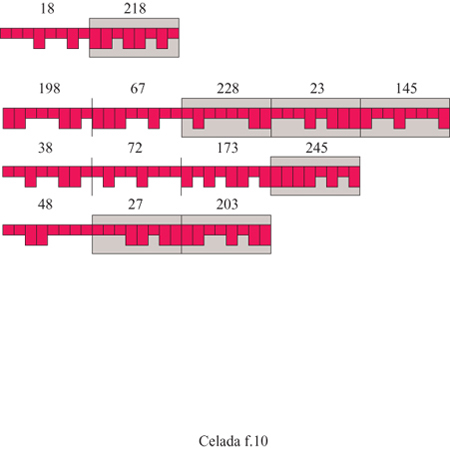
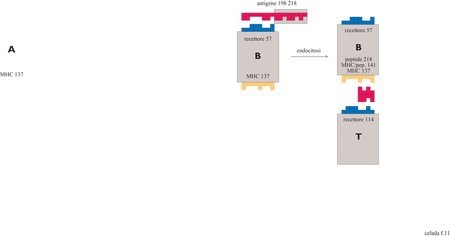
Gli antigeni sono rappresentati da vari segmenti, cioè epitopi e peptidi. Gli epitopi sono i segmenti ai quali le cellule A, cioè le APC, e B possono legarsi. Una cellula B può legarsi se il suo recettore coincide con l'antigene in modo complementare, ossia ogni bit 0 si lega a 1 e viceversa. Quando l'antigene è intemalizzato, i segmenti peptidici verranno presentati sulla molecola MHC; nella realtà, si ottengono con il processamento dell' antigene. Nel modello i peptidi devono essere specificati insieme agli epitopi quando si definisce l'antigene: esempi di antigeni sono mostrati in figura (fig. 10). In condizioni adeguate, come viene descritto di seguito, le cellule B producono anticorpi contenenti un paratopo, identico al recettore della cellula che lo produce, e un peptide. È anche presente un epitopo Fc che non ha bisogno di essere definito in maniera esplicita poiché è lo stesso per tutti gli anticorpi. Il centro del modello consiste nella simulazione della cooperazione cellulare: come l'antigene venga catturato e processato e come la sua cattura e il suo processamento influiscano sulle successive azioni delle cellule specifiche.
Nella figura (fig. 11) sono mostrate, in maniera schematica, la cattura e il processamento dell' antigene da parte delle cellule B che sono fornite di un recettore specifico per gli antigeni. Inizialmente una cellula B tenta di legarsi con gli epitopi dell'antigene; questo legame dipende dal numero di bit coincidenti presenti. La forza del legame è massima se c'è complementarità per tutti i bit, e diminuisce all' aumentare del numero di bit non complementari. Al di sotto di una certa soglia non si ha legame: ciò si verifica quando si ha l mismatch (non congruità) nel caso di stringhe da 8 bit e 3 mismatches nel caso di stringhe da 12 bit.
Il legame e il processamento degli antigeni può anche essere eseguito, non specificamente, dalle cellule APC in due modi: direttamente, con un'interazione ad affrnità molto bassa, o in modo più efficiente, cioè attraverso un recettore Fc, con forza di interazione media, se l'antigene è stato complessato da un anticorpo.
Una volta che l'antigene si lega a una cellula B o A, i peptidi sono processati per la presentazione dall'MHC. La molecola MHC è divisa in due parti: i 4 bit di destra rappresentano la parte dell'MHC al quale si lega il recettore della cellule T. I 4 bit di sinistra rappresentano il solco in cui si accomoda il peptide. Il legame avviene tra il solco dell'MHC e una metà del peptide; l'altra metà del peptide è ciò che vedrà la cellula T. Quindi, come è schematizzato nella parte destra della figura 11, la cellula T vede una stringa di 8 bit costituita dai 4 bit di sinistra dell'MHC e dai 4 bit del peptide che non si sono legati all'MHC. Il recettore della cellula T può quindi legarsi a questo complesso MHC/peptide secondo le stesse regole che segue un recettore della cellula B nellegarsi a un epitopo.
Quando si verifica un legame efficace, sia la cellula T che la cellula B si dividono e generano un done del loro tipo; se la presentazione avviene da parte di una cellula A si dividerà solamente la cellula T. Una parte della progenie della cellula B diventa plasmacellule che producono anticorpi, un'altra parte diventa cellule della memoria.
Nel modello la discriminazione tra self e non self si ottiene attraverso la preselezione di una delle due popolazioni linfoidi. Mentre le cellule B vengono scelte a caso con un repertorio completo, ossia 2n tipi, dove n rappresenta il numero di bit del recettore, le cellule T devono prima passare per la selezione timica. Nel timo simulato, le cellule T vengono esposte agli autopeptidi presentati sulle cellule APC e se si legano vengono eliminate proporzionalmente alla forza con cui si legano. Il timo è un organo ad alta densità cellulare, per cui la stessa cellula T viene esposta a tutte le combinazioni possibili MHC/peptide. Se questo si verifica un numero sufficiente di volte, il timo sarà molto efficiente e la maggior parte delle cellule T autore attive verrà eliminata.
Ecco come viene eseguito un esperimento tipo: per prima cosa si popola il sistema del numero desiderato di APC e di cellule B e T. Secondo, si sceglie uno schema di iniezioni di antigene. Terzo, si procede alla simulazione vera e propria. In ogni sito vengono considerate tutte le interazioni possibili; quelle che sono limitate al tipo di entità coinvolte, possono verificarsi solamente tra le entità che si trovano nello stesso compartimento della griglia. Se una singola entità è in grado di avere più di un'interazione efficace, la scelta è determinata in modo stocastico. Dopo aver deciso tutte le interazioni, esse sono implementate contemporaneamente. A ogni tempo, nascono delle nuove cellule, sia attraverso la moltiplicazione per donazione, sia con la nascita di cellule vergini; le cellule muoiono con una data vita media. A tutte le entità viene poi data l'opportunità di diffondere nei siti adiacenti. Questo costituisce un'unità di tempo. Il procedimento può essere ripetuto per quante unità di tempo si desidera. Questa è solo una breve descrizione intesa a far comprendere meglio al lettore la natura dell'approccio. Una descrizione più dettagliata e completa si trova in P.E. Seiden e F. Celada (1992).
Uso dell'automa nell'esecuzione di esperimenti immunologici
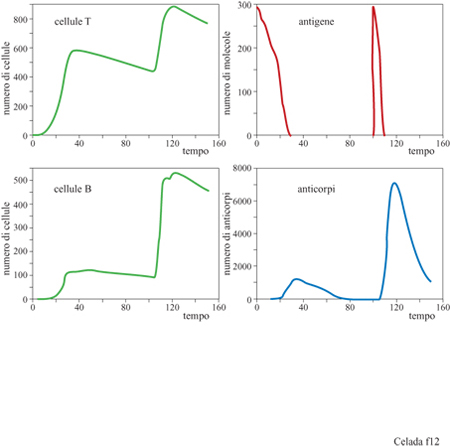
Per dimostrare che questo modello si comporta come un sistema immunitario possiamo considerare un esperimento di immunizzazione dove la stessa dose di antigene viene iniettata due volte, una prima volta a tempo 0 e una seconda volta a tempo 100 (fig. 12). Alla prima iniezione la risposta è lenta poiché la formazione dei doni delle cellule della risposta richiede tempo affrnché doni delle cellule della risposta si incontrino, dato che essi partono dai piccoli numeri delle popolazioni vergini. Viene prodotta una piccola quantità di anticorpi e gli antigeni vengono eliminati lentamente dal sistema. Con la seconda iniezione, tuttavia, vi sono molte cellule B e T della memoria che rendono rapida la risposta: vengono prodotti molti anticorpi e gli antigeni vengono eliminati abbastanza rapidamente.
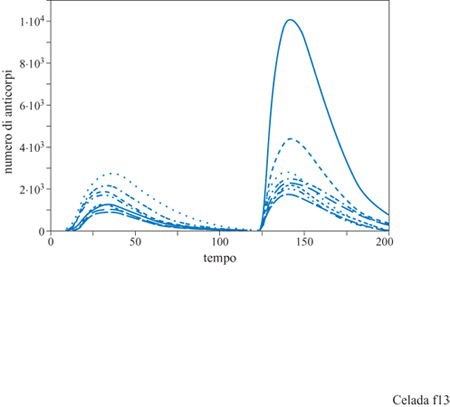
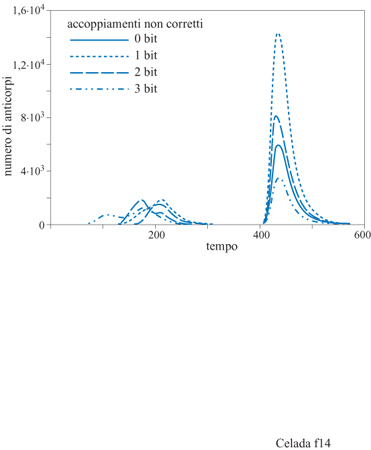
Anche questo semplice esperimento dimostra le possibilità del modello lMMSlM. La figura 12 mostra solamente la quantità totale degli anticorpi prodotti; l'esperimento è stato eseguito con recettori di 8 bit, permettendo legami sia in seguito ad accoppiamenti perfetti tra epitopi e recettori (8/8 bit) che mismatch di 1 bit (accoppiamento 7/8). L'affinità nei due casi era di l, cioè probabilità di legarsi uguale a 1 e, rispettivamente, di 0,05. Questo significa che vi sono nove diversi tipi di anticorpi: uno perfetto e otto mismatch di 1 bit. La popolazione di ciascun tipo di anticorpi è evidenziata nella figura (fig. 13). La linea continua nel grafico indica gli anticorpi ad alta affrnità (coincidenza perfetta) e le altre otto curve mostrano gli otto anticorpi a bassa affinità (mismatch di 1 bit). Gli anticorpi ad alta affinità non dominano la risposta primaria e, in effetti, molti anticorpi a bassa affinità hanno una popolazione maggiore degli anticorpi ad alta affinità. Tuttavia la risposta secondaria è dominata da anticorpi ad alta affinità, una chiara dimostrazione del fenomeno di maturazione della risposta. Questo tipo di risultato si ottiene senza aver introdotto nel modello l'ipermutazione dei recettori delle cellule B durante la crescita donale. Poiché l'esperimento è stato eseguito con un repertorio completo, ossia con tutti i tipi di recettori presenti nel sistema, non risulta necessaria la mutazione. Nella situazione biologica reale, il midollo osseo produce solo una piccola frazione dei potenziali tipi di recettori. Aggiungendo la mutazione, il modello permette lo studio di come sia la selezione sia l'ipermutazione contribuiscano a una risposta immunitaria efficiente. La figura (fig. 14) mostra i risultati di un esperimento con mutazione: sono stati utilizzati recettori da 12 bit con la possibilità di legami fino a una non complementarità per 3 bit. Anzi, in questo esperimento particolare, le uniche cellule B che vengono generate dal midollo osseo sono proprio le cellule con mismatch di 3 bit. Questo significa che tutte le cellule non complementari per 0,1 e 2 bit che si trovano alla fine della risposta sono state generate da mutazioni durante la crescita donale stimolata dall'antigene.
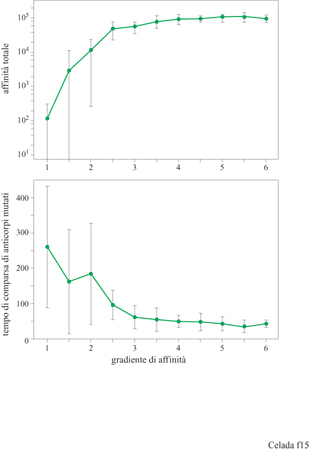
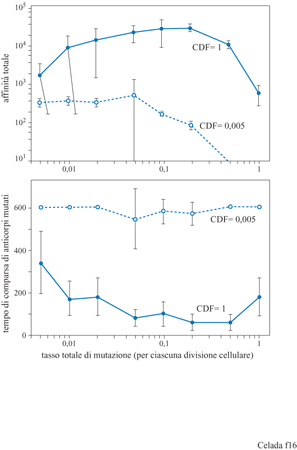
Vi sono due parametri crociali nel processo di ipermutazione e maturazione dell'affinità: la frequenza di mutazione e il gradiente di affinità, cioè il fattore che determina di quanto aumenta l'affrnità per una singola mutazione vantaggiosa. Celada e Seiden (1996) li hanno studiati avvalendosi del modello IMMSIM ed eseguendo vari esperimenti a diverse frequenze di mutazione e con diverso gradi ente di affrnità. l risultati sono mostrati nelle figure (figg. 15, 16) dove appare chiaro che, per alcuni valori dei parametri, la risposta immunitaria, anche se a volte molto ampia, può essere poco riproducibile. L'effetto della mutazione sulla maturazione dell'affinità è decisamente influenzato dal grado di focalizzazione delle mutazioni sulle aree che determinano la complementarità delle regioni variabili degli anticorpi. Per creare ipotesi alternative nel modello, abbiamo proceduto come segue. Inizialmente, tutte le mutazioni sono efficaci nel modificare i recettori e tutte influenzano l'affinità, poiché nel modello l'intero recettore entra in contatto con l'antigene. Questo assetto simula la situazione ipotetica in cui l'ipermutazione è limitata al CDR. Per rappresentare l'ipotesi opposta, abbiamo introdotto un secondo parametro chiamato CDP (Complementarity Determining Fraction), ovvero, frazione di mutazioni che è focalizzata sul CDR, che va da 1, cioè il caso descritto sopra, a 0,005, dove il 99,5% delle mutazioni si verifica fuori del CDR, nelle zone strutturali o framework. Ogni mutazione fuori dal CDR è considerata nociva per l'anticorpo ed è letale per la cellula. l risultati ottenuti per CDF = l e CDF=0,005 sono mostrati nella figura (v. figura 16). Il riquadro superiore mostra che, aumentando entro certi limiti il ritmo di mutazione, si favorisce la maturazione, come è indicato da una crescente affmità totale che culmina a circa 0,2 mutazioni per divisione cellulare per paratopo (con CDF = 1), e poi decresce rapidamente. Il riquadro inferiore mostra la prima comparsa di anticorpi mutati. L'intervallo con frequenza di mutazione tra 0,1 e 0,5 fornisce la risposta più riproducibile. l dati per CDF = 0,005 mostrano poca maturazione poiché la maggior parte dell'affinità è attribuibile ad anticorpi non mutati, ovvero con una non complementarità di 3 bit. Una piccola quantità di anticorpi mutati appare nell'intervallo con frequenza di mutazione 0,05 ÷ 0,2 ma è poco riproducibile, come si vede nella parte inferiore della figura (v. figura 16). Vi è anche un deterioramento progressivo dell' affmità totale, dovuta alla selezione negativa, per le frequenze di mutazione uguali o maggiori a 0,05. Questi risultati potrebbero essere utili per favorire una delle due alternative descritte, se fosse disponibile una misura affidabile della frequenza di mutazione in vivo. Ci auguriamo che questo si verifichi nel prossimo futuro.
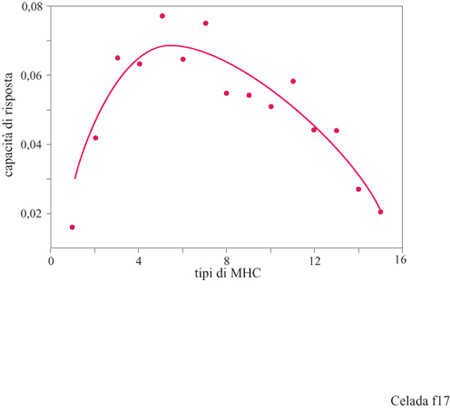
L'insieme degli esperimenti sulla maturazione dell' affinità e sull'ipermutazione sono un esempio di ciò che può fare la simulazione quando si impegna in esperimenti simili a quelli che potrebbe eseguire un immunologo lavorando in vivo o in vitro. Ora faremo un esempio di un esperimento che si può fare in machina, ma che non potrebbe eseguirsi altrettanto facilmente in laboratorio. La questione che ci poniamo è perché la varietà delle molecole MHC è molto più piccola della varietà dei recettori T e degli anticorpi, anche se appartengono tutti alla stessa classe di molecole. Per fare questo tipo di ricerca (Celada e Seiden, 1992b) è stata scelta una serie di antigeni a caso ai quali veniva esposto il sistema lMMSIM. Per tutti questi antigeni è stato misurato il livello medio di efficienza della risposta. Per ogni esperimento il sistema analizzato era caratterizzato da un numero fisso di tipi di MHC e sono stati eseguiti esperimenti per numeri di tipi di MHC da 1 a 15. I risultati sono riportati in figura (fig. 17). La curva mostra un massimo di efficienza di risposta attorno a 4 ÷ 5 MHC (per un sistema 8 bit), un piccolo numero paragonato ai 256 teorici.
La ragione di questo comportamento è il ruolo ambivalente dell'MHC che, da una parte, incrementa la risposta presentando antigeni esterni e, dall'altra, tende a limitare il repertorio della cellula T attraverso la selezione timica. In altre parole, se esiste un solo MHC, il numero di peptidi esterni che potranno essere presentati e che provocheranno una risposta sarà piuttosto piccolo. La presenza di un secondo MHC potrà alleviare questa deficienza dal momento che, in generale, un peptide non in grado di provocare risposta con il primo MHC potrebbe essere capace di farIo in presenza del secondo. Quindi, l'efficacia della risposta aumenta con l'aumentare dei tipi di MHC. Alla fine, tuttavia, il sistema finisce per mangiarsi la coda poiché ogni tipo di MHC aggiunto riduce il numero di tipi di cellule T disponibili, a causa dell'aumento del patrimonio di antigeni self, e conseguentemente della selezione negativa nel timo.
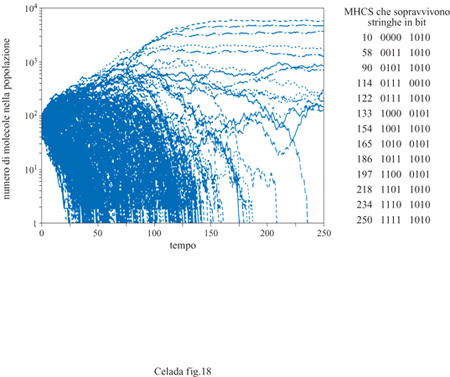
La distribuzione dei diversi tipi di MHC è notevolmente regolata in natura, ossia, oltre al fatto che gli MHC sono pochi in ogni individuo, il loro numero nell'intera popolazione è piccolo se paragonato alla varietà potenziale. Questo fenomeno è stato analizzato simulando l'evoluzione di una vasta popolazione. Sono stati creati diecimila individui, ognuno dei quali dotato di due tipi di MHC di 8 bit, scelti a caso tra il repertorio totale di 256. Gli individui possono accoppiarsi tra loro, e i nuovi nati ricevono a caso uno dei due MHC da ciascun genitore. I nostri esseri si accoppiano a caso, ma a ogni generazione il numero di individui generati da ogni coppia è proporzionale all'efficacia della risposta che i loro MHC possono fornire, calcolata separatamente per ogni combinazione di tipi MHC in esperimenti simili a quelli descritti prima. I risultati di una di queste simulazioni per 250 generazioni sono riportati graficamente nella figura (fig. 18). Si può notare che avviene una selezione darwiniana e alcuni tipi di MHC hanno più successo di altri. Dopo 250 generazioni, solo un numero limitato di tipi MHC sopravvive nella specie. L'analisi degli MHC selezionati rivela che la varietà della parte sinistra della stringa da 8 bit, l'elemento di restrizione, è di gran lunga maggiore, cioè la diversità è portatrice di un vantaggio evolutivo. Questo è giustificato dal fatto che alcune combinazioni MHC sono migliori di altre, ma anche dal netto vantaggio dell' eterozigosi. Infatti se un individuo ha due tipi MHC con la stessa parte sinistra, esso apparirebbe come quasi omozigote alla cellula T, che con il suo recettore si lega direttamente a questa area dell'MHC. Ripetendo l'esperimento con diversi numeri randomizzati, il che equivale a ripeterlo su un nuovo gruppo di animali, può cambiare la lista degli MHC sopravvissuti, generalmente tra 5 e 15, mentre l'alta varietà della metà sinistra della stringa si riproduce.
Gli esperimenti di Celada e Seiden, descritti in questo saggio, sono stati in parte finanziati dal National Institute of Health (1 ROI AI 42262-01) e dal Center for Altematives to AnimaI Testing della Johns Hopkins University. Nella stesura del saggio, F. Celada ha curato il paragrafo 'Dove si colloca il modelling?'; U. Behn, il paragrafo 'Modelli continui'; P. Seiden, il paragrafo 'Modelli discreti'.
Bibliografia citata
BEHN, U., DAMBECK, H., METZNER, G. (1998) Modelling Th1-Th2 regulation, allergy and hyposensitization. In Dynamical modelling in biotechnologies, a c. di Bagnoli F., Lio P., Ruffo S., Singapore, World Scientific.
BEHN, U., VAN HEMMEN, J.L., SULZER, B. (1993) Memory to antigenic challenge of the Immune system: synergy of idiotypic interactions and memory B cells. J. Theor. Biol., 165, 1-25.
BELL, G.I. (1970) Mathematical model of donaI selection and antibody production. J. Theor. Biol., 29, 191-232.
BELL, G.I. (1971a) Mathematical model of donaI selection and antibody production. J. Theor. Biol., 33, 339-378.
BELL, G.I. (197Ib) Mathematical model of donaI selection and antibody production. 3. The cellular basis of immunological paralysis. J. Theor. Biol., 33, 378-398.
BRADLEY, L.M., CROFT, M., SWAIN, S.L. (1993) T cell memory: new prospectives. ImmunoI. Today, 14, 197-199.
BURNETT, F.M. (1959) The clonal selection theory of immunity. Nashville, Vanderbilt University Press e Cambridge, Cambridge University Press.
CELADA, F. (1992) Computer modelling of the immune system: who are the 'Fruitors'? In Theoretical Immunology, a c. di Perelson A.S., Weisbuch G., VoI. H66, Berlino-Heidelberg, Springer Verlag.
CELADA, F., SEIDEN, P.E. (1992a) Teaching Immunology: a Montessory approach. In T Lymphocites: Structure, Functions, Choices, a c. di Celada F., Pemis B., New Y ork, Plenum Press.
CELADA, F., SEIDEN, P.E. (1992b) A computer model of cellular interactions in the immune system. ImmunoI. Today, 13, 56-62.
CELADA, F., SEIDEN, P.E. (1996) Affinity maturation and hypermutation in a simulation of the humoral immune response. Eur. J. Immunol., 26, 1350-1358.
CHOWDHURY, D., STAUFFER, D., CHOUDARY, P.V. (1990) A unified discrete model of immune response. J. Theor. Biol., 164, 207-215.
COUTINHO, A. (1989) Beyond donaI selection and network. ImmunoI. Rev., 110, 63-87.
ECO, U., SEBOEK, T.A. (1983) The sign of three: Dupin, Holmes, Peirce. Bloomington, University Press.
FREEMAN, E., SKOLIMOWSKY, H. (1974) The search for obiectivity in Pierce and PoppeI. In The Philosophy of Karl Popper, a c. di Schlipp P.A., La Salle, Open Court.
GARDNER, M. (1970) Mathematical games. Sci. Amer., 223, 120-123; 223,112-117.
JACOB, F. (1970) La nature est un bricoleur. Comunicazione privata.
JERNE, N.K. (1974) Towards a network theory of the Immune system. Ann. Immunol. (Inst. Pasteur, Parigi), 125C, 373-389.
KAUFMAN, M., URBAIN, J., THOMAS, R. (1985) Towards a logical analysis ofthe Immune response. J. Theor. Biol., 114, 527-561.
LAKATOS, I. (1974) Popper on demarcation and induction. In The Philosophy of Karl Popper, a c. di Schlipp P.A., La Salle, Open Court.
MOHLER, R.R., BRUNI, C., GANDOLFI, A. (1980) A system approach to Immunology. Proc. IEEE 68, 964-990.
MOSMANN, T.R., SAD, S. (1996) The expanding universe of T cell subsets: Th1, Th2 and more. ImmunoI. Today, 17, 138-146.
PEIRCE, C.S. (1931-1958) Collected Papers, a c. di Hartshome C., Weiss P., Cambridge, Harvard University Press.
PERELSON, A. L. , a c. di (1988) Theoretical immunology, Parts I and II, Santa Fe Institute Studies in the Science of Complexity, VolI. II, III, Redwood City, Addison-Wesley.
PERELSON, A.L., WEISBUCH, G., a c. di (1992) Theoretical, experimental insight into immunology, Cell Biology, VoI. 66, Berlino, Springer Verlag.
PERELSON, A.L., WEISBUCH, G. (1997) Immunology for physicists. Rev. Mod. Phys., 69, 1219-1268.
POPPER, K.R. (1935) Logik der Forschung zur Erkenntnistheorie der modernen Naturwissenschafi, Vienna, Julius SpringeI.
POWRIE, F., COFFMANN, R.L. (1993) Cytokine regulation of T cell function: potential for therapeutic intervention. ImmunoI. Today, 14, 270-274.
ROMAGNANI, S. (1995) Biology of human Th1 and Th2 cells. J. Clin. ImmunoI., 15, 121-129.
SEIDEN, P.E., CELADA, F. (1992) A model for simulating cognate recognition and response in the Immune system. J. Theor. BioI., 158, 329-357.
STEWART, J., VARELA, F.J. (1989) Exploring the meaning ofconnectivity in the immune network. Immunol. Rev., 110, 37-61.
SULZER, B., VAN HEMMEN, J.L., BEHN, U. (1994) CentraI Immune system, the self and autoimmunity. Bull. Math. Biol., 56, 1009-1040.
VITETTA, E.S., BERTON, M.T., BURGER, C., KEPRON, M., LEE, W.T., YIN, X.-M. (1991) Memory B and T cells. Annu. Rev. Immunol., 9, 193-217.
WOLFRAM., S. (1984) Cellular automata. Physica, 10D, VII-XII.
WOLFRAM., S. (1986) Theory and applications of Cellular Automata: including selected papers 1983-1986, Singapore, World Scientific Press.