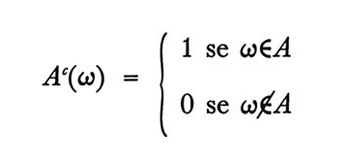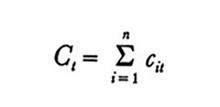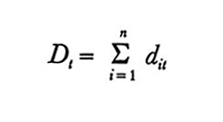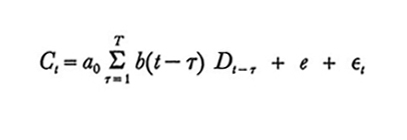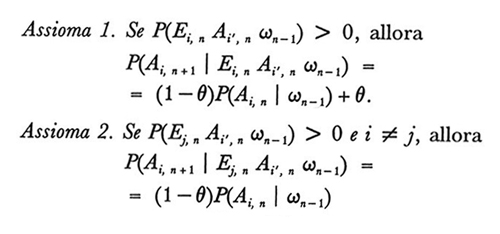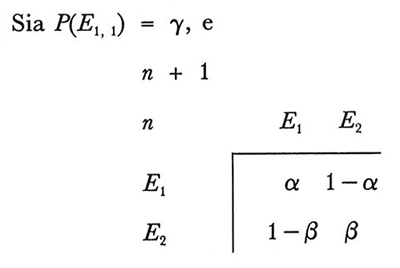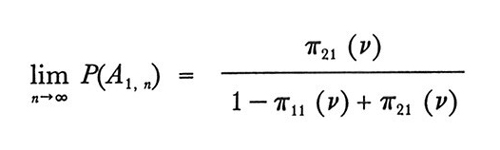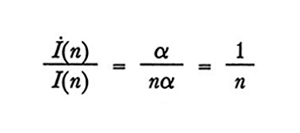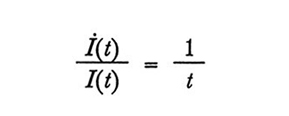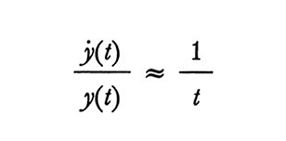Modelli

Modelli

Il significato del termine 'modello' nelle scienze

Il termine 'modello' non è usato esclusivamente in ambito scientifico, ma nei contesti più vari. Ciascuno di noi sa che cosa è il modello fisico di un edificio, di una nave, di un aeroplano. In effetti modelli del genere - specialmente modellini di aeroplani e di automobili - vengono spesso regalati ai bambini. (Modelli analoghi trovano un diffuso impiego tecnico in ingegneria). Si parla anche di eserciti modello, ordinamenti modello, e così via, quando viene soddisfatto un certo standard progettuale. In molti casi in cui si usa il termine 'modello' in questa accezione non si fa riferimento a un'entità reale: per esempio, quando si parla di governo modello non ci si riferisce a un qualche governo effettivo, ma a un insieme di requisiti che un governo ideale si pensa dovrebbe soddisfare. Una terza accezione ancora del termine 'modello' si ha quando si considera un oggetto concreto come 'esemplare' e se ne parla come di un modello di un certo tipo.

Nella maggior parte dei contesti scientifici il termine 'modello' viene raramente usato per indicare un esemplare concreto: in genere lo si usa per indicare un concetto che si avvicina molto a quello di 'standard progettuale astratto', cioè indipendente dai dettagli. Ecco alcune citazioni campione che precisano il senso in cui il termine 'modello' viene usato nei contesti scientifici."Si chiama modello di una teoria T una possibile realizzazione in cui risultino soddisfatti tutti gli enunciati validi di T" (v. Tarski, 1953, p. 11)."Quindi il modello di scelta razionale costruito a partire da confronti a due a due non sembra ben adattarsi al caso del comportamento razionale considerato nella situazione di gioco descritta" (v. Arrow, 1951, p. 21.).

"Nel costruire il modello noi assumeremo che ogni variabile sia un qualche tipo di media o di aggregato dei valori relativi ai membri del gruppo. Per esempio D potrebbe essere misurata collocando le opinioni dei membri del gruppo su una scala, assegnando dei numeri alle posizioni lungo la scala e calcolando la deviazione standard delle opinioni dei membri del gruppo in termini di questi numeri. Anche le variabili intermedie, benché non misurate direttamente, possono essere pensate come medie dei valori relativi ai singoli membri" (v. Simon, 1957, p. 116).

"Questo lavoro sui modelli matematici dell'apprendimento non ha cercato di formalizzare un qualche particolare sistema teorico di comportamento, anche se l'influsso delle teorie di Guthrie e Hull è assai evidente. In confronto con i precedenti tentativi di teorizzazione matematica, il lavoro recente è stato maggiormente indirizzato ad analisi dettagliate dei dati rilevanti per i modelli e al progetto di esperimenti per verificare direttamente previsioni quantitative fatte sulla base dei modelli" (v. Bush ed Estes, 1959, p. 3).

È prassi ampiamente diffusa in statistica matematica e nelle scienze sociali usare il termine 'modello' per indicare l'insieme delle ipotesi quantitative della teoria, cioè l'insieme degli enunciati che in una specifica trattazione saranno assunti come assiomi o che, se non si tratta di enunciati sufficientemente espliciti, costituiranno la base intuitiva per formulare un insieme di assiomi. In econometria il termine 'modello' viene impiegato in un'accezione tecnica particolare: in questo senso un modello è ciò che per i logici è una classe di modelli, e ciò che i logici chiamano 'modello' è chiamato 'struttura' dagli econometristi.

Nonostante le diverse accezioni del termine, si può dimostrare che il concetto di modello formulato da Tarski può essere adottato senza modifiche come concetto fondamentale in tutte le discipline cui si riferiscono le citazioni sopra riportate. In questo senso il concetto di modello è lo stesso in matematica e nelle scienze empiriche. La differenza fra queste discipline risiede nell'uso che fanno del concetto in questione. Nel tracciare questo confronto tra costanza di significato e differenza d'uso la questione semantica, talvolta difficile, di come si possa spiegare il significato di un concetto senza far riferimento al suo uso non si solleva. Noi useremo il concetto di modello sempre nell'ambito di contesti tecnici ben definiti. Dato questo significato tecnico del concetto di modello, i matematici si pongono un certo tipo di quesiti sui modelli, mentre gli scienziati empirici tendono a porsene di tipo diverso.

I modelli nelle scienze sociali. La citazione tratta da Arrow esemplifica, nell'ambito delle scienze sociali, una analoga, necessaria tendenza a un'estrema semplificazione. Arrow fa riferimento al modello di scelta razionale perché la teoria che ha in mente non fornisce una descrizione adeguata dei fenomeni che tratta, ma solo uno schema molto semplificato. Le stesse osservazioni valgono nel caso della citazione tratta da Simon. In Simon viene esemplificato un ulteriore fenomeno, molto comune nelle scienze sociali e del comportamento: si formula una certa teoria in termini ampi e generali; si effettuano alcuni esperimenti qualitativi per saggiare la teoria; quindi, in caso di successo di questi esperimenti, gli scienziati interessati a teorie più quantitative ed esatte si dedicano a quella che viene chiamata 'la costruzione di un modello' per la teoria originaria. Nel linguaggio dei logici sarebbe più appropriato dire che, piuttosto che a costruire un modello, essi sono interessati a costruire una teoria quantitativa in cui tradurre le idee intuitive della teoria originale. Nella citazione tratta da Bush ed Estes viene introdotta un'importante nozione, collegata, di fatto, molto strettamente al concetto di modello usato dai logici. Si tratta della nozione di modello impiegata in statistica matematica, specialmente nella vasta letteratura riguardante la stima dei parametri nei modelli e la verifica delle ipotesi su di essi. Generalmente è semplice tradurre una trattazione statistica della stima dei parametri di un modello in una in cui l'uso dei termini è in completo accordo con quello dei logici. L'analisi dettagliata di questioni statistiche richiede che si considerino i modelli quasi come entità matematiche o insiemi astratti piuttosto che come semplici entità fisiche. La domanda 'in che misura il modello si adatta ai dati?' è una domanda naturale per gli statistici e gli scienziati sociali.

Isomorfismo tra modelli

Uno dei concetti più generali e utili applicabili a una teoria è quello di isomorfismo tra due modelli della teoria. In termini generali due modelli di una teoria sono isomorfi quando presentano la stessa struttura dal punto di vista dei concetti fondamentali della teoria. Il compito cruciale della definizione formale di isomorfismo per una teoria particolare consiste nel rendere precisa questa nozione di stessa struttura.

A titolo di esempio possiamo considerare la teoria ordinale della misura. I modelli di questa teoria sono chiamati usualmente 'ordinamenti deboli'. La struttura insiemistica astratta dei modelli di questa teoria è un insieme non vuoto A e una relazione binaria R definita su questo insieme. Chiamiamo una tale coppia A = (A, R) struttura di relazione semplice. Si ha quindi la definizione seguente.

Definizione 1. Una struttura di relazione semplice A = (A, R) è un ordinamento debole se e solo se, per ogni x, y e z in A,

Se xRy e yRz allora xRz,
XRy o yRx

La definizione di isomorfismo tra strutture di relazione semplice dovrebbe essere evidente, ma viene fornita esplicitamente per maggior chiarezza, e va sottolineato il fatto che la definizione di isomorfismo dipende solo dalla struttura insiemistica astratta delle strutture di relazione semplice e non dall'imposizione di assiomi indipendenti.

Definizione 2. Una struttura di relazione semplice A = (A, R) è isomorfa a una struttura di relazione semplice A′ = (A′, R′) se e solo se esiste una funzione f tale che

Il dominio di f sia A e il codominio di f sia A′,
F sia una funzione iniettiva,

3) se x e y sono in A, allora xRy se e solo se f(x)R′f(y). Per illustrare questa definizione di isomorfismo consideriamo la domanda: 'sono isomorfi due qualsiasi ordinamenti deboli finiti con lo stesso numero di elementi?'. Intuitivamente sembra chiaro che la risposta dovrebbe essere negativa, perché in uno degli ordinamenti deboli tutti gli oggetti potrebbero stare nella relazione R con ogni altro e nell'altro no. È interessante chiedersi quale sia il controesempio col dominio più piccolo che possiamo costruire per mostrare che un tale isomorfismo non esiste in generale. È subito chiaro che due insiemi con un solo elemento non rispondono allo scopo, perché, a meno di un isomorfismo, esiste solo un ordinamento debole con un singolo elemento: l'ordinamento in base al quale quell'unico elemento sta nella data relazione R con se stesso. Tuttavia si può trovare un controesempio aggiungendo un solo elemento. Supponiamo che la relazione di uno dei due ordinamenti deboli sia la relazione universale, cioè R = A × A, il prodotto cartesiano di A con se stesso, e la relazione dell'altro sia una relazione 'minimale' soddisfacente gli assiomi di un ordinamento debole, per esempio R′ = {(1, 1), (2, 2), (1, 2)}. In questo caso si verifica facilmente che A = (A, R) e A′ = (A′, R′) sono entrambi ordinamenti deboli con domini di cardinalità due, ma A non può essere isomorfo a A′.

Teoremi di rappresentazione

Il concetto di isomorfismo ha un ruolo cruciale quando si tratta di caratterizzare la natura dei modelli di una teoria. Forse la caratterizzazione migliore e più potente dei modelli di una teoria è espressa in termini di un teorema di rappresentazione significativo. Per teorema di rappresentazione per una teoria si intende quanto segue. Si mostra che una certa classe di modelli di una teoria, che si distinguono per una qualche ragione concettuale intuitivamente chiara, esemplifica, a meno di un isomorfismo, ogni modello della teoria. Più precisamente, sia M l'insieme di tutti i modelli di una teoria e sia B un qualche sottoinsieme distinto di M. Un teorema di rappresentazione per M rispetto a B dovrebbe consistere nell'asserzione che, dato un qualsiasi modello M in M, esiste un modello in B isomorfo a M. In altre parole, dal punto di vista della teoria ogni possibile cambiamento di modello è esemplificato all'interno dell'insieme ristretto B. È chiaro che si può sempre dimostrare un teorema di rappresentazione banale prendendo B = M. Un teorema di rappresentazione è interessante soltanto nella misura in cui lo è il significato intuitivo della classe B dei modelli. Un esempio di teorema di rappresentazione semplice ed elegante è il teorema di Cayley secondo cui ogni gruppo è isomorfo a un gruppo di trasformazioni. Il concetto di gruppo, quale è stato formulato nel XIX secolo, ha avuto origine, fra l'altro, dallo studio delle funzioni iniettive da un insieme a se stesso. Tali funzioni sono chiamate, in genere, 'trasformazioni'. È interessante e sorprendente il fatto che gli assiomi elementari della teoria dei gruppi bastino a caratterizzare le trasformazioni in questo senso astratto, cioè che si possa mostrare che un qualsiasi modello degli assiomi, ovvero un gruppo qualsiasi, è isomorfo a un gruppo di trasformazioni (per una discussione e una dimostrazione di questo teorema v. Suppes, 1957, cap. 12).

Certi casi di teoremi di rappresentazione rivestono un interesse speciale. Quando si può prendere come insieme B un insieme costituito da un solo elemento, allora si dice che la teoria è 'categorica'. In altri termini una teoria è categorica quando due suoi modelli qualsiasi sono isomorfi. Pertanto una teoria categorica in realtà ha, a meno di un isomorfismo, un solo modello. Esempi di teorie categoriche sono la teoria elementare dei numeri, quando si impiega un concetto standard di insieme, e la teoria elementare dei numeri reali, quando si impiega lo stesso concetto standard di insieme.

Da un punto di vista psicologico si può probabilmente dimostrare che una teoria è considerata astratta quando la classe dei suoi modelli diventa tanto ampia che non è possibile fornire una qualche immagine, o raffigurazione, semplice di un suo modello tipico. La gamma dei modelli è troppo diversificata; la teoria è altamente non categorica. Un altro significato dell'aggettivo 'astratto', strettamente collegato al precedente, è quello secondo cui certe proprietà intuitive e spesso, forse, complesse del modello originale della teoria sono state tralasciate - come nel caso dei gruppi - e si passa a parlare di modelli che soddisfano una teoria anche se essi hanno una struttura interna molto più semplice del modello intuitivo originario. Questo significato del termine 'astratto' è molto vicino a quello etimologico.

Omomorfismo tra modelli. In molti casi di pertinenza della matematica pura un teorema di rappresentazione formulato in termini di isomorfismo tra modelli si rivela meno interessante di un teorema di rappresentazione espresso in termini della nozione, più debole, di omomorfismo. Un buon esempio di un caso del genere nell'ambito delle scienze sociali è fornito dalle teorie della misurazione, e la generalizzazione dall'isomorfismo all'omomorfismo può essere illustrata nel contesto di tali teorie. Quando consideriamo operazioni di misurazione generali è evidente che, in base al concetto strutturale di isomorfismo, noi saremmo indotti a pensare, a prima vista, che l'isomorfismo intercorra tra un modello empirico della teoria della misurazione e un modello numerico. Per modello empirico intendiamo un modello in cui l'insieme fondamentale è un insieme di oggetti empirici e per modello numerico un modello in cui l'insieme fondamentale è un insieme di numeri. Ma un esame appena un po' più dettagliato della questione evidenzia che ben presto insorgono difficoltà circa l'isomorfismo. Nella stragrande maggioranza dei casi in cui si effettuano misurazioni a oggetti fisici distinti viene assegnato lo stesso numero e quindi la relazione iniettiva richiesta per l'isomorfismo tra modelli non sussiste. Fortunatamente questo indebolimento del requisito della iniettività per l'isomorfismo è l'unico aspetto della nozione generale che dobbiamo cambiare per ottenere, nel caso delle teorie della misurazione, una definizione adeguata del rapporto tra modelli empirici e modelli numerici.

Tipi di modelli

Nelle scienze fisiche si è soliti, per antica tradizione, derivare da ipotesi empiriche qualitative o quantitative le equazioni differenziali che governano, almeno in prima approssimazione, una gran varietà di fenomeni fisici. I procedimenti di derivazione di alcune di queste equazioni - per esempio delle equazioni di Navier-Stokes per i fluidi idrodinamici - vanno annoverati fra le analisi concettuali più importanti della storia della fisica. La formulazione di equazioni differenziali classiche è molto importante anche nella routine quotidiana delle scienze fisiche, nel cui ambito si derivano equazioni specifiche per rappresentare matematicamente particolari circostanze che possono avere in sé una considerevole rilevanza pratica, pur senza rivestire un interesse scientifico universale. Di importanza fondamentale per le applicazioni delle teorie fisiche ai fenomeni empirici è la lunga e feconda tradizione di tali procedimenti di derivazione.

Metodi analoghi non sono altrettanto ben sviluppati nelle scienze sociali, e basta passare in rassegna le principali pubblicazioni del settore, nelle quali vengono proposti e verificati modelli, per rendersi conto che la formulazione di equazioni differenziali non domina assolutamente la derivazione dei modelli nell'ambito delle scienze sociali.

In questo articolo sono presi in esame quattro differenti tipi di modelli: le rappresentazioni in termini di misure, i modelli di regressione, i modelli osservabili non markoviani con ipotesi di processo e, infine, i modelli costituiti dalle equazioni differenziali classiche, così caratteristici delle scienze fisiche.

Rappresentazioni in termini di misure

In quasi tutte le discipline scientifiche si sa che senza misura non può esservi né un controllo preciso né una previsione dei fenomeni. Nell'ambito di discipline, come, in primo luogo, le scienze sociali, che non hanno una lunga tradizione di teorie quantitative la formulazione di una teoria della misurazione può svolgere un ruolo centrale nell'indagine scientifica. Possiamo descrivere questa attività generale come la costruzione di modelli di misurazione in cui relazioni e operazioni empiriche qualitative che possono essere trattate sperimentalmente in modo esplicito costituiscono la base di una teoria assiomatica qualitativa di procedimenti di misurazione. Da un punto di vista sperimentale o empirico il problema consiste nel mostrare fino a che punto gli assiomi postulati possano effettivamente essere verificati sperimentalmente. Da un punto di vista formale, d'altra parte, il compito principale consiste nel mostrare che gli assiomi sono formalmente adeguati, cioè che, per ogni realizzazione delle relazioni e delle funzioni qualitative che sono alla base degli assiomi empirici, si può derivare una rappresentazione in termini di misure numeriche. L'argomento ha una lunga storia che non può essere tratteggiata in questa sede. Analizzeremo un solo, ma significativo, esempio, e precisamente gli sforzi per capire gli ordinamenti di probabilità qualitativi. Sia per motivi di interesse psicologico - quali risultano riflessi nello studio empirico delle credenze e delle decisioni - sia per ragioni normative, legate agli approcci bayesiani alla statistica, la teoria delle relazioni di probabilità qualitative ha ormai raggiunto un grado di sviluppo assai elevato. Per dare un'idea di come vengano costruite e studiate le rappresentazioni in termini di misure basta considerare l'esempio seguente, che tralascia ogni questione riguardante la misura dell'utilità e si concentra interamente sulla misura della probabilità soggettiva.

Sia Ω un insieme non vuoto e sia ℑ un'algebra di eventi su Ω, cioè un'algebra di insiemi su Ω. Sia ≥ un ordinamento qualitativo su ℑ. L'interpretazione di A ≥ B per due eventi A e B è che A sia almeno tanto probabile quanto B. Una misura di probabilità (finitamente additiva) P su ≥ è strettamente corrispondente alla relazione ≥ se e solo se per ogni coppia di eventi A e B in ℑ si ha

P(A)  ≥ P(B) se e solo se A ≥ B.

Sono note svariate condizioni che garantiscono l'esistenza di una misura strettamente corrispondente. Senza voler fornire una classificazione precisa, diciamo che gli insiemi di condizioni sono del tipo seguente: a) condizioni sufficienti ma non necessarie per l'esistenza di una misura unica quando l'algebra degli eventi è infinita (v. Koopman, 1940; v. Savage, 1954; v. Suppes, 1956); b) condizioni sufficienti ma non necessarie per l'unicità quando l'algebra degli eventi è finita o infinita (v. Luce, 1967); c) condizioni sufficienti ma non necessarie per l'unicità quando l'algebra degli eventi è finita (v. Suppes, 1969); d) condizioni necessarie e sufficienti per l'esistenza di una misura non necessariamente unica quando l'algebra degli eventi è finita (v. Kraft e altri, 1959; v. Scott, 1964; v. Tversky, 1967). Una discussione alquanto dettagliata di questi vari insiemi di condizioni si trova in Krantz e altri (v., 1971, capp. 5 e 9).Una vasta letteratura, tuttora in crescita, mostra che è difficile fornire semplici condizioni qualitative necessarie e sufficienti solo in termini di eventi. D'altra parte una semplificazione è relativamente facile se si introducono alcuni concetti ausiliari (v. Suppes e Zanotti, 1976). Nel caso in esame si tratta di passare da un'algebra degli eventi a un'algebra delle funzioni indicatrici estese degli eventi. Con quest'ultimo concetto intendiamo quanto segue. Come sopra sia Ω l'insieme dei possibili risultati e sia ℑ un'algebra di eventi su Ω, cioè una famiglia non vuota di sottoinsiemi di Ω. Inoltre ℑ sia chiusa rispetto all'operazione di passaggio al complementare e all'unione, cioè sia tale che, se contiene A, contenga anche ¬A - il complemento di A in Ω - e, se contiene A e B, contenga anche A∪B. Sia A^c la funzione indicatrice (o funzione caratteristica) dell'evento A.

Ciò significa che A^c è una funzione definita su Ω tale che per ogni ω in Ω si ha

L'algebra ℑ* delle funzioni indicatrici estese relative a ℑ è quindi proprio il più piccolo semigruppo (additivo) contenente le funzioni indicatrici di tutti gli eventi in ℑ. In altre parole ℑ* è l'intersezione di tutti gli insiemi dotati della proprietà che, se A è in ℑ, allora A^c è in ℑ* e, se A* e B* sono in ℑ*, allora A* + B* è in ℑ*. È facile mostrare che una qualsiasi funzione A* in ℑ* è una funzione a valori interi definita su Ω. È l'estensione dalle funzioni indicatrici alle funzioni a valori interi che giustifica il fatto di chiamare gli elementi di ℑ* 'funzioni indicatrici estese'. Gli ordinamenti di probabilità qualitativi devono essere estesi da ℑ a ℑ* e va considerata la giustificazione intuitiva di questa estensione. Siano A* e B* due funzioni indicatrici estese in ℑ*. Allora il fatto che sia A* ≥ B* significa che il valore atteso di A* è maggiore o uguale al valore atteso di B*. Come dovrebbe esser chiaro, le funzioni indicatrici estese non sono altro che variabili casuali di tipo ristretto. Il confronto qualitativo, quindi, non avviene più fra le probabilità che si verifichino gli eventi, ma fra i valori attesi di certe variabili casuali ristrette. A loro volta le funzioni indicatrici costituiscono, naturalmente, una classe ancor più ristretta di variabili casuali, ma il confronto qualitativo fra i loro valori attesi è concettualmente identico al confronto qualitativo fra le probabilità che si verifichino gli eventi.

Gli assiomi sono incorporati nella definizione di algebra qualitativa di funzioni indicatrici estese. Alcuni punti relativi alla notazione adottata richiedono un chiarimento. In primo luogo Ω^c e ∅^c sono le funzioni indicatrici o caratteristiche dell'insieme Ω dei possibili risultati e dell'insieme vuoto ∅, rispettivamente. In secondo luogo la notazione nA* per una funzione in ℑ* non è altro che la notazione standard per indicare la somma (funzionale) di A* con se stessa n volte. In terzo luogo si usa la stessa notazione per indicare la relazione d'ordine su ℑ e la relazione d'ordine su ℑ*, perché quella su ℑ* è un'estensione di quella su ℑ: per A e B in ℑ si ha

A ≥ B se e solo se A^c ≥ B^c.

Infine la relazione d'ordine in senso stretto > è definita nel solito modo: A* > B* se e solo se A* ≥ B* e non B* ≥A.

Definizione 3. Sia Ω un insieme non vuoto, sia ℑ un'algebra di insiemi su Ω e sia ≥ una relazione binaria su ℑ*, l'algebra delle funzioni indicatrici estese relative a ℑ. Allora l'algebra qualitativa (Ω, ℑ*, ≥) è qualitativamente soddisfacente se e solo se i seguenti assiomi risultano soddisfatti per ogni A*, B* e C* in ℑ*.

Assioma 1. La relazione ≥ è un ordinamento debole su ℑ*.

Assioma 2. Ω^c > ∅^c.

Assioma 3. A* ≥ ∅^c.

Assioma 4. A* ≥ B* se e solo se A*+C ≥ B*+C*.

Assioma 5. Se A* >B*, allora per ogni C* e D* in ℑ* esiste un intero positivo n tale che sia

nA+C* ≥ nB*+D*.

Questi assiomi dovrebbero apparire familiari a chi conosca la letteratura sulla probabilità qualitativa. Si noti che l'assioma 4 (assioma di additività) rassomiglia molto all'assioma di additività per gli eventi di de Finetti: se A∩C = B∩C = ∅c, allora A B se e solo se A∪C B∪C. Passando dagli eventi alle funzioni indicatrici estese, l'addizione funzionale sostituisce l'unione di insiemi. L'aspetto formalmente importante di questo passaggio risulta già evidente nella formulazione esatta dell'assioma 4: l'additività delle funzioni indicatrici estese è incondizionata, non esiste una restrizione corrispondente alla condizione A∩C = B∩C = ∅. L'assenza di una tale restrizione ha importanti conseguenze formali, in quanto ci permette di applicare senza alcuna sostanziale modificazione la teoria generale de lla misurazione estesa.

Teorema. Sia Ω un insieme non vuoto, sia un'algebra di insiemi su Ω e sia una relazione binaria su . Allora una condizione necessaria e sufficiente perché esista una misura di probabilità strettamente corrispondente su è che esista un'estensione di da a * tale che l'algebra qualitativa delle funzioni indicatrici estese (Ω, *, ) sia qualitativamente soddisfacente. Inoltre la funzione di aspettativa su * è unica.Non è possibile in questa sede fornire la dimostrazione del teorema enunciato, che è data in Suppes e Zanotti (v., 1976), dove è riportata anche gran parte della discussione precedente. Il fatto importante è che nella dimostrazione del teorema si usano in modo esplicito risultati standard della teoria generale della misura estesa. L'estensione al caso della probabilità si trova in Suppes e Zanotti (v., 1982).

Modelli di regressione

Per illustrare le idee che sono alla base di questi modelli esaminiamo un'analisi delle cause dei livelli di consumo, fatta in termini di reddito individuale disponibile in una data popolazione. In questo genere di analisi, tipico del metodo della regressione, non si pretende che l'ammontare del reddito disponibile sia l'unica causa del livello di consumo, ma quasi tutti si aspettano che ne sia una delle cause principali. La questione interessante è se il consumo attuale sia influenzato dal reddito disponibile passato.

Per esaminare alcuni modelli poniamocit = consumo nel periodo t da parte dell'individuo o della famiglia i;

dit = reddito a disposizione di i nel periodo t, e, per aggregazione di n individui,

e

(Per una buona discussione di tale aggregazione e di altri aspetti metodologici dei modelli considerati in questo paragrafo, v. Malinvaud, 1966, cap. 4).

In termini della notazione definita un ovvio modello lineare è

formula (1)

dove a₀ ed e sono costanti, b(t-τ) è una costante per il periodo t - τ ed εt è il termine di errore per il periodo t. Nella formulazione probabilistica usuale si assume che l'aspettativa di εt sia zero.

Uno studio classico di Friedman (v., 1957) sui dati annuali relativi al consumo e al reddito a disposizione dei capifamiglia negli Stati Uniti nel periodo 1905-1951 - esclusi gli anni di guerra - conduce alla seguente versione numerica della (1):

C_t = 0.29D_t + 0.19D_t-1 + 0.13D_t-2 + 0.09D_t-3 + 0.06D_t-4 + 0.04D_t-5 - 4. (2)

L'aspetto da sottolineare nel presente contesto è che nella maggior parte degli studi empirici di economia si usano come modelli gli ovvi tipi di modelli di regressione lineare esemplificati dalle equazioni (1) e (2). Non si pretende quasi mai che tali modelli rappresentino esattamente i fenomeni in questione. Quel che è importante è che tali modelli di regressione lineare rendano conto di buona parte delle variazioni dei fenomeni. Generalmente il modo corretto di concepire i modelli di regressione consiste nel considerarli il punto di inizio di un'analisi con la conclusione. D'altra parte spesso essi riescono a render conto di un'alta percentuale di variazione dei fenomeni e quindi la ricerca di modelli più dettagliati è, per molti scopi, meno importante di quanto potrebbe sembrare.

Modelli osservabili non markoviani con ipotesi di processo

Il modello di apprendimento lineare che prenderemo a esempio è stato ampiamente utilizzato nella psicologia matematica e anche nello sviluppo dell'ingegneria dei processi di controllo. Esamineremo il modello da un punto di vista concettuale nei termini dell'apprendimento di un organismo. Supporremo inoltre che la situazione si risolva in una serie discreta di tentativi, anziché in un continuo temporale, ma anche la generalizzazione al continuo temporale è interessante.

Per semplicità supponiamo che a ogni tentativo l'organismo possa dare esattamente una tra due risposte, A₁ o A₂, e che dopo ogni risposta esso riceva il rinforzo, E₁ o E₂, di una delle due risposte possibili. Un parametro di apprendimento θ, che è un numero reale tale che 0 ⟨ θ ≤ 1, descrive il tasso di apprendimento in un modo che definiremo fra breve. Una possibile realizzazione della teoria è una terna ordinata (Ω, P, θ) del tipo seguente. Ω è l'insieme di tutte le sequenze di coppie ordinate tali che il primo membro di ogni coppia è un elemento di un certo insieme A e il secondo membro un elemento di un certo insieme B, entrambi contenenti due elementi. Intuitivamente l'insieme A rappresenta le due possibili risposte e l'insieme B i due possibili rinforzi. P è una misura di probabilità sulla σ-algebra degli insiemi cilindrici di Ω e θ è, come già detto, un numero reale. Per definire i modelli della teoria dobbiamo introdurre alcune notazioni. Ai, n è l'evento costituito dalla risposta Ai al tentativo n; Ej, n è l'evento costituito dal rinforzo Ej al tentativo n, dove i, j = = 1, 2; dato ω in Ω, sia ωn la classe di equivalenza di tutte le sequenze in Ω che sono identiche a ω fino al tentativo n. Possiamo allora caratterizzare i modelli della teoria nel modo seguente.

Definizione 4. Una terna (Ω, P, θ) è un modello di apprendimento lineare se e solo se risultano soddisfatti i seguenti assiomi.

Come risulta chiaro dai due assiomi, la teoria della risposta lineare è intuitivamente molto semplice. Il primo assioma afferma che quando una risposta viene rinforzata la probabilità di fornire quella risposta al tentativo successivo aumenta mediante una semplice trasformazione lineare. Il secondo assioma afferma che se qualche altra risposta è rinforzata la probabilità di fornire la risposta diminuisce mediante una seconda trasformazione lineare. Questi modelli di apprendimento lineari sono esempi di catene di ordine infinito, così dette perché la dipendenza dal passato non termina dopo un periodo prefissato o un prefissato numero di tentativi. Tuttavia noi troviamo molto naturale per svariate ragioni pensare in termini di processi markoviani, in cui lo stato presente contiene tutta l'informazione necessaria sul passato, sicché è stato compiuto uno sforzo ben preciso per ridefinire il concetto di stato per tali catene di ordine infinito intese come modelli di apprendimento lineari. Quando il rinforzo dato in corrispondenza del tentativo n dipende probabilisticamente al più dalla risposta immediatamente precedente quel tentativo, allora le probabilità di risposta possono essere prese come stati, ed è facile mostrare - sotto la restrizione convenuta - che il processo è markoviano. Esempi esaurienti di questa impostazione markoviana sono presentati, insieme con la teoria generale, in Norman (v., 1972). Tuttavia questa impostazione non funziona nemmeno per la semplice tabella di rinforzo markoviana seguente.

In tal caso l'impostazione markoviana di Norman non funziona, com'è facile mostrare. Le proprietà di questo modello di apprendimento lineare sono ampiamente studiate in Estes e Suppes (v., 1959). Il modello è generalizzato a un continuo di risposte in Suppes (v., 1959).

Qui presentiamo un semplice risultato asintotico preso da Estes e Suppes (v., 1959), per illustrare il tipo di quantità testabili derivate per una data tabella di rinforzo o feedback. Sia πj, k (n) la probabilità che l'evento costituito dal rinforzo Ek si verifichi in corrispondenza del tentativo n, posto che la risposta Aj sia stata data ν tentativi prima. Allora si ha

Modelli continui

Si è già accennato all'importanza della derivazione di equazioni differenziali nelle scienze fisiche e in una vasta gamma di applicazioni in ingegneria. Tali derivazioni di equazioni differenziali svolgono un ruolo anche nelle scienze sociali, più nell'ambito dell'economia che altrove, ma vi sono svariati esempi di equazioni differenziali, e delle rispettive derivazioni da ipotesi empiriche o da principî, anche in psicologia e in sociologia. Qui presentiamo un esempio tratto dalla psicologia pedagogica, che mostra anche parecchie caratteristiche dell'uso delle equazioni differenziali nelle scienze fisiche. Per esempio il fatto che, pur essendo i fenomeni in esame discreti, ai fini dell'analisi è ragionevole derivare un'equazione differenziale per l'approssimazione continua dei fenomeni.

Alla base della particolare applicazione qui considerata c'è il desiderio di poter predire i progressi di uno studente che frequenti un corso, specie se si tratta di un corso basato sull'impiego del computer e, per di più, individualizzato. Il metodo classico di valutazione di un nuovo programma di studi nelle scuole presenta un importante aspetto insoddisfacente. Questo tipo di valutazione si effettua confrontando i test eseguiti prima dello svolgimento del programma e quelli eseguiti dopo con un'analisi delle distribuzioni dei punteggi ottenuti dopo lo svolgimento del programma in funzione della distribuzione ottenuta prima dello svolgimento del programma e dell'esecuzione del programma stesso. L'aspetto insoddisfacente risiede nel carattere a posteriori della valutazione, cioè nel fatto che si debbano attendere i risultati per poterla effettuare. Viceversa un tratto peculiare delle scienze fisiche consiste nella ricerca continua di modelli capaci di predire i fenomeni e suscettibili di essere usati a fini di controllo, come accade in ingegneria. Qui consideriamo proprio un modello del genere, applicato all'analisi dei progressi di uno studente in un corso di studi, che sintetizza i risultati di una ricerca protrattasi per molti anni, a cominciare dal lavoro di Suppes, Fletcher e Zanotti (v., 1976).

Supponiamo, come già specificato, che il corso frequentato dallo studente sia individualizzato. Sia I(t) la quantità totale di informazione presentata allo studente fino al tempo t. (L'espressione informazione totale potrebbe essere sostituita da una formulazione fatta in termini di capacità acquisite e noi potremmo valutare i progressi sotto il profilo procedurale anziché espositivo). Sia y(t) la posizione dello studente nel corso al tempo t. Si noti che per semplicità di notazione non abbiamo utilizzato un indice per identificare un particolare studente. È inteso che la notazione usata qui si applica soltanto a uno studente singolo, non a medie di studenti. La media stocastica in gioco è la media delle varie capacità o informazioni presentate allo studente, media che indica la sua posizione media e la sua informazione media. Non espliciteremo ulteriormente queste ipotesi stocastiche, perché in questa sede ci limiteremo a sviluppare la teoria media per il singolo studente.

La prima ipotesi è che il processo sia additivo e dipenda, per semplicità concettuale, da una variabile discreta n. Possiamo scrivere l'ipotesi di additività come segue:

I(n) - I(n-1) = α. (3)

Possiamo poi esprimere la (3) nella forma seguente, in cui compare la derivata temporale:

formula  (4)

Infine, introducendo la variabile temporale continua t, la (4) viene sostituita dalla (5),

formula  (5)

Introduciamo quindi la seconda ipotesi forte, e cioè che la posizione nel corso sia proporzionale all'informazione fornita:

y(t) ≈ I(t).  (6)

Combinando la (5) e la (6) otteniamo l'equazione (7),

formula  (7)

che possiamo integrare ottenendo l'equazione (8),

lny(t) = klnt + lnb (8)

equivalente alla (9):

y(t) = bt^k (9)

L'equazione (9) è stata applicata all'analisi dei dati relativi a studenti frequentanti svariati corsi basati sull'impiego del computer.

Alcune questioni generali

Assiomatica. È stato osservato in diverse occasioni che l'uso di metodi assiomatici è più comune nelle scienze sociali che in quelle fisiche. A questa osservazione è stata in genere attribuita una connotazione leggermente negativa. Ciò che è stato messo in rilievo in questo articolo è la derivazione e la formulazione di vari modelli piuttosto che il puro uso di metodi assiomatici, qual è riflesso negli enunciati espliciti e precisi delle teorie generali. L'esempio della misura, presentato nel § 4a, illustra il metodo assiomatico in forma pura. Viceversa l'ultimo esempio, in cui si deriva una funzione per prevedere i progressi conseguiti da uno studente in un corso, non è veramente assiomatico nella forma, ma è assimilabile ai casi classici di derivazione di equazioni differenziali, fatta sulla base di particolari ipotesi. Il punto essenziale, al riguardo, è che le ipotesi empiriche da cui vengono derivate le equazioni differenziali non sono elevate al rango di assiomi di una teoria generale. Si tratta di una distinzione riconosciuta nell'ambito delle scienze fisiche, ma che non è importante rendere del tutto precisa. In presenza di una situazione fisica nuova, per esempio il moto di un braccio meccanico, è importante derivare le equazioni del moto a partire dai vincoli fisici dati, ma in genere non attribuiamo lo status di assiomi alle formulazioni delle ipotesi fisiche relative al particolare braccio meccanico in esame. Lo stesso discorso vale per molti dei modelli discussi sopra. Soprattutto non esiste alcun processo di effettiva derivazione da assiomi nel caso del modello di regressione lineare discusso e questo fatto è caratteristico di molte applicazioni della regressione lineare, seppure non di tutte.

È anche importante riconoscere che esiste una lunga tradizione metodologica in base alla quale si inizia l'analisi dei fenomeni dai loro aspetti più superficiali e apparenti, per poi cercare di derivare le equazioni che li descrivono da qualche ipotesi più fondamentale. Questo modo di procedere è stato adottato da Estes e Suppes (v., 1974) nel caso dei modelli di apprendimento lineare discussi sopra, assumendo che il numero degli stimoli campionati tenda asintoticamente all'infinito, sotto alcune ipotesi restrittive su come questo tendere all'infinito abbia luogo. Il modello di apprendimento lineare può quindi essere derivato, al limite, da un modello che campiona gli stimoli. Ma questo tipo di ricerca di base, per quanto importante, non è al centro della presente trattazione e probabilmente per la maggior parte degli scopi scientifici non è tanto importante quanto la possibilità di disporre di svariati metodi per derivare modelli che possano essere testati direttamente.

L'uso di variabili teoriche non osservabili. In contrasto con l'ultima osservazione sull'assiomatica, va sottolineata l'importanza di sviluppare teorie che penetrino sotto la superficie dei fenomeni. Una lunga storia di successi nel campo della fisica indica l'importanza di questo fatto. Lo stesso discorso sembra valere per i modelli nelle scienze sociali. Nel caso degli esempi discussi, che riguardano l'apprendimento e la cognizione, è evidente che il nostro ragionamento scientifico andrà, quasi naturalmente, al di là dei dati meramente osservabili. Sembra anche molto probabile che i meccanismi interni e i concetti teorici relativi che li caratterizzano resteranno non osservabili nei dettagli per un tempo imprecisabile, se non addirittura per sempre, nel caso della maggior parte dei processi cognitivi dell'uomo. Qualsiasi progetto di eliminazione delle variabili teoriche non osservabili appare del tutto sbagliato e contrario a quasi tutti gli sviluppi più profondi della psicologia scientifica contemporanea, per non parlare dell'importante ruolo svolto dalle ipotesi riguardanti le ipotesi non verificate e spesso non verificabili concernenti le scelte e le preferenze individuali nella teoria economica neoclassica.

L'importanza delle misurazioni. D'altronde va sottolineata l'importanza delle misurazioni nelle scienze sociali, dove procedimenti del genere non hanno alle spalle una lunga storia di perfezionamenti come nelle scienze fisiche. Problemi di misurazione sono presenti in tutte le scienze sociali e la teoria necessita di un progresso costante. È anche importante rendersi conto che spesso questi progressi non sono fatti semplicemente in termini di variabili fenomenologiche, ma anche in termini di concetti teorici. Forse il più significativo di tali concetti è quello di utilità nell'ambito della teoria delle decisioni, ampiamente usato in economia e in psicologia. Gli assiomi dell'utilità, o dell'utilità attesa, non sono direttamente osservabili, nella forma in cui vengono usualmente enunciati, e al concetto di funzione di utilità individuale deve essere attribuito uno status teorico. Ciò non significa che la misurabilità di questo concetto teorico non sia di grande importanza, poiché dalla teoria della sua misurazione possono essere derivate molte conseguenze osservabili.

La teoria della misurazione, proprio a causa dello sviluppo relativamente recente dei metodi di misurazione nelle scienze sociali, riveste tuttora grande importanza e senza dubbio continuerà a prosperare, e, soprattutto, continuerà a essere la fonte da cui trarranno origine molti modelli nelle scienze sociali. D'altra parte la derivazione di modelli nelle scienze sociali non può in alcun modo essere ridotta semplicemente a problemi di misurazione. Le teorie della misurazione sono importanti, ma non sono tutto. (V. anche Funzionalismo: analisi strutturalfunzionale; Statistica applicata alle scienze sociali).

Bibliografia

Arrow, K.J., Social choice and individual values, New York 1951 (tr. it.: Scelte sociali e valori individuali, Milano 1977).

Bush, R.R., Estes, W.K. (a cura di), Studies in mathematical learning theory, Stanford, Cal., 1959.

Estes, W.K., Suppes, P., Foundations of linear models, in Studies in mathematical learning theory (a cura di R.R. Bush e W.K. Estes), Stanford, Cal., 1959, pp. 137-179.

Estes, W.K., Suppes, P., Foundations of stimulus sampling theory, in Contemporary developments in mathematical psychology (a cura di D.H. Krantz, R.C. Atkinson, R.D. Luce e P. Suppes), vol. I, Learning memory and thinking, San Francisco, Cal., 1974.

Friedman, M., A theory of the consumption function, National Bureau of Economic Research, New York 1957.

Koopman, B.O., The bases of probability, in "Bulletin of the American mathematical society", 1940, XLVI, pp. 763-774.

Kraft, C.H., Pratt, J.W., Seidenberg, A., Intuitive probability on finite sets, in "Annals of mathematical statistics", 1959, XXX, pp. 408-419.

Krantz, D.H., Luce, R.D., Suppes, P., Tversky, A., Foundations of measurement, vol. I, New York 1971.

Luce, R.D., Sufficient conditions for the existence of a finitely additive probability measure, in "Annals of mathematical statistics", 1967, XXX, pp. 408-419.

Malinvaud, E., Statistical methods of econometrics, Amsterdam 1966 (tr. it.: Metodi statistici dell'econometria, Torino 1971).

Norman, M.F., Markov processes and learning models, New York 1972.

Savage, L.J., The foundations of statistics, New York 1954.

Scott, D., Measurement models and linear inequalities, In "Journal of mathematical psychology", 1964, I, pp. 233-247.

Simon, H.A., Models of man, New York 1957.

Suppes, P., The role of subjective probability and utility in decisionmaking, in Proceedings of the third Berkeley symposium of mathematical statistics and probability, vol. V, Berkeley, Cal., 1956.

Suppes, P., Introduction to logic, New York 1957.

Suppes, P., A linear model for a continuum of responses, in Studies in mathematical learning theory (a cura di R.R. Bush e W.K. Estes), Stanford, Cal., 1959, pp. 400-414.

Suppes, P., Studies in the methodology and foundations of science, Dordrecht 1969.

Suppes, P., Models and methods in the philosophy of science. Selected essays, Dordrecht 1993.

Suppes, P., Fletcher, J.D., Zanotti, M., Models of individual trajectories in computer-assisted instruction for deaf students, in "Journal of educational psychology", 1976, LXVIII, pp. 117-127.

Suppes, P., Zanotti, M., Necessary and sufficient conditions for existence of a unique measure strictly agreeing with a qualitative probability ordering, in "Journal of philosophical logic", 1976, V, pp. 431-438.

Suppes, P., Zanotti, M., Necessary and sufficient qualitative axioms for conditional probability, in "Zeitschrift für Wahrscheinlichkeitstheorie verwandelt Gebiete", 1982, LX, pp. 163-169.

Tarski, A., A general method in proofs of undecidability, in Undecidable theories (a cura di A. Tarski, A. Mostowski e R.M. Robinson), Amsterdam 1953.

Tversky, A., Additivity, utility and subjective probability, in "Journal of mathematical psychology", 1967, IV, pp. 175-201.