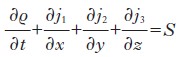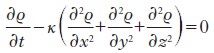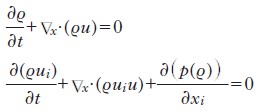MODELLISTICA DIFFERENZIALE

MODELLISTICA DIFFERENZIALE.

- Equazioni alle derivate parziali provenienti dalla modellistica. Studio qualitativo delle equazioni alle derivate parziali. Soluzioni esplicite e approssimate. Analisi asintotica delle equazioni alle derivate parziali. Bibliografia

Equazioni alle derivate parziali provenienti dalla modellistica. – Lo studio delle equazioni alle derivate parziali provenienti dalla modellistica nell’ambito delle scienze naturali o in quello dell’ingegneria è divenuto in questi ultimi anni un tema centrale della ricerca in matematica applicata e in fisica matematica. Il campo di applicazione dei metodi di trattamento delle equazioni alle derivate parziali si estende ora a numerose discipline scientifiche (biologia, ingegneria chimica, ingegneria meccanica, ma anche demografia, finanza ecc.). Alcuni progressi recenti hanno permesso di rispondere a domande rimaste a lungo senza risposta: se ne richiamano qui alcuni, nella descrizione di ricerche che riguardano la modellizzazione tramite equazioni alle derivate parziali.

I fenomeni il cui modello è definito attraverso equazioni alle derivate parziali (o sistemi di tali equazioni) sono quelli che possono essere descritti da funzioni di più variabili. Queste variabili possono essere spaziali, come nel caso dell’equazione verificata dal potenziale elettrostatico V(x, y, z), dove x, y, z sono le tre coordinate nello spazio tridimensionale, e possono essere spaziotemporali, come nell’equazione verificata dalla temperatura T(t, x, y, z) di un corpo solido (t designa allora il tempo). Più raramente, le variabili rappresentano quantità più astratte. Così, è di interesse considerare la densità nello spazio delle fasi di un gas rarefatto f(t, x, y, z, v_x, v_y, v_z ) dove v_x, v_y, v_z sono le componenti della velocità tridimensionale delle molecole del gas. Un altro esempio, usato in demografia, è la densità di individui f(t, a) che al tempo t hanno l’età a.

Molte equazioni alle derivate parziali sono basate sul seguente principio di modellizzazione: se ϱ(t, x, y, z) rappresenta la densità all’istante t e nel punto x, y, z di una quantità, j(t, x, y, z)=(j₁(t, x, y, z), j₂(t, x, y, z), j₃(t, x, y, z)) il flusso (vettoriale) di questa quantità e S(t, x, y, z) una sorgente (positiva o negativa) della quantità considerata, allora ϱ, j e S sono legate dalla seguente relazione:

Questa relazione è semplicemente la versione infinitesimale del principio che vuole che l’evoluzione di una quantità in un dominio dello spazio sia il risultato del bilancio della creazione/distruzione di tale quantità da una parte, e dell’ingresso/uscita nel dominio della stessa quantità dall’altra. Quando S(t, x, y, z)=0 e (per i=1, 2, 3) j_i(t, x, y, z)=ϱ(t, x, y, z)×u_i(t, x, y, z), dove u=(u₁, u₂, u₃) è un campo di velocità assegnato, si ottiene la seguente equazione, detta di trasporto:

Questa equazione è un modello di evoluzione della densità ϱ di una quantità (per es., la concentrazione di una specie chimica) in un campo di velocità assegnato (legato a uno scorrimento in meccanica dei fluidi). Si dice che essa è di ordine 1 perché vi compaiono unicamente derivate parziali di ordine 1.

Quando j₁, j₂e j₃ sono legate alla legge di Fick

dove κ è una costante, detta coefficiente di diffusione, si ottiene l’equazione di diffusione

Tale equazione rappresenta un modello della diffusione della densità ϱ di una quantità (per es., di nuovo, la concentrazione di una specie chimica) in un mezzo. Nel contesto della fisica statistica, tale diffusione proviene dal movimento erratico delle molecole sulla scala microscopica (moto Browniano). I sistemi che combinano i due precedenti tipi di equazioni e varie sorgenti (che possono dipendere dalle incognite) compaiono regolarmente e vengono sempre più utilizzati in fisica e in ingegneria. Tra i più importanti, si possono citare: 1) le equazioni di Eulero e di Navier-Stokes per la meccanica dei fluidi; in una delle versioni più semplici di questi sistemi (equazioni di Eulero per gas compressibili isoentropici), si ha (in notazione vettoriale, per i=1, 2, 3):

dove p(ϱ) è la legge di pressione, che si suppone nota, del gas (funzione della densità, a entropia fissata) e le incognite sono la densità ϱ(t, x, y, z) e la velocità tridimensionale (u₁(t, x, y, z), u₂(t, x, y, z), u₃(t, x, y, z). Queste equazioni rappresentano il bilancio di massa e di quantità di moto in un fluido (non viscoso, compressibile e isoentropico); 2) i sistemi di reazione-diffusione, che giocano un ruolo dominante nella dinamica delle popolazioni con struttura spaziale. Un esempio tipico corrisponde all’evoluzione di una popolazione in un ambiente unidimensionale, tenendo conto della diffusione (e del suo coefficiente κ), del suo tasso di riproduzione r, e della capacità di carica C del mezzo. Si ha allora l’equazione di Fisher-KPP (Kolmogorov-Petrovsky-Piskounov):

dove ϱ(t, x, y) è la densità di individui. Il flusso di Ricci, che gioca un ruolo determinante nella soluzione della congettura di Poincaré (Perelman 2002, 2003a, 2003b), è legato a questo tipo di equazione; 3) le equazioni di Maxwell in elettromagnetismo, che reggono l’evoluzione dei campi elettrici e magnetici creati da cariche e correnti elettriche assegnate; 4) le equazioni dell’elasticità, che sono alla base dei calcoli in meccanica dei solidi.

Numerose combinazioni delle equazioni precedenti intervengono in ambiti complessi della fisica. Così, lo studio della combustione fa intervenire una combinazione delle equazioni della meccanica dei fluidi e della reazione-diffusione. Ugualmente, lo studio dei plasmi può fare intervenire una combinazione di equazioni della meccanica dei fluidi e delle equazioni di Maxwell.

Le equazioni alle derivate parziali sono raramente date nello spazio (o spazio-tempo) intero. Più spesso, sono assegnate su un intervallo di tempo (quando il tempo è una delle variabili) e in un dominio dello spazio (per es., un intervallo limitato quando la variabile spaziale è unidimensionale). È utile allora completarle con delle condizioni al contorno adatte. Tali condizioni al contorno sono vincoli verificati dalle incognite (o derivate di tali incognite) su tutta la o parte della frontiera del dominio spaziale nel qua le sono date le equazioni.

Studio qualitativo delle equazioni alle derivate parziali. – Lo studio qualitativo delle equazioni alle derivate parziali provenienti dalla modellistica ha conosciuto recentemente progressi molto importanti. Gli interrogativi che si pongono riguardano l’esistenza e l’unicità delle soluzioni, la stabilità di queste ultime rispetto al dato iniziale o ai parametri dell’equazione (stabilità strutturale), la regolarità delle soluzioni (ci si chiede, per es., quante volte le soluzioni sono derivabili), il comportamento asintotico delle soluzioni, cioè quando alcune delle variabili tendono a un limite. Uno dei casi più studiati riguarda l’andamento delle soluzioni quando il tempo tende all’infinito. Sviluppi recenti in questo ambito – teoria dell’ipocoercività (Villani 2009), dimostrazione rigorosa dello smorzamento di Landau nella teoria dei plasmi (Mouhot, Villani 2011) – hanno permesso di risolvere problemi antichi.

Tutte queste problematiche sono legate al concetto di stima a priori: si tratta di dimostrare che le eventuali soluzioni di un’equazione alle derivate parziali verificano alcune proprietà quantitative. Il termine a priori significa che si considerano soluzioni appunto eventuali, prima ancora di averne dimostrato l’esistenza. Così, le soluzioni dell’equazione di diffusione (per es., con condizioni al contorno di Neumann omogenee ∇ϱ(t, x, y, z)·n(x, y, z)=0, per t≥0 e (x, y, z)∈∂Ω) verificano la disequazione

quando t≥s. Tale stima a priori è chiamata principio del massimo. Allo stesso modo, le soluzioni dell’equazione di trasporto verificano, da parte loro, l’uguaglianza

per t≥s. Più in generale, bisogna notare che alcuni principi fisici (conservazione dell’energia, decrescenza dell’entropia) forniscono spesso tali stime a priori. Così, il principio del massimo precedentemente enunciato corrisponde, nel contesto dell’equazione di diffusione verificata dalla temperatura di un solido, alla proprietà di non crescita della temperatura massima di un corpo (termicamente isolato) nel tempo. Allo stesso modo, l’uguaglianza verificata da una soluzione dell’equazione di trasporto illustra la conservazione della massa totale.

Le proprietà qualitative più importanti delle equazioni alle derivate parziali sono quelle legate a un fenomeno osservato sperimentalmente. Tra queste, si possono citare: 1) la comparsa spontanea di singolarità. Infatti, anche quando la soluzione al tempo 0 di alcune equazioni è molto regolare (cioè quando la si può derivare un numero infinito di volte), può succedere che, a partire da un dato istante, tale soluzione presenti una singolarità, cioè essa non sia più derivabile, o persino non sia più continua. Così, il sistema di Eulero in meccanica dei fluidi può produrre tali singolarità (urti), legate al fenomeno fisico del ‘muro del suono’. In tali situazioni, che appaiono generalmente quando si considerano sistemi iperbolici di leggi di conservazione, le derivate che compaiono nell’equazione alle derivate parziali non possono essere definite nel modo tradizionale (poiché la soluzione non è più derivabile) e bisogna ricorrere a generalizzazioni legate alla teoria delle distribuzioni. Progressi recenti nello studio dei sistemi iperbolici sono stati ottenuti grazie ai metodi d’interazione di onde (Bianchini, Bressan 2005). 2) L’esistenza di onde progressive, ossia soluzioni particolari di equazioni alle derivate parziali che hanno una forma specifica: esse dipendono, per es., da x−ct, con c assegnato, quando si considera una classe di equazioni la cui incognita è una funzione del tempo t e di una variabile unidimensionale x. L’equazione di Fisher-KPP fornisce un bell’esempio di esistenza di tali onde progressive, che si ritrova nello studio sperimenta le delle invasioni di territorio da parte di una specie vivente.

In molti casi, si è condotti a considerare soluzioni la cui regolarità non permette di definire le derivate parziali in senso tradizionale. Si considera allora più spesso che le derivate siano definite nel senso delle distribuzioni, e si parla di soluzioni deboli. Tale nozione di soluzione è stata recentemente ancora più indebolita, cosa che ha condotto alla teoria delle soluzioni rinormalizzate (DiPerna, Lions 1989a), usate per la prima volta nell’ambito della classe di equazioni dette cinetiche, poi per altre classi di equazioni (ellittiche, paraboliche ecc.). Oltre alla rinormalizzazione, si introducono a volte misure di difetto, come nel caso dell’equazione di Landau per i plasmi. Il problema dell’unicità delle soluzioni deboli conduce spesso a difficoltà considerevoli, e talvolta viene risolto negativamente, come è dimostrato dagli sviluppi recenti in meccanica dei fluidi (De Lellis, Szekelyhidi 2009).

Soluzioni esplicite e approssimate. – La ricerca delle soluzioni esplicite o semiesplicite (per es., sotto forma di serie, o di integrale con parametri) ha svolto un importante ruolo storico nello studio delle equazioni alle derivate parziali provenienti dalla modellistica, e in particolare dalla modellizzazione dei fenomeni fisici. Due metodi di ricerca di tali soluzioni hanno un’importanza particolare: i metodi legati all’analisi di Fourier (serie e trasformata di Fourier), particolarmente adatti alle equazioni alle derivate parziali più semplici, quelle lineari a coefficienti costanti, come l’equazione di diffusione; il metodo delle caratteristiche, appropriato per le equazioni (e non per i sistemi) alle derivate parziali del primo ordine (che non fanno intervenire che derivate al più del primo ordine), lineari o meno, a coefficienti costanti o meno. Le caratteristiche sono curve nello spazio-tempo definite come soluzioni di un’equazione differenziale ordinaria (o di un sistema di tali equazioni), e sulle quali la soluzione dell’equazione alle derivate parziali ha un comportamento che può essere descritto in maniera semplice. Questa teoria ha avuto sviluppi teorici importanti in questi ultimi anni, nel caso in cui l’equazione alle derivate parziali del primo ordine considerata ha coefficienti poco regolari (DiPerna, Lions 1989b).

Anche se le soluzioni esplicite continuano ad avere molto interesse (in particolare per fornire soluzioni di riferimento nell’ambito del calcolo scientifico), una parte importante della ricerca sulle equazioni alle derivate parziali si è orientata verso il calcolo delle soluzioni approssimate basate su una discretizzazione delle equazioni, e sulla programmazione effettiva delle equazioni discretizzate. Lo studio della qualità della discretizzazione delle equazioni è l’oggetto dell’analisi numerica.

Analisi asintotica delle equazioni alle derivate parziali. – Un aspetto importante della modellizzazione tramite equazioni alle derivate parziali è l’analisi asintotica legata ai parametri che intervengono in tali equazioni. Quest’analisi comincia in generale con un’adimensionalizzazione delle equazioni: bisogna scegliere quantità caratteristiche degli oggetti studiati (una lunghezza tipica in uno scorrimento di fluidi, la velocità tipica dello stesso scorrimento ecc.), poi effettuare un cambiamento di variabili e di incognita, che fa emergere quantità senza dimensioni. Nel contesto della meccanica dei fluidi, il numero di Mach (rapporto tra la velocità di uno scorrimento e la velocità del suono) e il numero di Reynolds (rapporto tra il prodotto della velocità del fluido e una lunghezza caratteristica da un lato, e la viscosità del fluido dall’altro) sono delle quantità di questo tipo. Quando quantità di questo tipo sono (nell’ambito di un esperimento assegnato) molto piccole (le si indica allora con ε) o molto grandi (le si indica allora con 1/ε) rispetto a 1, si è tentati di effettuare nell’equazione il limite ε→0, e di vedere cosa ne è della soluzione dell’equazione. I casi più interessanti sono quelli nei quali questa soluzione converge verso la soluzione di un’altra equazione. Questa situazione compare in innumerevoli problemi provenienti dall’ingegneria, dalla fisica o da altre scienze naturali. La dimostrazione rigorosa del passaggio dalle soluzioni deboli (rinormalizzate) dell’equazione di Boltzmann alle soluzioni deboli dell’equazione di Navier-Stokes incompressibile costituisce uno sviluppo recente in tale direzione (Golse, Saint-Raymond 2004).

Tra i piccoli parametri adimensionali che intervengono spesso, possono essere citati: 1) il rapporto tra la velocità tipica di un fenomeno e la velocità della luce, associato al limite classico (non relativistico) di un sistema di equazioni; 2) il rapporto tra la costante di Planck e alcuni parametri che intervengono in un fenomeno fisico, associato al limite semiclassico (che permette il passaggio dalla meccanica quantistica alla meccanica classica) di un sistema di equazioni; 3) il numero di Mach precedentemente definito, associato al limite di fluido incompressibile; 4) il numero di Reynolds precedentemente definito, associato al limite di fluido non viscoso.

L’analisi asintotica può portare alla trasformazione di un sistema di equazioni in un altro sistema, che differisce dal primo nel fatto che le condizioni al contorno che gli sono associate sono diverse: per es., una delle condizioni iniziali associate al primo sistema può essere di troppo nel secondo. Compare allora una zona (tipicamente di grandezza ε nella variabile temporale) nella quale una delle incognite del sistema avrà una derivata temporale di ordine 1/ε: si parla dunque di strato limite (talvolta detto strato iniziale, quando è il dato iniziale cui si fa riferimento).

Bibliografia: R.J. DiPerna, P.L. Lions, On the Cauchy problem for Boltzmann equations: global existence and weak stability, «Annals of mathematics», 1989a, 130, pp. 321-66; R.J. Di-Perna, P.L. Lions, Ordinary differential equations, transport theory and Sobolev spaces, «Inventiones mathematicae», 1989b, 98, pp. 511-47; G. Perelman, The entropy formula for the Ricci flow and its geometric applications, 2002, http://arxiv.org/pdf/math/0211159.pdf; G. Perelman, Finite extinction time for the solutions to the Ricci flow on certain three-manifolds, 2003a, http://arxiv.org/pdf/math/0307245.pdf; G. Perelman, Ricci flow with surgery on three-manifolds, 2003b, http://arxiv.org/pdf/math/0303109.pdf; F. Golse, L. Saint-Raymond, The Navier-Stokes limit of the Boltzmann equation for bounded collision kernels, «Inventiones mathematicae», 2004, 155, 1, pp. 81-161; S. Bianchini, A. Bressan, Vanishing viscosity solutions of nonlinear hyperbolic systems, «Annals of mathematics», 2005, 161, 1, pp.223-342; C. De Lellis, L. Szekelyhidi, The Euler equations as a differential inclusion, «Annals of mathematics», 2009, 170, pp.1417-38; C. Mouhot, C. Villani, On Landau damping, «Acta mathematica», 2011, 207, 1, pp. 29-201; C. Villani, Hypocoercivity, «Memoirs of the American mathematical society», 2009,202, 950.