Klein, modello di
Klein, modello di
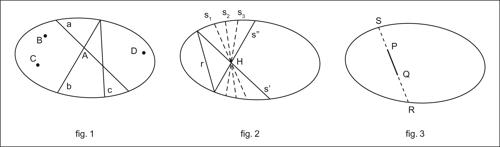
Klein, modello di modello coerente di geometria non euclidea di tipo iperbolico in ambiente euclideo. I punti del piano iperbolico sono rappresentati dai punti interni a una conica e le rette sono le corde della conica, considerate come segmenti aperti, cioè privi degli estremi sulla conica. In questo modello risultano verificati tutti gli assiomi di incidenza e di ordinamento, oltre all’assioma della continuità. Si ha infatti, che: due rette distinte o hanno un solo punto comune oppure sono prive di punti comuni; per un punto passano infinite rette (perché per un punto interno alla conica passano infinite corde). Inoltre, per un punto non appartenente a una retta passano almeno due (di fatto infinite) parallele alla retta. È infatti possibile, come appare nella figura 2, data una corda r, condurre da un punto H non appartenente a r, infinite corde che non intersecano internamente r.
Per verificare gli assiomi di congruenza è necessario definire una distanza tra due punti qualsiasi P e Q. Indicati con S e R i punti della conica allineati con P e Q (figura 3) si dà la seguente definizione:
La distanza d, definita mediante il logaritmo naturale del birapporto dei punti S, P, Q, R, soddisfa gli assiomi della distanza. Con tale definizione, ogni retta (una corda cioè che abbia come estremi “infiniti” due punti della conica come S e R) ha una lunghezza infinita e, a parte le proprietà di parallelismo, si comporta in tutto e per tutto come una retta euclidea.