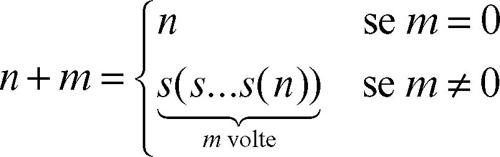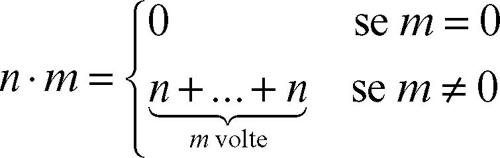N

N

N (insieme dei numeri naturali) insieme numerico {0, 1, 2, 3, ...}, indicato con il simbolo N, la cui origine è nell’operazione intuitiva del contare. La nozione di numero naturale è presente già nelle manifestazioni più arcaiche del pensiero matematico ed è alla base di tutto l’edificio matematico: è molto esplicativa, in questo senso, la frase del matematico tedesco L. Kronecker, il quale disse «Dio ha creato i numeri naturali; tutto il resto è opera dell’uomo». Nonostante la sua intuitività e immediatezza, una definizione formale rigorosa di insieme dei numeri naturali fu data solamente nel 1889 dal matematico italiano G. Peano; tale definizione individua cinque assiomi (detti assiomi di → Peano o assiomi dei numeri naturali) per N, i quali assumono come nozioni primitive quelle di «numero naturale», di «zero» e di «successore di un numero naturale»:

a) zero è un numero naturale;

b) se n è un numero naturale, anche il successore di n è un numero naturale;

c) se i successori di due numeri naturali sono uguali, allora anche i due numeri naturali sono uguali;

d) zero non è successore di alcun numero naturale;

e) se A è un insieme di numeri naturali che contiene lo zero e il successore di ogni numero appartenente a esso, allora A coincide con tutto l’insieme dei numeri naturali.

L’ultimo assioma è noto come principio di induzione matematica e può essere riformulato in modo equivalente come segue:

f) sia P una proprietà concernente i numeri naturali che è soddisfatta da zero e che, se soddisfatta da un dato numero naturale, è soddisfatta anche dal suo successore. Allora P è soddisfatta da ogni numero naturale.

Gli assiomi di Peano permettono di costruire l’aritmetica come sistema ipotetico-deduttivo: essi possono in effetti essere usati per dare una definizione formale di insieme dei numeri naturali nell’ambito della teoria degli insiemi. Formalmente, è possibile pertanto definire l’insieme dei numeri naturali come una qualsiasi terna (N, 0, s), dove N è un insieme non vuoto, 0 è un elemento di N (detto zero) e s: N → N è un’applicazione che soddisfa i seguenti assiomi (che sono una riformulazione dei cinque assiomi di Peano):

a) s è un’applicazione iniettiva;

b) 0 non appartiene all’immagine di s;

c) se A ⊆ N è un sottoinsieme contenente 0 tale che ∀x ∈ A, s(x) ∈ A, allora A = N.

L’applicazione s è detta applicazione del successore e si pone s(0) = 1, s(1) = 2, s(2) = 3 ecc., dove le uguaglianze vanno intese come definizioni. In altre parole, una volta dato l’elemento 0 e l’applicazione del successore s, è possibile definire, mediante un opportuno numero di iterazioni dell’applicazione s, ogni numero naturale: il numero di iterazioni dell’applicazione del successore per ottenere un dato numero ne costituirà la definizione stessa. Una tale terna (N, 0, s) è indicata semplicemente con il simbolo N, sottintendendo l’esistenza di 0 e di s. È bene osservare che l’esistenza di una tale terna non è dimostrabile: essa è posta come assioma, detto assioma dell’infinito, ed è inserito tra gli assiomi della teoria degli insiemi di Zermelo-Fraenkel (→ Zermelo-Fraenkel, teoria di). Si può invece dimostrare che, se una tale terna esiste, allora essa è unica (a meno di isomorfismo).

Sull’insieme N dei numeri naturali si definiscono in modo assiomatico due operazioni: l’operazione di addizione tra due numeri naturali, indicata con il simbolo +, ponendo, per ogni coppia n, m di numeri naturali,

In particolare, si ritrova l’uguaglianza s(n) = n + 1, che spiega il nome dell’applicazione s. L’operazione binaria di addizione +: N × N → N soddisfa la proprietà associativa e la proprietà commutativa e ammette 0 come elemento neutro. Dotato di tale operazione, l’insieme N dei numeri naturali acquisisce pertanto la struttura algebrica di monoide commutativo. Una seconda operazione definita in N è quella di moltiplicazione, indicata con il simbolo × o più semplicemente ⋅: essa è definita ponendo per ogni coppia n, m di numeri naturali

Dotato di tale operazione, che gode della proprietà associativa e di quella commutativa, N acquisisce la struttura algebrica di semigruppo commutativo. Come operazione su N la moltiplicazione ammette come elemento neutro 1. Pertanto, dotato dell’operazione di moltiplicazione, N₀ acquisisce la struttura algebrica di monoide commutativo ed è detto il monoide moltiplicativo di N. La moltiplicazione definita su N è inoltre compatibile con l’operazione di addizione sopra definita, nel senso che valgono le proprietà distributive.

L’insieme N è dotato in modo naturale di una relazione d’ordine stretto, indicata con il simbolo < e definita come segue: se n e m sono due numeri naturali, allora n < m se e solo se m segue n, vale a dire se m = s(... s(n)), per un opportuno numero di iterazioni dell’applicazione s. Un numero n è detto positivo se soddisfa la disuguaglianza 0 < n. La relazione d’ordine stretto < definisce una relazione d’ordine totale, indicata con il simbolo ≤, definita da n ≤ m se e solo se n = m oppure n < m. Tale relazione d’ordine è compatibile con la struttura algebrica di cui è dotato N, nel senso che valgono le due seguenti proprietà, dove a, b e c sono arbitrari numeri naturali:

• se a ≤ b allora a + c ≤ b + c

(compatibilità con l’addizione)

• se a ≤ b allora a ⋅ c ≤ b ⋅ c

(compatibilità con la moltiplicazione)

Oltre a essere totalmente ordinato, dotato della relazione ≤, l’insieme N è ben ordinato (vale a dire che ogni suo sottoinsieme non vuoto ammette minimo) e archimedeo (vale a dire che se a e b sono due numeri naturali con a ≠ 0 allora esiste un numero naturale n tale che b < na; si veda → Archimede, assioma di).

Sull’insieme N dei numeri naturali può essere definita una terza operazione, rispetto alla quale però esso non è chiuso: essa è l’operazione di sottrazione, indicata con il simbolo – e operazione inversa dell’addizione. Dati due naturali a e b, si definisce a – b come quel numero naturale c, se esiste, per cui è soddisfatta l’equazione b + c = a. Se tale equazione ammette soluzione, allora l’ammette unica; d’altra parte, una soluzione è definita, nell’ambito dei numeri naturali, se e solo se b ≤ a. La non chiusura di N rispetto all’operazione di sottrazione equivale al fatto che il monoide (N, +) non è un gruppo: nessun numero naturale diverso da zero (il quale è inverso di sé stesso) ammette inverso rispetto a +. Per ottenere tali elementi è necessario effettuare un ampliamento di N: tale idea è alla base della definizione dell’insieme Z dei numeri interi, che coincide con la chiusura di N rispetto all’operazione di sottrazione.

Per le diverse accezioni del concetto di numero naturale a seconda dei contesti di utilizzo, si vedano anche le voci → numero cardinale; → numero ordinale.