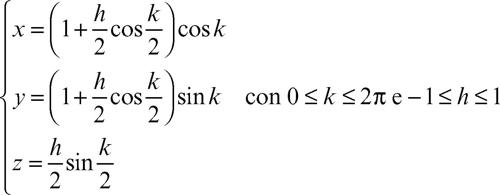Mobius, nastro di
Mobius, nastro di
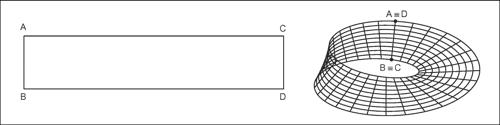
Möbius, nastro di superficie rigata non orientabile, con una sola faccia e un solo bordo e, pertanto, con caratteristica di Eulero nulla (→ Eulero, relazione di). Il nastro di Möbius può essere ottenuto a partire da un foglio rettangolare ABCD: si effettua una torsione di 180° del lato AB e lo si porta a coincidere con il lato CD, in modo tale che il punto A si identifichi con il punto D e il punto B con il punto C. Come superficie di R3 può essere rappresentato dalle seguenti equazioni parametriche:
Il nastro così descritto ha larghezza 1. Variando il parametro k ci si muove lungo il nastro, mentre variando il parametro h si parte dal bordo, ci si allontana e si torna al bordo.
Tale superficie gode di notevoli proprietà topologiche: a differenza delle superfici ordinarie che hanno sempre due facce, per cui è possibile fare un percorso ideale su una di esse senza mai passare all’altra faccia, la superficie del nastro di Möbius può essere percorsa totalmente con continuità sia sulla faccia “esterna” sia su quella “interna” senza attraversare né il bordo né la superficie. Se si traccia con una punta scrivente una linea media lungo tutto il nastro partendo da un punto casuale, si nota che la traccia si snoda sull’intera superficie del nastro, che è quindi unica; si ritorna al punto di partenza, ma dalla parte opposta della striscia, e solo dopo aver percorso due giri ci si ritrova sul lato iniziale. Tagliando il nastro a metà, lungo una parallela al bordo, si ottiene un altro nastro, ma con una torsione doppia (360°) costituito da una superficie doppia, cioè orientabile, dotata di due bordi. Il nastro di Möbius viene associato alla bottiglia di → Klein, dalla quale può essere ottenuto tagliandola opportunamente.