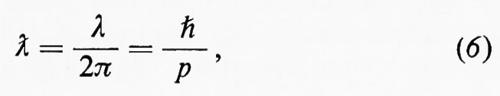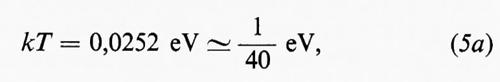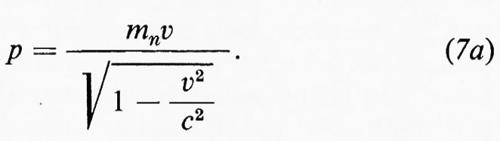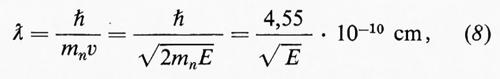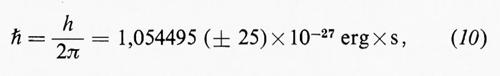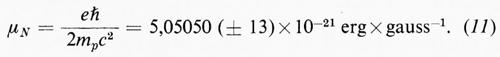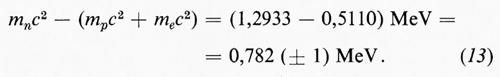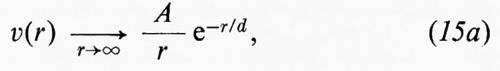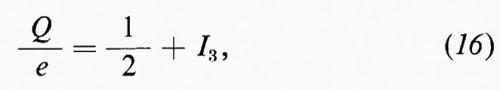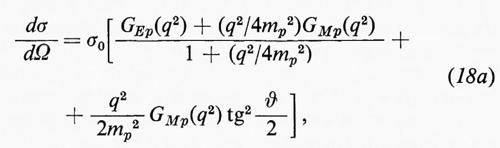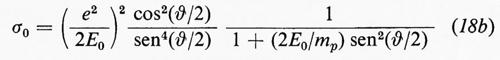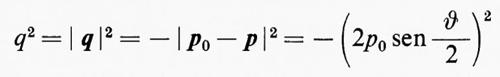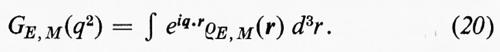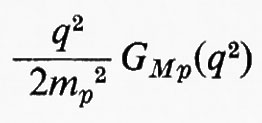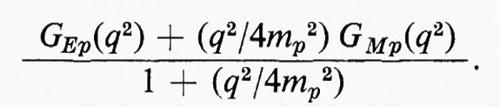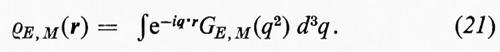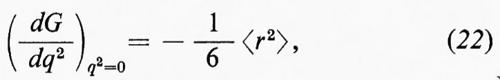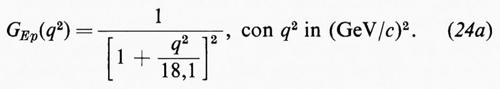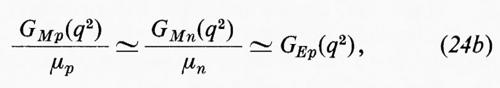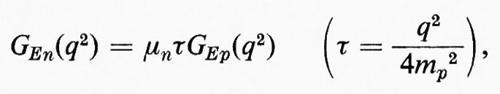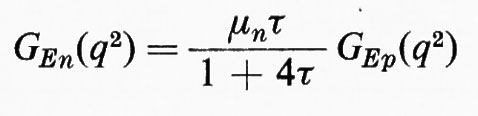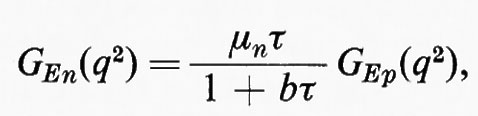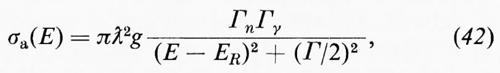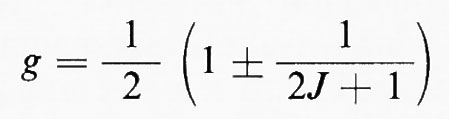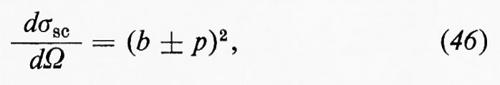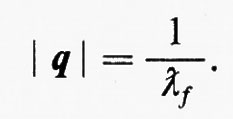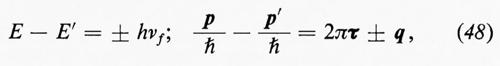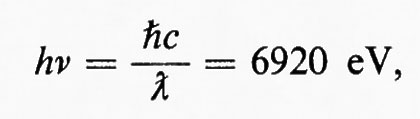Neutroni

Neutroni

di Edoardo Amaldi

SOMMARIO: 1. Il neutrone. □ 2. La scoperta del neutrone e della radioattività artificiale. □ 3. I neutroni lenti. □ 4. Le principali proprietà del neutrone. □ 5. I diversi tipi d'interazione del neutrone con le altre particelle. □ 6. La struttura elettromagnetica del neutrone. □ 7. Le sorgenti di neutroni. □ 8. Le reazioni prodotte da neutroni. □ 9. La rivelazione dei neutroni. □ 10. Cenno ad alcuni impieghi dei neutroni. □ Bibliografia.

1. Il neutrone.

Il neutrone è una particella elettricamente neutra di dimensioni subatomiche (~10^-13 cm) e di massa poco superiore a quella del protone (~10^-24 g). Insieme al protone esso è uno dei costituenti del nucleo atomico dal quale viene emesso in molte reazioni nucleari. A sua volta il neutrone, usato come proiettile per bombardare il nucleo dei diversi elementi chimici, dà luogo a numerosissime reazioni nucleari, in molte delle quali si producono nuovi isotopi radioattivi di tutti gli elementi chimici. Lo studio approfondito di queste reazioni nucleari e dei loro prodotti ha permesso e permette ancor oggi di allargare enormemente le nostre conoscenze sulla struttura dei nuclei e sui loro processi di disintegrazione spontanea.

Gli isotopi radioattivi così prodotti trovano poi i più diversi impieghi, fra i quali basti ricordare l'uso di molti di essi come traccianti per lo studio di processi chimici, biologici e industriali, di altri come sorgenti di energia di caratteristiche insostituibili e di altri ancora per scopi radiografici e terapeutici.

Il neutrone, purché di energia sufficientemente bassa, costituisce una sonda, unica e insostituibile, per l'esplorazione di certe proprietà della materia allo stato solido, liquido o gassoso. Esso inoltre è l'agente che inizia e mantiene le reazioni nucleari a catena utilizzate nei reattori nucleari, destinati alla ricerca o alla produzione di energia su scala industriale, e negli esplosivi nucleari.

Il neutrone è uno di quei corpuscoli di dimensioni subatomiche che nella terminologia attuale sono indicati complessivamente con il nome di ‛particelle elementari', anche se esse non mostrano affatto quella semplicità di struttura che è implicitamente suggerita dall'aggettivo ‛elementare'; questa qualifica è un residuo della terminologia usata all'epoca in cui l'esperienza non aveva ancora rivelato la complessità della loro struttura.

Infine, si ritiene che le stelle pulsanti o ‛pulsar' (v. stelle pulsanti) siano stelle ruotanti di neutroni, ossia stelle di raggio molto piccolo (dell'ordine di 10÷30 km), di massa dell'ordine di quella del Sole, nel cui interno la densità varia fra 10⁷ e 10¹⁴ g/cm³. Si pensa che tali stelle siano costituite prevalentemente da neutroni, essendo questa la sola forma stabile della materia in quelle particolari condizioni di densità e temperatura (T~10⁸ °K), e rappresentino il risultato del collasso gravitazionale subito da corpi celesti di massa inferiore a tre o quattro masse solari.

2. La scoperta del neutrone e della radioattività artificiale.

La scoperta del neutrone ebbe origine da alcune classiche esperienze di W. Bothe e H. Becker, i quali, nel 1930 a Charlottenburg, osservarono una ‛radiazione secondaria penetrante' emessa da vari elementi leggeri (litio, berillio, boro, fluoro) bombardati con le particelle alfa di un corpo radioattivo naturale (polonio) e la interpretarono come costituita da raggi gamma duri, ossia molto penetranti, in quanto dotati di energia considerata a quell'epoca come elevata: qualche MeV (1 MeV=10⁶ eV, 1 eV=1,6021×10^-12 erg). Lo studio di questa radiazione fu ripreso da I. Curie e Fr. Joliot, i quali, a Parigi nel 1932, scoprirono che essa può trasferire energie assai elevate (~5 MeV) ai protoni, o nuclei dell'atomo di idrogeno, presenti in straterelli sottili di sostanze idrogenate (come il cellofan, l'acqua, ecc.) esposti a detta radiazione. L'interpretazione di questo risultato, data dai due studiosi francesi ancora in termini di raggi gamma duri, dava luogo tuttavia a notevoli difficoltà, in quanto non si conosceva, né si conosce oggi, alcun processo capace di trasferire energie così elevate, e così frequentemente come veniva osservato, da uno dei fotoni costituenti i raggi gamma incidenti a un corpuscolo pesante come il protone.

Queste difficoltà divennero insormontabili quando, poco dopo, J. Chadwick, a Cambridge, in Inghilterra, dimostrò sperimentalmente che la radiazione penetrante in studio era capace di trasferire energie dello stesso ordine di grandezza anche ai nuclei di altri elementi leggeri, come Li, Be, B, ecc., fino a quello dell'N (azoto), il quale è dotato di massa circa 14 volte più grande di quella del protone. Chadwick si rese tuttavia subito conto che tutti i fenomeni fino ad allora osservati potevano essere pienamente spiegati se si faceva l'ipotesi che la radiazione penetrante, originariamente osservata da Bothe e Becker, fosse costituita, almeno in parte, da un nuovo tipo di corpuscoli elettricamente neutri e dotati di una massa molto prossima a quella del protone. I risultati delle sue esperienze insieme a questa interpretazione furono pubblicati da Chadwick in una lettera al direttore del giornale scientifico ‟Nature" di Londra il 17 febbraio 1932, lettera che, giustamente, è considerata come l'atto di nascita del neutrone (v. Amaldi, 1959; v. Beckurts e Wirtz, 1964).

Da queste prime esperienze e da altre eseguite poco dopo dagli stessi e da altri ricercatori fu possibile stabilire che la massa del nuovo corpuscolo, il neutrone, era di assai poco superiore a quella del protone (v. tab. I). Il fatto poi che i neutroni venissero emessi dai nuclei degli elementi leggeri sotto l'azione di particelle alfa suggeriva un nuovo modello di nucleo.

Prima della scoperta del neutrone si pensava infatti che i nuclei di tutti gli atomi consistessero in aggregati dei due corpuscoli elementari allora noti, protoni ed elettroni, in numero tale da dar luogo, nel loro insieme, a un sistema dotato del giusto valore della carica elettrica e della massa. Ma con l'avvento della meccanica quantistica, pochi anni prima, questo modello era diventato inaccettabile: come conseguenza del principio d'indeterminazione, un elettrone confinato entro le dimensioni di un nucleo (~10^-12 cm) doveva essere dotato di una quantità di moto e quindi anche di un'energia cinetica così elevate da essere incompatibili con quanto si sapeva già allora sulle energie in gioco nei nuclei.

La scoperta del neutrone apriva una via d'uscita da questa difficoltà. Diventava infatti plausibile l'ipotesi che non vi fossero elettroni nel nucleo, il quale risultava così costituito solo di protoni e di neutroni. La difficoltà sopra accennata nel caso degli elettroni non esiste nel caso dei protoni e dei neutroni; a causa della loro massa, che è circa 2.000 volte maggiore di quella degli elettroni, il limite inferiore che si deduce dal principio d'indeterminazione per la loro energia cinetica è pienamente compatibile con le energie in gioco nei nuclei.

Nasceva così un nuovo modello di nucleo costituito solo di protoni e neutroni (F. Perrin, W. Heisenberg, D. Iwanenko, 1932) ampiamente confermato da tutte le esperienze successive. In questo modello ogni nuclide è individuato da due numeri: il numero Z di protoni e il numero N di neutroni che lo costituiscono. La sua carica elettrica è pari a Ze, dove

e=4,80298 (±1)×10^-10 u.e.s.

=1,60210 (±6)×10^-19 coulomb (1)

è la carica elementare posseduta, con segno opposto, dal protone e dall'elettrone (l'errore sul valore della carica elettrica, riportato tra parentesi, si intende riferito all'ultima cifra significativa riportata), e la sua massa M (in unità di massa atomica) è sempre molto prossima al cosiddetto numero di massa

A=Z+N. (2)

Spesso, per individuare un nuclide, invece di dare i due numeri interi Z ed N, si assegnano i numeri interi A e Z. Così, per esempio, quando si scrive ²₁7₃Al s'intende un nuclide composto di Z=13 protoni ed N=A−Z=27−13=14 neutroni. Il numero Z, in questo caso 13, è detto numero atomico, in quanto è caratteristico dell'elemento chimico cui appartiene il nuclide considerato, in questo caso l'alluminio. Con queste convenzioni, il neutrone viene indicato con il simbolo 0¹n e il protone con l'uno o l'altro dei due simboli ¹₁p oppure 1¹H.

Due scoperte, strettamente legate fra loro, diedero nel 1934 un impulso straordinario allo studio delle reazioni nucleari e delle proprietà dei neutroni. Nel gennaio di quell'anno I. Curie e Fr. Joliot scoprirono che alcuni elementi leggeri, in particolare il B e l'Al, bombardati con le particelle alfa del Po, davano origine a corpi radioattivi non esistenti in natura, che emettevano elettroni positivi. Un esempio di questo nuovo fenomeno, comunemente indicato come ‛radioattività artificiale per bombardamento di particelle alfa', si ha nel seguente processo osservato dai ricercatori francesi nell'alluminio

²₁7₃Al+4₂He→³₁0₅P+¹₀n.

Il nuclide prodotto ³₁0₅P non esiste in natura, in quanto è instabile: esso decade spontaneamente, con una vita media di circa 3 minuti, emettendo un elettrone positivo e trasformandosi così in un nuclide di silicio secondo il processo

³₁0₅P→³₁0₄Si+e⁺+ν_e, (3)

dove ν_e indica il neutrino.

Dopo la scoperta dei Joliot-Curie era molto naturale pensare di produrre nuovi nuclidi radioattivi usando come proiettili incidenti particelle diverse dalle particelle alfa, come per esempio protoni o deutoni; esperimenti di questo tipo furono eseguiti qualche tempo dopo e diedero risultato positivo.

Più interessante per le sue conseguenze, in gran parte imprevedibili a quell'epoca, fu il tentativo di Fermi a Roma; egli pensò di poter osservare almeno qualche esempio di radioattività artificiale usando come proiettili i neutroni, nonostante che questi, essendo corpuscoli prodotti in reazioni nucleari iniziate da particelle alfa, fossero allora disponibili solo con intensità sempre molto deboli, dell'ordine di 10⁴÷10⁵ volte minori delle intensità delle sorgenti di particelle alfa usate dai Joliot-Curie. Fermi partiva dall'idea che l'assenza di carica elettrica del neutrone, grazie alla quale esso non perde energia per ionizzazione nell'attraversare la materia e non è respinto dal nucleo quando passa nelle sue vicinanze, potesse più che compensarne la bassa intensità.

La scoperta della radioattività artificiale per bombardamento di neutroni, fatta da Fermi nel marzo 1934, risultò particolarmente interessante non solo di per sé, ma anche per la varietà e l'importanza dei fenomeni scoperti nello studio sistematico eseguito in vari centri di ricerca e in particolare a Roma da Fermi e collaboratori (E. Amaldi, O. D'Agostino, F. Rasetti ed E. Segrè; v. Fermi, 1962).

Non è qui possibile ricapitolare, neppure per sommi capi, il succedersi dei nuovi fenomeni osservati e lo sviluppo storico della loro interpretazione. Basti ricordare che, già nel corso del 1934, fu dimostrato che i neutroni possono produrre processi di diverso tipo indicati con i simboli (n, α), (n, p) ed (n, γ), dove la prima e la seconda lettera fra parentesi rappresentano rispettivamente la particella incidente e la particella emessa. Fu anche dimostrato, a Roma, che l'ultimo dei suddetti processi, chiamato spesso cattura radiativa del neutrone; può essere prodotto in tutti gli elementi chimici, dai più leggeri fino ai più pesanti, come il tono e l'uranio. Negli anni successivi, in diversi laboratori, furono scoperti molti altri tipi di reazioni nucleari provocate da neutroni, come per esempio i processi (n, 2n), (n, 3n), (n, pn), (n, d), ecc. Particolarmente importante fu la scoperta fatta nel 1939 a Berlino da O. Hahn e F. Strassmann, i quali dimostrarono che sotto l'azione dei neutroni gli elementi più pesanti, come il torio e l'uranio, subiscono il fenomeno della scissione, o fissione, che sta alla base delle reazioni a catena oggi correntemente usate nei reattori nucleari.

3. I neutroni lenti.

Per poter comprendere la straordinaria varietà di esperienze che furono fatte allora e che vengono fatte ancor oggi con i neutroni, è però necessario tornare per un momento al 1934. Nel tentativo di stabilire una scala empirica delle attività prodotte nei vari elementi quando venivano irraggiati con neutroni in condizioni ben definite, Fermi, Amaldi, Pontecorvo, Rasetti e Segrè scoprirono, nell'ottobre di quell'anno, che la produzione di nuclidi radioattivi attraverso le reazioni (n, γ) veniva aumentata di un fattore dell'ordine di 20÷50, talvolta anche 100, se la sorgente di neutroni e il materiale irraggiato venivano circondati con sostanze idrogenate come l'acqua o la paraffina (v. Fermi, 1962).

Questo effetto era chiaramente molto interessante non solo dal punto di vista pratico, in quanto forniva un metodo molto semplice per aumentare di un grosso fattore la produzione di molte reazioni nucleari, ma anche, e soprattutto, per le varie implicazioni che la sua interpretazione comportava e perché, come si dirà nel seguito, apriva la via a una vasta serie di nuovi fenomeni.

Fermi si rese subito conto che l'effetto delle sostanze idrogenate poteva essere spiegato se si facevano le due seguenti ipotesi: a) nell'acqua o nella paraffina l'energia dei neutroni può venir enormemente ridotta in seguito a un numero grande, ma non grandissimo, di urti elastici successivi contro i protoni; b) i neutroni così rallentati, indicati fin d'allora come ‛neutroni lenti', sono molto più efficaci dei neutroni veloci nel produrre certe reazioni nucleari, in particolare le reazioni (n, γ).

Queste due ipotesi furono confermate pienamente in seguito a numerose esperienze eseguite dal gruppo di Roma, come anche da altri gruppi, tanto che in breve tempo furono considerate non più come ipotesi, ma come fatti bene accertati. Fu anche dimostrato, già dall'autunno 1934, che la proprietà a) non è esclusiva delle sostanze idrogenate, ma è comune a tutte le sostanze che assorbono molto poco i neutroni e contengono un'alta percentuale di elementi leggeri. Inoltre, esperienze eseguite in vari laboratori nel corso del 1935 permisero di stabilire che nel processo di rallentamento l'energia dei neutroni si degrada fino a ridursi al livello energetico che è proprio dell'agitazione termica delle molecole. Da questo momento in poi essi non possono più seguitare a perdere energia, ma si muovono, attraverso il materiale usato per il loro rallentamento, con l'energia propria dell'agitazione termica; il loro moto è simile a quello delle molecole di un gas rarefatto che diffonda entro un materiale spugnoso. Questo processo, che è prima di rallentamento e poi di diffusione termica, viene sempre interrotto o perché il neutrone sfugge dalla superficie del materiale rallentante o perché esso viene catturato da uno dei nuclei presenti.

Alcuni anni dopo fu introdotto il termine ‛moderatore' per indicare qualunque materiale che si presti a provocare il rallentamento dei neutroni e a mantenere successivamente, per un tempo abbastanza lungo, il processo di diffusione termica. Le proprietà dei diversi moderatori e il meccanismo di rallentamento e di diffusione dei neutroni sono stati oggetto, dal 1935 a oggi, di uno studio approfondito, anche per l'interesse che questi problemi presentano per la progettazione e la costruzione dei reattori.

Nello studio di questi fenomeni conviene distinguere tre intervalli di energia: il primo si estende dall'energia iniziale E₀ con cui i neutroni vengono emessi dalla sorgente, dell'ordine di qualche MeV o superiore, fino a circa 1 eV. In questa regione, detta ‛regione epitermica', nell'urto elastico neutrone-nucleo gli atomi del moderatore si possono considerare liberi. Ma, per energie inferiori a 1 eV, il fatto che gli atomi urtati siano legati chimicamente nelle molecole o nei cristalli del moderatore non può più essere trascurato, in quanto determina un cambiamento della sezione d'urto elastico osservata (Amaldi e Fermi, 1936); in particolare, il processo di rallentamento seguita ad aver luogo ma è meno efficace, nel senso che la frazione di energia persa in media per ogni urto è minore che per i neutroni al di sopra di 1 eV. Questa è solo una delle conseguenze del fatto che, affinché un urto sia rallentante, è necessario che con esso si ecciti uno dei moti oscillatori o rotatori delle molecole o dei cristalli presenti (Fermi, 1936). Dopo aver attraversato questa regione, detta spesso ‛regione chimica', il neutrone raggiunge la ‛regione termica', in cui negli urti successivi esso talvolta cede, talaltra riceve energia dagli oscillatori e dai rotatori del moderatore. Il processo di rallentamento attraverso la regione chimica fino al raggiungimento dell'energia termica viene indicato nella letteratura come processo di ‛termalizzazione dei neutroni' (v. Egelstaff e Poole, 1969).

Il problema matematico del rallentamento dei neutroni dall'energia iniziale fino alla regione chimica e della loro successiva termalizzazione, impostato nella sua generalità, è assai complicato, in quanto comporta la risoluzione di un'equazione integrodifferenziale, detta ‛del trasporto', in cui figura come incognita la densità n(E, W, r, t), all'istante t nel punto r del moderatore, dei neutroni dotati di energia E e con velocità nella direzione W. Sono stati tuttavia sviluppati dei metodi di calcolo approssimati che permettono di risolvere il problema con un'accuratezza sufficiente per la maggior parte degli scopi. Fra questi metodi approssimati va ricordata la ‛teoria dell'età' di Fermi, iniziata fin dal 1936 e sviluppata da Fermi stesso più tardi anche nei particolari. Essa si caratterizza per la sua semplicità ed eleganza, anche se in molti casi fornisce soluzioni non sufficientemente accurate (v. Fermi, 1965).

Un problema molto più semplice di quello sopra enunciato s'incontra se, in condizioni di stazionarietà, ossia con sorgenti di neutroni costanti nel tempo e moderatori fermi, le cose sono disposte in modo tale che n(E, W, r) sia praticamente indipendente da r entro una regione spaziale abbastanza estesa. In queste condizioni la densità n(E, W, r) si riduce a una semplice funzione dell'energia E dei neutroni, legata al flusso di neutroni ϕ(E), ossia al numero di neutroni che passa attraverso l'unità di superficie nell'unità di tempo, dalla relazione:

ϕ(E) dE=n(E)v dE. (4)

Le condizioni sopra descritte si realizzano sperimentalmente in maniera abbastanza facile; in particolare, esse sono praticamente sempre rispettate nella zona centrale di un reattore di ricerca, ove, come si dice, il flusso dei neutroni lenti è ‛piatto'.

La fig. 1 mostra i risultati sperimentali ottenuti da Beyster e collaboratori (1952) per il flusso dei neutroni rallentati in soluzioni di acido borico in acqua a diverse concentrazioni; essi sono confrontati con i calcoli eseguiti da vari autori (H. Amster, 1957; M. Nelkin, 1960) che hanno adottato diverse schematizzazioni per i livelli energetici di traslazione, rotazione e vibrazione della molecola d'acqua nel processo di termalizzazione. Delle tre curve una si riferisce all'acqua pura mentre le altre due ad acqua ‛avvelenata' con boro, il cui isotopo ¹⁰B ha un'elevata sezione d'urto di cattura per neutroni lenti (v. sotto, cap. 8, in particolare l'equazione 33c).

Qui basta far notare l'andamento di ϕ(E) al di sopra di 1 eV, che, secondo una formula dimostrata da Fermi nel 1936, segue la legge E^-1. Al di sotto di 1 eV inizia la zona chimica e a energie ancora più basse lo spettro diventa di tipo maxwelliano, distorto per la presenza di nuclei (come quelli di idrogeno e di boro) che assorbono secondo la legge v^-1 e che pertanto impoveriscono lo spettro nella parte delle bassissime energie.

Come si vede dalla fig. 1, facendo uso di una sorgente che emette nucleoni di energia eguale o superiore a qualche MeV, contornata da un moderatore, lo sperimentatore può disporre di neutroni dotati di uno spettro continuo di energia che si estende da E₀ fino a energie eguali o inferiori a kT. A temperatura ambiente (20 °C) si ha

che, eguagliato all'energia cinetica di un neutrone, ½mv0²=kT, dà:

v₀=2.198 m/s. (5b)

Per molti problemi, la grandezza che caratterizza il comportamento del neutrone, più che l'energia cinetica o la velocità, è la lunghezza d'onda di de Broglie λ, legata alla quantità di moto p dalla ben nota relazione

dove

Per neutroni di velocità non molto elevata v≪c) l'espressione relativistica (7a) si riduce all'espressione classica

p≃m_nv (7b)

e la (6) diventa:

dove E è l'energia cinetica del neutrone espressa in eV.

Questa formula mette bene in evidenza le straordinarie possibilità che sono aperte allo sperimentatore che lavora con neutroni: per energie dell'ordine di 100 MeV, la lunghezza d'onda è dell'ordine di grandezza delle dimensioni delle particelle elementari, a 1 MeV è dell'ordine delle dimensioni di un nucleo, a 10^-3÷10^-4 eV essa è dell'ordine delle dimensioni atomiche (v. Hughes, 1959; v. Shull e Wollan, 1956). Raffreddando il moderatore a temperature molto basse e facendo uso di opportuni monocromatori o selettori di velocità si possono avere neutroni la cui lunghezza d'onda è di migliaia di ångström (10³ Å=10^-5 cm=0,1 μm) (v. Ringo, 1957; v. Gurevich e Tarasov, 1968).

4. Le principali proprietà del neutrone.

Le principali proprietà del neutrone in quiete sono raccolte nella tab. I, insieme a quelle del protone che fungono da termini di confronto. Le masse di questi due corpuscoli sono date nelle prime due colonne, sia in unità di massa atomica che in grammi.

Nella terza colonna sono date le corrispondenti energie di quiete mc², espresse in MeV, le quali, per molti problemi, sono assai più significative delle masse. Come si vede, la differenza

m_nc²−m_pc²=1,2933 (±1) MeV (9)

è molto piccola (solo 1,4 per mille di m_nc²), in accordo qualitativo con le prime stime grossolane fatte da Chadwick. Su questo punto torneremo alla fine del cap. 5.

Nella quarta colonna è riportata la carica elettrica Q in termini della carica elementare, data nell'eq. (1), e nella quinta lo spin o momento della quantità di moto intrinseco J espresso nell'unità quantistica

dove h è la costante di Planck. Il neutrone, infatti, al pari del protone e dell'elettrone, si comporta come un piccolo giroscopio o trottola. L'impiego dell'unità di misura ℏ è suggerito dalla meccanica quantistica, la quale stabilisce che il momento della quantità di moto totale di un sistema qualsiasi, espresso in questa unità, è sempre pari o a un numero intero o a un numero semintero. Questa previsione, pienamente confermata dall'esperienza, è collegata a un'altra importante proprietà dei corpuscoli. Come è stato mostrato da M. Fierz e W. Pauli (1939), i corpuscoli che posseggono spin semintero ubbidiscono al principio di Pauli e quindi seguono la statistica di Fermi, mentre quelli con spin intero non ubbidiscono al principio di Pauli e seguono l'altra statistica quantistica, la statistica di Bose-Einstein. Allo scopo di marcare questa distinzione fondamentale, i corpuscoli con spin semintero vengono chiamati ‛fermioni' e quelli dotati di spin intero ‛bosoni'. Si può quindi concludere che il neutrone, come il protone, l'elettrone, ecc., è un fermione e ubbidisce perciò alla statistica di Fermi.

Nella sesta colonna della tab. I sono dati i momenti magnetici del neutrone e del protone espressi in magnetoni nucleari

Essi sono considerati come anomali nel senso che ora si cercherà di chiarire. Dopo che fu riconosciuto, all'inizio degli anni trenta, che il comportamento degli elettroni era descritto, se non esattamente per lo meno con assai buona precisione, dall'equazione di Dirac, era naturale ammettere che anche le altre particelle diverse dall'elettrone, ma dotate di spin eguale a ½, potessero essere descritte dalla stessa equazione. Ma, se si applica l'equazione di Dirac al protone e al neutrone, si trova che il primo deve avere un momento magnetico pari a un magnetone nucleare e che il secondo deve avere momento magnetico nullo. Questo secondo risultato, del resto, è piuttosto intuitivo se ci si serve dell'immagine classica secondo cui il momento magnetico di una particella carica (come l'elettrone o il protone) è dovuto alle correnti elettriche generate dallo stesso moto di rotazione attorno all'asse di simmetria della particella che dà origine al suo spin. Per una particella intrinsecamente neutra, correnti di questo tipo non esistono e pertanto ci si attenderebbe che il corrispondente momento magnetico fosse nullo. Quest'immagine classica, anche se non strettamente corretta, fornisce correttamente anche il verso del momento magnetico, che per il protone, carico positivamente, ha la stessa direzione e lo stesso verso dello spin, mentre per l'elettrone, carico negativamente, ha la stessa direzione ma verso opposto.

Il fatto che il protone e il neutrone siano dotati di momenti magnetici anomali costituisce una chiara indicazione di una struttura complessa di questi due corpuscoli (v. sotto, capp. 5 e 6). Si noti inoltre che il segno negativo del momento magnetico del neutrone indica che il suo verso è opposto a quello dello spin, ossia coincide con il verso che si dedurrebbe dall'immagine classica a cui si è accennato sopra, se nel neutrone vi fosse, per esempio, una distribuzione di carica positiva nella zona centrale, contornata da una distribuzione di carica negativa tale da dare complessivamente carica totale nulla.

Questo e altri problemi connessi con la struttura elettromagnetica del neutrone verranno discussi più dettagliatamente nel cap. 6. Qui basti ancora ricordare il problema di stabilire se il neutrone possegga o no un momento di dipolo elettrico D. Questo quesito, sollevato originariamente da E. M. Purcell e N. F. Ramsey (1950), ha acquistato in seguito molto interesse, in quanto l'esistenza di un tale momento di una particella elementare violerebbe l'invarianza rispetto all'inversione del tempo. Due misure assai accurate (dovute, la prima a Ramsey, 1967, la seconda a Shull, 1967), eseguite entrambe con neutroni lentissimi, ma con metodi diversi, hanno dato i seguenti valori:

dai quali si può concludere che il neutrone non possiede un momento di dipolo elettrico di valore apprezzabile.

Infine nella tab. I è data la vita media del neutrone. Questo corpuscolo, infatti, è instabile, come del resto era prevedibile in base al fatto che la sua energia di quiete è maggiore non solo di quella del protone, ma anche della somma delle energie di quiete del protone e dell'elettrone. Usando i valori di queste grandezze noti al giorno d'oggi si ha

Si sa oggi che il neutrone libero decade secondo il processo:

¹₀n→¹₁p+e^-+ν̄_e, (14a)

ossia si trasforma spontaneamente in un protone, emettendo un elettrone (e^-) e un antineutrino (ν̄_e).

Si è parlato di neutroni liberi, in quanto il loro comportamento, quando essi sono legati in un nucleo, è determinato dal fatto che siano o no soddisfatte certe condizioni di stabilità riguardanti il nucleo nel suo insieme. Nei nuclidi stabili il processo (14a) è reso impossibile da condizioni energetiche, che invece non sono soddisfatte nei nuclidi radioattivi per emissione di elettroni: in questi, uno dei neutroni presenti subisce il processo (14a) con una vita media determinata dalla struttura del particolare nucleo considerato. Nel caso dei nuclei instabili per emissione di elettroni positivi (come per es. il ³₁0₅P del processo 3) si hanno invece condizioni energetiche tali che uno dei protoni presenti può trasformarsi in un neutrone secondo il processo

¹₁p→¹₀n+e⁺+ν_e. (14b)

Il neutrone libero è dunque una particella debolmente instabile che decade con una vita media di circa 15 minuti e mezzo, a differenza del protone per il quale è stato stabilito un limite inferiore della vita media di 2×10²⁸ anni (M. Goldhaber e altri, 1965), assai superiore all'età dell'Universo che si stima sia dell'ordine di 10¹⁰ anni.

5. I diversi tipi d'interazione del neutrone con le altre particelle.

Una descrizione completa delle proprietà del neutrone richiede l'esame delle sue interazioni con le altre particelle, anche perché sono proprio queste a determinare ‛tutte' le sue proprietà, in particolare le proprietà discusse nel capitolo precedente.

Il neutrone, al pari del protone, possiede tutte le interazioni oggi note: interazioni gravitazionali, interazioni deboli, interazioni elettromagnetiche e interazioni forti. Che il neutrone sia soggetto alle forze gravitazionali è dimostrato dal fatto che su di una distanza dell'ordine di cento metri circa un fascio di neutroni di energia estremamente bassa, inizialmente orizzontale, mostra una curvatura apprezzabile verso il basso, tanto da permettere una discreta determinazione dell'accelerazione di gravità. Si sa inoltre che il rapporto fra massa gravitazionale e massa inerziale si mantiene costante entro alcune parti su 10¹² (B. Braginsky e altri, 1971) quando si passa da elementi pesanti, come il Pt, a elementi leggeri, come l'Al. Si può quindi concludere che un neutrone attrae ed è attratto con la forza di gravitazione universale di Newton da un altro neutrone o da un protone o da un elettrone. Come è facile verificare, facendo uso dei valori delle masse dati nella tab. I, tale forza è così piccola da risultare trascurabile anche rispetto all'interazione debole.

Il neutrone possiede anche l'interazione debole, come è dimostrato dai processi di disintegrazione (14) che sono caratteristici di questa interazione. Oggi si conoscono anche altri tipi di processi dovuti alle interazioni deboli, ma i processi (14) sono stati storicamente i primi a essere scoperti. Essi furono introdotti da Fermi nel 1933 come punto di partenza della sua teoria della disintegrazione beta dei nuclei (v. Fermi, 1962), la quale, ampliata e approfondita grazie a un notevole lavoro sperimentale e teorico, soprattutto a partire dal 1956, conserva ancora la sua validità essenziale.

Le interazioni elettromagnetiche sono in generale molto più intense delle interazioni deboli: già si è detto qualche cosa a questo riguardo nel cap. 4 e qualche maggior dettaglio sarà dato nel cap. 6, in cui verranno forniti gli elementi per effettuare un confronto fra il comportamento elettromagnetico del neutrone e il comportamento elettromagnetico del protone.

Restano infine le interazioni forti, le quali sono circa mille volte più intense delle interazioni elettromagnetiche. Nel caso di neutroni e protoni di energia non troppo elevata esse vengono indicate con il nome di ‛forze nucleari', in quanto sono queste interazioni che, agendo fra le varie particelle costituenti il nucleo, determinano l'energia di legame e i livelli energetici eccitati del nucleo e le distribuzioni spaziali dei protoni e dei neutroni che lo compongono (v. nuclei atomici: Struttura dei nuclei).

Molte informazioni sulle proprietà di queste forze sono state dedotte, oltre che dallo studio dei nuclei, da esperienze d'urto neutrone-protone e protone-protone, eseguite a partire dalle energie più basse, di qualche frazione di eV, sino alle più alte, di circa 1500 GeV, oggi raggiungibili per mezzo dei grandi acceleratori.

Tali forze vengono descritte mediante un potenziale solo per energie non troppo elevate, dato che questo concetto è valido solo in condizioni non relativistiche (E≪mc²). Questo potenziale nucleare v(r) dipende oltre che dalla distanza anche da altre variabili. Per quanto riguarda la sua dipendenza da r, si può dire, grosso modo, che a distanze molto brevi il potenziale delle forze nucleari è fortemente repulsivo, diventa attrattivo a distanze dell'ordine di 0,4÷0,5×10^-13 cm e poi decresce al crescere di r secondo la legge di H. Yukawa (1936)

dove A è una costante e

è la lunghezza d'onda Compton del pione (_mπc²=140 MeV, d≃1,4×10^-13 cm).

La funzione v(r) (e quindi la costante A) dipende poi dallo ‛stato' dei due corpuscoli, come chiariremo fra breve. Ma, a parità di stato, il potenziale nucleare è indipendente dalla carica elettrica dei due corpuscoli: in altre parole, è lo stesso se le due particelle che interagiscono sono due neutroni, oppure un neutrone e un protone, oppure due protoni, a condizione, naturalmente, che si tenga conto a parte delle forze elettromagnetiche. Su questa legge dell'indipendenza dalla carica delle forze nucleari si tornerà fra breve.

La dipendenza di v(r) dallo stato può essere precisata come segue: innanzitutto v(r) è diverso a seconda che gli spins dei due corpuscoli siano antiparalleli fra loro (in modo che la loro somma S sia uguale a zero: stati di singoletto) o paralleli fra loro (S=1: stati di tripletto). Negli stati di singoletto le forze sono puramente centrali, mentre negli stati di tripletto si debbono aggiungere, a un termine centrale diverso dal precedente, un termine detto ‛spin-orbita' dipendente dal prodotto S•l (dove l è il momento della quantità di moto orbitale del moto relativo dei due corpuscoli, in unità ℏ) e un termine non centrale, detto ‛tensoriale', che dipende anche dall'angolo formato dagli spins dei due corpuscoli con il vettore r.

Non è certo possibile in questa sede discutere nei parti- colari le proprietà di queste forze, se non per due caratteristiche qualitative fondamentali che stanno alla base di tutta la descrizione attuale dei fenomeni nucleari e subnucleari. La prima riguarda l'indipendenza a parità di stato del potenziale nucleare dalla carica elettrica. Questa proprietà, insieme alla piccola differenza fra le masse del neutrone e del protone, suggerisce l'idea che il protone e il neutrone non siano due oggetti indipendenti, ma piuttosto due stati diversi di un unico corpuscolo: il ‛nucleone'. A questo corpuscolo si deve attribuire un grado di libertà interno, descritto da una nuova variabile che può assumere due soli valori, uno dei quali individua lo stato protone, l'altro lo stato neutrone. Come vedremo fra un momento, questo punto di vista trova il suo sostegno nella teoria del campo mesonico. Uno studio approfondito della legge dell'indipendenza dalla carica ha mostrato che una sua rappresentazione matematica corretta comporta l'introduzione del concetto di ‛spin isotopico' del nucleone. Questo è un vettore I, definito in uno spazio rappresentativo detto ‛isospazio', dotato delle stesse proprietà matematiche di cui gode lo spin J nello spazio ordinario; se J=½, come accade per il protone e il neutrone (v. tab. I), il vettore J può assumere due soli orientamenti nello spazio: uno parallelo (J_z=+½) e l'altro antiparallelo (J_z=−½) rispetto a un asse z che si può pensare individuato da un campo magnetico di intensità piccola a piacere.

Nel formalismo dello spin isotopico si attribuisce al nucleone uno spin isotopico I=½: tutte le volte che I è parallelo al terzo asse dell'isospazio (I₃=+½), il nucleone si trova nello stato protone, tutte le volte che I ha verso opposto (I₃=−½), il nucleone è nello stato neutrone. La carica elettrica del nucleone è data poi dalla formula

che, per I₃=−½, assume i valori 1 e 0 che competono rispettivamente al protone e al neutrone. Il concetto di spin isotopico è stato successivamente esteso a tutte le particelle dotate di interazioni forti, indicate complessivamente col nome di ‛adroni'. Con ciò è diventato possibile esprimere la legge dell'indipendenza delle interazioni forti dalla carica elettrica come legge di invarianza rispetto alle rotazioni nell'isospazio.

La teoria del campo mesonico, iniziata da H. Yukawa nel 1936, è costruita per analogia con la teoria del campo elettromagnetico: l'interazione fra due corpuscoli dotati di carica elettrica in moto viene descritta, nell'elettrodinamica quantistica, come un susseguirsi di processi di emissione di un fotone - cioè di un quanto del campo elettromagnetico - da parte di uno dei due corpuscoli e di assorbimento da parte dell'altro e viceversa (v. fig. 2A).

Nella teoria del campo mesonico, l'interazione forte fra due adroni, in particolare fra due nucleoni, viene descritta come un succedersi di processi di emissione di un mesone - cioè di un quanto del campo mesonico - da parte di uno dei due adroni e di assorbimento da parte dell'altro e viceversa (v. fig. 2B). I mesoni che possono essere scambiati fra due nucleoni sono di diverso tipo (π, ρ, σ, ...) e alcuni di essi possono trovarsi in diversi stati di carica elettrica; l'emissione di un mesone positivo è accompagnata dalla trasformazione in neutrone del protone che lo emette e dalla trasformazione in protone del neutrone che lo assorbe; un processo di questo tipo corrisponde a uno scambio delle coordinate spaziali di due nucleoni e dà luogo a ‛forze di scambio' del tipo di quelle ipotizzate da E. Majorana nel 1933. Lo scambio, invece, di un mesone neutro tra due nucleoni dà luogo alle forze ordinarie o alla Wigner (v. nuclei atomici: Struttura dei nuclei).

Ma anche un nucleone, o più in generale un adrone, isolato emette e riassorbe continuamente mesoni virtuali, carichi o neutri, di diverso tipo secondo processi che possono essere indicati schematicamente come segue:

In queste relazioni p ed n indicano il protone e il neutrone ‛fisici' ossia quelli effettivamente osservati, mentre >p〈 ed >n〈 rappresentano i corrispondenti ‛corpuscoli nudi' ossia svestiti della loro nuvola mesonica, che è indicata a parte nel secondo membro delle (17).

Sono proprio i processi del tipo di quelli indicati dalle relazioni (17) che danno luogo alla struttura alquanto complessa dei nucleoni fisici. Per esempio, nel caso del neutrone, il fatto che parte del tempo esso sia per così dire dissociato in un protone nudo contornato da una nuvola mesonica carica negativamente dà, almeno qualitativa- mente, ragione del suo momento magnetico anomalo (v. tab. I) e dei fattori di forma elettromagnetici G_En(q²) e G_Mn(q²), di cui parleremo nel cap. 6. Si è detto qualitativa- mente, perché il calcolo di queste proprietà dei nucleoni, partendo dalla teoria del campo mesonico, non ha sino a oggi portato a risultati quantitativamente soddisfacenti.

6. La struttura elettromagnetica del neutrone.

Due diversi tipi di esperienze, basati entrambi sullo studio dell'interazione fra il neutrone e l'elettrone, permettono di determinare sperimentalmente la struttura elettromagnetica del neutrone.

Un primo tipo di esperimenti è quello iniziato da R. Hofstadter nel 1953 a Stanford, negli Stati Uniti, e successivamente applicato sistematicamente ed esteso dal suo e da altri gruppi. Si tratta di esperimenti concettualmente simili all'esperimento suggerito da E. Rutherford ed eseguito per la prima volta da Geiger e Marsden, che permise, a partire dal 1910, di determinare la struttura dell'atomo e le dimensioni del nucleo.

Gli esperimenti di Hofstadter differiscono da questi esperimenti classici per la natura dei due corpuscoli interagenti e per l'entità delle quantità di moto in gioco. Negli esperimenti destinati a determinare la struttura elettromagnetica del protone, un fascetto di elettroni di energia E₀ sufficientemente elevata, cioè di almeno qualche centinaio di MeV, incide su di un bersaglio di idrogeno liquido contenuto in un recipiente a pareti sottili. Ciò che si misura è il numero degli elettroni deviati nella direzione ϑ in seguito a un urto elastico con un protone e dotati, quindi, dopo l'urto, di un'energia E ben definita. L'esperienza permette così di determinare la sezione d'urto elastico differenziale, ossia quella riferita all'angolo solido dΩ nella direzione ϑ. Questa è data dalla formula derivata nel 1950 da M. N. Rosenbluth sotto le seguenti ipotesi molto generali: 1) il processo d'urto è descritto con buona precisione prendendo in considerazione solo processi in cui l'elettrone e il protone si scambiano un solo fotone; 2) l'elettrone si comporta come una particella di Dirac priva di struttura; 3) il fotone è un corpuscolo di massa rigorosamente nulla. Da queste ipotesi, che sono state verificate con notevole accuratezza, segue la formula di Rosenbluth:

dove sono state adottate unità tali che c=ℏ=1, e

è la sezione d'urto di Mott, cioè la sezione d'urto che si avrebbe se il protone fosse puntiforme. La quantità fra parentesi quadre congloba l'effetto della struttura del protone; in essa figurano i ‛fattori di forma' elettrico, G_Ep(q²), e magnetico, G_Mp(q²), del protone, che sono funzioni sempre reali di q², normalizzate in modo che, per q²=0,risulti:

G_Ep(0) =1 e G_Mp(0)=μ_p.

La variabile q² si chiama quadrato del ‛quadrimomento' trasferito dall'elettrone al protone; essa è data da

q²=(E₀−E)²−(p₀−p)², (19)

dove E₀, p₀, E e p sono le energie totali e le corrispondenti quantità di moto dell'elettrone prima e dopo l'urto. Il quadrimomento trasferito q² è una grandezza relativisticamente invariante, ossia una grandezza che ha lo stesso valore in qualunque sistema di riferimento. Anche i fattori di forma G_Ep e G_Mp godono evidentemente della stessa proprietà.

Se q²>0 si dice che il quadrimomento trasferito è del tipo ‛temporale', se q²〈0 si dice che è del tipo ‛spaziale'. È facile convincersi che nel caso qui discusso dell'urto elastico, fra elettrone e protone, si ha sempre q²〈0.

Per comprendere in che senso i fattori di forma descrivano - nel modo più generale possibile - la struttura elettromagnetica del protone, ci si ponga nel sistema di riferimento in cui il protone è fermo e la sua struttura elettromagnetica può essere descritta assegnando le distribuzioni spaziali di carica, ρ_Ep(r), e di magnetizzazione, ρ_Mp(r).

Come conseguenza del fatto che l'urto elettrone-protone è elastico, in questo riferimento si ha E=E₀, ∣p∣=∣p₀∣ e quindi q² si riduce al quadrato della quantità di moto trasferita dall'elettrone al protone, ossia

e i fattori di forma non sono altro che le trasformate di Fourier delle funzioni di distribuzione sopra indicate,

In queste formule r è misurato in cm e q, con le unità qui usate, in cm^-1, oppure r in Fermi (1 F=10^-13 cm) e quindi q² in F^-2. Talvolta invece si esprime q² in (GeV/c)², essendo 1(GeVc)²≃25 F^-2.

Come si vede dalla (18a), se si misura dσ/dΩ per diversi valori di ϑ mantenendo q²=costante e si costruisce un grafico di (dσ/dr)/σ₀ in funzione di tg² ϑ/2, si ottiene una retta la cui pendenza e la cui intersezione con l'asse delle ordinate corrispondono rispettivamente ai valori delle quantità

e

Dai valori ottenuti per queste due espressioni si ricavano i valori sperimentali di G_Ep(q²) e G_Mp(q²) corrispondenti al prescelto valore di q².

Una volta determinati sperimentalmente i fattori di forma, basta invertire la (20) per dedurre le distribuzioni di carica e di magnetizzazione del protone,

Partendo dalla (20) e dalla (21) è poi facile dimostrare che, indipendentemente dalla forma particolare delle funzioni che vi figurano, si ha sempre

dove

>r²〈= ∫ r²ρ(r) d³r. (23)

Lo stesso metodo può venir usato, in linea di principio, anche nel caso del neutrone: per questo corpuscolo vale ancora la (18) con le corrispondenti grandezze relative al neutrone scritte al posto di m_p, G_Ep e G_Mp. In questo caso pero il fattore di forma magnetico è normalizzato in modo che risulti

G_Mn(0)=μ_n.

Si ha poi, necessariamente,

G_En(0)=0,

come conseguenza del fatto che la carica totale del neutrone è nulla.

Nel caso del neutrone, però, non si dispone di un bersaglio costituito solo di neutroni; si è quindi costretti a usare idrogeno pesante liquido, il cui nucleo (deutone) è costituito da un protone e da un neutrone legati fra loro. Poiché entrambe queste particelle interagiscono con gli elettroni incidenti, per ricavare dai dati sperimentali i fattori di forma G_En(q²) G_Mn(q²) è necessario detrarre dalla sezione d'urto misurata l'effetto dei protoni, misurato in precedenza, e applicare alcune correzioni. Ciò significa che i valori sperimentali dei fattori di forma del neutrone sono affetti da incertezze assai maggiori di quelle relative al protone, soprattutto per ciò che riguarda G_En(q²), che è molto piccolo.

Le figg. 3, 4, 5 e 6 mostrano i risultati ottenuti da diversi autori, entro il 1971, mediante esperienze del tipo sopra descritto (v. Bartoli e altri, 1972). Da questi risultati si possono dedurre alcune conseguenze molto interessanti.

1. Il fattore di forma elettrico del protone (v. fig. 3) è rappresentato con buona approssimazione, per bassi valori di −q² dalla cosiddetta espressione dipolare

Per −q²>30 F^-2 circa le deviazioni dei punti sperimentali da questa legge possono anche essere del 20 o 30%.

2. Dal confronto dei risultati riportati nelle figg. 3, 4 e 6, sembra che valgano approssimativamente (per elevati valori di −q², solo entro il 30%) le seguenti ‛leggi di scala':

suggerite da argomenti teorici piuttosto deboli.

L'espressione analitica dipolare (24a) non ha peraltro alcuna giustificazione teorica sicura; pertanto le espressioni usate per rappresentare i tre fattori di forma, G_Ep, G_Mp, G_Mn, vanno considerate solo come formule di interpolazione dei dati sperimentali. Se, ciò nonostante, si applica l'inversione (21) alla (24a) si ottiene:

ρ_Ep(r)≃3,06 e^-4,25r, con r in F. (25)

Quest'espressione è assai utile per dare un'idea della distribuzione spaziale della carica del protone e della magnetizzazione sia del protone sia del neutrone; essa va tuttavia presa con riserva, in quanto, se si usasse una formula diversa dall'espressione dipolare (24a), ma tale da rappresentare altrettanto bene i dati sperimentali, la sua trasformata di Fourier sarebbe in generale molto diversa dalla (25).

Un risultato indipendente dall'uso di particolari formule d'interpolazione è quello relativo al raggio quadratico medio del protone, che si ricava introducendo nel primo membro della (22) la pendenza iniziale dei fattori di forma del protone, misurata sperimentalmente. Si ottiene così:

√-〈--r-_p--²-->=0,81 F, (26a)

in ottimo accordo con il valore che si può calcolare mediante la (24a).

Per quanto riguarda G_En(q²) (v. fig. 5) la situazione è ancor oggi assai meno chiara. Le tre curve tracciate nella figura corrispondono a tre diversi modelli: la curva a punto e linea corrisponde a

la curva tratteggiata a

e la curva a linea continua a

dove b è un parametro che è stato determinato (b=5,6) in modo da ottimizzare la rappresentazione dei punti sperimentali.

Non è qui il caso di addentrarsi in una discussione di questi diversi modelli; ciò che è sicuro è che G_En(q²) è apprezzabilmente diverso da zero per valori di −q² compresi fra 4 e 20 F^-2.

Da questi diversi modelli di G_En, si può ricavare mediante la (22) il raggio quadratico medio della distribuzione di carica del neutrone. Il valore così trovato risulta in buon accordo con i risultati delle misure basate sull'altro metodo che passiamo a descrivere.

Negli esperimenti di quest'altro tipo si determina la sezione d'urto elastico totale, contro gli elettroni di un atomo di elevato numero atomico, di un neutrone così lento che la sua lunghezza d'onda sia dello stesso ordine di grandezza o anche maggiore delle dimensioni atomiche.

Esperimenti di questo tipo presentano la difficoltà che l'effetto globale degli Z elettroni dell'atomo, anche se di numero atomico elevato (come nel caso del bismuto: Z=83), ammonta a solo circa l'1% della sezione d'urto totale del neutrone contro il nucleo dell'atomo stesso. Questa difficoltà è stata superata dai diversi autori ricorrendo ad artifici, molto ingegnosi ed eleganti, che permettono talvolta di separare i due effetti, talaltra di compensare quasi esattamente l'effetto dell'urto neutrone-nucleo.

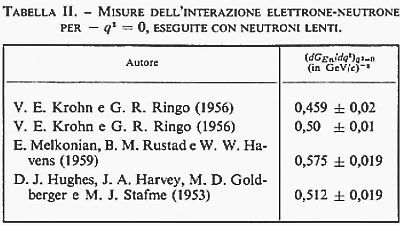
Fin dai primi esperimenti di questo tipo (E. Fermi e L. Marshall, 1947; I. I. Rabi e altri, 1947) è stata dimostrata l'esistenza di una debole interazione elettrone-neutrone, la quale può essere espressa in termini della derivata di G_En(q²), calcolata per q²=0, oppure, grazie alla (22), in termini di >r²〈 (v. Ringo, 1957).

I risultati ottenuti più recentemente dai vari autori sono riassunti nella tab. II. A essi corrisponde

√-〈-r-_n-²->≃0,35 F, (26b)

cioè un valore piuttosto elevato, se confrontato con il raggio (26a) del protone.

Nulla si sa oggi, invece, della struttura elettromagnetica del neutrone per valori di q² di tipo temporale (q²>0), anche se la sua determinazione sperimentale è possibile in linea di principio attraverso misure della sezione d'urto del processo

e⁺+e^-→n+ò,

dove con ò si è indicato l'antineutrone. Solo negli ultimi anni sono state fatte alcune misure di questo tipo con l'anello d'accumulazione Adone dei Laboratori Nazionali di Frascati del CNEN e con altre macchine di questo stesso tipo, ma per il processo

e⁺+e^-→p+ä,

dove con ä si è indicato l'antiprotone. I risultati, molto interessanti, non vengono qui riportati, in quanto non riguardano la struttura del neutrone.

A conclusione di questo capitolo è necessario accennare a due altri fatti molto importanti. Il primo consiste nei risultati dello studio sperimentale dell'urto anelastico di elettroni di energia molto elevata contro protoni o neutroni; la loro interpretazione sembra richiedere che la carica del protone, o del neutrone, sia concentrata in un numero n (≥3) di componenti puntiformi, di dimensioni, cioè, molto più piccole di quelle del nucleone. Tali componenti puntiformi, secondo la nomenclatura introdotta da R. R. Feynman, vengono chiamati ‛partoni'. Le esperienze sono simili a quelle sopra descritte per la determinazione dei fattori di forma elettromagnetici del nucleone. Esse ne differiscono, tuttavia, perché l'urto è anelastico, cioè ha luogo con una perdita di energia

ν=E₀^*−E^* (27)

da parte dell'elettrone, che passa così dall'energia iniziale E₀^* a un'energia finale minore E^*, misurate entrambe nel riferimento del centro di massa del sistema elettrone-protone; l'energia ν viene impiegata nella produzione di uno o più adroni. Questi non vengono però osservati nelle esperienze qui discusse, dette ‛esperienze inclusive', in quanto lo stato finale del sistema è individuato dalla sola quantità di moto p dell'elettrone dopo l'urto.

La misura della sezione d'urto permette di ricavare le cosiddette ‛funzioni di struttura' per l'urto anelastico. Queste sono in qualche modo analoghe ai fattori di forma elettromagnetici sopra discussi, ma, a differenza di questi, dipendono da due variabili: il quadrimomento trasferito e la perdita di energia, la quale nel caso dell'urto elastico è per definizione eguale a zero. L'impiego dell'acceleratore lineare dell'Università di Stanford, capace di produrre elettroni con energia di 20 GeV, ha permesso di stabilire una nuova legge Sperimentale molto importante: per valori sufficientemente elevati di entrambe le variabili ν e q², ossia in condizioni di urto profondamente anelastico, le funzioni di struttura sopra citate non dipendono più dai valori di queste due variabili prese separatamente, ma solo dal valore del loro rapporto ν/q².

Questo risultato, noto come ‛legge di scala', era stato previsto teoricamente da J. D. Bjorken (1969) e viene ora facilmente interpretato ammettendo che il protone sia costituito da componenti puntiformi, ciascuno dotato di una carica più piccola di quella e dell'elettrone e di spin J=½, detti appunto ‛partoni'. Risultati analoghi sono stati ottenuti anche con anelli di accumulazione per elettroni e positroni come Adone e altre macchine simili.

Anche il neutrone mostra un comportamento analogo a quello del protone, pur restando naturalmente inteso che la somma delle cariche dei corrispondenti partoni è, in questo caso, necessariamente uguale a zero.

Questi risultati non sono in alcun modo in contraddizione con quanto detto sopra a proposito dei fattori di forma G_E e G_M: per energie degli elettroni incidenti di qualche GeV, osservando gli elettroni deviati nell'urto anelastico ad angolo elevato (urto profondamente anelastico), si possono rivelare dei dettagli di struttura che sfuggono all'osservazione quando ci si pone nelle condizioni d'urto elastico.

L'altro fatto a cui è ancora necessario accennare è che anche per le interazioni deboli si possono definire dei fattori di forma G_A(q²) e G_P(q²) del protone e del neutrone simili ai fattori di forma elettromagnetici G_E(q²) e G_M(q²). Le misure di queste grandezze sono ancora in uno stadio non molto avanzato e pertanto non vengono qui riportate. Quello che si può dire è che ci sono buone indicazioni per una dipendenza di G_A(q²) da q² del tipo di quella dipolare data dalla (24a), salvo che il valore della costante che figura in tale espressione è sensibilmente diverso da quello relativo a G_Ep(q²).

7. Le sorgenti di neutroni.

Le sorgenti di neutroni possono essere del tipo più diverso: un'ampollina di vetro contenente polvere di berillio mescolata a un corpo radioattivo che emetta particelle alfa (v. fig. 7), acceleratori di particelle cariche, reattori nucleari di ricerca (v. figg. 8 e 9). Si è quindi costretti, in questa sede, a riportare solo alcuni esempi (v. Amaldi, 1959).

Le sorgenti usate nelle prime ricerche che portarono alla scoperta del neutrone (v. cap. 2) e ai primi studi delle sue proprietà (v. cap. 3) erano tutte basate sulle reazioni (α, n) prodotte negli elementi leggeri. Nel caso del berillio, l'elemento che fornisce maggiore intensità, la reazione è

4⁹Be+4₂He→¹²₆C+0¹n+5,7 MeV, (28)

dove è indicata anche l'energia che si libera in questo processo esoenergetico.

Come corpi emettitori alfa si usavano allora, e si usano ancor oggi, a seconda dei casi, ²¹⁰P0, ²²⁶Ra, ²²²Rn, ai quali si sono aggiunti più tardi ²³⁹Pu, ²⁴¹Am, ²⁴²Cm. Nella fig. 7 è mostrata la fotografia di una delle sorgenti usate, negli anni 1934-1936, dal gruppo di Fermi; nell'ampollina di vetro è contenuto Be in forma di granuli metallici, mescolati a emanazione di radio (²²²Rn); il tubo di vetro, lungo una trentina di centimetri, serviva solo per il maneggio della sorgente.

Sorgenti di questo tipo, contenenti corpi radioattivi alfa a lunga vita media (per es. il ²²⁶Ra, che ha un periodo di dimezzamento di 1.600 anni), sono usate ancor oggi come sorgenti standard. Una sorgente contenente Ra+Be emette, su tutto l'angolo solido, circa 1,4•10⁷ neutroni al secondo, per grammo di Ra.

Quando si disponga di un acceleratore che permetta di accelerare protoni, deutoni o tritoni (³₁T=³₁H) sino a energie dell'ordine di qualche MeV, si preferiscono altre reazioni. Alcuni esempi, particolarmente interessanti, sono i seguenti:

²₁D+²₁D→³₂He+0¹n+3,27 MeV (29a)

1²D+1³H→4₂He+0¹n+17,6 MeV (29b)

¹₁p+³₁H→³₂He+0¹n−0,764 MeV. (29c)

La scelta dell'una o dell'altra di queste reazioni dipende dall'acceleratore di particelle di cui si dispone e dallo spettro di neutroni (veloci) che si desidera produrre. Le tre reazioni qui riportate hanno la caratteristica comune che nello stato finale vi sono due corpi soli. In queste condizioni, lo spettro dei neutroni che si osserva in una ben determinata direzione rispetto al fascio delle particelle incidenti è monoenergetico, purché il nucleo residuo si possa formare solo nello stato fondamentale; ciò è quanto accade negli esempi riportati, se l'energia della particella incidente non è troppo grande. La reazione (29a) ha il vantaggio sulle altre di aver luogo con un rendimento apprezzabile già per energie del deutone incidente comprese tra 0,2 e 0,3 MeV; la reazione (29b), essendo fortemente esoenergetica, fornisce, a parità di energia delle particelle incidenti, neutroni di energia più elevata; la reazione (29c) è un po' endoenergetica, ma per certe esperienze può presentare qualche vantaggio rispetto alle precedenti.

Le reazioni (29) hanno il vantaggio, rispetto alle reazioni (α, n) del tipo della (28), di fornire neutroni con intensità assai maggiore come conseguenza di due fatti. Il primo è che, per energie non molto elevate, le particelle incidenti, essendo dotate di carica elettrica metà di quella delle particelle α, penetrano più facilmente entro il nucleo bombardato; il secondo fatto, anche più importante, è che il fascio incidente fornito da un acceleratore contiene molte più particelle di quelle emesse da un corpo radioattivo. Basti pensare che 1 μA di protoni corrisponde a 6,25×10¹² protoni/secondo, mentre un grammo di radio emette 3,7×10¹⁰ particelle α/secondo. Infine, variando opportunamente l'energia fornita dall'acceleratore e la direzione in cui vengono osservati i neutroni, si può far variare entro limiti piuttosto ampi l'energia dei neutroni su cui si vuol sperimentare.

Altre reazioni che vengono talvolta usate per produrre neutroni sono le reazioni (γ, n), due esempi particolarmente importanti delle quali sono i seguenti:

hν+²₁D→¹₁H+0¹n−2,227 MeV (30a)

hν+9₄Be→8₄Be+0¹n−1,666 MeV. (30b)

Come raggi gamma incidenti si possono usare sia quelli emessi da corpi naturalmente radioattivi o prodotti in certe reazioni nucleari, sia i cosiddetti raggi gamma di Bremsstrahlung, che si producono quando gli elettroni forniti da un acceleratore sono rallentati nell'attraversare un opportuno bersaglio. Con i raggi gamma di un corpo radioattivo che emetta fotoni di una sola energia, le reazioni (30) forniscono neutroni monoenergetici di energie dell'ordine del MeV o inferiori; con i raggi gamma di Bremsstrahlung si ottiene uno spettro continuo di neutroni che, per energie degli elettroni sufficientemente elevate, può estendersi fino a 20 o 30 MeV.

Per produrre neutroni di energia superiore a circa 50 MeV non si fa più ricorso alle reazioni (29) e (30), ma a due altri tipi di processi (v. Marion e Fowler, 1960; v. Phillips e altri, 1963): le reazioni di strappo, o stripping, del deutone e l'urto con scambio di carica di un protone contro un neutrone di un nucleo. Nei processi di strappo un deutone incidente, per esempio di circa 100 MeV, passando vicino al bordo di un nucleo si ‛strappa': il suo protone resta, per così dire, catturato nel nucleo, che subisce successivamente uno o più processi di disintegrazione, mentre il suo neutrone prosegue in una direzione prossima a quella del deutone incidente con circa metà dell'energia cinetica che questo possedeva inizialmente (nel nostro esempio circa 50MeV).

I processi di scambio di carica vengono usati alle grandissime energie, dell'ordine del GeV e oltre, e consistono nel fatto che, a queste energie, il protone incidente, nell'attraversare un nucleo, dà luogo abbastanza frequentemente a un urto con uno dei neutroni circostanti, che è molto simile a un urto elastico, salvo il fatto che i due corpuscoli si scambiano le loro cariche elettriche. Questo processo viene facilmente interpretato nel quadro delle concezioni esposte alla fine del cap. 5, secondo cui il protone e il neutrone sono due stati diversi di uno stesso corpuscolo, il nucleone: lo scambio di carica è dovuto al trasferimento di un mesone carico positivamente dal protone incidente al neutrone urtato. Il corpuscolo che rincula è diventato un protone mentre quello incidente è diventato un neutrone che prosegue con una quantità di moto p non molto diversa, in direzione e modulo, da quella che possedeva inizialmente.

Per produrre neutroni lenti, ci si può servire di una qualunque delle sorgenti descritte sopra, contornata da un moderatore. Le sorgenti di gran lunga più intense di neutroni lenti sono tuttavia costituite dai reattori nucleari. Per esempio, il reattore delle figg. 8 e 9 ha un flusso termico massimo (nel riflettore) di 1,5×10¹⁵ neutroni al cm² e al secondo e un flusso massimo di neutroni veloci (E>0,821 MeV), sul mantello esterno, di 3,5×10¹⁴ neutroni al cm² e al secondo. Questi valori saranno certamente superati nei reattori che si costruiranno in avvenire.

In natura si osservano neutroni di alta energia nei raggi cosmici; questi sono però di origine secondaria, ossia prodotti nell'alta atmosfera da parte dei raggi cosmici primari che sono costituiti prevalentemente da protoni e, in piccola percentuale, da nuclei di elementi leggeri medi e pesanti dotati di altissime energie, fino a 10²⁰ eV, provenienti dagli spazi interstellari.

Si ritiene oggi che il Sole debba emettere neutroni, per lo meno in occasione dei brillamenti solari, ma per ora non sono stati osservati. Il giorno in cui si osservassero, diventerebbe naturale ammettere che anche altri corpi celesti siano sorgenti naturali di neutroni. Ma la vita media dei neutroni è così breve (v. tab. I) che, anche tenendo conto della dilatazione relativistica del tempo, essi non potrebbero sopravvivere a viaggi così lunghi nello spazio quali sono necessari per giungere sulla Terra da qualsiasi astro diverso dal Sole.

8. Le reazioni prodotte da neutroni.

Le reazioni prodotte da neutroni note al giorno d'oggi, o tuttora allo studio, sono così numerose e di tipi così diversi da rendere impossibile una loro descrizione, anche sommaria, in questa sede. Esse inoltre vanno sempre esaminate nel quadro più generale di tutti i processi che possono essere prodotti, invece che da neutroni, da altri corpuscoli, come i protoni, i deutoni, le particelle alfa, ecc. ; i primi, infatti, sono semplicemente nucleoni in uno stato di carica diverso dallo stato neutrone, mentre gli altri sono aggregati di due o più nucleoni. Si tratta, comunque, sempre di corpuscoli dotati di interazioni forti o adroni (v. sopra, cap. 5) e quindi di oggetti ben diversi dai leptoni (muoni, elettroni, neutrini), i quali non posseggono interazioni forti ma solo elettromagnetiche e deboli (v. particelle elementari: Campi e particelle).

Chiarita questa distinzione essenziale, conviene considerare separatamente tre regioni energetiche diverse: la prima, che si estende da 0 a circa 10-30 MeV, la seconda da 10-30 MeV a circa 140 MeV e la terza oltre i 140 MeV.

Il fatto che il neutrone sia neutro ha una notevole importanza solo alle basse energie (prima regione), alle quali un corpuscolo carico, come un protone o un deutone (Q=e) o una particella alfa (Q=2e), per penetrare in un nucleo deve attraversare la barriera elettrostatica di potenziale dovuta all'effetto delle forze coulombiane repulsive dei protoni. La probabilità che ha un corpuscolo carico di passare attraverso tale barriera costituisce un tipico effetto di natura quantistica; a parità di energia del corpuscolo incidente, essa è una funzione fortemente decrescente del numero atomico Z del nucleo e, a parità di numero atomico, una funzione rapidamente crescente dell'energia del corpuscolo incidente, la quale, a partire da energie dell'ordine di 10-30 MeV, a seconda del valore di Z, diventa praticamente costante e uguale a 1.

Al di sopra di queste energie (seconda regione) l'effetto della repulsione coulombiana è trascurabile anche nel caso di nuclei con Z elevato e le caratteristiche delle reazioni prodotte da protoni non sono sostanzialmente diverse da quelle prodotte da neutroni, anche se la conservazione della carica, o meglio dello spin isotopico (v. sopra, cap. 5), impone condizioni diverse nei due casi.

Quando l'energia del corpuscolo incidente, sia esso un neutrone o un protone, supera 140 MeV (nel centro di massa delle particelle urtantisi), comincia a diventare possibile la produzione di pioni (^mπc²=140 MeV); si è così di fronte a una nuova categoria di reazioni, completamente diverse dalle reazioni nucleari propriamente dette. È vero che se il nucleone con cui interagisce il corpuscolo incidente non è isolato ma appartiene a un nucleo, questo subisce un processo di disintegrazione, in generale, assai complicato; ma si tratta di un processo per così dire secondario rispetto al processo primario più interessante, che è quello della ‛generazione' del pione. Al crescere dell'energia si raggiungono successivamente le soglie che competono sia alla produzione di altri corpuscoli, dotati di energie di quiete via via più grandi, sia all'eccitazione di stati interni dei nucleoni interagenti e alla produzione diretta di molte particelle (v. particelle elementari: Campi e particelle).

Nella regione delle alte energie non ha senso parlare, come di un argomento a sé stante, delle reazioni prodotte da neutroni; è vero che in un ben determinato esperimento si userà come corpuscolo incidente un fascio di protoni oppure un fascio di neutroni, ma i risultati sperimentali acquistano un significato abbastanza chiaro solo se esaminati insieme ai risultati di altri esperimenti in un unico quadro di cui ciascuno di essi serve a mettere in luce una diversa parte.

Da questi brevi cenni di carattere generale è chiaro che, quando si parla di reazioni prodotte da neutroni come argomento a sé stante, ci si riferisce di solito alle reazioni nucleari che si osservano nella regione di energia al di sotto di 10-30 MeV, in particolare a quelle prodotte da neutroni di pochi MeV o anche meno: sono queste infatti le condizioni in cui il ‛carattere neutro' del neutrone assume un'importanza particolare. Per di più, i neutroni prodotti per fissione entro un reattore nucleare sono dotati di energie di pochi MeV ed è proprio grazie alle proprietà peculiari dei nucleoni di così bassa energia che queste macchine possono funzionare.

Oltre all'urto elastico contro i nuclei, i neutroni di pochi MeV danno luogo a diversi tipi di reazione, urto anelastico (n, n′) (v. IAEA, 1965 e 1968), (n, p), (n, α) ed (n, γ), alle qua- li va aggiunta la fissione degli elementi pesanti, come il Th e l'U, la cui trattazione è fatta in altro articolo (v. nuclei atomici: Struttura dei nuclei).

Nella maggior parte di queste reazioni, inclusa la fissione, il neutrone incidente viene catturato dal nucleo bersaglio che si trasforma così in un ‛nucleo composto' eccitato. Questo, dopo un certo tempo, che è brevissimo rispetto ai tempi di misura ma lungo rispetto al tempo di transito di un neutrone attraverso il nucleo, emette a seconda dei casi un neutrone d'energia più bassa (urto anelastico), un protone, una particella alfa, un raggio gamma oppure, nel caso dei nuclei molto pesanti, si scinde in due nuclei di elementi di massa intermedia.

Ora, la sezione d'urto totale σ_tot di un dato nucleo per neutroni di una ben determinata energia cinetica E non troppo grande si può sempre scrivere come somma di due termini:

σ_tot(E)=σ_sc(E)+σ_a(E), (31)

dove σ_sc(E) rappresenta la sezione d'urto elastico e σ_a(E) la sezione d'urto per assorbimento o cattura del neutrone incidente. Quest'ultima è poi in generale la somma delle sezioni d'urto relative a tutti i processi che sono energeticamente possibili all'energia considerata

σ_a=σ(n, γ)+σ(n, n′)+σ(n, p)+σ(n, α)+... . (32)

Ma nei processi (n, p) ed (n, α) la particella emessa è carica elettricamente; la sua uscita è ostacolata dalla stessa barriera elettrostatica di potenziale che ostacola l'ingresso delle particelle cariche incidenti, cosicché, per neutroni di qualche MeV, σ(n, p) e σ(n, α) sono trascurabili nei nuclei con Z elevato e medio, piccole nei nuclei con basso Z e decrescono ulteriormente al decrescere dell'energia del neutrone. Ne segue che, anche quando queste reazioni sono esoenergetiche, l'andamento delle corrispondenti sezioni d'urto in funzione dell'energia è in qualche modo simile a quello che si osserva nel caso dei processi endoenergetici, per i quali esiste sempre una soglia al di sotto della quale il processo non può aver luogo. Fanno eccezione solo alcuni processi (n, p) ed (n, α) esoenergetici in nuclei con Z così basso che il concetto stesso di barriera di potenziale perde significato. I tre processi più importanti di questo tipo sono:

³₂He+0¹n→³₁T+¹₁p+0,764 MeV σ=5.400 b (33a)

6₃Li+0¹n→³₁T+4₂He+4,780 MeV σ=945b (33b)

¹0₅B+0¹n→7₃Li+4₂He+2,792 MeV σ= 4.010 b, (33c)

ai quali va aggiunta la reazione (n, p) nell'¹4₇N. La sezione d'urto, indicata a lato di ciascuna delle reazioni (33), si riferisce a neutroni di 2.200 m/s (v. sopra, cap. 3, equazione 5) ed è espressa in barn (1 barn=10^-24 cm²) Come si vede, le sezioni d'urto sono enormi se confrontate con la sezione geometrica del nucleo, πR², dove

R=r₀A^1/3 (r₀≃1,2×10^-13 cm) (34)

è il raggio del nucleo. Per esempio, nel caso del ¹0₅B, si ha R=2,6×10^-13, da cui segue πR² ≃0,21×10^-24 cm²=0,21 b.

Le reazioni (n, γ) sono sempre esoenergetiche, in quanto, nel processo di legame di un neutrone in un nucleo, si liberano circa 7 o 8 MeV, che vengono emessi dal nucleo composto sotto forma di uno o più quanti gamma. Questi, al pari del neutrone incidente, non sentono in alcun modo l'effetto della barriera elettrostatica di potenziale, cosicché, alle bassissime energie, i processi (n, γ) sono, in generale, i soli che contribuiscono alla sezione d'urto di assorbimento σ_a, ossia è

σ_a≃σ(n, γ), (35)

qualunque sia il numero atomico del nucleo considerato. Vi sono però due eccezioni molto importanti alla (35). La prima riguarda i nuclei con Z molto basso che figurano a sinistra delle (33); in questi nuclei, il processo (n, γ) non ha luogo, in quanto l'emissione della particella carica indicata a destra delle (33) stesse è enormemente più rapida dell'emissione di un quanto gamma. Pertanto σ_a si riduce a σ(n, p) nel processo (33a) e a σ(n, α) nei processi (33b) e (33c). L'altra eccezione, molto importante, si ha in alcuni nuclei molto pesanti come il ²³³Th, l'²³⁵U e il ²³⁹Pu; in questi nuclei la fissione è esoenergetica e ha luogo - con caratteristiche in qualche modo simili a quelle del processo (n, γ) - anche per neutroni di bassissima energia. In questo caso la sezione di assorbimento si riduce a

σ_a≃σ(n, γ)+σ_f, (36)

dove σ_f indica la sezione d'urto per fissione.

Nonostante il fatto che la teoria dei singoli nuclei non sia ancor oggi così avanzata e completa come sarebbe desiderabile, si possono dare alcune formule di validità generale che forniscono la dipendenza di σ_sc e σ_a dall'energia cinetica E del neutrone incidente.

Limitandoci, per ragioni di semplicità, a considerare in questa sede solo i processi di assorbimento dei neutroni, si può scrivere in generale

σ_a(E)=π???53???²C(E), (37)

dove C(E) è un numero, funzione di E, che è sempre minore o al massimo uguale a 1. Per neutroni di energia elevata (10-20 MeV) che colpiscono un nucleo pesante, così che si abbia ???53???〈R, questo fattore può essere facilmente calcolato nel caso estremo (non molto lontano dalla realtà, nelle condizioni sopra specificate) in cui il nucleo assorba tutti i neutroni che lo colpiscono. In questo caso la (37) si riduce a

σ_a(E)≃πR², (38)

ossia la sezione d'assorbimento è uguale alla sezione geometrica del nucleo considerato. Nella (38) è scomparsa la lunghezza d'onda del neutrone e l'unica lunghezza che vi figura è il raggio del nucleo.

Ma al diminuire dell'energia del neutrone si raggiungono sempre condizioni tali che ???53???≫R. In queste condizioni conviene porre il fattore C nella forma

e sostituire nella (37):

Questa relazione stabilisce che, se c è costante, o è per lo meno una funzione molto lentamente variabile dell'energia, vale la così detta ‛legge 1/v': la sezione d'urto per assorbimento è inversamente proporzionale alla velocità del neutrone incidente. Il significato di questa legge è evidente se si ricorda la relazione che intercorre fra la probabilità per unità di tempo P_a di un dato processo, nel caso presente la cattura del neutrone, e la corrispondente sezione d'urto: per definizione si ha

P_a=nvσ_a, (41)

dove n è il numero di neutroni di velocità v per centimetro cubico, cosicché nv rappresenta il flusso di neutroni, cioè il numero di neutroni che cadono nell'unità di tempo sull'unità di superficie.

Dalla (41) segue che la legge 1/v significa che P_a è indipendente dall'energia dei neutroni incidenti: qualunque sia la velocità del neutrone esso ha sempre la stessa probabilità di cadere ‛dentro' un nucleo quando gli passa vicino.

L'esperienza ha mostrato che la legge 1/v è effettivamente rispettata assai bene in molti casi entro intervalli di velocità abbastanza estesi. Essa per esempio è rispettata con grande precisione nei processi (33) a partire da energie bassissime (v→0) fino a energie diverse nei diversi processi, ma sempre dell'ordine di 10⁵ eV o maggiori. Tale legge è rispettata anche in molti processi (n, γ) a partire da v→0 fino a energie che possono essere di qualche eV o maggiori.

La legge 1/v era stata suggerita sin dal 1934-1935 da vari autori, in particolare da Fermi, come una legge generale che permetteva di render conto dell'ipotesi b) enunciata all'inizio del cap. 3. Ma già nel corso del 1935 alcuni risultati sperimentali di T. Bjerge e C. H. Westcott (Cambridge, Inghilterra), di B. P. Moon e J. R. Tillman (Londra) e di L. Arsimovitch e collaboratori (Mosca) avevano portato questi autori a dubitare della sua validità generale e a suggerire che la dipendenza di σ_a da E potesse essere diversa da nucleo a nucleo e in qualche modo caratteristica del nucleo considerato. Uno studio sperimentale sistematico eseguito negli anni 1935-1936 da Amaldi e Fermi (Roma) portò a stabilire che σ(n, γ) presenta, praticamente in tutti i nuclei, alcune risonanze, ossia degli stretti intervalli di energia in cui la sezione d'urto di assorbimento varia rapidamente raggiungendo un massimo molto pronunciato (v. Rainwater, 1957; v. Harvey, 1970). Il fenomeno è analogo a quello che si osserva nell'assorbimento della luce da parte di un atomo irraggiato con uno spettro continuo: l'atomo assorbe selettivamente solo la luce dotata di ben determinati valori della lunghezza d'onda, corrispondenti alle sue righe di assorbimento, dando così luogo al fenomeno della risonanza ottica. L'interpretazione del fenomeno, osservato poco dopo anche da altri autori (in particolare O. R. Frisch e collaboratori a Copenhagen), fu data agli inizi del 1936 da N. Bohr (Copenhagen) e da G. Breit e E. Wigner (Princeton, USA) e fu successivamente posta in forma generale da H. Bethe e G. Placzek (Copenhagen, 1936).

Nel caso di un nucleo che abbia una sola risonanza la (37) si riduce alla formula di Breit e Wigner

dove

è un fattore statistico derivante dal fatto che il neutrone incidente può avere lo spin parallelo o antiparallelo allo spin J del nucleo bombardato; E_R è l'energia di risonanza definita come l'energia del neutrone per cui σ_a è massimo e

Γ=Γ_n+Γ_γ (43)

è la larghezza totale della riga, somma delle larghezze per emissione di un quanto gamma e riemissione di un neutrone; queste - divise per ℏ - danno le probabilità per unità di tempo che il nucleo composto, formatosi in seguito alla cattura del neutrone incidente, dia luogo al corrispondente processo di emissione.

Poiché Γ_γ dipende solo molto lentamente dall'energia del neutrone, mentre Γ_n è, con buona approssimazione, inversamente proporzionale a ???53???, allora, per valori di E che siano così piccoli rispetto a E_R da poter essere trascurati nel denominatore, la (42) contiene automaticamente la legge 1/v; questa viene osservata sperimentalmente tutte le volte che in un nucleo la risonanza di energia più bassa è al di sopra della zona di energia studiata e sufficientemente lontana da essa.

Fenomeni di risonanza analoghi, e per gli stessi valori di E_R, si osservano anche per la sezione d'urto elastico σ_sc e quindi anche per la sezione d'urto totale (31). Nella fig. 10 sono riportati i risultati sperimentali relativi a σ_tot nel caso dell'Au, che, nella regione al di sotto di 30 eV, presenta una sola risonanza per E_R=4,91 eV, rappresentata molto bene dalla formula a un solo livello di Breit e Wigner. Per energie nettamente inferiori a E_R si nota l'andamento di σ_tot tipico della legge 1/v.

Nella fig. 11 è dato, oltre alla sezione d'urto σ_tot anche il rapporto σ_sc/σ_a tra la sezione d'urto elastico e quella per assorbimento dell'isotopo ¹¹₄³₈Cd, che viene usato come filtro per l'assorbimento dei neutroni termici (v. sotto, cap. 9).

Nella fig. 12 è data inftne la sezione d'urto per fissione dell'isotopo ²³₉7₃NP (moltiplicata per √-E in modo da eliminare il fattore 1/v); essa mostra in modo particolarmente evidente varie risonanze molto strette.

9. La rivelazione dei neutroni.

I metodi usati per la rivelazione dei neutroni sono molteplici e assai diversi a seconda dell'intervallo di energia in cui si vuole o si deve sperimentare. Nel caso dei neutroni lenti i metodi più frequentemente usati, per la loro alta efficienza, sono due. Il primo è basato sull'impiego di contatori proporzionali contenenti 2³He oppure ¹0₅B allo stato gassoso (trifluoruro di boro: BF₃). Sotto l'azione di un neutrone lento questi nuclei subiscono rispettivamente le reazioni esoenergetiche (33a) e (33c), nelle quali vengono emesse particelle cariche registrabili per mezzo di un contatore. Talvolta il boro, più raramente il litio (v. la reazione 33b), vengono usati allo stato solido disperdendoli, sotto forma metallica o di composto, in polvere molto fine o in strati sottilissimi entro un plastico scintillante. Si ottiene così un contatore a scintillazione che dà un impulso ogniqualvolta un neutrone viene catturato secondo uno dei processi (33c) o (33b).

Il fatto che per neutroni lenti le sezioni d'urto dei processi (33) seguano la legge 1/v costituisce in molti casi un vantaggio assai notevole.

L'altro metodo di rivelazione dei neutroni lenti che viene frequentemente usato è basato sulla radioattività artificiale provocata dai processi (n, γ) in foglie molto sottili, il più delle volte metalliche. In questo caso, la foglia viene esposta per un tempo ben determinato nel punto ove si vuole misurare il flusso dei neutroni, per esempio nell'interno di un reattore. Terminato l'irraggiamento, la foglia viene estratta e posta davanti a un contatore di raggi beta l'attività così misurata è proporzionale al flusso di neutroni cui la foglia è stata esposta. Fra i materiali più frequentemente usati a questo scopo vanno ricordati l'¹⁹⁷Au (T_1/2=2,7 giorni) e l'¹¹⁵In (T_1/2=54 minuti). Questo metodo (detto per attivazione) presenta il grande vantaggio rispetto al precedente che una foglia metallica sottile, con un'area di pochi centimetri quadrati, ha un ingombro molto piccolo e altera quindi assai poco la geometria dei mezzi nelle sue vicinanze. Affinché l'operazione di misura non alteri sensibilmente la distribuzione di neutroni preesistente nelle sue vicinanze è poi necessario che l'assorbimento globale della foglia sia molto piccolo.

La separazione fra i neutroni termici e i cosiddetti neutroni epitermici si ottiene proteggendo il rivelatore - sia esso un contatore a ³He o ¹⁰B, oppure una foglia metallica - con uno schermo di cadmio, il cui isotopo con A=113, attraverso un processo (n, γ), si trasforma nell'isotopo stabile con A=114. Poiché il ¹¹₄³₈Cd ha una forte risonanza a E_R=0,178 eV (v. fig. 11), basta usare uno schermo di cadmio dello spessore di qualche decimo di millimetro perché esso assorba completamente tutti i neutroni di energie al di sotto di 0,4-0,6 eV, mentre lascia passare praticamente indisturbati i neutroni di energia superiore. Ne segue che uno qualunque dei rivelatori di neutroni lenti sopra descritti, schermato con cadmio, rivela solo i neutroni epitermici (cioè quelli di energia superiore a 0,4-0,6 eV) ma non i neutroni termici.

Per determinare sperimentalmente il flusso dei neutroni termici basta fare la differenza fra le indicazioni fornite dal rivelatore adottato quando esso non è schermato e quando è schermato con cadmio (Amaldi e Fermi, 1936; L. Szilard, 1936).

Per energie superiori a qualche decina di eV il metodo per attivazione non può più essere usato, mentre si possono ancora usare i contatori basati sulle reazioni (33) (v. Barschall, 1958). La fig. 13 mostra le sezioni d'urto di questi processi per energie fino a qualche MeV. Come si vede, in questa regione energetica la sezione d'urto di questi processi si è fortemente ridotta rispetto ai corrispondenti valori nelle regioni termica ed epitermica. Ciò comporta una notevole riduzione dell'efficienza di rivelazione, riduzione per altro inevitabile, in quanto, secondo la (37), la massima sezione d'urto per assorbimento è sempre solo una frazione di π???53???² e ???53???² è inversamente proporzionale all'energia del neutrone. Quando, al crescere dell'energia, ???53??? diventa confrontabile o addirittura minore del raggio R del nucleo bombardato, la sezione d'urto di qualunque processo di assorbimento non è più determinata da ???53??? bensì da R (v. in particolare l'eq. 38).

Per energie comprese fra qualche MeV e 20-30 MeV la rivelazione dei neutroni viene fatta per mezzo di altri processi, fra i quali ricordiamo (v. Siegel, 1958) l'urto elastico contro protoni contenuti sotto forma di idrogeno entro un contatore o in strati sottili di materiali idrogenati posti davanti a un singolo contatore oppure a più contatori in coincidenza. Questo metodo in realtà si impiega spesso già per energie al di sotto di 20 MeV.

Un altro processo utilizzato per rivelare i neutroni è la radioattività indotta in vari nuclei da reazioni (n, p), (n, 2n) o (n, α) dotate di una soglia reale, in quanto si tratta di processi endoenergetici, o di una soglia apparente, grazie all'azione della barriera di potenziale (v. sopra, cap. 7).

Per esempio, il processo ¹²C (n, 2n) ¹¹C ha la soglia a 22 MeV e il prodotto della reazione ha una vita media T_1/2=20,4 minuti; mentre il processo ³¹P (n, p) ³¹Si ha una soglia efficace a circa 2 MeV e il prodotto della reazione ha una vita media T_1/2=2,7 h. In questo caso la tecnica di misura è del tutto simile a quella descritta per i neutroni lenti.

L'impiego di un rivelatore la cui soglia E, sia di poco al di sotto della massima energia E_max dei neutroni presenti nello spettro incidente permette di sperimentare su di uno spettro di neutroni che si estende fra E_s ed E_max e che, in condizioni opportune, può essere paragonato a una riga spettrale, anche se invero assai larga.

Vi sono, infine, contatori o camere di ionizzazione contenenti un sottile strato di materiale fissile. In queste condizioni, il contatore registra i frammenti prodotti nella fissione, i quali danno impulsi molto grandi e quindi facilmente separabili da eventuali fondi di altra origine, per esempio raggi gamma.

In alcuni dei nuclidi che vengono usati a tale scopo il processo di fissione ha una soglia piuttosto bassa: per esempio nel ²³¹Pa si ha E_s=0,4 MeV e nell'²³⁸U E_s=1,2 MeV, mentre per altri (²³³U, ²³⁵U, ²³⁹Pu) il processo è esoenergetico e segue, alle bassissime energie, la legge 1/v. La fissione di questi ultimi nuclidi può quindi essere usata anche per la rivelazione dei neutroni lenti. Per neutroni veloci, σ_f è sempre molto prossimo a 1 b, cosicché l'efficienza di questi rivelatori è sempre molto bassa.

Per energie dei neutroni incidenti dell'ordine di 50-100 MeV viene usato talvolta ancora il primo processo, ossia l'urto elastico del neutrone contro i protoni contenuti in un materiale idrogenato. Ma a queste energie, e soprattutto a energie ancora maggiori, si preferisce di solito usare uno scintillatore - solido o liquido - dello spessore di 20 40 cm; un neutrone che colpisca uno qualunque dei nuclei presenti, in gran parte H, C, O, N, dà luogo nel caso dell'idrogeno a un urto elastico, negli altri casi a processi in cui vengono emessi vari corpuscoli, alcuni dei quali sono carichi, altri neutri. I corpuscoli carichi, qualunque sia la loro origine, provocano una scintillazione che viene osservata mediante un fotomoltiplicatore. Con un contatore di questo tipo si possono raggiungere efficienze di circa il 20%. Poiché esso è, tuttavia, sensibile non solo ai neutroni, ma anche a qualsiasi corpuscolo carico che lo attraversi, è necessario proteggerlo con opportuni contatori in anticoincidenza che permettano di eliminare la registrazione delle scintillazioni provocate da ogni corpuscolo carico che incida su di esso dall'esterno.

10. Cenno ad alcuni impieghi dei neutroni.

Come si è detto all'inizio del presente articolo, i neutroni hanno trovato numerose importanti applicazioni nei campi più disparati. Fra queste occupa il primo posto per i suoi aspetti industriali ed economici la costruzione dei reattori nucleari che vengono oggi impiegati, in tutto il mondo, per la produzione di energia termica ed elettrica o per la propulsione navale e, prossimamente, aerea e spaziale. Si è anche accennato al fatto (v. sopra, cap. 7) che oggi si costruiscono reattori nucleari dotati di caratteristiche tali da essere particolarmente adatti per produrre flussi di neutroni termici ed epitermici di elevata intensità. Questi possono essere utilizzati in loco, cioè dentro lo stesso reattore, per produrre considerevoli quantitativi di corpi radioattivi artificiali oppure, attraverso opportuni canali, possono essere portati all'esterno del reattore, anche a distanze notevoli, per impiegarli in ricerche d'interesse scientifico e tecnologico. In questo contesto, l'espressione ‛interesse scientifico' non si riferisce alle ricerche riguardanti le proprietà dei neutroni o la struttura nucleare, alle quali già si è accennato nei capitoli precedenti, ma a ricerche riguardanti altri campi della fisica, come la fisica dei solidi o, più in generale, degli stati aggregati o addirittura lo studio di certi processi chimici e biologici.

Le applicazioni possibili dei neutroni sono tante e di tipo così diverso da non poter essere elencate, e tanto meno illustrate, nei limiti del presente articolo. Ci si limiterà quindi ad accennare solo ad alcune di esse, escludendo a priori qualsiasi cenno agli impieghi dei radioisotopi. Tra questi, per esempio, figura la tecnica dei ‛traccianti', che ha reso possibili molti fra i più importanti progressi fatti dalla farmacologia e dalla biologia moderna negli ultimi venti o trent'anni. La loro esclusione è suggerita dal fatto che si tratta di applicazioni per così dire indirette dei neutroni; ma non si può dimenticare che esse sarebbero state impossibili se la fisica dei neutroni non avesse raggiunto il livello attuale.

Come esempio di applicazione d'interesse tecnologico, e non solo tecnologico, si può scegliere la ‛radiografia neutronica' o ‛neutronigrafia'. Questa è una tecnica di analisi non distruttiva mediante la quale è possibile ottenere, su emulsione fotografica o su altro materiale sensibile, le immagini geometriche di oggetti vari attraversati da un fascio di neutroni, ben paralleli, di conveniente energia. Di solito, si fa uso dei neutroni lenti forniti da un reattore di ricerca o da altra sorgente (v. sopra, cap. 7). Dopo aver attraversato l'oggetto in esame, i neutroni colpiscono un convertitore, il quale può essere del tipo indiretto o diretto. Un convertitore indiretto è costituito da una lastra d'oro, d'indio o di disprosio, dello spessore di qualche decimo di millimetro, in cui i neutroni lenti producono, attraverso un processo (n, γ) di elevata sezione d'urto, isotopi radioattivi. L'attività prodotta in ogni punto del convertitore è proporzionale all'intensità del fascio neutronico trasmessa, cosicché, dopo un'esposizione di opportuna durata, si ottiene una vera e propria immagine radioattiva. Tale immagine viene quindi trasferita, lontano dal fascio di neutroni, su una pellicola fotografica particolarmente sensibile ai raggi beta, con cui il convertitore viene mantenuto in contatto per un tempo opportuno. In tal modo, la presenza dei raggi gamma, che spesso accompagnano i neutroni, non dà luogo ad alcun inconveniente. In assenza di raggi gamma, può convenire l'uso di un convertitore diretto, costituito da uno scintillatore per neutroni del tipo ⁶LiF+ZnS(Ag) (in cui si sfrutta la reazione 33b), che, durante l'esposizione al fascio di neutroni, è mantenuto a contatto con la pellicola fotografica.

La neutronigrafia non è equivalente alle solite radiografie con raggi X o gamma per la seguente ragione. Queste ultime radiazioni, una volta fissata la loro energia, hanno un coefficiente di assorbimento che è una funzione crescente e regolare del numero atomico Z; in particolare, esse sono assorbite assai poco dall'idrogeno o da altri elementi leggeri. Il coefficiente di assorbimento dei neutroni, invece, essendo determinato dalla corrispondente σ_tot non è legato in modo semplice nè al numero atomico nè al numero di massa dei diversi nuclidi e varia al variare dell'energia in modo piuttosto irregolare e molto diverso non solo da elemento a elemento, ma anche da isotopo a isotopo. Pertanto, scegliendo opportunamente l'energia dei neutroni o ripetendo la neutronigrafia successivamente per diverse energie, è possibile analizzare la struttura di un oggetto in un modo del tutto nuovo. Per esempio si possono ottenere neutronigrafie, dotate di notevole contrasto, di materiali idrogenati contornati da altri materiali aventi una struttura cristallina come il ferro. Con neutroni di energia pari a 0,003 eV, ossia molto lenti o ‛freddi', come si dice, il ferro è quasi trasparente, mentre l'idrogeno assorbe notevolmente: la sezione d'urto totale dei neutroni di questa energia è, infatti, rispettivamente σ_tot≃10 b e σ_tot≃90 b. La lunghezza d'onda dei neutroni è, inoltre, così grande da non dar luogo nei cristallini di ferro ai fenomeni di diffrazione di cui si parlerà fra poco.

Se si usano, invece di neutroni termici, neutroni dotati dell'energia di risonanza di un particolare nuclide, si possono ottenere neutronigrafie che mettono in evidenza, con notevole contrasto, aspetti strutturali particolari di certi oggetti o materiali. In fig. 14 son poste a confronto una radiografia convenzionale (A) e una neutronigrafia (B) ottenuta con un generatore del tipo scaled-off tube contornato da un moderatore di polietilene. Si tratta della valvola di ritegno per gasolio, il cui corpo di ottone contiene una molla d'acciaio e un tappo di nylon. L'esposizione a un flusso integrato di 5×10⁶ neutroni/cm² è durata 500 secondi. Si noti come la neutronigrafia metta in evidenza il corpo centrale mobile di nylon [C₁₂H₂₂N₂O₂]_n.

Un altro importante impiego dei neutroni si ha nello studio delle strutture molecolari di corpi liquidi o gassosi e soprattutto di corpi cristallini, attraverso i fenomeni di diffrazione cui danno luogo. Nel seguito ci si limiterà alla diffrazione dei neutroni lenti da parte dei cristalli, messa in evidenza per la prima volta da P. Preiswerk e H. von Halban (Parigi, 1936). Essa è qualitativamente simile alla diffrazione dei raggi X, nel senso che, quando un fascetto ben collimato dell'una o dell'altra di queste radiazioni incide sulla superficie di un cristallo sotto una direzione che formi un angolo ϑ con i piani riflettenti del reticolo, si osserva un massimo dell'intensità della radiazione riflessa solo per quei valori di ϑ che soddisfano la condizione di Bragg (v. fig. 15):

mλ=2d sen ϑ, (44)

dove λ è la lunghezza d'onda della radiazione, m è un numero intero positivo, detto ‛ordine di riflessione', e d è la distanza fra i piani reticolari in oggetto. Poiché d è dell'ordine di qualche ängström, per poter osservare questo fenomeno per valori di ϑ non troppo scomodi da misurare, è necessario che anche λ sia dello stesso ordine di grandezza. Come si vede dalla (8), questa condizione è soddisfatta, per esempio, da neutroni di energia kT, con T corrispondente circa alla temperatura ambiente. Ponendo in quella relazione E=0,025 eV (vedi eq. 5a), si ha infatti

λ=1,81 Å. (45)

La diffrazione dei neutroni lenti differisce tuttavia da quella dei raggi X o degli elettroni per vari aspetti molto importanti. L'onda elettromagnetica dei raggi X, quando si propaga attraverso la materia, viene diffusa (o, come si dirà nel seguito, sparpagliata) quasi interamente dagli elettroni, così che la sezione d'urto fotone-atomo è una funzione crescente regolare del corrispondente numero atomico Z. Poiché gli elettroni sono distribuiti entro tutto il volume dell'atomo, le cui dimensioni lineari sono confrontabili con la lunghezza d'onda dei raggi X incidenti, si hanno fenomeni d'interferenza fra le onde sparpagliate dai diversi elementi di volume dell'atomo stesso. Ne segue una diminuzione dell'intensità della radiazione sparpagliata al crescere dell'angolo di sparpagliamento, di cui si tiene conto introducendo il fattore di forma atomico. Considerazioni del tutto analoghe valgono nel caso delle onde di de Broglie relative a elettroni di energia tale da avere una lunghezza d'onda confrontabile con le lunghezze interatomiche. In questo caso, l'onda incidente è sparpagliata sia dagli elettroni dell'atomo, sia dal suo nucleo, in quanto l'elettrone incidente interagisce con gli uni e con l'altro mediante le forze coulombiane che dipendono solo da Z.

Nel caso delle onde di de Broglie relative al moto dei neutroni lenti che si propagano in un materiale non magnetico, la situazione, come si chiarirà fra poco, è completamente diversa: a) lo sparpagliamento da parte di un atomo nel mezzo è dovuto solo all'interazione del neutrone con il nucleo e tale interazione non è legata in modo semplice al numero atomico Z o al numero di massa A del nucleo stesso. Questo ha dimensioni piccolissime rispetto alla lunghezza d'onda dei neutroni e pertanto non si hanno i fenomeni d'interferenza a cui s'è accennato sopra nel caso dei raggi X o degli elettroni; ne segue che lo sparpagliamento subito dai neutroni da parte di un singolo atomo è isotropo, ossia non dipende dall'angolo di sparpagliamento; b) quando la radiazione neutronica è sparpagliata da un insieme di atomi disposti in maniera regolare, come si verifica nel caso di una molecola o in modo ancor più evidente nel caso di un cristallo, e si osservano i fenomeni d'interferenza a cui essa dà luogo, si nota che solo una parte delle onde sparpagliate sono coerenti e concorrono quindi all'interferenza. La parte incoerente è dovuta alle vibrazioni termiche degli atomi attorno alle loro posizioni d'equilibrio, alla presenza di isotopi di uno stesso elemento chimico distribuiti a caso, che sparpagliano i neutroni in modo diverso l'uno dall'altro, e all'orientamento disordinato degli spins nucleari rispetto agli spins dei neutroni incidenti. A seconda del nuclide considerato, la parte coerente della radiazione neutronica viene sparpagliata senza cambiamento di fase o con un cambiamento di fase di 180° rispetto all'onda neutronica incidente. Anche sotto questo aspetto, dunque, i neutroni mostrano un comportamento diverso da quello dei raggi X, per i quali non si ha sfasamento fra onda incidente e onda sparpagliata.

Da queste brevi osservazioni appare chiaro che la diffrazione dei neutroni può fornire, in generale, informazioni diverse da quelle che si deducono dalla diffrazione dei raggi X o degli elettroni da parte dello stesso cristallo. A differenza di quella dei raggi X, essa permette, per esempio, di localizzare gli atomi di idrogeno disposti in un cristallo fra atomi di elevato Z oppure di distinguere nuclidi dotati di numeri atomici molto vicini nella stessa matrice cristallografica o di raffinare la conoscenza delle strutture di liquidi o solidi amorfi e così via.

Ma, a parte queste osservazioni di carattere generale, esistono due fenomeni specifici per i quali la diffrazione dei neutroni lenti costituisce l'unico mezzo di osservazione e misura oggi a disposizione: si tratta dei fenomeni in cui intervengono, rispettivamente, le proprietà magnetiche e le proprietà dinamiche dei cristalli. Per lo studio di questi fenomeni si usano spettrometri a tre assi (v. fig. 16): una prima riflessione serve a produrre il fascio monoenergetico e, se necessario, polarizzato; la seconda riflessione ha luogo sul campione da studiare; la terza, infine, permette l'analisi della quantità di moto e dell'energia dei neutroni sparpagliati dal campione.

Le proprietà magnetiche di un materiale cristallino possono essere studiate mediante la diffrazione dei neutroni lenti, in quanto essi sono dotati di un momento magnetico (v. tab. I): quando un'onda neutronica si propaga in un mezzo, essa subisce, oltre allo sparpagliamento da parte dei nuclei, di cui si è parlato fino a ora, anche uno sparpagliamento magnetico dovuto all'interazione degli eventuali momenti magnetici atomici con quello del neutrone. Ma poiché i momenti magnetici degli atomi provengono, in massima parte, dai momenti magnetici associati agli spins degli elettroni, l'interazione magnetica avviene in una regione le cui dimensioni sono dello stesso ordine della lunghezza d'onda del neutrone incidente. Pertanto, lo sparpagliamento magnetico, a differenza di quello nucleare, non è isotropo, ma dipende dall'angolo di sparpagliamento, secondo una legge determinata dal fattore di forma magnetico, che è una proprietà caratteristica del tipo di atomo considerato.

La sezione d'urto differenziale dσ_sc/dΩ per sparpagliamento elastico coerente contro gli atomi di un materiale ferromagnetico viene così a dipendere sia dall'angolo di sparpagliamento che dall'angolo fra la direzione dello spin del neutrone incidente e la direzione di magnetizzazione del cristallo. In particolare, essa è molto diversa a seconda che lo spin dei neutroni, che è antiparallelo al momento magnetico, risulti parallelo o antiparallelo alla direzione di magnetizzazione del materiale attraversato. Questo fenomeno, previsto da F. Bloch nel 1936 (Stanford, Stati Uniti), si esprime quantitativamente mediante la seguente formula della sezione d'urto neutrone-atomo magnetizzato:

dove b rappresenta il contributo all'ampiezza sparpagliata avente origine dall'urto nucleare e p il contributo dovuto all'interazione magnetica. Nella (46) si deve usare il segno + o il segno − a seconda che i neutroni incidenti siano polarizzati parallelamente o antiparallelamente alla direzione di magnetizzazione degli atomi del materiale attraversato.

Diventa così possibile produrre dei fasci di neutroni lenti polarizzati con i quali si possono fare molte esperienze interessanti, in particolare le esperienze di diffrazione da parte di cristalli. Misurando l'intensità di uno dei massimi di Bragg (v. equazione 44) con neutroni polarizzati una volta parallelamente e una volta antiparallelamente alla direzione di magnetizzazione di un cristallo, si determina l'ampiezza dell'onda sparpagliata per interazione magnetica in quella particolare riflessione e si elimina così automaticamente il fondo dovuto allo sparpagliamento incoerente.

Mediante l'uso di neutroni polarizzati è stato così possibile misurare i momenti magnetici degli atomi nelle leghe ferromagnetiche, i fattori di forma magnetici degli elementi di transizione, nonché studiare le sostanze antiferromagnetiche, la struttura dei domini e così via.

Fasci di neutroni monocromatici altamente polarizzati si ottengono per riflessione alla Bragg di neutroni termici provenienti da un reattore sul piano (200) di un cristallo di magnetite (Fe₃O₄) o, ancor meglio, sul piano (111) della lega Co 92% Fe 8%. In entrambi questi casi, i due termini b e p che figurano nella (46) sono all'incirca eguali fra loro, cosicché lo sparpagliamento coerente ha luogo praticamente solo per i neutroni polarizzati parallelamente alla direzione di magnetizzazione del cristallo monocromatore.

Come esempio dei risultati che si possono ottenere con questo metodo, nella fig. 17 è mostrata la distribuzione della densità di magnetizzazione nel gadolinio. Per studiare questo elemento ferromagnetico, i ricercatori del laboratorio di Oak Ridge si sono serviti di cristalli singoli arricchiti al 99,993% dell'isotopo ¹⁶⁰Gd, dotato, a differenza degli altri isotopi di questo stesso elemento, di una sezione d'urto di cattura molto piccola. In questo, come in altri elementi ferromagnetici, la densità di magnetizzazione è la somma della densità locale, dovuta agli elettroni 4f, e di una densità diffusa dovuta agli elettroni di conduzione disaccoppiati. Il secondo contributo è particolarmente sensibile nelle regioni lontane dagli atomi. Le linee mostrate in figura indicano il luogo dei punti in cui la magnetizzazione è nulla; nell'interno delle figure la densità è negativa.

Lo studio delle proprietà dinamiche dei cristalli riguarda la seguente categoria di fenomeni. Come è noto, gli atomi di un corpo solido, mantenuto a una certa temperatura, compiono dei moti oscillatori attorno alle loro posizioni di equilibrio, dovuti all'agitazione termica. Nel caso di un cristallo tali moti sono il risultato della sovrapposizione di un gran numero di ‛modi' di oscillazione che, essendo quantizzati, vengono indicati con il nome di ‛fononi'. Ciascun fonone corrisponde a un'onda sinusoidale di frequenza ν_f, che si propaga nella direzione del vettore di propagazione q, il cui modulo è pari all'inverso della lunghezza d'onda del fonone:

Conoscere la dinamica del cristallo comporta la conoscenza della relazione di dispersione, ossia della relazione

ν_f=ν_fj(q), (47)

per tutti i valori dell'indice j. Nel caso di reticoli monoatomici, j individua i diversi stati di polarizzazione dei fononi, mentre nel caso di reticoli più complessi esso indica, oltre la polarizzazione, anche altri caratteri dei fononi. Ora, come è stato mostrato per via teorica da G. Placzeck e L. Van Hove (Princeton, SUA, 1954), lo sparpagliamento anelastico dei neutroni lenti monocromatici da parte di un cristallo permette di determinare le relazioni di dispersione (47). Senza entrare nei dettagli della teoria, basti notare che, quando un fascio di neutroni di energia molto bassa incide su di un cristallo, si possono osservare oltre ai massimi alla Bragg (v. equazione 44) dovuti allo sparpagliamento elastico dei neutroni, ossia a uno sparpagliamento senza scambio di energia fra neutroni e cristallo, anche dei neutroni che hanno subito urti anelastici, ossia urti in cui essi hanno perso energia per l'eccitazione di uno o, raramente, più fononi del cristallo oppure hanno acquistato l'energia ceduta loro da un fonone del cristallo. Tali urti, naturalmente, hanno luogo rispettando la conservazione dell'energia e della quantità di moto. Queste leggi si esprimono mediante delle relazioni del tipo:

dove E e p, E′ e p′ sono l'energia cinetica e la quantità di moto, rispettivamente, del neutrone incidente e del neutrone diffuso, hν_f e q individuano il fonone scambiato e τ è un vettore che rappresenta il contributo del cristallo alla conservazione della quantità di moto (τ è un vettore del reticolo reciproco del cristallo). Poiche τ è noto una volta fissate le condizioni in cui avviene la riflessione da parte del cristallo, E e p sono noti ed E′ e p′ vengono misurati, le (48) permettono di conoscere direttamente i valori delle due grandezze hν_f e q che figurano nella relazione di dispersione (47).

Anche nel caso dello sparpagliamento anelastico bisogna distinguere fra sparpagliamento coerente e incoerente; quanto si è detto sopra riguarda naturalmente solo lo sparpagliamento coerente. Ci si può ora domandare quale sia la ragione per cui questo tipo di ricerche si può fare coi neutroni lenti e non, per esempio, coi raggi X. La risposta è da ricercare nella diversa relazione che intercorre fra energia e lunghezza d'onda per questi due tipi di radiazione. Come si vede dalla (45), per avere una lunghezza d'onda pari a 1,81 Å, bisogna usare neutroni di 0,025 eV, ossia neutroni di energia confrontabile con l'energia di gran parte dei fononi del cristallo. Il trasferimento dell'energia di un fonone dal cristallo a un neutrone, o viceversa, dà luogo a un cambiamento assai notevole dell'energia del neutrone. Per avere la stessa lunghezza d'onda, ossia λ≃1,81 Å, nel caso dei raggi X bisogna usare fotoni di energia

ossia fotoni di energia cosi elevata che una variazione di qualche decimo di eV, quali sono quelle determinate da processi di scambio di fononi con il cristallo, non è in alcun modo osservabile.

Nella fig. 18 sono mostrati, a titolo di esempio, i risultati ottenuti nel caso del cloruro di cesio da un gruppo dell'Oak Ridge National Laboratory (Stati Uniti).

Con questi metodi, tuttora in via di sviluppo, è stato possibile misurare le relazioni di dispersione (47) di numerosi cristalli e così conoscere una delle proprietà più fini e fondamentali dei corpi allo stato cristallino. La tendenza attuale sembra rivolta principalmente allo studio della struttura dinamica dei cristalli molecolari e delle leghe metalliche.

Bibliografia.

Amaldi, E., The production and slowing down of neutrons, in Handbuch der Physik (a cura di S. Flügge, vol. XXXVIII, 2, Berlin 1959, pp. 1-659.

Barschall, H. H., Detection of neutrons, in Handbuch der Physik (a cura di S. Flügge), vol. XLV, Berlin 1958, pp. 437-486.

Bartoli, B., Felicetti, F., Silvestrini, V., Electromagnetic structure of the hadrons, in ‟La rivista del nuovo cimento", 1972, II, p. 241.

Beckurts, K. H., Wirtz, K., Neutron physics, Berlin 1964.

Egelstaff, P. A., Poole, M. J. (a cura di), Experimental neutron thermalization, London 1969.

Fermi, E., Note e memorie. Collected papers, vol. I, Roma 1962, vol. II, Roma 1965.

Gurevich, J. I., Tarasov, L.V., Low energy neutron physics, Amsterdam 1968.

Harvey, J. A. (a cura di), Experimental neutron resonance spectroscopy, New York 1970.

Hughes, D. J., Reactor techniques, in Handbuch der Physik (a cura di S. Flügge), vol. XLIV, Berlin 1959, pp. 390-446.

IAEA (International Atomic Energy Agency), Neutron inelastic scattering, 4 voll., Wien 1965-1968.

Marion, J. B., Fowler, J. L., Fast neutron physics, New York 1960.

Phillips, G. C., Marion, J. B., Risser, J. R., Progress in fast neutron physics, Chicago 1963.

Rainwater, J., Resonance processes by neutrons, in Handbuch der Physik (a cura di S. Flügge), vol. XL, Berlin 1957, pp. 373-474.

Ringo, G. R., Neutron diffraction and interference, in Handbuch der Physik (a cura di S. Flügge), vol. XXXII, Berlin 1957, pp. 552-641.

Shull, C. G., Wollan, E. O., Applications of neutron diffraction to solid state problems, in Solid state physics (a cura di F. Seitz e D. Turnbull), vol. II, New York 1956, pp. 137-217.

Siegel, R. T., High energy neutron detectors, in Handbuch de Physik (a cura di S. Flügge), vol. XLV, Berlin 1958, pp. 487-517.