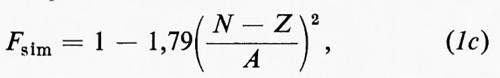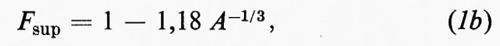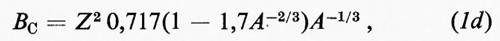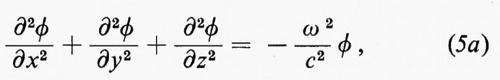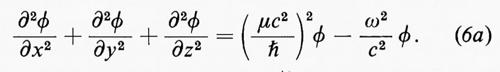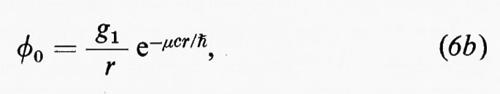Nuclei atomici

Nuclei atomici

Struttura dei nuclei, di Hans A. Bethe e Philip J. Siemens

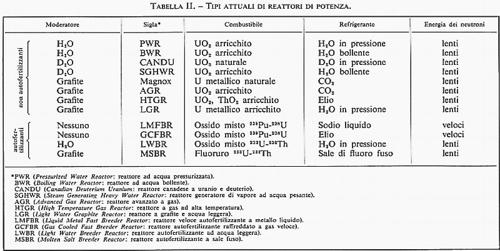
Reattori nucleari, di Lothar W. Nordheim e Alvin M. Weinberg

Armi nucleari, di J. Carson Mark

Struttura dei nuclei

SOMMARIO 1 Introduzione. □ 2. Proprietà dei nuclei. □ 3. Forze nucleari ed energia di legame. □ 4. Il modello a guscio. □ 5. Stati collettivi. □ 6. Collisioni nucleari. □ 7. Disintegrazione beta. □ 8. Fissione. □ 9. Fusione. □ Bibliografia.

1. Introduzione.

Il nucleo atomico fu scoperto nel 1911 da lord E. Rutherford, il quale trovò che una piccola percentuale degli ioni di elio che urtavano ad alta velocità una lamina d'oro era soggetta a forze di violenza tale da invertire la direzione del moto delle particelle. Per spiegare le sue osservazioni, Rutherford fece l'ipotesi che dovessero esservi delle concentrazioni di carica e di massa in regioni aventi un diametro non superiore a 2 × 10^-12 cm all'interno dell'atomo di oro, che ha un diametro di 3 × 10^-8 cm. Così Rutherford rappresentò l'atomo come formato da un nucleo con carica positiva che occupa un volume piccolo, ma in cui è contenuta quasi tutta la massa dell'atomo, circondato da elettroni attratti dal campo elettrico della carica positiva. Poco tempo dopo, la teoria quantistica di N. H. D. Bohr sul moto degli elettroni in un campo centrale permise di dimostrare che le righe di lunghezza d'onda più corta nello spettro della luce emessa da un atomo hanno lunghezze d'onda inversamente proporzionali al quadrato della carica del nucleo. Questa carica risultò essere pari a un multiplo intero, Z, della carica dell'elettrone e, di modo che un atomo neutro ha Z elettroni all'esterno del nucleo. Tutti gli atomi di uno stesso elemento chimico hanno la stessa carica nucleare Ze, la quale differisce però da elemento a elemento. Quando, poi, misure compiute con lo spettrografo di massa, da poco inventato, mostrarono che la maggior parte degli elementi chimici sono delle mescolanze di due o più tipi di atomi chimicamente identici, che hanno la stessa carica nucleare Ze ma massa leggermente differente, divenne chiaro che questa carica era una proprietà chimica ben più importante del peso atomico. Ad atomi dello stesso elemento, ma con peso diverso, fu dato il nome di ‛isotopi'. Le masse di questi isotopi (all'infuori di quelle degli isotopi dell'idrogeno) non differiscono di più dello 0,1% da multipli interi di una singola ‛unità di massa' (per es., un dodicesimo della massa della più abbondante specie di atomo di carbonio è quasi perfettamente uguale a un sedicesimo della massa del più comune tipo di atomo di ossigeno). Questa scoperta indusse i fisici a riesumare le idee di W. Prout, che già nel 1815 aveva suggerito che gli elementi più pesanti fossero costituiti a partire da atomi di idrogeno.

L'idea che tutti i nuclei si potessero formare a partire da quello dell'idrogeno, o protone, non rendeva da sola ragione del valore intero delle masse e delle cariche nucleari. Per esempio, la massa di un normale atomo di azoto è quattordici volte maggiore di quella del protone, mentre la sua carica è di solo sette volte maggiore di quella del protone. Così, il nucleo di azoto consiste di sette protoni e di sette particelle di uguale massa, ma senza carica, chiamate neutroni. Al pari degli elettroni di un atomo, i protoni e i neutroni di un nucleo sono caratterizzati, nella teoria quantistica, da onde di una certa lunghezza d'onda λ. Nel diametro nucleare d deve esserci abbastanza spazio per almeno mezza lunghezza d'onda. Ma, per la relazione di de Broglie, una particella di lunghezza d'onda λ si muove con una quantità di moto p = 2πℏ/λ, dove ℏ indica la costante di Planck divisa per 2π. Di conseguenza i neutroni e i protoni di un nucleo di azoto si muovono a una velocità almeno pari a quella che avrebbero se fossero stati accelerati da un potenziale elettrico di dieci milioni di volt (si dice che essi hanno un'energia di 10 MeV, cioè di 10 milioni di elettronvolt). Ovviamente devono esserci delle forze molto intense tra neutroni e protoni che impediscono loro di staccarsi gli uni dagli altri: uno dei principali obiettivi della fisica nucleare è proprio quello di comprendere queste forze.

L'esistenza di forze non elettriche tra particelle nucleari fu sfruttata, nei primi esperimenti, per osservare il comportamento del neutrone fuori dal nucleo. Per prima cosa era necessario ‛persuadere' un nucleo a separarsi da uno dei suoi neutroni. Quando un nucleo pesante o una particella nucleare ad alta velocità urtano contro un nucleo, questo spesso reagisce emettendo, in un tempo brevissimo (generalmente di circa 10^-20 secondi), una o più delle particelle che lo costituiscono. J. Chadwick e F. e J. Joliot-Curie diressero dei nuclei di elio ad alta velocità contro un bersaglio di berillio e osservarono che esso emetteva neutroni. Essi accertarono la presenza dei neutroni attraverso lo studio delle ulteriori reazioni da questi causate quando giungevano all'apparecchio di rivelazione e furono in grado di mostrare che la massa del neutrone è all'incirca uguale a quella del protone.

Un neutrone, lasciato a se stesso, si trasforma, dopo una vita media di circa 1.000 secondi, in un protone, un elettrone e un neutrino; lo stesso processo, o quello corrispondente in cui viene emesso un elettrone positivo, può anche aver luogo all'interno di un nucleo, anche se più velocemente o più lentamente che per un neutrone isolato. Tuttavia l'esistenza di questi processi di ‛decadimento beta' non sta a indicare che un neutrone consista di un protone più un elettrone e un neutrino, o che i nuclei siano composti di protoni e di elettroni. Piuttosto, il lungo tempo richiesto per i processi di decadimento beta, in confronto ai 10^-20 secondi necessari per una reazione nucleare tra protoni e neutroni, indica che il decadimento beta non comporta soltanto la separazione di due particelle legate l'una all'altra, ma anche un cambiamento molto più drastico nella costituzione della materia (v. sotto, cap. 7). I fisici nucleari considerano i neutroni particelle elementari alla stessa stregua dei protoni. Invero, secondo un suggerimento di W. K. Heisenberg, queste possono quasi sempre essere considerate come due forme della stessa particella, avendo, fatta eccezione per le proprietà elettriche del protone, quasi le stesse proprietà e gli stessi tipi di interazione all'interno dei nuclei. I fisici nucleari hanno introdotto la parola ‛nucleone' per indicare sia i neutroni sia i protoni.

Il fatto che un neutrone possa trasformarsi in un protone e viceversa non ha praticamente alcun effetto sulla struttura dei nuclei. Esso, tuttavia, spiega perché non si trovino in natura tutti i nuclei possibili (per es., quello costituito da 2 protoni e 4 neutroni): questi possono trasformarsi in altri nuclei più strettamente legati mediante l'emissione di un elettrone (la cosiddetta particella beta). Anche se in alcuni casi il tempo di questa reazione è di qualche anno, è passato un tempo sufficientemente lungo dalla formazione della Terra perché, salvo poche eccezioni, qualsiasi quantità di tali nuclei, che poteva una volta esistere, sia da molto tempo scomparsa.

2. Proprietà dei nuclei.

Attualmente, la fisica nucleare studia sia i modi in cui i protoni e i neutroni possono formare degli aggregati, sia le proprietà più salienti di questi ultimi, come il numero di neutroni e di protoni che contengono, l'energia con cui sono legati insieme, la dimensione e la forma dei nuclei che ne risultano. Nel trattare di una determinata specie di nucleo, si suole indicare con la lettera Z il numero di protoni che esso contiene, con N il numero di neutroni, con A il numero totale di nucleoni (per cui A = N + Z) e con B l'energia con cui sono legati insieme. Z viene detto ‛numero atomico' e A 'numero di massa'.

Di tutti gli infiniti modi in cui si può immaginare di combinare assieme varie quantità di neutroni e di protoni, in natura si trovano soltanto circa 300 combinazioni, rappresentate nella fig. 1; inoltre ne sono state prodotte in laboratorio altre duemila circa, alcune delle quali potrebbero anche trovarsi in certe stelle. Queste combinazioni di N e di Z sono quelle più strettamente legate insieme; tutte le altre sono instabili, cioè trovano presto un modo per tra- sformarsi in una delle configurazioni più strettamente legate. Di conseguenza, per ogni numero di protoni Z, c'è un numero di neutroni N preferito. Nuclei con un certo valore di Z e con un numero di neutroni molto inferiore ( o superiore) a quello preferito N decadranno con un processo beta trasformando protoni in neutroni (o viceversa) con l'emissione di elettroni positivi (o negativi) fino a raggiungere la relazione tra N e Z preferita. La fig. 1 mostra chiaramente questa relazione e anche il fatto che non esistono nuclei naturali con più di 238 nucleoni. Questo accade perché aggregati così grandi si spezzano rapidamente, a causa della forte repulsione elettrica tra i protoni, in due o più nuclei di minori dimensioni. Questo processo di rottura, chiamato ‛fissione', può anche aversi, in circostanze favorevoli, in elementi più leggeri (v. cap. 8).

Se si costruisse un nucleo riunendo insieme il numero necessario di neutroni e di protoni, verrebbe emessa una gran quantità di energia dovuta alle intense forze tra i nucleoni, proprio come accade quando l'acqua, cadendo sotto l'influenza dell'attrazione gravitazionale della Terra, libera energia in una stazione idroelettrica. L'energia totale, B(N, Z), che verrebbe liberata nella costruzione di un nucleo con N neutroni e Z protoni vielle chiamata ‛energia di legame' e può essere misurata in vari modi: per esempio, si può Costruire un nucleo in diversi stadi, aggiungendo un protone o un neutrone (o magari due o quattro) alla volta e misurando l'energia liberata ogni volta, e poi sommando alla fine tutte le energie liberate a ogni stadio per trovare l'energia totale liberata.

L'energia B liberata quando neutroni e protoni si combinano per formare un nucleo porta via con sé una certa massa m, secondo la relazione di Einstein B = mc², dove c indica la velocità della luce. Di conseguenza, un nucleo con energia di legame B è più leggero della somma delle masse delle particelle che lo costituiscono di una quantità m = B/c², che per la maggior parte dei nuclei è pari a circa lo 0,8% della massa totale. Quindi da una misura precisa della massa di un nucleo se ne può dedurre l'energia di legame. In uno spettrografo di massa gli ioni vengono accelerati fino a raggiungere una certa energia cinetica e vengono poi deviati da un campo magnetico. Gli ioni pesanti vengono deviati meno di quelli leggeri e perciò una misura precisa della deviazione può fornire un valore accurato della massa degli ioni e quindi anche dell'energia di legame. Con gli spettrografi di massa si sono potute misurare le masse nucleari con una precisione di una parte su 10⁸. Il fatto che le energie di legame misurate con lo spettrografo di massa siano perfettamente in accordo con le misure delle energie liberate nelle reazioni in cui i nuclei vengono sintetizzati dai loro elementi costitutivi rappresenta un'importante verifica della teoria della relatività speciale di Einstein e anche dell'accuratezza degli esperimenti.

Le differenze tra l'energia di legame di due specie nucleari possono anche essere dedotte dalle misure dell'energia degli elettroni emessi nel decadimento beta. L'energia liberata nel decadimento beta si ripartisce tra l'elettrone e il neutrino, che vengono emessi allo stesso tempo. Il neutrino, che è una particella con massa di riposo nulla che praticamente non interagisce con niente, è assai difficile da osservare: ogni tanto, però, l'elettrone si porta via quasi tutta l'energia liberata. Osservando, quindi, molti elettroni di decadimento beta provenienti dallo stesso processo, è possibile vedere quanta energia possiederebbe l'elettrone se il neutrino non ne avesse alcuna. Nel calcolare l'energia totale liberata in un decadimento beta è importante tener conto dell'energia rappresentata dalla massa di riposo dell'elettrone oltre che della differenza di massa tra protone e neutrone.

Le energie di legame B di tutte le specie nucleari stabili sono quasi esattamente proporzionali al numero di nucleoni che compongono il nucleo, il che significa che l'energia di legame media per particella, B/A, è quasi uguale per tutti i nuclei, a eccezione di quelli più leggeri. Nella fig. 2 è riportata, per ogni A, l'energia di legame per particella del nucleo stabile osservato. Le energie di legame osservate seguono abbastanza da vicino la cosiddetta formula a ‛goccia liquida':

B^GL = 15,68 F_sup F_sim A - B_C, (1a)

in cui:

ove B^GL e B_C s'intendono misurate in MeV.

La parte principale dell'energia di legame B è proporzionale al numero di nucleoni A, come è suggerito dall'analogia con l'energia di una goccia di liquido. Ogni particella riceve uguale beneficio dalla presenza delle altre, a eccezione di quelle che si trovano sulla superficie della goccia. La frazione di nucleoni vicini alla superficie del nucleo è più piccola per i nuclei grossi, essendo proporzionale ad A^-1/3; per tener conto di ciò viene introdotto nell'equazione (1a) il fattore F_sup. Il secondo fattore F_sim viene introdotto perché l'energia di legame si riduce nel caso in cui non vi sia un numero uguale di neutroni e di protoni, cioè quando (N-Z) non sia uguale a zero. Per le forze nucleari non v'è distinzione tra neutroni e protoni, ma poiché esse sono maggiori quando vi sia un egual numero di questi e di quelli, il prezzo che si deve pagare per avere N diverso da Z deve essere almeno proporzionale a (N-Z)². Questa regola, naturalmente, non governa la repulsione elettrica tra i protoni, di cui tiene conto l'ultimo termine B_C. Le costanti dell'equazione (1a) possono essere approssimativamente ricavate dalla conoscenza delle forze tra nucleoni, ma possono essere determinate con precisione molto maggiore se vengono scelte in modo da riprodurre le misure delle energie di legame. Per questa ragione, si dice che l'equazione (1a) è ‛semiempirica'.

La formula (1a) predice, per un dato numero totale A di nucleoni, una dipendenza quadratica dell'energia di legame dal numero di protoni Z, con un legame massimo di Z eguale ad A/2 per A piccolo, ma inferiore ad A/2 per i nuclei più pesanti. I nuclei il cui valore di Z è diverso dall'optimum dovrebbero trasformarsi, attraverso un processo di decadimento beta, in un nucleo il cui Z è il numero intero più vicino al valore ottimale. In tal modo, la formula (1a) spiega la corrispondenza che si osserva tra i valori di Z e di N per nuclei beta-stabili (v. fig. 1). Inoltre, le energie di legame dei nuclei che hanno il medesimo A dipendono effettivamente in maniera parabolica da Z, ma ciò si verifica soltanto per i nuclei con un numero totale A di particelle dispari (v. fig. 3).

Su un diagramma che rappresenti B in funzione di Z vi sono due parabole per i nuclei con A pari (v. fig. 3B): i massimi si hanno per lo stesso valore di Z, coerentemente con l'equazione (1a), ma le energie di legame per i nuclei i cui N e Z sono ambedue dispari sono minori di quelle che si hanno per i nuclei con N e Z pari. Questo effetto pari-dispari si riscontra per molti valori diversi di A, di modo che la formula semiempirica di massa dell'equazione (la) deve essere corretta con un termine

B^P = 41[1 − δ(N) − δ(Z)]A^1/2, (2)

dove δ(N) e δ(Z) sono eguali a 1 o a 0, a seconda che N e Z siano rispettivamente dispari o pari e B^P si intende ancora misurata in MeV. Si dice che questo termine è dovuto ad ‛appaiamento', un effetto che sarà di nuovo trattato nel cap. 4.

Quando al termine B^GL si aggiunge B^P, la formula semiempirica di massa diviene un'ottima approssimazione dell'energia di legame osservata sperimentalmente per i nuclei con più di dieci nucleoni. La differenza tra l'energia di legame B dello stato fondamentale misurata e l'energia semiempirica totale B^GL + B^P viene detta ‛energia di guscio':

S(N, Z) = B(N, Z) − (B^GL + B^P). (3)

Questa differenza S(N, Z), riportata nella fig. 4, è particolarmente grande per i nuclei con N o Z pari a 8, 20, 28, 50, 82 o 126, ciò che sta a indicare come i nuclei con questi numeri di neutroni e protoni siano legati in maniera particolarmente stretta. Questi nuclei posseggono anche altre proprietà speciali: per esempio, sono tutti di forma sferica. L'esistenza di questi numeri ‛magici' è rimasta a lungo un fatto inspiegabile, ma ora può essere capita mediante il modello a guscio (v. cap. 4).

L'analisi delle reazioni nucleari ha mostrato che vi possono essere molte strutture nucleari diverse con lo stesso numero N di neutroni e Z di protoni, ma che esiste sempre una di queste strutture che è legata più strettamente delle altre. Un nucleo che possegga una qualunque delle altre strutture decade rapidamente in quella più favorevole, liberando di solito energia sotto forma di quanti di luce. La struttura più favorevole che può essere costruita con N neutroni e Z protoni si chiama ‛stato fondamentale' del nucleo AZ. Qualsiasi altra struttura che sia meno favorevole dello stato fondamentale si chiama invece ‛stato eccitato' del nucleo AZ e la differenza tra la sua energia di legame e quella dello stato fondamentale prende il nome di ‛energia di eccitazione'. La differenza tra le energie di legame di due stati nucleari può essere determinata osservando una reazione nucleare in cui uno degli stati viene prodotto dall'altro e misurando sia l'energia cinetica della particella che dà inizio alla reazione, sia quella di tutti i prodotti della reazione (eventualmente anche l'energia dei quanti di luce emessi). L'energia netta prodotta, o assorbita, è uguale alla differenza tra l'energia di legame dello stato nucleare prodotto e quella del nucleo originale. L'osservazione delle energie di eccitazione e delle altre proprietà degli stati eccitati ha contribuito notevolmente alle nostre conoscenze sulla struttura non soltanto delle configurazioni nucleari eccitate, ma anche dello stato fondamentale. Per esempio, una delle proprietà caratteristiche dei nuclei con numeri magici di neutroni e di protoni è la mancanza di stati eccitati a bassa energia di eccitazione.

Si può studiare il modo in cui neutroni e protoni sono distribuiti all'interno di un nucleo osservando come vengono deviate o assorbite delle particelle nucleari veloci quando urtano un nucleo. L'unità di lunghezza usata in fisica nucleare è il ‛fermi', abbreviato in F, che è uguale a 10^-13 cm. Le forze nucleari non si estendono a una distanza maggiore di circa 2 F; entro questo raggio però esse sono molto intense, di modo che, quando un neutrone veloce arriva a una distanza di circa 2 F da uno dei neutroni o protoni del nucleo, esso sarà fortemente deviato - fors'anche si potrà unire al nucleo stesso - mentre, se passa a una distanza maggiore, non subirà alcuna influenza. Il numero di neutroni deviati o assorbiti quando un fascio di neutroni attraversa uno spessore sottile di materia sarà proporzionale all'area che ogni nucleo presenta di profilo e che viene detta ‛sezione d'urto' del nucleo. Le misure mostrano che i raggi nucleari variano in maniera regolare al variare di A, da circa 2 F per l'elemento più leggero, l'elio, a circa 8 F per quello più pesante, l'uranio. La precisione di queste misure è tuttavia severamente limitata dalla natura complessa delle forze interagenti tra i nucleoni, che rende difficile l'interpretazione delle misure delle sezioni d'urto.

Misure relative alla distribuzione dei protoni, ma non dei neutroni, interpretabili in modo più sicuro e preciso, si possono ottenere mediante l'uso di elettroni o di mesoni μ i quali interagiscono con i nucleoni soltanto attraverso le forze elettriche. La forza elettrica è semplice e ben conosciuta, così che è possibile fare il ragionamento inverso, partendo dalle misure sperimentali delle deviazioni degli elettroni per arrivare alla distribuzione delle cariche del nucleo. Elettroni ad alta velocità - e quindi con una piccola lunghezza d'onda di de Broglie - possono rivelare anche dei dettagli assai fini della distribuzione delle cariche. Per esempio, degli elettroni accelerati da un potenziale di 750 milioni di volt hanno una lunghezza d'onda di de Broglie di 1,7 F. Onde di lunghezza λ sentono delle variazioni nella distribuzione della carica entro distanze un po' minori di λ, all'incirca fino a

???53??? = λ/2π = ℏ/p. (4)

Quindi elettroni di 750 MeV sono sensibili a variazioni nella distribuzione di cariche che abbiano luogo entro distanze di circa 0,3 F.

Queste misure di diffusione degli elettroni possono essere integrate con l'osservazione delle interazioni dei mesoni μ con i nuclei. Un mesone M è molto simile a un elettrone, ma ha una massa circa 200 volte più grande: di conseguenza un mesone μ che faccia parte di un atomo sarà 200 volte più vicino al nucleo atomico di quanto non lo sia un elettrone. Un mesone μ in un atomo può anche passare buona parte del suo tempo dentro al nucleo, dove il suo moto sarà sensibile ai campi elettrici all'interno del nucleo. Lo studio di tali atomi fornisce dunque delle informazioni sulla distribuzione di carica all'interno del nucleo, che rappresentano un'utile integrazione delle misure di diffusione di elettroni.

Le misure fatte con gli elettroni e i mesoni μ mostrano che tutti i nuclei, a eccezione dei più leggeri (con A 16), hanno una regione centrale di densità quasi uniforme ρ₀ = 0,16 nucleoni F^-3, circondata da una pellicola abbastanza sottile in cui la densità scende da 0,9ρ₀ a 0,1ρ₀ entro una distanza di 2,4 F (v. fig. 5).

In tal modo, ciascun nucleo rassomiglia a una goccia di liquido con volume e superficie abbastanza ben definiti. Il volume è proporzionale al numero di nucleoni A e, poiché i nuclei sono all'incirca sferici, i loro raggi sono proporzionali ad A^1/3. Molti nuclei non sono perfettamente sferici, ma un po' oblunghi: anzi non è raro che un nucleo abbia la forma di un ellissoide di lunghezza doppia della larghezza. Alcuni nuclei sono rotondi, in particolare quelli in cui N e Z sono ambedue numeri magici, mentre i nuclei i cui N e Z stanno a metà strada tra due numeri magici consecutivi sono di solito i più oblunghi; vi sono addirittura alcuni nuclei che sono un po' appiattiti. Tali deformazioni non sferiche producono, nella regione attorno al nucleo, campi elettrici a simmetria non sferica che possono essere sentiti dagli elettroni dell'atomo che stanno intorno al nucleo oppure rivelati con altri metodi. La misura di questi campi elettrici cosiddetti di ‛multipolo' dà un'indicazione abbastanza diretta della distorsione nella distribuzione della carica nucleare.

Molti nuclei producono anche campi magnetici la cui intensità si misura mediante una grandezza detta ‛momento magnetico' del nucleo. Questo è in parte dovuto al moto dei protoni all'interno del nucleo: poiché i protoni sono elettricamente carichi, il loro moto produce una corrente elettrica che dà origine a un campo magnetico. Inoltre, ogni protone e ogni neutrone possiedono un loro momento magnetico intrinseco che contribuisce al campo magnetico del nucleo. Con tutte queste possibili sorgenti di magnetismo ci si potrebbe aspettare che i nuclei grossi abbiano momenti magnetici molto grandi, ma si è invece visto che gli stati fondamentali dei nuclei con N e Z pari hanno momento magnetico nullo, mentre quelli con N e Z dispari hanno quasi tutti un momento magnetico che non supera quello che potrebbe esser prodotto da una sola particella. Così, apparentemente, il campo magnetico creato da ogni particella viene annullato da quello di un'altra. Per ogni particella che si muove dentro il nucleo in una direzione ve n'è un'altra che ruota in senso opposto, con il campo intrinseco invertito. Una simile conclusione sulla rotazione e sull'orientazione dei nucleoni può essere raggiunta attraverso lo studio del momento angolare totale di varie specie nucleari. Sebbene i nuclei siano composti di molti nucleoni che si muovono rapidamente nell'interno del nucleo stesso e sebbene ci siano prove evidenti del fatto che ogni nucleone ha un momento angolare piuttosto grande, il momento magnetico angolare totale di un nucleo non è praticamente mai più grande di quello di uno soltanto dei nucleoni che lo compongono: evidentemente l'effetto dei moti dei diversi nucleoni si annulla globalmente. La spiegazione di questa straordinaria caratteristica della struttura nucleare costituisce un ulteriore successo del modello a guscio (v. cap. 4).

3. Forze nucleari ed energia di legame.

Le forze che tengono insieme un nucleo possono essere misurate o mediante lo studio delle interazioni tra nucleoni all'interno di nuclei grandi e complessi, oppure, più semplicemente, mediante lo studio delle interazioni tra due o tre nucleoni. Una terza possibilità consiste nel cercare di dedurre tali forze dalla costituzione dei singoli nucleoni e delle loro possibili subunità, come per esempio i mesoni π. Quest'ultima sarebbe la possibilità ottimale; poiché è anche la più difficile da realizzare, è stata attuata soltanto in parte. Finora l'informazione più dettagliata sulle forze nucleari è stata ottenuta mediante esperienze condotte con sistemi di due o tre nucleoni, benché gli altri due metodi di studio abbiano anch'essi fornito delle conoscenze essenziali.

Lo strumento principale per lo studio delle forze intercorrenti tra nucleoni è la deflessione, o ‛diffusione', di fasci di neutroni o di protoni da parte dei protoni di un bersaglio costituito da atomi di idrogeno. Il numero delle particelle deviate ad angoli diversi dipende dalle forze cui sono soggette le particelle del fascio quando passano vicino ai protoni del bersaglio. Fasci di particelle di differenti energie possono fornire indicazioni diverse sulla forza. Per esempio, i neutroni che si prelevano dai reattori nucleari hanno energie fino a qualche MeV e quindi lunghezze d'onda di de Broglie maggiori di 10 F: di consegnenza sono sensibili soltanto alle caratteristiche più salienti della forza nucleare, cioè alla sua intensità, alla distanza fin cui si fa sentire e alla sua dipendenza dalle direzioni dei momenti angolari intrinseci, o spins, dei due nucleoni al momento dell'urto. Invero, tutti i risultati sulla diffusione neutrone-protone e protone-protone con fasci di energia minore di 20 MeV si possono interpretare mediante il solo uso di due parametri, chiamati ‛lunghezza di diffusione' e ‛raggio efficace', ognuno dei quali dipende dall'orientazione degli spins dei due nucleoni.

Per acquisire delle conoscenze più dettagliate, specialmente rignardo a quello che accade ai nucleoni quando si avvicinano molto gli uni agli altri, è necessario impiegare fasci di particelle con lunghezza d'onda di de Broglie più corta. Fasci di questo tipo possono essere prodotti solo mediante l'impiego di acceleratori speciali, come l'acceleratore lineare e il sincrociclotrone, in cui si tiene conto dei cambiamenti di massa dei nucleoni veloci quando la loro velocità si avvicina a quella della luce, laddove i ciclotroni ordinari sono regolati sulla massa della particella accelerata. Tutti questi sistemi utilizzano i campi elettrici per accelerare le particelle e possono dunque essere adoperati solamente per particelle cariche. Invece fasci di neutroni di elevata energia si possono produrre soltanto mediante delle reazioni nucleari che siano state iniziate da particelle cariche di alta energia: i fasci ottenuti contengono neutroni di energia variabile e sono molto meno intensi dei fasci di protoni ottenuti direttamente dagli acceleratori, di modo che è difficilissimo fare delle esperienze precise con dei fasci di neutroni. La cosa è ulteriormente complicata dalla necessità di misurare la dipendenza dell'interazione dalla direzione degli spins delle particelle. In pratica questo si fa osservando i processi in cui il neutrone o il protone viene deviato due o addirittura tre volte e questo perché nè gli acceleratori nè gli strumenti di rivelazione sono in grado di distinguere la direzione degli spins dei nucleoni. Tuttavia si può sfruttare il caso di una collisione nucleare in cui la deviazione dei nucleoni dipenda dalla direzione dei loro spins per scegliere dei nucleoni con lo spin orientato secondo una direzione particolare e per dirigerli poi contro un bersaglio in cui gli spins nucleari siano stati allineati con l'aiuto di campi magnetici. La dipendenza dell'interazione dallo spin fa sì che percentuali diverse di nucleoni siano diffuse ad angoli differenti rispetto allo spin dei nucleoni (v. fig. 6).

I risultati degli esperimenti di diffusione possono essere meglio analizzati in termini di una serie di parametri chiamati ‛sfasamenti', i quali dipendono dall'energia e dal momento della quantità di moto delle particelle del fascio. Nella fisica classica il momento della quantità di moto ℒ dei nucleoni è uguale al prodotto vettoriale della quantità di moto p del moto relativo e della loro distanza di separazione r : ℒ = r × p (v. fig. 7). La direzione di ℒ è perpendicolare a r e a p e il suo modulo è uguale al prodotto del modulo di p per la distanza relativa b alla quale passerebbero le due particelle se proseguissero lungo una traiettoria rettilinea. Nella teoria quantistica questo momento delìa quantità di moto può assumere valori determinati: ℒ = √-l-(-l- -+- -1-) ℏ, dove I = 0, 1, 2, ecc. Per ogni l ci sono quattro combinazioni dei momenti di spin dei due nucleoni, che normalmente si distinguono in termini del momento della quantità di moto totale dello spin, S = √-s-(-s- -+- -1-) ℏ e della somma vettoriale di S e di ℒ indicata con ℱ = √-j-(-j- -+- -1-) ℏ (v. fig. 8). La deviazione delle particelle con dati l, s e j può essere analizzata mediante una grandezza detta sfasamento δ_lsj(E) che dipende soltanto dall'energia E della particella diffusa. Come indicato dal nome, lo sfasamento misura la differenza tra la fase dell'onda di de Broglie, rappresentante le particelle con un dato momento di quantità di moto che si avvicinano al bersaglio, e quella dell'onda rappresentante le particelle che se ne allontanano. Uno sfasamento eguale a zero sta a indicare che le particelle sono passate senza essere disturbate, uno sfasamento positivo indica che sono state attratte dai nucleoni del bersaglio e uno negativo che sono state respinte. Nelle figg. 9, A e B, sono mostrati alcuni esempi degli sfasamenti ottenuti in misure di diffusione di nucleoni di diverse energie, nelle quali sono stati eliminati gli effetti dovuti alla forza elettrica tra protoni. Gli sfasamenti sono massimi per l = 0 e decrescono rapidamente per l più grande, perché le particelle con un momento della quantità di moto grande non si avvicinano mai abbastanza da risentire delle forze nucleari. Le particelle con l maggiore di 6 o 7 non sono praticamente deviate se la loro energia è minore di circa 300 MeV. Sono stati compiuti anche degli esperimenti di diffusione con fasci di energia maggiore, ma essi non si possono descrivere semplicemente alla stregua di collisioni tra due nucleoni perché spesso danno luogo alla produzione di mesoni π.

Mentre, in teoria, gli sfasamenti possono essere determinati univocamente dagli esperimenti di diffusione, in pratica, a causa della precisione limitata e della difficoltà delle esperienze di diffusione tripla, si è in grado di spiegare le misure di diffusione entro i limiti della precisione sperimentale, con parecchi insiemi diversi di sfasamenti δ_lsj. Tra queste alternative, se ne può scegliere una, mostrata nelle figg. 9 e 10, che è in accordo con quelle previsioni della teoria mesonica che sono ritenute le più attendibili. Dalla fig. 10 si rileva l'importanza della dipendenza dell'interazione nucleare dagli spins dei nucleoni: se le forze non dipendessero dagli spins, i tre sfasamenti sarebbero uguali. La dipendenza della forza dallo spin, illustrata nella fig. 10, viene chiamata interazione di spin-orbita. Un'altra componente della forza, chiamata interazione tensoriale, è in grado di cambiare l'orientazione del momento angolare di spin dei nucleoni, accoppiandolo al momento angolare del loro moto relativo. La fig. 10D mostra un parametro che misura l'intensità di questa interazione per le particelle con l = 0 prima e dopo che esse comincino a interagire.

Dalle figg. 9 e 10 si rileva anche che la forza nucleare è assai diversa per diffusioni con momenti l della quantità di moto diversi: essa è in media leggermente repulsiva se l è dispari, ma attrattiva se l è pari (questa caratteristica fu invero dedotta per la prima volta dalle proprietà dei nuclei pesanti, nel 1933, ossia molto prima che fossero tecnicamente realizzabili gli esperimenti di diffusione). Si può dimostrare che una forza di questo tipo, chiamata ‛forza di scambio', può nascere da mesoni π.

Sebbene l'interazione nucleare tra nucleoni dipenda fortemente dal momento angolare relativo e dall'orientazione degli spins, essa è quasi indipendente dalla carica che portano i nucleoni. (Per il principio di esclusione di Pauli, gli stati quantici possibili per il sistema neutrone-protone sono di più che per due particelle uguali. L'indipendenza delle forze dalla carica si riferisce soltanto agli stati accessibili sia alle particelle uguali, sia a quelle diverse). Così, introdotte le opportune correzioni per le forze elettromagnetiche, si vede che gli sfasamenti relativi all'urto neutroneprotone e protone-protone non differiscono che per poche parti su cento. Non è possibile controllare con precisione, in una collisione tra due nucleoni, l'ipotesi chiamata di ‛indipendenza dalla carica', secondo la quale le forze tra due protoni, tra un neutrone e un protone o tra due neutroni sono uguali, perché è praticamente impossibile far urtare due neutroni. È più facile controllare le conseguenze che l'ipotesi dell'indipendenza dalla carica avrebbe per la struttura dei nuclei complessi, perché in nuclei diversi con Z differente ma con il medesimo A (gli stati ‛analoghi isobarici' del cap. 4) si dovrebbero trovare degli stati con la stessa struttura. Le piccole differenze che si osservano nella struttura di questi stati possono dipendere da differenze di circa il 3% nelle forze tra tipi diversi di nuclei. Un'ipotesi meno plausibile, detta della ‛simmetria della carica', consisterebbe nell'ammettere che la forza nucleare è uguale per coppie di particelle uguali, cioè nel caso di due neutroni o di due protoni, diversa per particelle diverse, cioè nel caso di un neutrone e un protone. Sembra che ci siano delle deviazioni di circa il 3% per le forze tra due neutroni e tra due protoni.

Un modo conveniente per rappresentare le forze nucleari si può ottenere tracciando un grafico dell'energia potenziale V_lsj(r) di due nucleoni a varie distanze relative r. Questa energia potenziale V_lsj,(r) non descrive in modo completo l'andamento delle forze nucleari, le quali dipendono anche dalla velocità relativa dei due nucleoni, nè d'altra parte può essere specificata in maniera univoca dalla misura degli sfasamenti, che si può ottenere solo per lunghezze d'onda di de Broglie maggiori di circa 2 F. Alle informazioni ricavabili dai processi di diffusione si aggiunge quella ottenuta dalle proprietà del deutone, cioè del nucleo dell'idrogeno pesante, composto da un neutrone e da un protone. La forma del deutone è particolarmente sensibile alla componente a più lungo raggio della forza tensoriale, la quale ha un ruolo importante anche nella struttura dei nuclei più pesanti. Sono stati proposti vari andamenti per l'energia potenziale, capaci di spiegare i dati di cui si dispone sull'interazione di due nuclei. Queste curve di potenziale, che sono tra loro assai simili, mostrano tutte che i nucleoni con i pari si attraggono a distanze superiori a circa 0,7 F, ma si respingono fortemente a distanze inferiori (v. fig. 11). L'intensità della repulsione a distanze brevi non è determinata accuratamente dagli esperimenti di diffusione poiché la lunghezza d'onda di de Broglie è troppo grande.

H. Yukawa, nel 1935, fu il primo a suggerire che le forze tra nucleoni potessero dipendere dallo scambio di quanti dotati di massa, chiamati ‛mesoni', in maniera simile a quella in cui la forza elettrica tra due particelle cariche può essere spiegata sulla base di un trasferimento di quanti di luce di massa nulla, ossia di fotoni. Il potenziale elettrico 40 di un'onda elettromagnetica in una regione in cui non vi siano cariche obbedisce all'equazione:

in cui ω è la frequenza angolare dell'onda. Oltre a soluzioni che rappresentano onde che si propagano con velocità c, l'equazione (5a) possiede anche una soluzione ϕ₀ di frequenza zero (ω = 0), che è il potenziale elettrostatico dovuto alla carica q₁,

ϕ₀ = q₁/r (5b)

L'energia potenziale di una carica q₂ posta a una distanza r dalla prima è eguale a V = q₁q₂/r = ϕ₀q₂.

Yukawa suggerì che il potenziale del campo attorno a un nucleone obbedisse, eccetto che nel punto x = y = z = 0, dove si trova il nucleone, all'equazione delle onde:

Le soluzioni ondulatorie dell'equazione (6a) per ciascuna frequenza hanno una lunghezza d'onda ???53??? = [ω²/c² − (μc²/ℏ)²]^-1/2. Se queste onde sono onde di de Broglie, esse rappresentano delle particelle dotate di energia E = ℏω e quantità di moto p = ℏ/λ = (E²/c² − μ²c²)^1/2, che, nella teoria della relatività, rappresenta la quantità di moto di una particella di massa μ ed energia E. Una particella di questo tipo si chiama ‛mesone π'. L'equazione (6a) possiede anche delle soluzioni statiche (ω = 0), che corrispondono al potenziale mesonico a una distanza r dal nucleone

dove g₁ è una costante corrispondente alla carica elettrica q che descrive l'intensità della forza. In tal modo l'energia potenziale di un altro nucleone la cui costante di forza sia g₂ sarà data da

Il potenziale dell'equazione (6c), detto potenziale di Yukawa, decresce rapidamente per distanze superiori a una distanza R tale che μcR = ℏ, cioè per

R = ℏ/μc.

Quindi il raggio d'azione della forza è tanto più corto quanto più è pesante il mesone. L'equazione (6a) presenta anche delle altre soluzioni che non sono a simmetria sferica, ma che descrivono anch'esse delle forze rapidamente decrescenti per distanze maggiori di R.

In natura esistono vari mesoni differenti che contribuiscono alla forza esistente tra due nucleoni, i più leggeri dei quali sono i mesoni π, che hanno una massa pari a circa 138 MeV/c² e che perciò danno luogo a una forza che si estende fino a una distanza R = 1,4 F. Vi sono tre tipi di mesoni π con carica elettrica +e, O e −e; le costanti di forza g₁ e g₂ per ogni mesone dipendono dalle cariche e dagli spins dei nucleoni in modo tale che la somma dei potenziali che essi producono è indipendente dalla carica. Un mesone π non ha spin, ma non ha neanche simmetria sferica e per questo motivo anche il suo campo attorno al nucleone è asimmetrico, il che dà origine a un potenziale leggermente più complicato che dipende dalla direzione degli spins dei nucleoni e include una componente tensoriale. Il raggio d'azione, l'intensità, la dipendenza dal momento della quantità di moto orbitale e di spin della componente a più lungo raggio della forza nucleare possono essere tutti spiegati mediante le proprietà, sperimentalmente determinate, dei mesoni π. Anzi, molte delle proprietà dei mesoni π erano state previste assai prima che un mesone π fosse stato osservato fuori da un nucleo, proprio partendo dalla conoscenza delle forze nucleari. Altri mesoni che contribuiscono alle forze nucleari sono i mesoni ρ e ω, i quali hanno una massa circa cinque volte e mezzo più grande di quella dei mesoni π e quindi sono ritenuti responsabili delle intense forze repulsive che insorgono quando due nuclei si avvicinano molto l'uno all'altro. A tali brevi distanze è anche probabile che le forze nucleari siano sensibili alla struttura dinamica del nucleone i cui effetti appaiono come ‛stati eccitati' di un neutrone o di un protone singolarmente. A distanze intermedie è possibile che i nucleoni interagiscano per mezzo dello scambio simultaneo di due o più mesoni π, aumentando quindi la forza che li attrae e che è di gran lunga troppo grande per essere interpretata come la forza dovuta allo scambio di un solo mesone, quale si osserva nei casi di grandi distanze. Si spera che tutti i vari mesoni, insieme alla struttura dinamica del nucleone, possano dare una spiegazione delle forze osservate tra i nucleoni, però ancora non è stato fatto un calcolo attendibile delle forze nucleari che tenga conto simultaneamente di tutti gli effetti conosciuti (v. particelle elementari).

Avendo chiarito molte cose sulle forze nucleari nei sistemi formati da due soli nucleoni, è interessante vedere come le proprietà dei nuclei complessi siano legate alle forze esistenti tra coppie di nucleoni. Per fortuna, sebbene le forze nucleari siano molto intense per distanze inferiori a 1 F, la distanza media tra i nucleoni di un nucleo è di circa 2 F e quindi, se due nucleoni sono abbastanza vicini per esercitare delle forze molto intense l'uno sull'altro, è assai poco probabile che vi sia un terzo nucleone, anch'esso a distanza sufficientemente piccola, che eserciti una forza intensa su di essi. Questo fatto è alla base delle teorie nucleari ‛a molti corpi' che prendono tutte le mosse dall'ipotesi che all'interno di un nucleo i nucleoni interagiscano essenzialmente a due a due.

Una delle più semplici teorie nucleari a molti corpi è quella di Moskowski e Scott, la quale si basa anche sul fatto che, per gli spins e i momenti delle quantità di moto più importanti, la forza nucleare ha componenti sia attrattive, sia repulsive. Perciò, quando due nucleoni si urtano, essi sono soggetti a una forza repulsiva a piccole distanze e a una forza attrattiva a distanze grandi. C'è una certa distanza d alla quale gli effetti dei potenziali attrattivi e repulsivi si elidono completamente. Il risultato della collisione è uguale a quello che si avrebbe se l'energia potenziale d'interazione fosse zero per distanze minori di d. La distanza d dipende dalla velocità con cui i due nucleoni si urtano: per le velocità dei nucleoni all'interno dei nuclei, d è compreso tra 0,8 e 1,1 F. Al di là di questa distanza, l'energia potenziale d'interazione è minore dell'energia cinetica dei nucleoni, di modo che le onde di de Broglie di questi non sono molto diverse da quelle che sarebbero in assenza d'interazioni, il che rende possibile trovare delle approssimazioni semplici degli effetti dell'interazione. Quando i nucleoni si avvicinano a una distanza minore di d le forze sono intense, ma l'effetto della presenza degli altri nucleoni all'interno del nucleo è piccolo e si può quindi calcolare con metodi semplici di approssimazione. Purtroppo l'utilità della teoria di Moskowski e Scott è limitata perchè essa non tiene conto delle forze tensoriali che sono importanti nei nuclei.

Una teoria capace di trattare qualsiasi tipo di forza, purchè la distanza media tra i nucleoni sia maggiore del raggio d'azione della forza, è quella di Brueckner e Goldstone, che tiene conto del principio di esclusione di Pauli, secondo il quale non possono mai esserci due nucleoni dello stesso tipo nello stesso stato quantico. Nello stato fondamentale di un nucleo con A nucleoni, questi si trovano negli A stati quantici di minore energia. Se due nucleoni si urtano all'interno di un nucleo, dopo la collisione essi devono ritornare al loro stato quantico originario perché gli unici altri stati disponibili richiederebbero più energia di quanta essi non ne abbiano. Di conseguenza le forze nucleari possono perturbare le onde di de Broglie dei nucleoni solo quando questi sono molto vicini e anche in questo caso i cambiamenti sono limitati a quegli stati quantici ad alta energia che non sono occupati da altri nucleoni. La forza nucleare, quindi, disturba il moto dei nucleoni per non più del 15% e questa perturbazione normalmente avviene quando due nucleoni sono a una distanza relativa inferiore a 1 F. La teoria di Brueckner e Goldstone fornisce il modo per calcolare l'entità della variazione delle onde di de Broglie di due nucleoni, dovuta alla forza esistente tra loro, prendendo in considerazione il modo in cui gli altri nucleoni influenzano gli stati quantici disponibili. Si calcola quindi approssimativamente l'effetto di minore importanza dovuto alle collisioni simultanee tra tre o quattro particelle e si trova che esso è responsabile di circa il 10% dell'energia potenziale totale del nucleo.

La teoria nucleare a molti corpi è stata studiata più a fondo nel caso ipotetico della ‛materia nucleare', cioè di un nucleo infinitamente grande senza forze elettriche, in cui le equazioni sono molto più facili da risolvere che nel caso di nuclei reali. L'energia di legame per particella di un tale nucleo dovrebbe essere circa uguale alla costante E₀ = 15,7 MeV che appare nella formula a goccia liquida dell'equazione (la). Inoltre l'energia di legame per particella dovrebbe essere massima per la materia nucleare a densità ‛di saturazione', che è uguale pressappoco alla densità dei nucleoni al centro dei nuclei: ρ₀ = 0,17 nucleoni/F³. Per esempio, i calcoli che partono dal potenziale a due corpi di Reid, riportato nella fig. 11, danno un'energia di legame per nucleone di circa 15 MeV, a una densità di saturazione, però, che è di circa il 30% più grande di ρ₀. Per altre forze che descrivono altrettanto bene la diffusione a due corpi si trova un'energia di legame perfino doppia per densità di saturazione pari a tre volte ρ₀ oppure un'energia di legame più bassa per una densità di saturazione più piccola.

Questa variazione è un risultato delle restrizioni poste dal principio di esclusione di Pauli al moto dei nucleoni all'interno dei nuclei, che rendono l'energia di legame e la densità centrale dei nuclei più sensibili a certe caratteristiche della forza nucleare di quanto non lo siano gli sfasamenti della diffusione. Queste caratteristiche critiche sono l'intensità della forza tensoriale, alla quale sono relativamente insensibili gli esperimenti di diffusione e che questi quindi non possono determinare con precisione, e l'intensità del potenziale repulsivo che entra in gioco quando i nucleoni si avvicinano a distanze inferiori a circa 0,7 F gli uni dagli altri. Gli effetti repulsivi osservati negli sfasamenti di diffusione possono essere in parte dovuti all'indebolimento delle forze di attrazione tra particelle che si muovono velocemente, le quali non sarebbero rinforzate dalla presenza di altri nucleoni come avviene per il caso di un potenziale repulsivo a corto raggio. In questo modo, le proprietà dei nuclei forniscono delle informazioni ulteriori sulla forza nucleare, quali non possono essere desunte dalla diffusione a due neutroni. Le dimensioni conosciute dei nuclei non possono probabilmente essere spiegate ipotizzando una minore forza di repulsione a corto raggio o una componente tensoriale minore di quella riportata nella fig. 11.

4. Il modello a guscio.

La teoria nucleare a molti corpi ha mostrato che, sebbene alle forze che agiscono tra due soli nucleoni alla volta si debba il 90% dell'energia potenziale di un nucleo, ogni collisione che avvenga tra due nucleoni all'interno di un nucleo ha scarso effetto sul moto delle particelle che si urtano. Perciò il moto di ogni nucleone è il risultato medio dell'interazione con molti altri nucleoni. La somma di queste numerose interazioni può essere approssimativamente rappresentata dall'energia potenziale media di un nucleone per effetto degli altri. Questa è massima per un nucleone che si trovi al centro di un nucleo e minima per uno che si trovi vicino ai bordi, dove vi sono meno nucleoni che lo attraggono. L'energia potenziale può anche dipendere dalla velocità del nucleone e dall'orientazione del suo spin. Tale potenziale medio può essere ricavato, con l'aiuto della teoria nucleare a molti corpi, dalla forza che agisce tra due nucleoni: l'esistenza, però, di tale potenziale e le sue proprietà più importanti erano state già dedotte da alcune caratteristiche salienti della struttura nucleare prima ancora che fosse conosciuta la teoria a molti corpi. Nel 1949 Mayer e Jensen, Haxel e Suess mostrarono come sia i numeri magici (v. sopra, cap. 1) sia i momenti delle quantità di moto degli stati fondamentali dei nuclei potessero essere facilmente spiegati mediante il moto dei nucleoni in tale potenziale. Due anni dopo, Bohr e Mottelson mostrarono come anche le forme dei nuclei potessero essere spiegate prendendo in considerazione il fatto che il moto di ciascun nucleone non solo è determinato dal potenziale prodotto dagli altri, ma contribuisce a sua volta a determinare il potenziale in cui si muovono gli altri nucleoni. Gli effetti della struttura nucleare che possono essere compresi semplicemente postulando l'esistenza e definendo le proprietà del potenziale medio senza approfondirne l'origine vengono chiamati effetti del ‛modello a guscio'. Gli effetti, invece, per comprendere i quali è necessaria un'analisi del modo in cui il moto delle particelle influenza il potenziale medio, sono detti effetti ‛collettivi': di questi tratteremo nel cap. 5.

Sebbene la gran parte dei nuclei sia di forma oblunga, molti dei più importanti effetti del ‛modello a guscio' possono essere illustrati considerando nuclei sferici o quasi sferici. Di conseguenza, l'energia potenziale media di un nucleone in posizione r, indicata con V (r), è a simmetria sferica e cioè dipende dalla distanza r = ∣r∣ del nucleone dal centro del nucleo, ma non dalla direzione di r. Il moto quantico di una particella in un potenziale sferico di questo tipo è ben noto. Come nella fisica classica, la relazione tra il moto angolare e quello radiale della particella è determinata dal fatto che il momento ℒ della sua quantità di moto rimane costante. In meccanica quantistica ℒ può assumere soltanto certi valori ℒ = √-l-(-l-+-1-) ℏ dove l = 0, 1, 2, ecc. Questa condizione quantistica è conseguenza del fatto che l'onda di de Broglie che rappresenta il moto angolare deve contenere un numero intero l di lunghezze d'onda per ogni rivoluzione intorno al centro. Per ogni valore di l ci sono 2l + 1 onde differenti che corrispondono a varie orientazioni del moto angolare nello spazio. Una volta specificato il momento l, si risolve l'equazione per il moto radiale tenendo conto della forza centrifuga derivante dal moto angolare. Anche il moto radiale è quantizzato, perché l'onda che lo rappresenta deve contenere un numero intero di mezze lunghezze d'onda tra il centro del nucleo e il suo bordo. Il numero di mezze lunghezze d'onda nel moto radiale è indicato con n = 1, 2, 3, ecc.

Quindi, l'onda associata a una particella che si trovi in un potenziale a simmetria sferica si muove in uno degli stati quantici la cui onda ha l oscillazioni nella direzione angolare ed n semioscillazioni in quella radiale. Ognuno di questi stati quantici rappresenta un moto con una particolare energia E(n,l), che dipende sia dai numeri quantici radiali,sia da quelli angolari. I 2l + 1 stati quantici coi medesimi n ed i hanno la stessa energia perché in essi è diversa soltanto l'orientazione del moto angolare. Un tale gruppo di 2l + 1 stati con la stessa energia E viene chiamato ‛sottoguscio'. Se ci sono vari sottogusci con energie E(n, l) quasi uguali, il raggruppamento viene denominato ‛guscio maggiore'. Nella fig. 12 sono riportati due esempi di potenziale a simmetria sferica in cui si hanno gusci maggiori: il potenziale dell'oscillatore armonico (v. fig. 12A)

V^OA(r) = V₀ + ½kr² (7a)

e il potenziale di Woods-Saxon (v. fig. 12B)

V^WS(r) = V₀/(l + e^(r-R)/a). (7b)

Le energie E(n,l) dei loro stati quantici (n,l) sono riportate nella fig. 13 insieme al numero degli stati quantici diversi aventi la medesima energia (per ognuna delle 2l + 1 orientazioni del moto angolare vi sono due stati quantici con lo spin intrinseco dei nucleoni rivolto in direzioni opposte). L'esistenza di gusci maggiori è più evidente nel potenziale dell'oscillatore armonico in cui vi sono varie combinazioni di n ed l con esattamente le stesse energie E(n,l). Invece i gusci maggiori sono in numero minore nel potenziale di Woods-Saxon in cui gli stati con l grande sono legati più strettamente che nel potenziale dell'oscillatore armonico, perché la grande forza centrifuga obbliga le particelle di questi stati con l grande a rimanere nelle regioni esterne del nucleo, dove il potenziale di Woods-Saxon presenta un'attrazione più forte di quello dell'oscillatore armonico. Altri potenziali V(r) producono altri schemi di energie E(n,l) e altri raggruppamenti di guscio maggiore.

L'esistenza di raggruppamenti di guscio maggiore dà origine a delle irregolarità nell'energia di legame nucleare B(N,Z) per alcuni numeri magici' di neutroni e di protoni. Il numero magico N₀ o Z₀ di un guscio maggiore è il numero totale di neutroni o di protoni che possono essere sistemati in stati quantici all'interno di quel guscio maggiore o in gusci più strettamente legati. L'energia di legame B(N,Z) cresce meno rapidamente al crescere di N quando N è di poco superiore a un numero magico N₀ di quanto non cresca quando N è di poco inferiore a N₀, perché, per il principio di Pauli, i neutroni aggiunti devono occupare degli stati quantici, (n,l) meno favorevoli. La stessa cosa vale per i protoni quando Z è nelle vicinanze di Z₀. I numeri magici per i protoni non sono necessariamente gli stessi di quelli per i neutroni, perché il potenziale V(r) dei protoni è diverso, specialmente nei nuclei pesanti. Per i potenziali dell'oscillatore armonico e di Woods-Saxon delle figg. 12 e 13 i numeri magici sono rispettivamente 2, 8, 20, 40, 70, 112 e 2, 8, 20, 40, 92. I numeri magici ricavati dalle misure dell'energia di legame B(N,Z) e da altri dati noti sono uguali per i neutroni e per i protoni: 2, 8, 20, 28, 50, 82 e, per i neutroni, 126. Mentre molti potenziali hanno gusci maggiori con 2, 8 e 20 nucleoni, i numeri magici 28, 50, 82 e 126 non possono invece essere spiegati con nessuna forma ragionevole di V(r).

Le forze dipendenti dallo spin tra coppie di nucleoni danno origine a un potenziale medio su un nucleone all'interno di un nucleo che non dipende soltanto dalla sua posizione r, ma anche dall'angolo tra le direzioni dello spin S e del momento della quantità di moto ℒ. Questa dipendenza può essere espressa approssimativamente mediante un poterziale addizionale V^ls(r) ℒ•S, detto potenziale di spin-orbita. A causa di questo potenziale, l'energia E dello stato quantico di un nucleone dipende non soltanto da n e da l, ma anche dal momento angolare totale che può avere i valori ℱ = √-j-(-j-+-1-) ℏ, dove j = l + ½ o l − ½ a seconda della direzione di S rispetto a ℒ. I 2(2j + 1) stati quantici di ogni sottoguscio non hanno più la stessa energia, ma sono divisi in due sottogusci di 2j + 1 stati quantici ciascuno, per i due valori di j. I nucleoni con j = l + ½, cioè con spin parallelo a ℒ, sono legati insieme più strettamente di quelli con spin antiparallelo. La fig. 14 dà un esempio di potenziale di questo tipo, i cui gusci maggiori riproducono i numeri magici osservati. L'idea che la forte dipendenza del potenziale nucleare dalla direzione dello spin del nucleone potesse spiegare i numeri magici non fu acquisita facilmente: infatti l'esistenza dei numeri magici era già nota da ben quindici anni prima che il brillante lavoro di Mayer e di Jensen, Haxel e Suess ne desse la spiegazione.

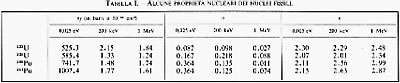
L'esistenza dei numeri magici e i loro valori, insieme a molte altre misure relative alle proprietà nucleari (alcune delle quali saranno trattate più avanti), hanno fornito delle buone prove dell'esistenza dei potenziali nucleari medi V(r) e V^ls(r) e hanno dato anche un certo numero di informazioni riguardo alle loro caratteristiche. I potenziali sono stati calcolati anche sulla base della teoria nucleare a molti corpi, a partire dalle forze determinate per mezzo degli esperimenti di diffusione di due nucleoni. Un calcolo di questo tipo si chiama calcolo a campo autocompatibile, perché la forza che agisce su ogni particella dev'essere quella media prodotta da tutte le altre, mentre il suo moto serve a determinare le forze che agiscono sulle altre particelle. In questo modo sono state calcolate le distribuzioni di densità e le energie di legame di vari nuclei. I risultati sono sensibili alle caratteristiche della forza interagente tra due nucleoni, ma è stato possibile riprodurre le distribuzioni dei nucleoni e le energie di legame osservate partendo da una forza simile a quella descritta nel cap. 3 (v. fig. 11), la quale riproduce anche le proprietà osservate della diffusione neutrone-protone e protone-protone. Alcuni risultati di tale calcolo sono riportati nella fig. 15 e nella tab. I. È possibile misurare le energie E(n,l) relative al moto di ogni singola particella nel campo medio mediante esperimenti in cui un nucleone viene aggiunto o sottratto a un nucleo ‛magico'. Anche in questo caso si è potuta ottenere una buona corrispondenza tra le energie E(n,l) misurate sperimentalmente e quelle calcolate mediante la teoria a molti corpi a campo autocompatibile. Tanto l'energia E(n,l) misurata quanto quella calcolata col campo autocompatibile mostrano che il potenziale medio V(r) a cui è soggetto un nucleone all'interno del nucleo dipende dai valori n,l e anche da E(n,l). Nella tab. Il è riportato un esempio delle energie calcolate e di quelle misurate necessarie per rimuovere un nucleone da stati quantici differenti in un nucleo di calcio.

Con dei lievi perfezionamenti il ‛modello a guscio' di singoli nucleoni che si muovono indipendentemente nel campo medio generato dagli altri nucleoni può essere esteso a spiegare molti altri fenomeni nucleari, oltre ai numeri magici. Come si è detto nei capp. 3 e 4, l'intensa forza tra ciascuna coppia di nucleoni all'interno di un nucleo ha generalmente solo un piccolo effetto sul moto dei due nucleoni che interagiscono, perché, dopo la collisione, essi devono ritornare ai loro stati quantici originali, essendo gli altri stati quantici di uguale energia occupati da altri nucleoni. Le eccezioni a questa regola si hanno per quelle particelle che occupino degli stati quantici in sottogusci aventi all'incirca la stessa energia e i cui stati quantici non siano tutti occupati: in questo caso i nuclei che sono entrati in collisione possono rimanere in uno di questi altri stati quantici vuoti di energia quasi eguale. Di conseguenza i moti dei nucleoni che occupino stati quantici di energia vicina sono legati gli uni agli altri in maniera molto più stretta che non sotto l'effetto del solo campo nucleare medio. In tal caso il loro moto si dice ‛correlato'. Una correlazione nel moto dei nucleoni i cui stati quantici nel modello a guscio appartengano a sottogusci di energia vicina si chiama ‛correlazione di quadrupolo': in questo caso i nucleoni vengono a trovarsi dalla stessa parte del nucleo allo stesso istante di tempo. A un'altra correlazione importante viene dato il nome di ‛appaiamento' perché il moto che ne risulta è tale per cui i nucleoni sono raggruppati in coppie di due nucleoni che ruotano in direzioni opposte. Questo moto appaiato permette a ogni coppia di nucleoni di trarre maggior vantaggio dalla forza di attrazione reciproca che non nel caso in cui si muovano indipendentemente l'uno dall'altro. In un nucleo con un numero dispari di neutroni o di protoni uno dei nucleoni rimane senza compagno e quindi l'energia di legame totale è minore di quella che si avrebbe se tutti i nucleoni fossero riuniti in coppie. Questa è l'origine dell'energia di appaiamento' B^P riscontrata nella formula di massa semiempirica dell'equazione (2). Inoltre il momento della quantità di moto totale di un nucleo nel suo stato fondamentale è eguale al solo momento del nucleone ‛spaiato', poiché il momento angolare totale di una coppia di nucleoni che ruotano in direzioni opposte è nullo. Gli stati fondamentali di tutti i nuclei con N e Z pari hanno momento uguale a zero. In questo modo il modello a guscio dà ragione del momento misurato di ogni stato fondamentale del nucleo. Se si prendono poi in considerazione gli effetti delle correlazioni, si possono spiegare anche i momenti magnetici misurati degli stati nucleari fondamentali.

La maggior parte dei nuclei puo esistere in stati eccitati in cui un nucleone, o più d'uno, non sta nello stato quantico (n,l,j) più strettamente legato che ha a disposizione, ma in uno meno strettamente legato. Sono stati osservati molti stati eccitati di questo tipo in cui le energie di legame e i momenti delle quantità di moto possono essere spiegati col modello a guscio. Normalmente un nucleo rimane in uno di questi stati eccitati per un tempo breve, dell'ordine di 10^-16 secondi, prima di trasformarsi in una struttura più strettamente legata, per emissione di un quanto di luce. Tuttavia, se il momento angolare dello stato eccitato differisce molto da quello degli stati legati più strettamente, il nucleo può rimanere nello stato eccitato per delle ore, o anche più a lungo, perché i fotoni a bassa energia non hanno tendenza a portare via grandi momenti angolari. Questi stati eccitati di lunga durata sono chiamati ‛isomeri'.

In un nucleo in cui vi siano più neutroni che protoni, alcuni neutroni devono trovarsi in stati quantici (n, l, j) del modello a guscio, il cui stato quantico protonico corrispondente non è occupato. In un tale stato quantico un neutrone può essere sostituito da un protone che si muova quasi nello stesso modo, perché le forze nucleari sono praticamente indipendenti dalla carica elettrica dei nucleoni. Lo stato nucleare risultante del nucleo (N − I, Z + 1) ha quindi circa la stessa energia di legame dello stato originale del nucleo (N,Z) fuorché per l'energia potenziale elettrica del nuovo protone. Se il nucleo originale aveva un numero di neutroni maggiore soltanto di un'unità del numero dei protoni, i due nuclei si dicono ‛nuclei speculari' e le energie di legame sia dei loro stati fondamentali sia dei loro stati eccitati differiscono solo per il potenziale elettrico di un protone. Se nel nucleo originale c'erano invece assai più neutroni che protoni, allora lo stato fondamentale e quelli eccitati hanno delle corrispondenze negli stati eccitati di vari altri nuclei in cui uno, due o più neutroni sono sostituiti da protoni. Tali coppie o gruppi di stati sono detti ‛analoghi isobarici'. In questo modo, poiché le forze nucleari sono quasi indipendenti dalla carica, ogni stato nucleare può essere caratterizzato dall'eccesso di neutroni T = (N - Z)/2 del nucleo più ricco di neutroni in cui ha un analogo isobarico. La differenza di energia di legame tra due stati analoghi isobarici, qual è dovuta principalmente al potenziale elettrico addizionale del protone, può essere sfruttata per calcolare le distanze medie del protone dal centro del nucleo. Nei pochi casi in cui questa distanza può essere misurata anche in modo indipendente (per es., mediante la diffusione di elettroni), si trova che la differenza nell'energia di legame degli stati analoghi isobarici è molto simile a quella dovuta al potenziale elettrico; la discordanza rimanente si può spiegare con una differenza di circa il 3% sussistente nelle forze di attrazione tra due neutroni e due protoni.

5. Stati collettivi.

Una delle caratteristiche più singolari dei nuclei è il fatto che non sono rotondi. Come è stato detto nel cap. 2, le misure dei campi elettrici prodotti dai nuclei dimostrano che molti di essi sono di forma ovoidale. Un bombardamento eseguito con un qualsiasi tipo di proiettile imprime a un nucleo deformato un moto di rotolamento intorno a un asse che passa attraverso il suo centro di massa. Per avviare una rotazione di questo genere è sufficiente una frazione di MeV, cioè un'energia molto minore di quella necessaria per eccitare un nucleone a uno stato quantico in un sottoguscio diverso. Quindi non si debbono interpretare le forme nucleari, e le eccitazioni nucleari a esse associate, mediante il moto indipendentemente quantizzato dei singoli nucleoni che sta alla base del modello a guscio.

Nel 1950 Rainwater fece notare che il potenziale medio V(r) in un nucleo non sferico non dovrebbe essere sferico, ma dovrebbe avere la stessa forma della densità dei nucleoni che lo producono. In seguito Bohr e Mottelson mostrarono come le deformazioni nucleari siano il risultato della forza di attrazione tra i nucleoni.

I nucleoni che occupino stati quantici in un guscio incompleto possono trarre il maggior vantaggio dalle forze di attrazione esistenti tra di loro, ponendosi negli stati quantici in cui il moto li tiene saldamente insieme. Di solito questo avviene nel modo migliore quando il moto dei nucleoni si concentra lungo un asse, cosicché la densità di nucleoni, nelle regioni esterne del nucleo, è massima vicino ai poli e minima vicino all' equatore. La forza di attrazione media cui è soggetto il nucleone diventa quindi più intensa vicino ai poli che vicino all'equatore, perché gli altri nucleoni sono vicini ai poli: di conseguenza gli stati quantici in cui il nucleone passa la maggior parte del tempo vicino ai poli hanno le energie di attrazione maggiori. I nucleoni in un guscio incompleto scelgono evidentemente gli stati quantici più strettamente legati: quindi vengono a concentrarsi vicino ai poli dove contribuiscono a creare il potenziale attrattivo medio che porta lì gli altri nucleoni.

Nella fig. 16 è riportato un esempio del calcolo degli stati quantici relativi al moto in un potenziale non sferico. In ordinata sono riportate le energie dei vari stati quantici per un potenziale la cui deformazione è data in ascissa. Il parametro δ misura la differenza tra la lunghezza e il diametro del nucleo, secondo quanto è mostrato nella fig. 17. Quando è δ = 0, i livelli si presentano in gruppi di (2j + 1) corrispondenti alle diverse orientazioni possibili del moto del nucleone per un egual valore del momento della quantità di moto. Quando è δ 〈 0, è favorito il moto lungo l'asse del nucleo, come dimostra la diminuzione dell'energia, mentre è sfavorito il moto equatoriale, indicato dalle linee di energia crescenti. Ogni linea rappresenta ora due soli stati quantici in cui i nucleoni circolano in direzioni opposte ma a distanza uguale dai poli. In questa figura, nello stato fondamentale di un nucleo con N neutroni e deformazione δ i neutroni si trovano negli N stati quantici più strettamente legati. Se N è pari, il momento risultante della quantità di moto del nucleo sarà eguale a zero, perché i momenti di ciascuna coppia di nucleoni aventi la stessa energia si elidono completamente a vicenda. La forma effettiva dello stato fondamentale di un nucleo è quella che rende minima la sua energia totale.

In questo modo, il moto di molti nucleoni può essere correlato in maniera tale che essi tendano a stare vicino allo stesso asse. Questo asse non è orientato in alcuna direzione particolare dello spazio, perché non c'è alcuna ragione per cui i nucleoni scelgano di allinearsi in una direzione piuttosto che in un'altra: quello che è importante è che ogni nucleone si allinei con gli altri, ovunque essi siano. Invero, l'asse nucleare può persino ruotare lentamente. Le rotazioni lente dell'intera struttura oblunga del nucleo si debbono considerare come stati nucleari eccitati con bassa energia di eccitazione. Il moto rotazionale implica un certo momento della quantità di moto che può assumere i valori quantizzati ℱ = √-J-(-J-+-1-) ℏ, con J = 0, 1, 2 ecc. La quantizzazione del momento della quantità di moto porta a una serie di stati eccitati con energia

E_x = J(J +1)ℏ²/2ℑ, (8)

dove ℑ rappresenta il momento di inerzia del nucleo. Una serie di livelli di questo genere è caratteristica degli spettri dei nuclei deformati. Il momento di inerzia ℑ dà un'indicazione della massa del nucleo che prende parte alla rotazione: un valore grande di ℑ indica che il moto coinvolge molti nucleoni. Nei casi tipici si trova che ℑ è molto grande, di grandezza compresa tra un mezzo e un quinto del valore che si avrebbe se l'intero nucleo ruotasse come un corpo rigido. Un valore così grande di ℑ dà luogo a stati quantici eccitati con bassa energia di eccitazione E_x, secondo quanto è espresso dall'equazione (8).

Il moto simultaneamente correlato di molti nucleoni che porta a una forma allungata del nucleo rappresenta un tipo di correlazione di natura molto diversa dalla correlazione di appaiamento di cui si è trattato nel cap. 4 in connessione con il modello a guscio. Il problema del rapporto tra questi due tipi di correlazione dà luogo a uno dei più entusiasmanti capitoli della fisica nucleare, in cui si vanno ancora scoprendo nuovi fenomeni. La correlazione di appaiamento è più vantaggiosa nei nuclei sferici, in cui le particelle possono scegliere tra molti stati quantici della stessa energia con orientazioni diverse dei momenti delle quantità di moto. In un nucleo deformato, gli stati quantici dei nucleoni con diverse orientazioni hanno energie differenti (come è illustrato nella fig. 16). L'appaiamento richiederebbe quindi un cambiamento dello stato quantico dei nucleoni della coppia verso stati a energia più alta, di modo che si perderebbe gran parte del vantaggio dell'appaiamento. Il moto dei nucleoni nei nuclei reali è un compromesso tra questi due tipi di correlazione. Nei nuclei con pochi nucleoni in più del numero magico le correlazioni di appaiamento sono più vantaggiose della deformazione. A mano a mano che vengono aggiunti dei nucleoni, la deformazione diventa sempre più vantaggiosa perché aumenta il numero dei nucleoni che condividono l'attrazione, gli uni degli altri, vicino ai poli nucleari. Quando c'è un numero sufficiente di nucleoni nel guscio incompleto, la correlazione dovuta alla forma elongata diventa più vantaggiosa della correlazione di appaiamento. Quindi, accrescendo il numero dei nucleoni oltre un nucleo magico, si ha un'improvvisa transizione dai nuclei sferici - con correlazione di appaiamento e con sole tracce di correlazioni non sferiche - a nuclei elongati con una correlazione a coppie assai meno evidente. Anche nei nuclei elongati c'è però ancora una considerevole correlazione a coppie; ciò è alla base del motivo per cui la rotazione di un nucleo deformato non coinvolge tutti i nucleoni. Se non ci fossero correlazioni di appaiamento, un nucleo deformato potrebbe ruotare attorno al proprio asse come un corpo rigido con un momento d'inerzia molto più grande di quello realmente osservato. La fig. 18 mostra alcuni momenti di inerzia, misurati, confrontati con quelli ottenuti dalla rotazione del nucleo nel suo insieme, e quelli calcolati tenendo conto della correlazione di appaiamento. Questi momenti d'inerzia sono misurati e calcolati per stati eccitati in cui il nucleo ruota molto lentamente. Recenti scoperte indicano che alcuni nuclei hanno un momento d'inerzia molto maggiore quando ruotano rapidamente che quando ruotano lentamente; si pensa che questo stia a indicare che la correlazione di appaiamento sia ulteriormente indebolita in un nucleo in rapida rotazione.

I nuclei con un numero di neutroni e di protoni prossimo a un numero magico assumono generalmente forma sferica a causa dei gusci degli stati quantici che hanno energia quasi uguale, caratteristici dei nuclei sferici. Nel 1966 Strutinski fece notare come tali gusci possano esistere anche in nuclei molto elongati. Per esempio, se il diametro maggiore di un nucleo è doppio del diametro minore, impiegando la stessa quantità di energia si può produrre un'onda con due nodi nel senso della lunghezza oppure un'onda con un solo nodo nel senso della larghezza del nucleo. Vi sono dunque numeri magici per nuclei lunghi due volte la loro larghezza, i quali possono avere stati eccitati relativamente stabili, chiamati ‛isomeri di forma', che sono molto elongati. Tali stati eccitati sono stati di recente osservati nella fissione di nuclei pesanti.

La rotazione di un nucleo non sferico è soltanto un esempio della collaborazione possibile tra un gran numero di nucleoni in un moto di tipo ‛collettivo', che richiede pochissima energia per essere eccitato. Gli spettri degli stati eccitati dei nuclei sferici sono anche indicativi della capacità che hanno i nucleoni di seguire gli uni il moto degli altri. Non occorre molta energia perché un nucleo sferico assuma una forma oblunga o appiattita: infatti basta una lieve spinta da parte di un protone, di una particella alfa o di un raggio gamma per imprimere a un nucleo sferico un moto vibratorio, per il quale esso oscilla da una forma piatta a una oblunga intorno a quella sferica di equilibrio. Un'oscillazione di questo tipo si chiama ‛oscillazione di quadrupolo', perché la deformazione della forma del nucleo produce una componente alternata del campo elettrico con caratteristiche angolari che nella teoria elettromagnetica prendono il nome di ‛quadrupolo'. Questo campo elettrico alternato dà luogo a radiazione dell'energia di vibrazione sotto forma di un quanto elettromagnetico. L'intensità della radiazione che ne risulta dà una misura dell'ampiezza della vibrazione nucleare, così come il campo elettrostatico intorno a un nucleo non sferico misura la deformazione di quest'ultimo. Sono state osservate anche delle vibrazioni nucleari che comportano deformazioni d'altra forma, la più importante delle quali è quella di ‛ottupolo' in cui si ha una deformazione a forma di pera, illustrata nella fig. 19.

Il campo elettromagnetico del nucleo rende anche possibile distinguere moti nucleari collettivi che richiedono maggiori energie per l'eccitazione. La risposta di un nucleo alla radiazione gamma elettromagnetica di energia moderata (fino a 50 MeV) è dominata dai moti collettivi, perché la lunghezza d'onda della radiazione è così lunga che l'onda è prodotta coerentemente da tutte le particelle in movimento. La potenza assorbita o irradiata è proporzionale al quadrato della quantità di carica in movimento, di modo che il moto collettivo, quello cioè in cui molti protoni si muovono simultaneamente, è accoppiato in maniera particolarmente forte al campo della radiazione elettromagnetica. Questa caratteristica spiega il fatto che i fotoni con energia di circa 20 MeV sono assorbiti molto fortemente da tutti i nuclei. Questi fotoni possono produrre un moto di tipo vibratorio in cui protoni e neutroni si muovono in verso opposto. L'energia necessaria per un moto del genere è grande perché i protoni e i neutroni si attraggono molto fortemente; ciononostante il carattere sincrono del moto di tutti i protoni del nucleo lo rende facilmente eccitabile da parte di raggi gamma di sufficiente energia.

Sono possibili molte eccitazioni nucleari oltre al semplice moto delle particelle singole e alle rotazioni e vibrazioni collettive. I due tipi di moto si possono combinare in vari modi: per esempio, un nucleone in un nucleo rotante può essere considerato come soggetto alla forza non inerziale di Coriolis dovuta alla rotazione del nucleo, che è il suo sistema di riferimento. Gli effetti di questa forza di Coriolis possono per esempio essere visti come un momento di inerzia variabile in funzione della velocità di rotazione nucleare. Gli stati nucleari in cui una o più particelle vengono eccitate dagli stati quantici più bassi del modello a guscio possono anche essere deformati e posti in rotazione.

In un nucleo in vibrazione anche i singoli nucleoni debbono risentire dell'effetto del cambiamento col tempo del loro potenziale medio e questo effetto diviene particolarmente evidente in un nucleo che abbia una particella in più del nucleo magico. Quando un nucleo del genere è posto in vibrazione, l'energia della vibrazione dipende dall'orientazione relativa dell'asse lungo il quale il nucleo si allunga o si accorcia durante la vibrazione e dal momento angolare del nucleone addizionale. Effetti di questo tipo sono oggi studiati intensamente.

6. Collisioni nucleari.

Sin dalla prima osservazione di Rutherford delle collisioni tra nuclei di elio e di oro, gli immensi sforzi compiuti per lo studio delle reazioni nucleari sono stati ricompensati da considerevoli progressi nella comprensione non soltanto dei meccanismi secondo cui esse avvengono, ma anche della struttura degli stati nucleari che si producono nel corso delle reazioni. Nell'esperimento originale di Rutherford, i nuclei di oro e di elio rimanevano sempre nello stato fondamentale e quelli di elio rimbalzavano semplicemente su quelli di oro senza cambiare il loro moto interno. Queste collisioni si dicono di tipo elastico. Spesso la collisione tra due nuclei provoca in uno di questi, o in tutti e due, l'eccitazione di qualche moto interno: rotazione, vibrazione, cambiamento del moto di uno dei nucleoni, ecc. Una collisione di questo tipo viene detta anelastica, perché parte dell'energia del moto che le particelle avevano prima della collisione serve a cambiare gli stati interni dei nuclei. Può anche accadere che uno o più nucleoni di un nucleo rimangano nell'altro dopo lo scontro, formando così una diversa specie nucleare, o che invece uno dei nuclei espella una o più delle particelle che lo costituiscono; a questo genere di collisione si dà il nome di processo di ‛riordinamento' o di ‛trasferimento'.

Il risultato di una collisione nucleare può essere osservato in vari modi, che possono essere approssimativamente divisi in due gruppi. Nel primo tipo di esperimenti si osservano i prodotti della collisione quando lasciano il bersaglio e se ne misura la carica, la massa, la velocità, la direzione del moto, ecc. La massa, l'energia e la carica di una particella possono essere facilmente determinate misurando, spesso con un rivelatore a semiconduttore costruito appositamente a tal fine, la ionizzazione prodotta. Una misura più precisa dell'energia della particella si può ottenere dall'analisi della traiettoria che essa segue in un campo magnetico.

I metodi del secondo tipo, per l'osservazione del risultato delle collisioni nucleari, si basano sullo studio dei prodotti della reazione quando non sono più in movimento. La composizione del bersaglio può essere determinata chimicamente oppure mediante l'osservazione della radioattività gamma e beta. Se il nucleo in esame non rimane nel bersaglio, si può analizzare il mezzo intorno a questo o il gas nella camera bersaglio. Questo secondo metodo è particolarmente indicato per le reazioni in cui si producono soltanto particelle lente o in cui si devono determinare simultaneamente i prodotti di molte reazioni diverse, mentre il primo metodo in genere è in grado di fornire informazioni molto più dettagliate sulla reazione. In particolare dall'energia cinetica del prodotto di una reazione si può determinare l'energia dello stato nucleare eccitato che si è prodotto, mentre la quantità relativa di particelle osservate ad angoli diversi rispetto al fascio incidente offre spesso delle indicazioni sulle proprietà dello stato nucleare prodotto, oltre che sul meccanismo della reazione.

A causa delle forze elettriche tra protoni, tutti i nuclei si respingono reciprocamente, a meno che non siano così vicini che le loro distribuzioni di materia si sovrappongano in parte ed entrino quindi in gioco le forze attrattive nucleari a corto raggio. Per produrre, quindi, reazioni nucleari in grande quantità è necessario accelerare i nuclei fino a che la loro energia cinetica non sia grande quanto l'energia potenziale elettrica dei due nuclei all'istante in cui si toccano, di modo che essi possano superare la barriera costituita dal potenziale elettrico repulsivo. Poiché questa barriera di potenziale è proporzionale alla carica elettrica del proiettile e poiché è tecnicamente difficile accelerare nuclei pesanti, la maggior parte delle reazioni nucleari sinora studiate sono iniziate da proiettili leggeri, cioè neutroni, protoni, deutoni o nuclei di elio. Nell'ultimo decennio sono stati costruiti degli acceleratori che sono in grado di accelerare nuclei pesanti sino a energie sufficienti per innescare reazioni nucleari con nuclei bersaglio pesanti e presto sarà possibile osservare perfino le reazioni che avvengono quando si scontrano anche i nuclei più pesanti.

Affinché si possa verificare un'interazione fra due nuclei, essi devono possedere, secondo la fisica classica, energia cinetica relativa sufficiente per superare la barriera di energia potenziale esistente tra loro. Secondo la meccanica quantistica, invece, un nucleo può penetrare per ‛effetto tunnel' attraverso una barriera di potenziale, anche quando non abbia l'energia cinetica sufficiente per raggiungere il suo traguardo secondo la teoria classica del moto. La funzione d'onda che descrive il moto relativo dei due nuclei non si ferma improvvisamente nel punto in cui deve fermarsi la particella classica, ma esiste invece una piccola ‛coda' di probabilità, rapidamente decrescente, che i nuclei si trovino nella paradossale situazione di avere più energia potenziale che totale (v. fig. 20). La probabilità che i nuclei riescano a penetrare per effetto tunnel attraverso la regione proibita cresce rapidamente al crescere della loro energia. L'esempio più significativo di questo fenomeno è dato dal decadimento radioattivo di un nuclide pesante in un nucleo di elio (cioè una particella alfa) e un nucleo residuo con due protoni e due neutroni in meno. Questa reazione nucleare produce un nucleo di elio con un'energia cinetica compresa tra circa 4 e 8 MeV, mentre l'energia elettrica potenziale di un nucleo di elio vicino a un nucleo pesante, come il radio, è certamente superiore a 20 MeV. Il fatto che il nucleo di elio riesca a sfuggire dal nucleo pesante significa che la sua funzione d'onda è penetrata attraverso una regione in cui, secondo la fisica classica, non si potrebbe mai trovare il nucleo di elio. Naturalmente questa deviazione dalle regole della fisica classica è molto piccola: nei casi tipici, per ogni nucleo di elio che penetra nella regione proibita, ve ne sono tra 10¹⁰ e 10³⁰ che sono respinti e riassorbiti dal nucleo pesante. Nelle reazioni nucleari prodotte per collisione, gli effetti della penetrazione nella barriera non sono di solito sufficientemente grandi da essere rivelabili, a meno che la particella che penetra nella barriera non abbia un'energia cinetica che si discosta di non più di qualche MeV dal potenziale massimo. Nel caso della radioattività alfa, la particella alfa continua a urtare contro l'interno della barriera di potenziale fino a che riesce a superarla, ma, perché questo accada, può essere necessario moltissimo tempo: per esempio, un nucleo di ²³²Th in 10¹⁰ anni ha soltanto una probabilità del 50% di emettere una particella alfa e un nucleo di ¹⁴⁷Sm ha eguale probabilità in un tempo medio di 10¹¹ anni. In realtà la maggior parte dei nuclei con A 〈 100 potrebbe emettere una particella alfa, ma con un'energia così bassa che il processo avverrebbe tanto di rado da non poter essere osservato.

Quando due nuclei si sono sufficientemente avvicinati l'uno all'altro, le intense forze a corto raggio che sorgono dallo scambio di mesoni fanno sì che i nucleoni di un nucleo influenzino quelli dell'altro. Queste interazioni sono molto complicate a causa delle numerose configurazioni che i nucleoni potrebbero assumere, e che assumono realmente, durante l'interazione. Fortunatamente in molti casi queste interazioni possono essere rappresentate abbastanza bene mediante un'energia potenziale media che dipende dalla posizione e, in misura minore, dalla velocità dei nuclei che si urtano. Il moto relativo dei nuclei è rappresentato da una funzione di probabilità che soddisfa l'equazione di Schrödinger in questo potenziale medio. Ma il moto relativo dei due nuclei non è l'unica cosa che avviene durante la collisione; possono anche prodursi delle reazioni in cui i nuclei cambiano caratteristiche, ponendosi in stati eccitati o scambiandosi nucleoni. Il fatto che avvengano reazioni di questo genere indica che diminuisce la probabilità di trovare i due nuclei originali; nel corso dell'interazione, quindi, deve corrispondentemente diminuire l'ampiezza della funzione di probabilità. Ciò può essere rappresentato mediante un potenziale immaginario nell'equazione di Schrödinger per la loro funzione d'onda. L'energia rappresenta, nell'equazione di Schrödinger, la frequenza dell'onda di de Broglie; un valore immaginario dell'energia rappresenta quindi un decadimento esponenziale temporale della funzione d'onda. Una scelta opportuna del potenziale immaginario può riprodurre la diminuzione della probabilità di trovare i due nuclei nei loro stati fondamentali originari.

Il concetto di potenziale medio di questo tipo, chiamato ‛potenziale ottico', è stato impiegato con grande successo per spiegare molte caratteristiche medie delle collisioni tra proiettili, contenenti fino a sei nucleoni, e nuclei bersaglio, grandi e piccoli. L'utilità di questo concetto negli urti tra due nuclei complessi deve essere ancora dimostrata, forse per l'incompletezza delle misure sperimentali attualmente disponibili.

L'esempio più studiato del concetto di potenziale ottico è dato dalla diffusione elastica di neutroni su nuclei. La capacità di un nucleo di deviare neutroni di energia E viene espressa per mezzo della sua cosiddetta ‛sezione d'urto' σ(E). Le sezioni d'urto osservate per un fascio contenente neutroni di energia compresa in un intervallo di circa 0,1 MeV intorno all'energia media E mostrano una dipendenza assai regolare dal numero atomico A del bersaglio e dall'energia E del fascio di neutroni. Nella fig. 21 sono riportate le sezioni d'urto totali di molti nuclei per diffusione di neutroni di varia energia. L'energia corrispondente alle sezioni più grandi varia in maniera regolare con la dimensione del nucleo bersaglio; ciò può essere spiegato in base alla crescita del raggio della regione in cui il neutrone risente dell'attrazione dei nuclei più grandi e anche in base alla diminuzione dell'intensità dell'attrazione dovuta all'eccesso di neutroni dei nuclei più pesanti. Il potenziale ottico dei protoni è simile a quello dei neutroni, se si eccettua il fatto che l'attrazione nucleare è maggiore per i nuclei più grandi che hanno meno protoni che neutroni; differenza, questa, più che controbilanciata dal contributo repulsivo delle forze elettrostatiche al potenziale ottico.

Un'analisi accurata della diffusione elastica dei neutroni da parte dei nuclei ha portato alla conclusione che l'attrazione di cui risente un neutrone veloce è minore di quella di cui risente un neutrone lento. Questo risultato in verità non sorprende, se si ricorda il fatto che la forza che agisce su un neutrone è l'effetto medio di molte collisioni con nucleoni singoli, in ognuna delle quali la forza dipende dalla velocità relativa delle particelle che si urtano. Sono stati fatti dei calcoli in cui il potenziale ottico per neutroni e per protoni è stato dedotto dalla teoria nucleare a molti corpi, in analogia a quanto è stato fatto per il potenziale medio del modello a guscio. Questo calcolo è complicato dalla necessità di tener conto dell'effetto del nucleone ‛estraneo' sul moto degli altri nucleoni.

Nel caso della diffusione di neutroni con energia cinetica inferiore a circa 1 MeV è stato possibile studiare molto dettagliatamente le sezioni d'urto delle reazioni. Per quanto il comportamento medio delle sezioni d'urto possa essere compreso per mezzo del potenziale ottico, queste sezioni mostrano delle variazioni rapide con l'energia, nella forma di massimi stretti di larghezza compresa tra 0,1 e 10⁴ elettronvolt. Per bassi valori dell'energia questi massimi si susseguono a intervalli irregolari pari a varie volte la loro larghezza (v. fig. 22), mentre agli alti valori cresce la larghezza media dei massimi e decresce invece l'intervallo medio tra di essi, fino a che alla fine i massimi si fondono insieme. Per valori dell'energia E vicini a un valore E₀, al quale la sezione σ(E) raggiunge un valore massimo σ_m, la sezione d'urto può essere rappresentata dalla formula di Breit-Wigner

dove F rappresenta la larghezza del massimo. Un massimo di questo tipo nella sezione d'urto viene chiamato ‛risonanza' e corrisponde a uno stato del sistema neutrone-nucleo nel quale il neutrone, sebbene non sia proprio legato al nucleo, divide per un certo tempo la sua energia con tanti nucleoni che non si può allontanare subito dal nucleo, ma vi rimane dentro per un tempo T abbastanza lungo. Per il principio di indeterminazione di Heisenberg, la relazione tra il tempo T durante il quale il sistema rimane nello stato di risonanza e l'intervallo di energia in cui lo stato risonante appare è la seguente:

ΓT = ℏ. (10)

Quindi Γ è proporzionale alla velocità con cui il sistema risonante costituito dal neutrone e dal nucleo decade in altri stati. Questo decadimento può avvenire in vari modi e la velocità totale è uguale alla somma delle velocità delle varie reazioni che possono avvenire nel sistema neutrone-nucleo, secondo l'equazione

in cui ogni Γ_i, detto ‛larghezza parziale', è proporzionale alla velocità con cui avviene l'i-esimo processo nel sistema neutrone-nucleo. I processi più importanti sono la radiazione di un quanto di luce, cui è associata una ‛larghezza di radiazione' Γ_x, e la fuga di un neutrone dal nucleo, cui è associata una ‛larghezza neutronica' Γ_n. La larghezza neutronica può essere considerata come il prodotto di due fattori: la probabilità che un neutrone di particolare energia riesca a uscire dal nucleo, cui si dà il nome di ‛fattore di penetrazione', e la probabilità, detta ‛larghezza ridotta', che uno dei neutroni del nucleo abbia quella determinata energia.

La previsione delle energie e delle larghezze di tutte le numerose risonanze osservate è un compito senza speranza, dal momento che esse rappresentano stati assai complessi in cui l'energia di eccitazione si suddivide in modo complicato tra molti nucleoni. Invece di tentare di comprendere con precisione ogni singolo stato, si è costruita una teoria statistica per mettere in relazione il numero medio di livelli per keV, la loro larghezza media e l'intensità media con cui essi vengono eccitati con le proprietà nucleari medie, come il numero di particelle del nucleo e i potenziali ottici dei neutroni e dei protoni. Questa teoria statistica è stata utilizzata per dar ragione non soltanto dei valori medi di queste grandezze, ma anche delle loro distribuzioni intorno ai valori medi. Anche nelle reazioni tra protone e nucleo si sono trovate delle risonanze, ma molto più deboli, perché la barriera repulsiva del potenziale elettrico che circonda il nucleo ha l'effetto d'isolare il moto del protone all'esterno del nucleo dal moto all'interno.

I sottili picchi di risonanza osservati nella diffusione dei neutroni da parte di un nucleo a bassa energia costituiscono un'ottima conferma di un modello di reazioni nucleari proposto per la prima volta da Niels Bohr nel 1935, secondo cui si ipotizzava la formazione di un sistema composto, in cui proiettile e bersaglio si mescolano insieme perdendo la loro identità, seguita, molto più tardi, dalla disintegrazione del sistema composto nei prodotti della reazione. Il fatto che proiettile e bersaglio perdano la loro identità significa che, se nel corso di reazioni diverse si forma lo stesso sistema composto caratterizzato dallo stesso numero totale di neutroni e di protoni, dallo stesso momento angolare e dalla stessa energia, le probabilità relative di formazione dei vari prodotti della reazione saranno indipendenti dal modo in cui si è formato il sistema composto e la distribuzione angolare della direzione del moto dei prodotti della reazione dipenderà in maniera regolare dall'angolo formato con la direzione dei proiettili incidenti. L'energia con cui il proiettile è entrato nel nucleo bersaglio sommata all'energia dovuta all'interazione tra i nucleoni del proiettile e quelli del bersaglio viene ridistribuita tra tutti i gradi di libertà del sistema combinato. Si può allora parlare di temperatura del nucleo composto, qual è data dall'energia di eccitazione media di ogni grado di libertà. Si può, inoltre, far uso del formalismo della meccanica statistica per predire la probabilità che un singolo nucleone, o un aggregato più complicato come una particella alfa, abbia energia sufficiente per sfuggire dal nucleo; questa quantità, moltiplicata per la probabilità che un nucleone di questa energia abbandoni il nucleo, predice le percentuali relative Γ_i/Γ di neutroni, protoni, raggi gamma, ecc. di varie energie che si producono nella reazione. Quando si tenga conto dell'emissione successiva di vari neutroni, le previsioni della teoria statistica composta riproducono i risultati osservati di numerose reazioni nucleari. Pertanto la distribuzione dei prodotti risultanti da una reazione nucleare a nucleo composto fornisce una verifica quantitativa della natura statistica delle interazioni del sistema composto. Un'altra espressione diretta della natura statistica delle interazioni è data dalla distribuzione casuale delle energie e delle larghezze delle risonanze composte osservate nella diffusione di neutroni a bassa energia, di cui si è parlato sopra.

Un'altra classe di reazioni che possono avvenire alle stesse energie delle reazioni con nuclei composti comprende le ‛reazioni dirette', in cui il proiettile, invece di fondersi con il nucleo-bersaglio, riemerge dal bersaglio dopo una o poche interazioni elementari. Queste interazioni possono implicare l'urto tra uno dei nucleoni del proiettile e uno di quelli del bersaglio, la diffusione di un nucleone di uno dei nuclei da parte del potenziale medio dell'altro, oppure l'azione del potenziale medio di un nucleo sulla densità media dei nucleoni dell'altro. Queste interazioni danno luogo a una deviazione del proiettile, spesso unita all'eccitazione di uno stato collettivo nel bersaglio o nel proiettile, all'eccitazione di uno dei nucleoni in uno stato del modello a guscio con energia più alta, al trasferimento di uno o più nucleoni dal bersaglio al proiettile o viceversa o addirittura a una qualche combinazione di questi fenomeni. Le sezioni d'urto di tali reazioni dipendono più fortemente dall'angolo di deviazione del proiettile di quanto non ne dipenda la sezione d'urto delle reazioni composte. Il modo in cui la sezione d'urto varia con l'angolo dipende dal momento angolare che i nucleoni trasferiti possiedono prima e dopo la collisione. Di conseguenza una reazione nucleare diretta può essere usata per determinare il modo in cui i singoli nucleoni si muovono nello stato nucleare prodotto nella reazione. Queste informazioni hanno contribuito molto a farci comprendere la struttura degli stati nucleari complessi in termini del moto dei singoli nucleoni.

I recenti progressi compiuti nella costruzione degli acceleratori di particelle hanno reso possibile l'osservazione delle reazioni che avvengono quando due nuclei complessi si scontrano. In questi casi si sono osservati dei processi che sono stati identificati come reazioni dirette in cui il nucleo proiettile sfiora appena il nucleo bersaglio. Purtroppo per queste reazioni la dipendenza angolare delle sezioni d'urto non è molto sensibile ai dettagli dello stato nucleare eccitato, perché la deviazione del proiettile è causata soprattutto dalla repulsione elettrica cui esso è sottoposto a grandi distanze dal nucleo bersaglio. Sono state anche osservate delle reazioni in cui due nuclei pesanti si fondono e pare che le proprietà del sistema composto risultante siano ben rappresentate dalla teoria statistica. I fenomeni che avvengono in questo caso, tuttavia, sono stati solo in parte studiati sperimentalmente e vi sono indicazioni dell'esistenza di fenomeni che non sembrano rientrare in nessuno dei due schemi di reazione che valgono per le reazioni causate da proiettili più semplici.

7. Disintegrazione beta.

Nelle interazioni nucleari di cui si è trattato nel capitolo precedente i prodotti della reazione hanno un numero di neutroni e protoni pari a quello dei nuclei che hanno dato inizio alla reazione.

Un'importantissima classe di reazioni nucleari in cui questa regola non vale comprende quei fenomeni, chiamati ‛di disintegrazione beta', in cui un neutrone si trasforma in un protone o viceversa. In pari tempo viene emesso o assorbito dal nucleo un elettrone o un positrone - cioè la controparte positiva di un elettrone - di modo che non vi è né creazione né distruzione di carica elettrica. Questo processo di disintegrazione beta avviene spontaneamente in nuclei di tutte le dimensioni, dal neutrone ai nuclei degli elementi transuranici, ogni volta che vi è energia sufficiente per il processo. Sebbene sia impossibile predire con esattezza il momento in cui un dato nucleo emetterà un elettrone, ogni processo di decadimento beta è tuttavia caratterizzato da una vita media T_1/2, cioè dal tempo medio necessario affinché la metà dei nuclei di un campione decada. Questi tempi possono variare da una frazione di secondo sino a molte migliaia di anni, ma anche i più brevi di essi sono molto lunghi rispetto a quelli tipici, compresi tra 10^-18 e 10^-22 secondi, della maggior parte delle altre reazioni nucleari. Le disintegrazioni beta di nuclei con N e Z specifici producono elettroni o positroni con una distribuzione continua di energie, fino a un'energia massima E_max, propria di ogni reazione particolare; normalmente E_max è compresa tra una frazione di MeV e alcuni MeV.

La distribuzione delle energie dei prodotti del decadimento beta ha costituito per lungo tempo un enigma della teoria quantistica del nucleo. Un'ipotesi naturale era quella di supporre che gli elettroni di varie energie corrispondessero a decadimenti beta relativi a stati nucleari d'eccitazione diversi. Per controllarla, fu compiuto un esperimento in cui con un calorimetro si misurava l'energia totale non soltanto degli elettroni del decadimento beta, ma anche quella di tutti i fotoni emessi dai presunti stati nucleari eccitati. L'esperimento, invece, mostrò che non veniva liberata nessuna energia addizionale, all'infuori di quella degli elettroni. Di conseguenza la gamma delle energie degli elettroni non era dovuta alla produzione di una corrispondente gamma di stati nucleari eccitati. Mancava una gran quantità di energia e ci si accorse presto che vi era un difetto anche nel momento della quantità di moto, per un valore pari a ℏ/2. La situazione era talmente singolare che Niels Bohr arrivò addirittura a suggerire l'ipotesi che l'energia e il momento della quantità di moto potessero anche non essere conservati nel processo di decadimento beta. Più tardi, nel 1934, Fermi suggerì una teoria del decadimento beta che, con un'importante modificazione, si è dimostrata adatta a spiegare con grande precisione le proprietà osservate del processo di disintegrazione beta nei nuclei. Seguendo un suggerimento di Pauli, Fermi formulò l'ipotesi che l'energia liberata nella disintegrazione si dividesse tra l'elettrone e un'altra particella, il neutrino, priva di carica e perciò stesso non facilmente osservabile. La disintegrazione avviene quando un nucleone di un tipo si trasforma improvvisamente nel nucleone dell'altro tipo, più un elettrone o un positrone e un neutrino, secondo lo schema delle reazioni seguenti:

p → n + e⁺ + ν

n → p + e^- + ν̄. (12)

Nel linguaggio della meccanica quantistica, l'energia d'interazione è proporzionale al prodotto delle funzioni d'onda del protone, del neutrone, dell'elettrone o positrone e del neutrino. Nel caso in cui un elettrone si combini col nucleo? l'elettrone e il protone spariscono e appaiono invece un neutrone e un neutrino. La rappresentazione quantomeccanica è la stessa: l'interazione è proporzionale al prodotto delle funzioni d'onda del protone, dell'elettrone, del neutrone e del neutrino.

Il neutrino prodotto in una disintegrazione beta porta via non soltanto energia, ma anche momento della quantità di moto, sì che dal confronto tra i momenti angolari dei nuclei prima e dopo il decadimento beta si può concludere che il neutrino deve avere un momento angolare di spin pari a ½ℏ, come quello dell'elettrone. Nel 1938 dall'osservazione delle direzioni dei moti dell'elettrone e del nucleo prodotti in una disintegrazione beta si poté mostrare che al neutrino si deve anche attribuire una quantità di moto. Ma la prova definitiva dell'esistenza del neutrino fu resa possibile per la prima volta nel 1953, quando Reines e Cowan posero vicino a un reattore nucleare un contatore a scintillazione, schermato completamente da tutte le altre particelle prodotte dalle reazioni che avvenivano all'interno del reattore. Essi furono in grado di determinare che, in certi casi, quando un neutrino colpiva uno dei protoni del materiale del contatore, si aveva la produzione di un neutrone e di un positrone. Essi trovarono anche che la sezione d'urto per questo processo è di circa 10^-43 cm², il che significa che un neutrino dovrebbe essere in grado di penetrare attraverso uno spessore di 10¹⁴ km di materia.

Le grandezze più facilmente misurabili di una reazione di disintegrazione beta sono la vita media e le quantità di moto degli elettroni e dei positroni prodotti. Lo spettro delle quantità di moto può essere facilmente calcolato sulla base della teoria di Fermi; le distribuzioni osservate sperimentalmente si accordano bene con i calcoli teorici (v. fig. 23). La caratteristica principale degli spettri è data dall'energia massima E_max che possono avere l'elettrone o il positrone. Un elettrone di energia E_max è accompagnato dalla produzione di un neutrino privo di energia cinetica, mentre invece, quando si verifica la produzione di elettroni di energia minore, ciò significa che l'elettrone ha diviso l'energia disponibile con il neutrino. Accurati studi dello spettro elettronico per energie vicine a E_max hanno dimostrato che la massa di riposo del neutrino è probabilmente nulla e comunque certamente inferiore a un millesimo della massa di riposo dell'elettrone. Quindi un neutrino privo di energia cinetica non possiede alcuna energia e la somma dell'energia massima E_max dell'elettrone e dell'energia dello stato nucleare prodotto dalla disintegrazione deve essere uguale all'energia del nucleo prima della sua disintegrazione. Per esempio, il ¹²B, un nucleo con 5 protoni e 7 neutroni, ha una vita media T_1/2 = 0,02 secondi, prima di disintegrarsi con un decadimento beta in un normale nucleo ¹²C di carbonio con 6 protoni e 6 neutroni. L'energia cinetica massima dell'elettrone emesso è di 13,4 MeV, di modo che l'energia totale dell'elettrone, comprensiva cioè della sua energia di riposo di 0,5 MeV, ha un valore massimo E_max = 13,9 MeV. Il nucleo ¹²B deve quindi avere un'energia totale di 13,9 MeV maggiore di quella del nucleo ¹²C. Di questa differenza, 1,3 MeV sono dovuti al fatto che il neutrone che sparisce dal nucleo ¹²B ha una massa di riposo maggiore del protone che appare nel nucleo ¹²C, cosicché la differenza tra le energie di legame di ¹²B e ¹²C è di 12,6 MeV. Questo valore concorda esattamente con l'energia calcolata in base alla liberazione di energia nelle reazioni nucleari (coinvolgenti particelle pesanti) che portano alla formazione di ¹²B e ¹²C. Circa una volta su quaranta la disintegrazione di ¹²B produce un nucleo ¹²C in uno dei suoi stati eccitati invece che in quello fondamentale e vi sono anche alcune disintegrazioni beta - per esempio quella del ⁶⁰Co - che producono sempre uno stato eccitato del nucleo risultante.

Una teoria particolareggiata del processo di decadimento beta deve includere il prodotto delle funzioni d'onda delle particelle coinvolte. Tali funzioni d'onda devono descrivere non soltanto le posizioni, ma anche i momenti di spin delle particelle. Nella meccanica quantistica relativistica si possono classificare le possibili combinazioni dei ‛prodotti' delle posizioni e degli spins che soddisfano le condizioni di invarianza di Lorentz. I nucleoni di un nucleo hanno un'energia cinetica molto minore della loro energia di riposo, sì che possono essere trattati in maniera non relativistica. In questa approssimazione i vari ‛prodotti' possono essere classificati a seconda che il nucleone prodotto abbia spin parallelo o antiparallelo a quello del nucleone che si disintegra. Le disintegrazioni beta in cui la direzione dello spin del nucleone rimane invariata vengono chiamate ‛transizioni di Fermi', mentre quelle in cui lo spin del nucleone inverte la sua direzione vanno sotto il nome di ‛transizioni di Gamow-Teller'. Le transizioni possono essere ulteriormente classificate secondo le relazioni intercorrenti tra spins e quantità di moto dell'elettrone e del neutrino. Osservando la correlazione tra spin e quantità di moto dell'elettrone prodotto nel decadimento beta del ⁶⁰Co, un gruppo di sperimentatori, sotto la direzione di Wu, dimostrò nel 1956 che l'interazione fondamentale del decadimento beta può distinguere la sinistra dalla destra; questo risultato inatteso ha avuto delle importanti conseguenze nella teoria delle particelle elementari. Tuttavia la maggior parte degli esperimenti in fisica nucleare non è sensibile alla direzione degli spins degli elettroni e dei neutrini e di conseguenza nella maggior parte dei problemi di fisica nucleare è importante soltanto distinguere tra le interazioni di Fermi e quelle di Gamow-Teller.

Proprio come nel caso dell'emissione della luce, l'emissione beta di elettroni o positroni e neutrini avviene con probabilità molto più alta quando le particelle emesse non hanno alcun momento della quantità di moto all'infuori di quello dovuto ai loro spins intrinseci. Questi processi di emissione prendono il nome di ‛transizioni permesse', mentre le altre vengono chiamate ‛proibite', perché avvengono molto più raramente. Sono state formulate alcune regole di selezione per individuare le transizioni permesse. Una transizione di Fermi permessa può solamente produrre un nucleo con lo stesso momento della quantità di moto di quello originale, perché gli spins dell'elettrone e del neutrino sono diretti in verso opposto, di modo che il momento angolare risultante è nullo. Invece una transizione di Gamow-Teller permessa può anche produrre un nucleo con un momento ℏ della quantità di moto in più o in meno rispetto a quello del nucleo iniziale, perché gli spins dell'elettrone e del neutrino sono rivolti nello stesso verso ed hanno quindi un momento angolare risultante pari ad ℏ. Questo momento della quantità di moto può anche essere dovuto a una riorientazione della direzione del momento del nucleo, di modo che il modulo di questo può anche conservarsi in una transizione di Gamow-Teller.

Dalla vita media T_1/2 osservata nelle disintegrazioni beta si possono anche ricavare delle informazioni sulle relazioni esistenti tra le strutture del nucleo disintegrato e quelle del nucleo prodotto. Per prima cosa la vita media deve essere moltiplicata per un fattore f che può essere ricavato dalla teoria del decadimento beta e che dipende principalmente dalla differenza tra le energie di legame dei due stati nucleari. La vita media così corretta, chiamata ft, dipende allora solo dalla struttura degli stati nucleari interessati. Per esempio, il valore di ft per transizioni di Fermi permesse dipende soltanto dagli spins isobarici dei nuclei. I valori di ft per transizioni di Gamow-Teller sono invece più complicati da interpretare, dal momento che lo spin del nucleone che decade cambia verso; tuttavia possono essere calcolati anche con l'aiuto di modelli nucleari come quello a guscio o quello collettivo. In particolare, i rapporti fra i valori di ft per disintegrazioni che producono stati collettivi diversi dello stesso nucleo hanno offerto una preziosa conferma della struttura di tali stati.

Le vite medie lunghe, tipiche di nuclei instabili rispetto al processo beta, permettono di studiare il comportamento di tali nuclei negli atomi e nelle molecole che formano, così come è possibile studiare quello dei nuclei stabili. Per esempio, si è visto che due atomi di ³H, ossia di trizio, possono formare una molecola che ha la stessa energia di legame e gli stessi stati eccitati di una normale molecola di idrogeno ¹H, eccetto che per gli effetti della diversa massa nucleare. Nello spettro degli stati eccitati della molecola di trizio, alcuni stati rotazionali non sono visibili perché le loro funzioni d'onda non sarebbero antisimmetriche nelle coordinate dei due nuclei di trizio. Ciò dimostra che i due nuclei di trizio sono completamente identici sotto ogni punto di vista, perché altrimenti non vi sarebbe alcun motivo perché la funzione d'onda della molecola fosse antisimmetrica. Anche in tal modo, però, i due nuclei di trizio possono non decadere contemporaneamente, il che offre un forte argomento a favore dell'interpretazione ortodossa della meccanica quantistica della Scuola di Copenhagen: il processo quantistico del decadimento beta è effettivamente dominato dalle leggi della probabilità. Se esistesse qualche differenza, ancora non osservata, tra i due nuclei di trizio, che determinasse quale dei due deve decadere per primo, essa comporterebbe uno spettro di stati della molecola completamente diverso.

Applicazioni. - Fatta eccezione per questo effetto di antisimmetria e per la diversità della loro massa, i nuclei beta attivi si comportano chimicamente come gli isotopi stabili del corrispondente elemento. La facilità con la quale se ne può rivelare la presenza mediante un contatore a scintillazione ha portato ad applicazioni molto utili in vari campi di ricerca. Per esempio, attraverso le quantità relative dell'isotopo ¹⁴C, che decade con un processo beta dopo una vita media di 5.600 anni, è possibile determinare l'età di un campione di materia organica: infatti, in un campione vecchio rispetto a un campione più recente, una minore percentuale degli atomi di carbonio è costituita da ¹⁴C, perché molti dei nuclei ¹⁴C che erano originariamente presenti nel campione vecchio hanno subito una disintegrazione beta. Questo metodo è stato impiegato nella datazione di un gran numero di reperti archeologici. Su una scala temporale più lunga, possono essere datati campioni di roccia contenenti nuclei alfa radioattivi, misurando il rapporto tra la quantità di residui del processo di disintegrazione e il numero di nuclei non disintegrati che ancora rimangono. Nella ricerca biologica si può facilmente osservare la velocità con la quale un organismo assorbe e distribuisce un composto chimico, ‛marcando' il composto, cioè sostituendo uno dei suoi atomi con un isotopo radioattivo del medesimo elemento. Questa tecnica è stata adoperata per studiare i processi metabolici di molte piante e animali ed è molto usata per diagnosticare i tumori, il cui metabolismo anormale può spesso essere rivelato in questo modo. La possibilità di osservare una differenza tra atomi dal comportamento chimico identico si è anche dimostrata utile per lo studio della struttura chimica di una singola cellula e del codice genetico.

8. Fissione.

Poiché la forza nucleare dovuta allo scambio di mesoni tra nucleoni agisce principalmente tra nucleoni vicini, ogni nucleone di un nucleo grande è soggetto pressappoco alla stessa forza attrattiva di un nucleone in un nucleo piccolo, a parte il fatto che quello nel nucleo grande viene a trovarsi più raramente nella regione superficiale. Tuttavia la repulsione elettrica tra protoni si fa sentire in maniera efficace in tutto il nucleo, per cui in un nucleo pesante ogni protone è soggetto alla repulsione elettrica di tutti gli altri protoni, così che la forza elettrica, benché sia per sua natura molto più debole di quella nucleare, contribuisce in modo piuttosto rimarchevole all'energia di legame dei nuclei pesanti. Come si può vedere dalla fig. 2, i nucleoni nei nuclei con più di un centinaio di nucleoni avrebbero un'energia di legame maggiore se il nucleo grande fosse diviso in due frammenti minori, in modo che ogni protone dovesse subire la repulsione elettrica soltanto della metà dei rimanenti protoni. Tale divisione di un nucleo pesante in due frammenti più leggeri viene detta fissione. L'energia di legame addizionale ottenuta dai nucleoni quando un nucleo pesante si divide è sufficiente per imprimere ai nucleoni una velocità pari a circa 0,04 volte quella della luce.

Nonostante l'enorme vantaggio energetico della divisione in frammenti, i nuclei con un numero di nucleoni che va da 100 a 230 non sembra che fissionino spontaneamente. La ragione di questo fatto è che nel processo di divisione dev'esserci uno stadio intermedio in cui il nucleo assume una forma allungata, come quella di fig. 24. In questo stadio i protoni non sono molto più lontani di quanto non lo fossero all'inizio, per cui gli effetti della repulsione elettrica non sono molto ridotti. D'altra parte, però, molti più nucleoni vengono a trovarsi nelle regioni superficiali dove non possono ricavare tutto il beneficio dalle forze nucleari attrattive, cosicché, quando i nucleoni si trovano in questa configurazione intermedia, sono meno strettamente legati. Se non possiede l'energia necessaria per assumere questo stadio intermedio, il nucleo non può dividersi se non per mezzo di un processo a tunnel, tipicamente quantistico (v. cap. 6). La barriera energetica che rappresenta le configurazioni intermedie non favorevoli è talmente larga e alta che i nuclei ordinari dovrebbero attendere un tempo pari a varie volte l'età dell'universo prima di potersi dividere. Ma per i nuclei pesanti la repulsione elettrica è talmente forte che neppure le configurazioni intermedie della fig. 24 sono troppo sfavorevoli e per i nuclei con più di 230 nucleoni esiste effettivamente la possibilità della fissione spontanea. Soltanto per pochi nuclidi si è osservata la fissione spontanea, con vite medie che vanno da un paio di ore a molti miliardi di anni: per esempio, nel caso dell'²³⁸U, la vita media è di circa 10¹⁶ anni. I nuclidi con A minore di 230 fissionano troppo lentamente per poter essere osservati, mentre la maggior parte di quelli più pesanti è più facilmente soggetta ad altri processi, quali la disintegrazione beta o alfa, che alla fissione.

La difficoltà di penetrare attraverso la barriera di potenziale della configurazione intermedia, che rende assai poco frequente la fissione spontanea, è di gran lunga ridotta se un nucleo pesante viene fornito di un'energia di eccitazione uguale o maggiore di quella della barriera. Questa energia può essere fornita da un quanto di luce di energia sufficiente o da un neutrone. Se la reazione è innescata da un neutrone, non soltanto la sua energia cinetica, ma anche quella dovuta all'attrazione del nucleo divengono disponibili per aiutare il nucleo a fissionare. Per alcuni nuclei, in particolare ²³³U, ²³⁵U e ²³⁹Pu, la sola energia di legame del neutrone è sufficiente per la fissione del sistema neutrone-nucleo; perfino la cattura di un neutrone privo di energia cinetica può, quindi, dare inizio alla fissione. Altri nuclei fissioneranno rapidamente soltanto se il neutrone possiede almeno 1 MeV di energia cinetica: esempi importanti di questa classe sono i nuclidi naturalmente abbondanti ²³²Th e ²³⁵U.

Quindi, soprattutto per i nuclei pesanti, la reazione di fissione si può aggiungere alla lista delle altre reazioni innescate dai neutroni, comprendente già l'emissione di fotoni e la diffusione elastica e anelastica. Dipenderà in maniera sensibile dall'energia cinetica del neutrone, e anche dai valori N e Z del nucleo pesante, quale di questi processi avverrà con maggior frequenza quando un neutrone urta un nucleo. La sezione d'urto per una reazione di fissione indotta da un neutrone può essere molto grande, soprattutto se la fissione è causata da un neutrone lento, nel qual caso essa non è limitata all'area del nucleo, ma cresce proporzionalmente alla lunghezza d'onda di de Broglie del neutrone incidente. Per esempio, un neutrone di energia cinetica di 2,5•10^-8 MeV (pari a quella posseduta dalle molecole di un gas a temperatura normale) produce la fissione di un nucleo di ²³U con una sezione d'urto di 60.000 F², cioè cento volte maggiore dell'area della superficie del nucleo.

Quando un nucleo pesante subisce una fissione, esso si divide generalmente in due frammenti di dimensioni disuguali e in un certo numero di neutroni. Le dimensioni dei due frammenti variano da caso a caso, ma di solito in un frammento vanno circa i 3/5 dei nucleoni e nell'altro i rimanenti 2/5. Questi frammenti sono prodotti in stati altamente eccitati, nei casi tipici con un'eccitazione di circa 10 MeV ciascuno, per cui, dopo essersi separati, essi decadono nel loro stato fondamentale emettendo raggi gamma e neutroni. Poiché le forze elettriche sono più deboli in questi frammenti leggeri che nel nucleo originale pesante, i nuclei leggeri tendono ad avere globalmente più protoni e meno neutroni del loro progenitore. Benché abbiano perduto alcuni neutroni mentre si trovavano allo stato eccitato, i frammenti non sono ancora beta stabili e alla fine si disintegrano emettendo elettroni e neutrini. La maggior parte dei 200 MeV di energia liberata nel processo di fissione appare, tuttavia, come energia cinetica dei frammenti della fissione, i quali si allontanano molto rapidamente gli uni dagli altri a causa della forte repulsione elettrostatica esistente fra loro. Questa energia viene rapidamente trasformata in calore a causa delle collisioni tra i frammenti della fissione è gli atomi che si trovano nelle vicinanze. I prodotti di una reazione di fissione sono costituiti dunque da due frammenti, da un certo numero di elettroni e di fotoni, da una gran quantità di calore e da alcuni neutroni di energia cinetica di circa 2 MeV. Il numero medio di neutroni prodotti, di solito indicato con v, svolge un ruolo primario nell'applicazione della fissione ai processi di reazione a catena. Nella maggior parte dei processi, ν è di circa 2 o 3 neutroni per fissione, ma il suo valore cresce leggermente al crescere della velocità del neutrone che dà inizio alla reazione.

L'interpretazione teorica del processo di fissione si basa sul lavoro compiuto nel 1939 da Bohr e Wheeler, i quali si avvalsero del modello a goccia liquida del nucleo (v. cap. 2) per valutare l'energia necessaria per deformare un nucleo pesante fino a fargli raggiungere le configurazioni illustrate nella fig. 24. Essi identificarono l'energia massima richiesta con quella minima occorrente per indurre il nucleo a fissionare. Avvalendosi della teoria del nucleo composto, Bohr e Wheeler riuscirono a ottenere una relazione quantitativa tra le energie di queste configurazioni e la sezione d'urto per la fissione indotta. Gli studi successivi furon volti a cercare di comprendere meglio la struttura e l'energia delle configurazioni intermedie che portano alla fissione; per tali studi si è reso indispensabile l'impiego di grossi calcolatori elettronici.

La forma della barriera di potenziale nella fissione è dovuta agli effetti contrastanti della riduzione di repulsione elettrica quando il nucleo pesante si divide in due pezzi e della diminuzione del legame nucleare dovuta all'incremento del numero di particelle vicine alla superficie del nucleo. Ma questi due effetti si elidono quasi completamente - come invero è d'uopo perché vi sia una probabilità di fissione - di modo che altri effetti minori possono avere una grande influenza sul processo di fissione. Un ruolo particolarmente importante sembra avere il modo in cui variano le energie delle singole particelle del modello a guscio con la deformazione. Strutinsky di recente ha sviluppato un metodo che tiene conto di questo fatto ed ha dimostrato che una struttura che rassomigli a un guscio chiuso può rendere stabile una configurazione in cui il nucleo che si divide sia molto più lungo che largo. Le prove dell'esistenza di queste configurazioni stabili sono date dalle sezioni d'urto per fissione indotta da neutroni e si è visto che i nuclei che fissionano possono rimanere in queste configurazioni per tempi anche dell'ordine di 10^-2 secondi. Uno stato molto elongato e a lunga vita di questo tipo si chiama isomero di forma. Gli effetti di guscio nella struttura a particella singola sembrano poter anche fornire una spiegazione del fatto che (eccetto che per il caso di energie di eccitazione molto alte) i frammenti prodotti nella fissione sono generalmente di dimensioni disuguali: man mano, cioè, che il nucleo si allunga, oltre alla configurazione stabile a guscio, sono possibili delle configurazioni più vantaggiose a particella singola in cui un'estremità del nucleo che si divide diviene più grande dell'altra. Anche se il guadagno energetico è piccolo, esso può essere sufficiente per far sì che il nucleo si divida in parti disuguali, specialmente quando l'energia è scarsa.

La tavola periodica dei nuclei che si trovano in natura o che sono stati sintetizzati è limitata ai nuclei con Z inferiore a 104 e ciò soprattutto perché un nucleo con una carica elettrica maggiore sarebbe sottoposto a fissione in maniera talmente rapida da non poter essere osservato. Un'eccezione a questa regola potrebbe, però, derivare dalla proprietà di un guscio chiuso di rendere stabile una configurazione nucleare di forma particolare. Sulla base di calcoli teorici si è visto che un nucleo con 114 protoni e 184 neutroni sarebbe ‛doppiamente magico': sia il numero di protoni, cioè, sia quello di neutroni sarebbero sufficienti per occupare tutti gli stati a particella singola di un guscio maggiore. Un guscio doppiamente magico di questo tipo sarebbe eccezionalmente stabile rispetto a deformazioni che ne alterassero la forma sferica e di conseguenza la sua vita media per fissione potrebbe essere abbastanza lunga da essere osservabile. Tuttavia questo strano nucleo non è ancora stato visto perché è molto difficile da sintetizzare, ma è certo che la sua osservazione e lo studio delle sue proprietà costituirebbero una conferma interessante delle teorie che ne predicono l'esistenza.

Applicazioni. - La reazione di fissione indotta da neutroni si è dimostrata particolarmente utile per le applicazioni tecnologiche, in quanto non produce soltanto energia, ma anche più neutroni di quanti ne occorrano per innescarla ; è per questo che, in condizioni favorevoli, i neutroni prodotti dalla fissione di un nucleo possono dare inizio a ulteriori reazioni di fissione nei nuclei vicini. Questo processo può essere reso autosufficiente, nel qual caso prende il nome di reazione a catena e gli apparecchi che rendono possibile il ripetersi per lungo tempo di reazioni di fissione sono chiamati ‛reattori nucleari' (v. nuclei atomici: Reattori nucleari).

I reattori nucleari sono utili per molti scopi. Come strumenti di ricerca, essi producono neutroni in grandi quantità per le esperienze relative allo studio non soltanto della struttura nucleare, ma anche della struttura atomica dei solidi. I neutroni possono essere impiegati anche per dare inizio a reazioni nucleari che producono isotopi radioattivi, utili per la ricerca (v. cap. 7). I frammenti che provengono direttamente dal processo di fissione sono anche isotopi radioattivi che possono essere tolti dal reattore e utilizzati.

Tra i prodotti più importanti delle reazioni indotte dai neutroni nei reattori vi è l'elemento ²³⁹Pu, che non si trova in natura perché il suo tempo di dimezzamento, prima di decadere con emissione di una particella alfa, è di soli 20.000 anni. Il ²³⁹Pu può essere facilmente prodotto per irradiazione da neutroni dell'²³⁸U, che è invece abbondante nella crosta terrestre. La ragione per cui si desidera produrre il ²³⁹Pu è che, al pari dell'²³⁵U e contrariamente all'²³⁸U, esso fissiona per urto di neutroni lenti. Poiché la fissione si produce più facilmente per assorbimento di neutroni di bassa che non di alta energia, la maggior parte dei reattori contiene dei ‛moderatori' o sostanze come la grafite e l'acqua che rallentano i neutroni prima che questi diano luogo a reazioni diverse dalla fissione. Perciò in un reattore che usi come combustibile l'uranio naturale la maggior parte dei nuclei fissili è costituita da ²³⁵U, anche se questo isotopo costituisce meno dell'uno per cento dell'uranio naturale. Si può costruire un reattore molto più efficiente e compatto se il combustibile contiene un'alta percentuale di nuclei che possono venir scissi da neutroni lenti. La separazione dell'²³⁵U dall'²³⁸U è assai costosa, perché i due isotopi sono chimicamente identici, mentre il ²³⁹Pu, essendo un elemento chimico diverso, può essere facilmente separato dal suo genitore, l'²³⁸U. La produzione del ²³⁹Pu è dunque un esempio di come un reattore possa essere usato per produrre combustibile di buona qualità per un altro reattore. Ciò nonostante, la maggior parte dei reattori di potenza già in funzione o in costruzione usa l'²³⁵U come nuclide fissile. Sebbene nel 1940 il problema fosse sembrato quasi insuperabile, è stato in seguito sviluppato un metodo molto efficiente che, con l'aiuto di particolari pompe, permette di separare i due isotopi dell'uranio mediante la diffusione del gas UF₆ attraverso delle barriere di metallo poroso. Questo metodo di separazione funziona così bene che la United States Atomic Energy Commission vende l'²³⁵U a circa 12 dollari il grammo, assai di meno del Pu. Sono stati anche sviluppati, sia pure ancora solo parzialmente, altri metodi di separazione.

Anche l'energia termica che si libera in una reazione di fissione può essere utilizzata. Per fare questo, il calore deve prima essere trasportato dall'interno del reattore in un posto in cui possa essere trasformato in energia elettrica o meccanica: a tale scopo, si fa circolare attraverso di esso un fluido come l'acqua, l'aria o il sodio liquido. Tuttavia il liquido di raffreddamento e i tubi che lo contengono, così come il moderatore, di cui abbiamo parlato prima, non devono assorbire troppi neutroni, altrimenti non ne resterebbero a sufficienza per continuare la reazione a catena. Il sistema di raffreddamento e tutte le altre strutture meccaniche all'interno del reattore devono essere progettate tenendo presente questo e allo stesso tempo anche il fatto che esse devono poter sostenere, senza indebolirsi, elevate temperature e grandi quantità di radiazioni neutroniche e gamma. Inoltre, il reattore deve essere circondato da schermi di protezione capaci di assorbire quasi tutti i neutroni, i raggi gamma, gli elettroni e le altre radiazioni generate nel reattore, nocive per gli organismi viventi. Tutte le parti del reattore devono essere progettate in maniera tale da impedire la fuga di materiale radioattivo, anche nel caso di cattivo funzionamento di qualche componente del reattore. Nel caso dei reattori di potenza, sorge il problema di eliminare le scorie contenenti i frammenti di fissione. Ancora non si è trovato il modo di utilizzarle nelle quantità in cui vengono prodotte e, a causa della lenta natura del processo di disintegrazione beta, esse continuano a essere radioattive per anni.

Un reattore nucleare deve contenere anche un meccanismo che impedisca alla reazione a catena di procedere con troppa rapidità. Se si vuole che la temperatura del reattore rimanga costante, i neutroni prodotti da ogni fissione devono, in media, dare inizio esattamente a un nuovo processo di fissione. Nel linguaggio tecnico, questa condizione si esprime dicendo che ‛la reattività deve essere uguale a uno'. Essa può essere soddisfatta inserendo nel reattore una o più aste di controllo (contenenti materiali come il cadmio, il boro o una terra rara, che assorbono fortemente i neutroni lenti), la cui posizione viene regolata meccanicamente, da un operatore o automaticamente, in modo da mantenere la reattività esattamente uguale a uno. Oltre ad essere impiegate per le regolazioni rapide, da effettuare entro pochi secondi o minuti, queste aste di controllo devono anche essere spostate lentamente entro periodi di tempo di qualche mese per compensare la combustione del materiale fissile.

Vi sono due caratteristiche che contribuiscono grandemente alla stabilità dei reattori nucleari. Una di queste è l'espansione termica delle componenti del reattore dovuta al riscaldamento per un aumento temporaneo della potenza prodotta: con l'espansione del reattore, un numero maggiore di neutroni sfugge e la reattività decresce. L'altra caratteristica stabilizzante è il fatto che una frazione, compresa tra 0,4 e 1%, dei neutroni viene emessa dopo la fissione con un certo ritardo, contenuto tra un secondo e un minuto circa, il che significa che il reattore risponderà solo con lentezza alle variazioni di reattività ed è dunque facilmente controllabile.

Quando è stata consumata una quantità sufficiente di combustibile, una parte di quello già utilizzato viene estratta dal reattore e sostituita con del combustibile nuovo. Il reattore è costruito in modo tale che questo procedimento di ricarica si renda necessario solo a intervalli abbastanza lunghi, che vanno da qualche mese sino anche a due anni. Il combustibile già sfruttato viene quindi generalmente immesso in un grosso serbatoio pieno d'acqua dove perde la sua radioattività e dissipa il calore. Dopo vari mesi di questo raffreddamento, il combustibile viene trasportato in un impianto dove è sottoposto a un procedimento chimico mediante il quale l'uranio o il plutonio residuo viene separato dai prodotti della fissione che, se lasciati nel reattore, assorbirebbero neutroni e farebbero diminuire la reattività. Se l'isotopo fissile è l'²³⁵U, l'uranio dovrà di solito essere nuovamente arricchito per separazione isotopica.

La produzione industriale di energia nucleare cominciò a svilupparsi negli anni cinquanta ed è ora in un periodo di rapida espansione. Nel 1972 negli Stati Uniti, su una potenza elettrica installata totale di 300 milioni di chilowatt, circa 1 4 milioni erano di origine nucleare e si prevede che nel 2000 la potenza elettrica nucleare installata sarà, sempre negli Stati Uniti, di circa 800 milioni di chilowatt.

Uno stimolo alla costruzione di impianti di potenza nucleare è costituito dalla diminuzione delle riserve di combustibile fossile e specialmente di petrolio. Il carbone, benché sia ancora abbondante in molti paesi, potrà in futuro essere utilizzato quasi esclusivamente per la produzione artificiale di gas illuminante. L'uranio sarà ancora abbondante per molti anni; tuttavia, fino a che verrà usato solo l'isotopo ²³⁵U, l'utilizzazione del grezzo non sarà completa; per questo in vari paesi si stanno compiendo degli ingenti sforzi per costruire un reattore ‛autofertilizzante', nel quale, cioè, si formi più ²³⁹Pu (mediante assorbimento di neutroni da parte dell'²³⁸U) di quanto ne venga consumato nella fissione.

È anche possibile costruire dei congegni in cui la reazione nucleare a catena non avvenga in maniera lenta e uniforme, ma aumenti rapidamente fino al raggiungimento di una velocità di reazione altissima, alla quale l'energia ottenuta sia liberata sotto forma di esplosione. La forza di una tale esplosione è talmente grande confrontata con l'energia che può essere liberata da una quantità trasportabile di esplosivi chimici, che le bombe a fissione hanno assunto un ruolo di primo piano come armi militari.

Le prime bombe a fissione, sganciate su Hiroshima e Nagasaki, posero fine alla guerra tra Giappone e Stati Uniti ed è in gran parte per questo che i governi hanno da allora finanziato la fisica nucleare e le sue applicazioni per scopi civili e militari. Sia gli Stati Uniti sia l'Unione Sovietica hanno costruito grandi arsenali di armi a fissione (si veda anche la discussione sulle armi termonucleari nel capitolo seguente), ma anche altre tre potenze, la Repubblica Popolare Cinese, la Francia e il Regno Unito, dispongono di tali armi in quantità considerevoli (v. armamenti; v. nuclei, atomici: Armi nucleari).

9. Fusione.

In teoria la maniera più ovvia per sfruttare l'energia connessa con le intense forze interagenti tra i nucleoni è quella di costruire dei nuclei di peso medio partendo da elementi costitutivi più leggeri. Per nuclei con meno di cinquanta nucleoni circa l'energia di legame per nucleone cresce con la dimensione del nucleo, di modo che, quando due nuclei si combinano per formarne uno più pesante, viene liberata energia. Questo processo di combinazione è detto di ‛fusione'.

Perché avvenga una reazione di fusione, i due nuclei leggeri devono urtarsi con velocità notevole, altrimenti la repulsione dovuta alla loro carica elettrica impedisce loro di avvicinarsi tanto da permettere alle forze nucleari di avere effetto. Anche nel caso di una collisione tra due nuclei con un protone ciascuno non c'è praticamente alcuna probabilità che si produca una reazione, a meno che le particelle non abbiano un'energia cinetica superiore a circa 0,01 MeV. Nuclei leggeri con un'energia cinetica di quest'ordine si trovano nelle regioni centrali delle stelle, dove le temperature sono alte proprio in virtù del fatto che viene generata energia mediante reazioni di fusione. Un'energia cinetica media di 0,01 MeV corrisponde a una temperatura di circa 10⁸K. Le collisioni tra nuclei con un maggior numero di protoni richiedono energie cinetiche ancora maggiori. Poiché le reazioni di fusione che si producono nelle stelle vengono iniziate dai nuclei nel gas caldo, esse sono dette reazioni termonucleari. In un gas caldo, la cui temperatura sia T, il numero di atomi, o meglio di nuclei, che ha una velocità compresa tra v e v % dv è dato dalla distribuzione di Boltzmann

e-^mv2/2kT v²dv. (13)

La probabilità che due nuclei con cariche Z₁e e Z₂e e con velocità relativa v, relativamente bassa, penetrino nella barriera di potenziale l'uno dell'altro è data da

e^-2Z1Z2e2/hv. (14)

Il prodotto delle due probabilità (13) e (14) ha un massimo quando l'energia cinetica media di un atomo è compresa tra 5 e 20 volte il valore di kT. Per questo la fusione, nelle stelle, può verificarsi a temperature di 10 milioni di gradi, anziché di 100 milioni.

In un certo senso tutta l'energia utilizzata sulla Terra è prodotta per fusione, dal momento che essa proviene dalle reazioni di fusione che si verificano nel Sole. Le reazioni di fusione che liberano maggiore energia sono quelle che portano alla produzione di ⁴He partendo da protoni (o dall'incorporazione di nucleoni in nuclei più pesanti), perché l'energia di legame per nucleone in un nucleo di elio è già circa pari all'80⁰/₀ del valore massimo che si ha per un nucleo di ferro. Questa energia può essere liberata secondo due principali catene di reazioni. La prima s'inizia con la combinazione di due protoni che formano un deutone, emettendo un positrone e un neutrino. Anche se i due protoni hanno energia sufficiente per avvicinarsi e per interagire, la reazione procede molto lentamente perché consiste in una specie di disintegrazione beta: il protone deve infatti trasformarsi in neutrone. La reazione non può avvenire in due stadi perché due protoni non si attraggono abbastanza per formare uno stato legato. Dopo la formazione del deutone, quest'ultimo può catturare un altro protone per formare, liberando energia, un nucleo di ³He. Ulteriore energia si libera se l'³He urta contro un altro nucleo di ³He e gli sottrae un neutrone, formando così un nucleo stabile di ⁴He e liberando due protoni. La sequenza delle reazioni è dunque la seguente:

¹H + ¹H = ²H + e⁺ + ν (15a)

²H + ¹H = ³He + γ (15b)

2 ³He = ⁴He + H + H (15c)

(e⁺ positrone, ν = neutrino, γ = raggio gamma = radiazione elettromagnetica). Ad alte temperature la reazione (15c) può essere sostituita da altre reazioni. Sono stati fatti dei tentativi per osservare i neutrini emessi in alcune di queste reazioni, ma, finora, essi non hanno avuto successo.

La seconda sequenza di reazioni nucleari che avviene nelle stelle utilizza il carbonio come catalizzatore per fondere insieme i protoni in nuclei di ⁴He. La sequenza delle reazioni è la seguente:

Fisicamente la catena può essere descritta in questo modo: un protone si combina con un nucleo di carbonio, dopo di che può subire un decadimento beta e diventare un neutrone. Il nucleo di carbonio possiede ora un neutrone in più e cattura ancora due protoni uno dopo l'altro; in seguito, attraverso un'altra disintegrazione beta, un altro protone si trasforma in neutrone. Nell'ultimo passaggio un protone urta questo aggregato e porta via con sé i tre nucleoni per formare un nuovo nucleo di ⁴He lasciando dietro di sé il carbonio. A ogni stadio del processo si libera energia quando i nuovi nucleoni si combinano in nuclei. Quest'ultimo processo richiede temperature leggermente più elevate dell'altro in cui i protoni si combinano senza catalisi, perché inizialmente i protoni devono avere energia cinetica sufficiente per superare la repulsione elettrica di tutti e sei i protoni del nucleo di carbonio. La temperatura del Sole è però tale che ambedue i processi contribuiscono alla produzione di energia, anche se è preponderante il contributo dato dalle reazioni della prima sequenza.

La frequenza con cui sono presenti, nella crosta terrestre, gli elementi leggeri, ha indotto a compiere degli sforzi considerevoli per trovare dei sistemi che utilizzino le reazioni di fusione per produrre energia, anche se su una scala più modesta di quella su cui si produce nel Sole. Il requisito che la reazione avvenga alla temperatura più bassa possibile ci obbliga a considerare solo le reazioni tra gli isotopi dell'idrogeno, poiché i nuclei con un maggior numero di protoni si respingono più fortemente e richiedono quindi delle energie cinetiche maggiori per dare inizio alle reazioni. Poiché le interazioni di decadimento beta che trasformano protoni in neutroni hanno delle sezioni d'urto molto piccole, si deve cominciare con uno degli isotopi pesanti dell'idrogeno. Uno di questi è il deuterio, ²H, che si trova con una certa abbondanza in natura e che può essere estratto dall'acqua normale a costi moderati. La fusione del deuterio contenuto in un litro d'acqua di mare libererebbe più energia della combustione di 100 litri di petrolio. Il terzo isotopo dell'idrogeno, l'³H o trizio, decade con un procedimento beta con una vita media di circa 10 anni, così che non si trova in quantità apprezzabili in natura. Esso può tuttavia essere prodotto partendo dal ⁶Li metallico mediante bombardamento di neutroni. Le reazioni più probabili che possono risultare dalla collisione di due nuclei di deuterio sono la produzione di un nucleo di ³He o di ³H, accompagnata dalla liberazione di un protone o di un neutrone. Le sezioni d'urto di queste reazioni sono, tuttavia, molto più piccole di quelle necessarie perché un nucleo di trizio si fonda con uno di deuterio formando ⁴He e un neutrone. Perciò quest'ultima reazione è quella più usata nella costruzione della bomba H, la quale rappresenta finora l'unica utilizzazione dell'energia sviluppata dalle reazioni di fusione. In questa bomba l'alta temperatura richiesta per dare inizio alla reazione di fusione è prodotta dall'esplosione di una bomba a fissione; i nuclei di deuterio e di trizio possono allora fondersi, liberando così ancora più energia di quella prodotta dalla bomba a fissione. Il potere esplosivo delle armi a fusione viene comunemente misurato in megatoni, essendo un megatone pari all'energia liberata dall'esplosione di un milione di tonnellate di tritolo, ossia circa 10¹⁵ joule. Tutte e cinque le potenze nucleari hanno collaudato armi termonucleari dell'ordine di un megatone e alcune di queste hanno costruito bombe con un'energia di qualche diecina di megatoni. Ognuno dei circa duemila missili a lungo raggio posseduti dagli Stati Uniti e dall'Unione Sovietica trasporta una testata di capacità esplosiva dell'ordine di un megatone. (Gli effetti distruttivi di queste esplosioni sono discussi nel libro The effects of nuclear weapons pubblicato nel 1962 dal Dipartimento di Stato americano e dalla United States Atomic Energy Commission).

Il problema di come utilizzare una reazione di fusione per generare potenza controllata che possa essere convertita in energia elettrica o meccanica si è rivelato di difficilissima soluzione. Il problema cruciale consiste nel trovare il modo per contenere i nuclei di idrogeno della reazione a densità elevate, nonostante che la loro temperatura sia dell'ordine di 10⁸ OK. L'energia cinetica media dei nuclei deve quindi essere molte volte più grande dell'energia con cui legano a sé elettroni, di modo che nuclei ed elettroni si muovano indipendentemente gli uni dagli altri formando un gas di particelle cariche chiamato plasma. I tentativi fatti per costruire dei congegni atti a produrre potenza mediante fusione termonucleare sono stati diretti soprattutto alla ricerca del modo in cui contenere i nuclei e gli elettroni carichi in rapido movimento per mezzo di campi magnetici appositamente studiati. Finora, tuttavia, questi tentativi non hanno avuto successo, perché le particelle cariche in movimento creano esse stesse dei campi magnetici ed elettrici e sembrano sempre capaci di trovare un modo di muoversi tale che l'insieme dei campi magnetici propri e di quelli esterni permette loro di sfuggire dalla regione in cui dovrebbero rimanere imprigionati. L'incredibile varietà dei possibili modi secondo cui può muoversi un plasma caldo ha finora fatto fallire ogni tentativo di contenerlo per un tempo sufficiente e a una densità tale da permettere che avvenga un numero utile di reazioni di fusione. In venti anni di ricerche sono tuttavia stati fatti dei progressi notevoli in questa direzione e molti esperti prevedono che entro i prossimi dieci-trent'anni si troverà una soluzione attuabile. In vari laboratori si sta ora studiando un sistema alternativo per dare inizio a reazioni termonucleari controllate, consistente nell'illuminare una sferetta di idrogeno pesante solido con un fascio laser assai intenso. Quando si sarà riusciti a risolvere questo problema delle reazioni termonucleari controllate, si sarà risolto per sempre il problema del fabbisogno di energia dell'uomo.

Bibliografia.

Benedetti, S. de, Nuclear interactions, New York 1964.

Bohr, A., Mottelson, B., Nuclear structure, Amsterdam 1969.

Kopopinski, E. J., Theory of beta radioactivity, Oxford 1966.

Preston, M. A., Physics of the nucleus, Reading, Mass., 1962.

Segré, E., Nuclei and particles, Amsterdam 1964.

Reattori nucleari

SOMMARIO: 1. Introduzione. □ 2. Le leggi delle reazioni nucleari a catena: a) il processo di fissione; b) massa critica e reattività; c) materiale fissile e materiale fertile; d) moderatori e refrigeranti; e) classificazione dei reattori; f) sistemi di controllo, materiali, schermature. □ 3. I primi reattori nucleari: a) il Progetto Manhattan; b) l'‛incidente' del Gabon: un reattore nucleare naturale. □ 4. I reattori moderni: a) tipi di reattore; b) reattori ad acqua leggera; c) reattori ad acqua pesante e reattori a grafite; d) reattori autofertilizzanti; e) i reattori nucleari come parte del sistema energetico nucleare. □ 5. Previsioni e prospettive: a) consumi e fonti energetiche; b) l'umanità può convivere con la fissione? □ Bibliografia.

1. Introduzione.

Che nel nucleo vi fosse dell'energia potenzialmente utilizzabile era noto fin dalla scoperta della radioattività e delle sue connessioni con le trasmutazioni del nucleo atomico. Che questa energia fosse enorme, a paragone dell'energia chimica, divenne chiaro quando i fisici misurarono la variazione di massa nelle trasformazioni nucleari. L'energia liberata in una reazione tra due nuclei, secondo la relazione di Einstein E = mc² è generalmente dell'ordine del MeV (un milione di elettron-volt), mentre l'energia liberata quando due atomi si combinano per formare una molecola è appena di qualche eV.

Per molti anni, nonostante si fosse intuita la potenzialità dell'energia nucleare, nessuno fu in grado di immaginare un metodo adatto a liberare quest'energia su larga scala, tanto che ancora alla fine del 1933 lord E. Rutherford, fondatore della fisica nucleare, lo riteneva impossibile. Eppure, solo poche settimane più tardi, il fisico ungherese L. Szilard si rese conto che, se si fosse potuto trovare un processo nucleare innescato da un solo neutrone, che però desse luogo all'emissione di più di un neutrone e che fosse allo stesso tempo esoenergetico, cioè avvenisse con produzione di energia, allora sarebbe stato possibile ottenere energia attraverso una reazione nucleare su larga scala. Tale reazione prese il nome di ‛reazione a catena', poiché l'agente necessario per innescarla, cioè il neutrone, era prodotto dalla reazione stessa. Szilard fu il primo a concepire il modo in cui, in linea di principio, si sarebbe potuta ottenere liberazione di energia nucleare su larga scala. (Nel 1934 egli fece domanda per un brevetto che, più tardi, fu assegnato all'Ammiragliato britannico).

2. Le leggi delle reazioni nucleari a catena.

a) Il processo di fissione.

Al tempo in cui Szilard ebbe queste intuizioni non era noto alcun processo nucleare che soddisfacesse i requisiti della reazione a catena. Tuttavia nel 1938 O. Hahn e F. Strassmann scoprirono in Germania la fissione del nucleo di uranio: processo che rispondeva pienamente a tutti i requisiti posti da Szilard. Nella fissione dell'uranio (o di altri nuclidi fissionabili) inizialmente il nucleo assorbe un neutrone. L'energia che viene così ceduta al nucleo, corrispondente all'energia cinetica del neutrone e alla sua energia di legame, è pari a circa 6 MeV. Questa energia supplementare può deformare il nucleo, inizialmente di forma sferoidale, e alla fine provocarne la rottura, cioè fissionarlo in frammenti circa eguali tra loro, detti prodotti di fissione.

L'energia totale rilasciata in ogni processo di fissione è dell'ordine di 200 MeV. Per avere un termine approssimativo di raffronto, si può calcolare che la fissione di 1 grammo di uranio produca circa 1 MW-giorno di energia: per produrre la stessa quantità di energia occorrerebbero circa 4 tonnellate di carbone. Dei 200 MeV liberati nella fissione circa 168 MeV sono ceduti come energia cinetica ai frammenti della fissione. In materiali densi questi frammenti vengono fermati dopo aver percorso brevi distanze, dell'ordine di qualche micron, e la loro energia viene convertita in calore. La maggior parte del calore prodotto in un reattore nucleare o in una bomba atomica proviene dalla dissipazione dell'energia cinetica dei prodotti di fissione formatisi nella rottura del nucleo.

La maggior parte dell'energia restante è liberata durante la fissione sotto forma di energia di eccitazione dei frammenti e si manifesta come radiazione γ. Poiché i nuclidi pesanti hanno un numero di neutroni superiore a quello relativo ai prodotti di fissione, questi ultimi, essendo troppo pesanti in rapporto alla loro carica, subiscono generalmente un decadimento β che ne aumenta il numero atomico. Questa radiazione, di energia pari a circa 14 MeV per fissione (di cui circa 6 MeV come raggi γ e 8 MeV come raggi β), è liberata gradualmente. Così circa il 7% dell'energia prodotta da un reattore nucleare è liberato come ‛calore ritardato', cioè come energia dovuta al decadimento radioattivo dei prodotti di fissione.

A causa di questo eccesso di neutroni, durante la fissione sono emessi generalmente due o tre neutroni. Questi neutroni di fissione presentano un ampio spettro di energie, il cui valor medio è di circa 2 MeV; tale valore va confrontato con quello dell'energia dei neutroni che inducono la fissione, che può essere anche di solo 1/40 di eV, se i neutroni sono in equilibrio termico con il mezzo circostante.

b) Massa critica e reattività.

I neutroni, privi come sono di carica elettrica, possono percorrere (o ‛migrare' per) distanze macroscopiche (centimetri o più) perfino in materiali densi come l'acqua o la grafite, prima di essere definitivamente catturati. Nel loro vagare i neutroni urtano contro i nuclei del ‛moderatore' e, proprio come una palla da biliardo che, quando urta contro un'altra palla ferma, perde un po' della propria energia, essi perdono la loro energia, cioè vengono ‛moderati'. Alla fine il neutrone viene ‛termalizzato', cioè raggiunge l'equilibrio con gli atomi del moderatore che effettuano movimenti termici casuali. Neutroni di questo tipo sono detti neutroni ‛lenti' o ‛termici', mentre i neutroni di energia più elevata sono detti ‛veloci'.

Poiché i neutroni migrano abbastanza liberamente, essi possono sfuggire da un moderatore di limitate dimensioni. Questo fatto ci conduce immediatamente al concetto di ‛massa critica': non si avrà alcuna reazione a catena se la quantità di materiale fissile è troppo piccola, poiché troppi neutroni sfuggiranno prima di provocare la fissione. Se si aumenta la massa, il rapporto superficie-volume decresce e lo stesso accade per la frazione di neutroni che sfuggono all'esterno. Quindi aumentando la massa si può raggiungere uno stadio nel quale la produzione e la perdita di neutroni si equilibrano. Il reattore è allora ‛critico' e la reazione a catena si può sostenere.

I reattori vengono perciò caratterizzati dal loro fattore di criticità k = neutroni prodotti al secondo/neutroni rimossi al secondo.

Nel denominatore sono compresi i neutroni che si perdono attraverso tutti i possibili meccanismi: i neutroni utilizzati per produrre la fissione, quelli assorbiti senza causare la fissione e i neutroni che sfuggono all'esterno. Se k = 1 la reazione a catena è ‛critica' e può essere mantenuta stabilmente a qualsiasi intensità. Se k 〈 1 la reazione è ‛supercritica' e cresce esponenzialmente, come accade nella bomba atomica; se k > 1 la reazione è ‛sottocritica' e si spegne, a meno che non sia alimentata da una sorgente esterna di neutroni.

La quantità k - 1 è chiamata ‛reattività' del reattore.

c) Materiale fissile e materiale fertile.

I nuclidi ‛fissili' sono quelli che subiscono la fissione con neutroni di qualsiasi energia: essi sono, in genere, isotopi degli elementi più pesanti con numero dispari di neutroni, vale a dire hanno numero atomico pari e numero di massa dispari. I nuclidi fissili più importanti sono i seguenti: ²³³U, ²³⁵U, ²³⁹Pu e ²⁴¹Pu. Tutti questi nuclidi sono instabili e decadono con emissione di particelle α, attraverso processi che, tuttavia, richiedono migliaia o milioni di anni. Sebbene l'assorbimento di un neutrone da parte di un nuclide fissile produca generalmente la fissione, talvolta il nuclide cattura semplicemente il neutrone senza che avvenga la fissione. Il rapporto tra la probabilità di cattura senza fissione e la probabilità di fissione (indicato comunemente con α) dipende dal nuclide e dall'energia del neutrone incidente ed è minore per i neutroni veloci che per quelli lenti. Poiché la cattura senza fissione porta semplicemente alla perdita di un neutrone, il numero medio di neutroni prodotti per neutrone assorbito (indicato con η) tende ad aumentare al crescere dell'energia del neutrone incidente.

Nella tab. I sono dati i valori di α, η e della sezione d'urto σ_f (che è essenzialmente la probabilità che un nuclide subisca la fissione quando è sottoposto al bombardamento di un fascio di neutroni) per tre diverse energie: termica, cioè di 0,025 eV, di 200 keV, tipica dei reattori veloci, e di I MeV.

Dei nuclidi fissili solo l'²³⁵U si trova in natura sulla Terra: esso rappresenta lo 0,72% dell'uranio naturale, che è costituito essenzialmente da ²³⁸U. Perciò, se si irraggia una massa di uranio naturale con neutroni, la maggior parte di essi saranno catturati dall'²³⁸U senza causare la fissione. È molto più facile, pertanto, ottenere la reazione a catena nell'uranio arricchito dell'isotopo ²³⁵U che nell'uranio naturale. Tale arricchimento richiede processi di separazione isotopica molto complessi e costosi.

Gli altri nuclidi fissili possono essere prodotti mediante l'assorbimento di neutroni in nuclidi ‛fertili': ²³²Th, ²³⁸U, ²⁴⁰Pu, che, dopo un decadimento β intermedio, danno luogo, rispettivamente, a ²³³U, ²³⁹Pu e ²⁴¹Pu. In realtà fu il ²³⁹Pu il primo nuclide fissile a essere prodotto in quantità macroscopiche, senza ricorrere alla separazione isotopica. Anche gli isotopi fertili subiscono la fissione da parte di neutroni di elevata energia (???54??? 0,5 MeV); gli isotopi fertili, tuttavia, non sono in grado di sostenere da soli una reazione a catena, poiché i neutroni vengono rapidamente rallentati fino a energie inferiori a quella alla quale sono in grado di provocare la fissione.

d) Moderatori e refrigeranti.

Poiché le sezioni d'urto di fissione dei nuclidi fissili sono molto più elevate per i neutroni termici che per quelli veloci (v. tab. I), occorre meno materiale fissile per ottenere una reazione a catena basata su neutroni termici di quanto ne occorra se si utilizzano neutroni veloci. Pertanto in molti reattori il materiale fissile è immerso in un ‛moderatore' che rallenta i neutroni emessi nella fissione. Il moderatore si può scegliere tra quegli elementi leggeri che assorbono poco i neutroni, come l'idrogeno, il deuterio, il berillio, il carbonio e l'ossigeno; generalmente si fa uso di un composto chimico, come, per es., H₂O, D₂O, ZrH, BeO, che contenga l'elemento moderatore. I moderatori vengono caratterizzati dalla loro ‛distanza di rallentamento', vale a dire dalla distanza media che un neutrone deve percorrere, a partire dalla sua nascita come neutrone veloce, prima di mettersi in equilibrio termico con gli atomi del moderatore. Le dimensioni dell'insieme in cui avviene la reazione a catena cioè la sua dimensione critica, sono in larga misura determinate dalla distanza di rallentamento del moderatore. I reattori moderati ad H₂0 sono in genere assai più compatti di quelli moderati à grafite (carbonio), poiché la distanza di rallentamento dell'H₂0 è circa un terzo di quella della grafite.

A qualsiasi potenza (purché non minima) si faccia lavorare un reattore, occorre estrarre da esso il calore prodotto e ciò richiede la circolazione di un refrigerante in forma liquida o gassosa. Come il moderatore, anche il refrigerante dev'essere un debole assorbitore di neutroni. Tra gli altri sono stati usati come refrigeranti nei reattori H₂, H₂O, D₂O, He, Co₂, Na e perfino il combustibile stesso in soluzione acquosa oppure come sale fuso.

e) Classificazione dei reattori.

I reattori nucleari possono essere costruiti secondo varie configurazioni strutturali e geometriche. Tali configurazioni possono essere eterogenee, e in questo caso il materiale fissile è disposto in elementi di combustibile cilindrici o piani separati tra loro dal moderatore e dal refrigerante; oppure il combustibile può essere disperso più o meno omogeneamente nel moderatore o perfino disciolto in esso. In genere gli elementi di combustibile debbono essere inseriti in incamiciature e sostenuti per far fronte agli sforzi termici e meccanici. Anche in questo caso i materiali che possono essere utilizzati per le strutture o le incamiciature debbono presentare un assorbimento neutronico relativamente basso: grafite, alluminio, zirconio, magnesio o acciaio. Il reattore stesso è usualmente composto da un ‛nocciolo' o ‛reticolo attivo' contenente il materiale fissile e da un riflettore che circonda il nocciolo e restituisce una parte di neutroni che altrimenti sfuggirebbe all'esterno. Se il riflettore contiene materiale fertile, ed è così sede di produzione di nuovo materiale fissile, viene chiamato in genere ‛mantello' o ‛mantello fertilizzante'.

Non tutte le combinazioni di strutture o di materiali sono realizzabili; rimangono, tuttavia, in ogni caso molte scelte possibili, alcune delle quali saranno descritte più avanti. La classificazione più importante dei reattori è quella che si esegue tenendo conto dell'energia dei neutroni. Se i neutroni sono moderati, allora si parla di ‛reattori termici. Tali reattori richiedono, in genere, una disposizione omogenea, in modo che non vengano assorbiti troppi neutroni nei processi di rallentamento. Poiché i reattori termici, in genere, non sono arricchiti completamente, essi contengono anche materiali fertili, per esempio l'²³⁸U, che, per assorbimento neutronico, viene convertito in ²³⁹Pu, fissile. Tali reattori termici sono chiamati anche ‛convertitori'. Il rapporto di conversione è definito come il numero di nuclei di nuovi isotopi fissili prodotti per ogni nucleo di isotopo fissile distrutto per fissione o per cattura. Questa conversione, in una certa misura, permette una migliore utilizzazione del combustibile. Così, sebbene l'¹¹⁵U sia presente nell'uranio naturale nella concentrazione di appena lo 0,72%, riciclando il ²³⁹Pu prodotto nella reazione si può accrescere lo sfruttamento dell'uranio in un reattore termico fino a circa l'1 o l'1,5%.

All'altro estremo si collocano i reattori che contengono pochi (o non contengono affatto) materiali moderatori e che quindi hanno un'alta concentrazione di isotopi fissili. Essi sono chiamati ‛reattori veloci', poiché i neutroni, non essendo moderati, non raggiungono l'energia termica. In ogni caso i neutroni perdono energia in collisioni anelastiche, così che la loro energia media è considerevolmente più bassa di quella dei neutroni appena generati. Poiché il numero di neutroni per fissione è maggiore di 2 e aumenta con l'energia dei neutroni e poiché a (v. tab. I) decresce alle alte energie, è relativamente facile ottenere in un reattore veloce un rapporto di conversione maggiore di 1 , cioè una situazione nella quale si producono più nuclidi fissili di quanti non se ne distruggano. Si parla allora di ‛autofertilizzanti' e di ‛rapporto di fertilizzazione'. Il processo di autofertilizzazione dischiude la possibilità di utilizzare tutto l'uranio o il tono disponibili, invece della piccola frazione del raro ²³⁵U, oltre alla piccola quantità di ²³⁹Pu ottenuta per conversione. In linea di principio la fertilizzazione è possibile sia nel sistema ²³⁸U-²³⁹Pu, che opera con neutroni veloci, sia nel sistema ²³²Th-²³³U, che utilizza neutroni veloci o termici, sebbene il rapporto teorico di fertilizzazione nel primo caso sia considerevolmente più alto che nel secondo (v. tab. I).

f) Sistemi di controllo, materiali, schermature.

In condizioni stazionarie il fattore di criticità k dev'essere mantenuto eguale a 1. Inoltre il reattore deve poter essere avviato o spento a comando e pertanto dev'essere dotato di mezzi di controllo. La natura in questo è stata generosa, perché ha fornito un margine di sicurezza sotto forma di un ritardo, variabile da alcuni secondi a un minuto circa, con cui viene emessa una piccola frazione (inferiore all'1% e dipendente dal tipo di materiale fissile) di neutroni. Questo ritardo è dovuto al fatto che tali neutroni sono emessi dai prodotti della fissione dopo che questi hanno subito uno o più decadimenti radioattivi. Ciò fa sì che la scala temporale di un reattore prossimo alla criticita sia determinata dai neutroni ritardati e non dai brevi intervalli fra fissioni successive; comunque, se k supera 1 di una quantità maggiore della frazione dei neutroni ritardati, la reazione a catena può essere mantenuta dai soli neutroni pronti. La reazione, in questo caso, divergerà molto rapidamente; questa è la situazione che si presenta nel caso della bomba atomica, ma che dev'essere rigorosamente evitata in reattori che operino in condizioni stazionarie. I mezzi di controllo che di fatto si utilizzano consistono in genere in materiali a forte assorbimento neutronico, come il ¹⁰B, contenuto in barre di controllo che possono essere inserite o estratte dal reattore. È necessario sia poter compensare piccole variazioni nella reattività, mediante un sistema di controllo fine, sia poter spegnere rapidamente il reattore in ogni circostanza ipotizzabile, mediante il cosiddetto ‛sistema di scram'. Nei reattori attuali vi sono in genere molte barre, ciascuna con propria strumentazione e sistema di guida, e un sistema ausiliario per permettere una rapida e consistente riduzione di reattività.

Un altro fattore che contribuisce al controllo del reattore è un coefficiente negativo di reattività termica, cioè un fattore di criticità che cala al crescere della temperatura e che fa sì che la reazione a catena diminuisca concordemente. La maggior parte dei reattori hanno (o si può far sì che abbiano) questa proprietà di autoregolazione.

Occorre grande cura nella scelta e nel trattamento dei materiali da usare in un reattore. Bisogna purificarli dai contaminanti che assorbono neutroni; ma, soprattutto, si devono tenere presenti le condizioni di lavoro molto severe cui sono sottoposti: alta temperatura, sforzi termici e meccanici e radiazione molto intensa. Le collisioni con i neutroni e con i prodotti di fissione energetici producono dislocazioni in qualsiasi solido e provocano la decomposizione dei composti chimici. Accade, infatti, che ogni atomo nel nocciolo di un reattore di potenza subisca molteplici spostamenti nel corso della vita del reattore. In conseguenza di ciò i metalli nel nocciolo del reattore possono gonfiarsi e diventare più fragili. Talvolta piccole variazioni nel processo di fabbricazione possono produrre comportamenti assai diversi dei materiali sottoposti a irraggiamento. Lo stesso combustibile, in genere un ossido di uranio, si deforma e si fessura, in larga parte perché alcuni dei prodotti di fissione sono gas (kripton e xenon) che debbono trovar posto nel reticolo cristallino del combustibile.

Poiché un reattore produce neutroni, raggi gamma, prodotti di fissione e isotopi pesanti altamente radioattivi, esso dev'essere schermato in modo da ridurre la dose di radiazione esterna a un livello di sicurezza. Alcuni dei prodotti di fissione sono molto mobili: il combustibile è perciò solitamente rivestito di materiali a bassa permeabilità e occorre esercitare un attento controllo di tutti gli effiuenti liquidi e gassosi. Poiché la vita degli elementi del combustibile è in genere la più breve tra quelle di tutti i componenti, si è posta particolare cura nel progetto di meccanismi per il carico del combustibile fresco e per lo scarico degli elementi di combustibile spento (altamente radioattivi).

Di fronte a tanti requisiti da soddisfare, che in parte sono in contraddizione tra di loro, il progettista di un reattore deve considerare il reattore, assieme alle sue attrezzature ausiliarie quali le pompe, la strumentazione, le valvole, gli scambiatori di calore ecc., come un unico sistema e studiario come tale. Lo stesso approccio dev'essere usato anche nella progettazione del ciclo del combustibile, per definire la natura degli elementi del combustibile, le loro caratteristiche costruttive e di burnup, lo schema di ricaricamento e il riprocessamento finale. Quest'ultimo processo includerà la separazione dei rifiuti dai materiali fertili e fissili ancora utilizzabili, l'eliminazione dei primi e il riprocessamento degli ultimi. Il ciclo del combustibile è, a parte il costo iniziale del materiale grezzo, il fattore più importante nell'economia dei reattori di potenza.

3. I primi reattori nucleari.

a) Il Progetto Manhattan.

La scoperta della fissione e l'inizio della seconda guerra mondiale innescarono negli Stati Uniti il grandioso Progetto Manhattan. Nei laboratori di Chicago, Oak Ridge, Los Alamos e altrove si gettarono le fondamenta di quasi tutti i settori della tecnologia dei reattori. In un certo senso si trattò di una collaborazione a livello internazionale. Importanti contributi furono forniti dal Regno Unito e dal Canada e molte delle personalità chiave, come E. Fermi, L. Szilard e E. Wigner erano di origine europea. Anche dalla Francia pervennero contributi sostanziali, da parte di Fr. Joliot-Curie, H. von Halban e altri, ma tutti i contatti furono interrotti dopo l'occupazione tedesca. (La Germania organizzò il proprio Progetto Uranio sotto la direzione di W. K. Heisenberg e W. W. Bothe. I tedeschi si proponevano di usare come moderatore l'acqua pesante, ma alla fine della guerra erano ancora assai lontani dall'aver raggiunto la criticità, né compresero mai fino in fondo la possibilità di utilizzare il plutonio. I russi ottennero la loro prima reazione a catena nel 1947, sotto la guida di I. V. Kurčatov).

Fin dall'inizio del 1942 gli scienziati sapevano che la componente fissile dell'uranio era l'isotopo raro ²³⁵U, che emetteva più di 2 neutroni per fissione, e che la cattura neutronica da parte dell'²³⁸U avrebbe prodotto il ²³⁹Pu. Se si fosse prodotto abbastanza ²³⁹Pu, si sarebbe potuto utilizzarlo come materiale per una bomba a fissione, senza bisogno di effettuare la separazione isotopica, necessaria in caso di impiego dell'²³⁵U.

L'impulso alla costruzione di un reattore divenne allora formidabile e un gruppo diretto da Fermi, allora a Chicago, si accinse all'impresa. La prima scelta critica fu quella del moderatore. L'idrogeno è un fortissimo assorbitore di neutroni, cosicché non è possibile ottenere una reazione a catena con uranio naturale e acqua. L'acqua pesante (D₂O) è un moderatore ideale, ma a quell'epoca non era disponibile in quantità sufficienti, cosicché la scelta cadde sul carbonio, sotto forma di grafite.

Il fattore di criticità di un insieme di materiale fissile può essere misurato mediante il cosiddetto esperimento esponenziale, anche se l'insieme è sottocritico (k > 1), o perché ha dimensioni troppo piccole o perché non ha sufficiente reattività intrinseca. Questo esperimento consiste essenzialmente nella misura della moltiplicazione dei neutroni provenienti da una sorgente esterna: la moltiplicazione è dell'ordine di 1/(1 − k) ed è pertanto molto grande se k è vicino all'unità. Si eseguirono molti esperimenti del genere per determinare le migliori proprietà geometriche e nucleari dei materiali da usare nell'insieme; si trovò che l'uranio e la grafite che si avevano a disposizione contenevano troppe impurezze che assorbivano neutroni e si intraprese quindi un esteso programma di purificazione. Alla fine si ebbe a disposizione materiale puro a sufficienza e il 2 dicembre 1942 a Chicago fu ottenuta la prima reazione a catena artificiale.

Il reattore, o pila, come fu chiamato, consisteva di un reticolo di blocchi, in parte di uranio metallico e in parte di ossido di uranio, UO₂, ognuno contenente circa 2 kg di uranio. La cella del reticolo era cubica, col lato di 23 cm e l'intera pila era approssimativamente sferoidale con un raggio medio pari a circa 355 cm. Il reattore conteneva 6 t di uranio metallico, 34 t di ossido di uranio e 385 t di grafite. La massima potenza, erogabile solo per brevi intervalli, era di circa 200 W. Dato questo basso livello di potenza non fu necessario nè schermare nè raffreddare. Il reattore veniva controllato con barre azionate a mano.

Il successo di questo esperimento piuttosto primitivo e la pressione degli eventi bellici portarono in un tempo eccezionalmente breve alla costruzione di una famiglia di discendenti della pila di Fermi, di dimensioni molto più grandi, anch'essi moderati a grafite. Quello costruito a Oak Ridge nel Tennessee fu il primo a produrre quantità significative di calore; era munito di schermature in cemento e di un sistema di raffreddamento ad aria e divenne critico nel dicembre 1943. Questo reattore a grafite usava dischi di uranio metallico rivestiti di alluminio e disposti secondo la configurazione di un reticolo a barre: generava fino a 3 MW termici e produsse anche alcuni chilogrammi di plutonio. Infine i reattori di Hanford, progettati da Wigner e dai suoi colleghi, erano raffreddati ad acqua. Questi reattori funzionarono senza incidenti alla potenza di 250 MW e ciascuno produsse 250 g di Pu al giorno a partire dalla fine del 1944, appena due anni dopo che Fermi aveva realizzato la prima reazione a catena prodotta dall'uomo.

Discendenti più lontani del reattore a uranio naturale e moderato a grafite furono i primi reattori di potenza inglesi, del tipo di quello di Calder Hall, e i reattori francesi di Marcoule, gli uni e gli altri raffreddati a CO₂. Lo sviluppo più avanzato del reattore del tipo Hanford è costituito forse dall'ultimo reattore Hanford-N, nel quale l'acqua è messa in pressione per poter raggiungere temperature sufficienti per la produzione di vapore, e quindi di elettricità, e nel quale si produce anche plutonio. Il reattore eroga una potenza di 4.000 MW termici e 800 MW elettrici. Un reattore simile, moderato a grafite e raffreddato ad acqua, è stato realizzato anche in URSS.

Oltre che dei reattori a grafite, il Progetto Manhattan si occupò anche di altri tipi di reattori. L'acqua pesante fu usata per la prima volta, sia come moderatore sia come refrigerante, da W. Zinn, presso l'Argonne National Laboratory vicino a Chicago, nella serie di reattori CP. Le eccellenti proprietà nucleari del D₂O permettono un po' più di libertà nella progettazione del reattore. Di questa circostanza si avvalsero gli Stati Uniti, per i reattori plutonigeni di Savannah River, e il Canada, dove, sotto la direzione di W. Bennett Lewis, fu costruita una serie di pregevoli reattori di ricerca e infine la serie dei reattori di potenza CANDU. Tutti questi reattori funzionano con uranio naturale o arricchito molto debolmente.

Al laboratorio militare di Los Alamos l'uso nei reattori di uranio arricchito in ²³⁵U costituì uno sviluppo naturale. Il primo reattore ivi costruito fu la ‛caldaia ad acqua', una soluzione acquosa di nitrato di uranile arricchito in un recipiente di acciaio inossidabile. Questo è il reattore più semplice possibile che ha la più piccola massa critica, meno di 1 kg di uranio altamente arricchito, e può essere considerato il predecessore di vari modelli in cui il combustibile, in forma liquida, viene fatto circolare attraverso uno scambiatore interno di calore, evitando così di predisporre un circuito di refrigerazione separato. L'esperimento della caldaia ad acqua dimostrò che quantità relativamente modeste di uranio arricchito o di plutonio in presenza di acqua possono diventare critiche; ciò impone severe limitazioni all'uso e al trattamento di tali materiali se si vogliono evitare incidenti di criticità.

Una concezione che ha poi esercitato una notevole in- fluenza fu quella del reattore ad alto flusso progettato ad Oak Ridge nel 1946 e costruito come reattore di prova materiali o MTR (da Materials Testing Reactor) a Idaho Falls nel 1952. Era costituito da insiemi di sottili lastre di uranio arricchito, rivestite di alluminio, attraverso le quali veniva fatta circolare a grande velocità acqua leggera, che fungeva sia da moderatore che da refrigerante. La configurazione compatta e la refrigerazione efficiente così ottenute permisero di aumentare notevolmente la densità di potenza: l'MTR ha operato per 20 anni a 40.000 kW e con una densità media di potenza pari a 400 kW/litro. L'MTR è pertanto un predecessore del reattore ad acqua leggera (Light Water Reactor, LWR) che è ora utilizzato nella propulsione navale e in molte moderne centrali di potenza.

Il lavoro di Los Alamos, per le sue stesse caratteristiche, richiese esperimenti di criticità su materiali a forte tenore di ²³⁵U e di ²³⁹Pu. Perciò fu relativamente breve il passo fatto per concepire reattori simili che funzionassero in modo continuo con neutroni veloci, non moderati. A parte insiemi non refrigerati, che talvolta venivano fatti funzionare in modo pulsato, il primo effettivo reattore veloce fu ‛Clementine' (1946). Caricato con plutonio e refrigerato con mercurio, erogava una potenza di 10 kW e dimostrò che un reattore veloce di quel tipo funzionava bene e in modo sicuro. I successivi reattori veloci furono i due Experimental Breeder Reactors, EBR I e Il, progettati all'Argonne National Laboratory e costruiti a Idaho Falls nel 1951 e nel 1954. L'EBR I e l'EBR Il, a uranio arricchito, erano raffreddati con sodio liquido: essi dimostrarono con successo il principio della fertilizzazione e possono essere considerati i veri predecessori dei moderni reattori veloci autofertilizzanti a metallo liquido.

b) L'‛incidente' del Gabon: un reattore nucleare naturale.

Fino al 1972 si riteneva che la reazione a catena creata da Fermi nel 1942 fosse un fenomeno nuovo e unico. Nel 1972 scienziati francesi del Commissariat à l'Énergie Atomique annunciarono di aver scoperto un reattore naturale vicino a Oklo, nel Gabon, che aveva funzionato circa 1.800 milioni di anni orsono. In quell'epoca, poichè l'²³⁵U decade 6 volte più rapidamente dell'²³⁸U, il rapporto ²³⁵U/²²⁸U era eguale a 3,5% invece che a 0,72%.

Con una concentrazione di ²³⁵U così alta si può mantenere una reazione a catena con l'acqua ordinaria come moderatore. Verosimilmente in questi depositi molto ricchi di uranite, una volta saturati di acqua piovana, si accese in modo intermittente una reazione a catena per circa un milione di anni, finchè l'²³⁵U diminuì in misura tale che la reazione a catena non fu più possibile. L'energia totale generata dai reattori nucleari naturali di Oklo dovette essere dell'ordine di 10.000 MW-anno: durante il periodo di funzionamento si formarono più di una tonnellata di ²³⁹Pu e circa quattro tonnellate di prodotti di fissione fortemente radioattivi. Da allora tutta questa radioattività è decaduta e il plutonio, con un tempo di dimezzamento di 24.000 anni, si è tramutato in ²³⁵U. Forse l'aspetto più importante dei reattori di Oklo è che molti prodotti di fissione e più dell'80% del ²³⁹Pu sono rimasti sul posto. Sembra così che, in questo caso, la Terra abbia dimostrato la propria capacità di trattenere la maggior parte dei rifiuti radioattivi creati da un reattore nucleare.

4. I reattori moderni.

a) Tipi di reattore.

Come abbiamo visto, i reattori nucleari si possono costruire con materiali fissili, moderatori refrigeranti, materiali fertili, spettri energetici di neutroni e configurazioni del materiale fissile di diversi tipi. Nei primi 20 anni dello sviluppo dei reattori nucleari di potenza sono stati studiati in modo approfondito circa due dozzine di sistemi diversi. Oggi, tuttavia, i reattori di potenza si limitano a pochi tipi fondamentali, che abbiamo indicato, assieme ad alcuni tipi promettenti in fase sperimentale, nella tab. Il.

b) Reattori ad acqua leggera.

Mentre i primi reattori funzionavano a livelli di potenza modesti, da 50 a 100 megawatt elettrici (MWe), le economie di scala hanno indotto a realizzare dimensioni sempre maggiori. La generazione attuale lavora su unità con potenze da 500 a 1.300 MWe e già si prospetta l'introduzione di unità ancora più grandi. Il reattore più diffuso nel mondo è quello ad acqua leggera debolmente arricchito (LWR), ampiamente utilizzato in due versioni. Nel reattore ad acqua pressurizzata (PWR; v. fig. 1) il calore viene trasferito dagli elementi di combustibile a uno scambiatore di calore intermedio, dove si genera il vapore; il vapore aziona un turbogeneratore convenzionale che produce elettricità. Nel reattore ad acqua bollente (BWR) si porta l'acqua a ebollizione nel reattore e la si manda direttamente dal reattore al turbogeneratore.

Un tipico reattore BWR da 1.000 MWe è illustrato nella fig. 2. Il combustibile è formato da pastiglie di ossido di uranio arricchito al 2-3%, del diametro di circa 1 cm. Queste pastiglie sono contenute in tubi di lega di zirconio lunghi 400 cm. Circa 64 di queste barre di combustibile formano un elemento di combustibile e il nocciolo del reattore consiste di circa 700 elementi di combustibile inseriti in modo compatto in un grande recipiente a pressione. Barre di controllo cruciformi, che assorbono i neutroni, entrano nel reticolo attivo dal di sotto. L'acqua entra nel reticolo dal basso ed esce dall'alto sotto forma di miscela di acqua e vapore a circa 70 atmosfere e 280 °C. Le goccioline d'acqua vengono rimosse nei separatori di vapore e negli essiccatori posti sopra il reticolo attivo e il vapore secco viene trasferito al turbogeneratore. Dopo che il vapore si è espanso attraverso l'ultimo stadio a bassa pressione della turbina a vapore, viene condensato e restituito al reattore dalle pompe di alimentazione dell'acqua ad alta pressione.

I reattori ad acqua leggera all'inizio furono concepiti non come centrali di potenza commerciali ma piuttosto come impianti per navi nucleari. Per questo tipo di applicazione la prerogativa principale era la compattezza e non l'economia. E sorprendente il fatto che un reattore proposto all'origine per la sua compattezza (che è connessa direttamente al piccolo cammino libero medio dei neutroni in acqua) sia, a quanto sembra, divenuto il più diffuso tra i reattori nucleari di potenza per i quali le esigenze principali sono la sicurezza e il basso costo complessivo, e non la compattezza.

Le ragioni di questa preferenza possono essere spiegate sulla base dei punti seguenti: 1 ) il grande successo degli impianti di diffusione gassosa per la separazione degli isotopi dell'uranio ha mantenuto i costi dell'uranio arricchito, usato negli LWR, entro limiti accettabili; 2) la compattezza degli LWR contribuisce a tenere basso il loro costo. Con la produzione di grandi recipienti a pressione, del peso di circa 1.000 tonnellate, sono diventati fattibili reattori capaci di produrre più di 1.000 MWe. Così i moderni LWR permettono di realizzare vantaggiose economie di scala ; 3) lo sviluppo dei reattori navali ha dato un grande impulso e un vantaggio iniziale alla tecnologia degli LWR. Altri tipi di reattori hanno incontrato difficoltà a recuperare lo svantaggio.

D'altra parte la compattezza degli LWR comporta anche alcuni inconvenienti. Questi reattori hanno bisogno di sistemi complessi per la refrigerazione di emergenza del nocciolo (o ECCS, da Emergency Core Cooling Systems), atti a impedire la fusione in caso di guasto del normale sistema di refrigerazione. Così il reattore LWR, concettualmente semplice, nel quale l'H₂O funge sia da refrigerante che da moderatore, è in concreto un sistema meccanico molto complicato.

c) Reattori ad acqua pesante e reattori a grafite.

I sistemi competitivi con gli LWR usano come moderatore l'acqua pesante o la grafite. I reattori a D₂O, o HWR, da Heavy Water Reactors, possono essere alimentati con uranio naturale, il che rende meno costoso il loro ciclo del combustibile. Questi reattori sono stati realizzati essenzialmente nel Canada, in Francia e nel Regno Unito, ma nessuno di questi paesi aveva impianti di separazione di dimensioni paragonabili a quelle degli impianti americani o sovietici. Gli elementi di combustibile sono molto simili a quelli degli LWR. I fasci di elementi sono però molto distanziati tra di loro dal moderatore, così che questi sistemi sono molto meno compatti degli LWR. Ciò rende non conveniente l'uso di un recipiente a pressione per l'intero reattore. Ogni fascio di elementi di combustibile, invece, è incapsulato in un tubo in pressione separato dagli altri, nel quale si fa circolare come refrigerante H₂O o D₂O. Il sistema generale di raffreddamento è perciò abbastanza complesso. Gli ECCS possono invece essere un po' più semplici di quelli degli LWR. Vi sono attualmente in regolare funzionamento vari reattori ad acqua pesante, il più grande dei quali (costruito nel 1975 a Pickering nel Canada) è costituito da 4 unità da 500 MWe ciascuna.

Il sistema più moderno basato sulla grafite è quello del reattore ad alta temperatura raffreddato a gas (HTGR; v. fig. 3), sul quale si è lavorato soprattutto negli Stati Uniti, in Germania e nel Regno Unito. L'innovazione principale consiste nel fatto che il combustibile non è contenuto in elementi inseriti dentro incamiciature di metallo, ma in particelle ‛rivestite', formate da un piccolo nocciolo di materiale fissile o fertile, consistente in ossidi o carburi, circondato da strati di grafite pirolitica densa e impermeabile; tali particelle possono anche includere un sottilissimo strato di carburo di silicio. Il diametro delle particelle rivestite è dell'ordine di alcune centinaia di micron. Le particelle formano, con un legante in grafite, delle bacchette disposte in blocchi prismatici di grafite che contengono condotti per la circolazione del refrigerante. L'uso dell'elio come refrigerante, assieme alla proprietà della grafite, permette di operare ad alte temperature, fino a 1.000 °C e più. Il ciclo del combustibile più vantaggioso si realizza con l'uso dell'²³⁵U oppure dell'²³³U fortemente arricchito come materiale fissile, e del ²³²Th come materiale fertile. I vantaggi dell'HTGR sono: il funzionamento ad alte temperature, che implica un'elevata efficienza termodinamica, una buona economia neutronica, aspetto questo condiviso anche dall'HWR, e sicurezza di esercizio, dovuta all'impossibilità di una fusione e all'elevata capacità termica dell'intero reattore. Un prototipo di HTGR è stato costruito a Fort St. Vrain nel Colorado.

Riassumendo, sembra probabile che il reattore LWR, attualmente in posizione dominante, manterrà un vantaggio nel costo iniziale per kW di elettricità generata. Questo vantaggio è annullato, nei reattori a D₂O, dai minori costi del ciclo del combustibile, in quanto questi reattori possono impiegare uranio naturale, e, nei reattori del tipo HTGR, dall'efficienza neutronica e termodinamica, dalla versatilità e dalla possibilità di utilizzare, come materiale fertile, il tono, abbondante e potenzialmente a buon prezzo. Ambedue queste alternative sembrano vantaggiose anche dal punto di vista della sicurezza. C'è dunque da attendersi che nel prossimo decennio vi sarà una forte concorrenza tra questi tre tipi fondamentali di reattori: la scelta dell'uno piuttosto che dell'altro dipenderà sia da considerazioni politiche e locali sia da valutazioni di tipo strettamente economico.

d) Reattori autofertilizzanti.

I reattori del tipo descritto nel paragrafo precedente, LWR, HWR, HTGR, sono tutti convertitori che lavorano con neutroni termici e che utilizzano l'uranio con scarsa efficienza con rapporti di conversione inferiori a 1. Come è stato messo in evidenza (v. sopra, cap. 2, È e) si può elevare al disopra di 1 il valore del rapporto di conversione e così ottenere la fertilizzazione dei materiali fissili e utilizzare tutte le risorse di uranio e torio. Ciò può essere fatto sia con reattori veloci che con reattori termici basati sul ciclo ²³³U-²³²Th.

I reattori autofertilizzanti sono ancora in una fase attiva di sviluppo. La linea principale su cui si lavora è rappresentata dal Liquid Metal Fast Breeder Reactor (LMFBR). Nella configurazione prevista attualmente, un LMFBR consiste di un reticolo compatto di barre di combustibile, analogo al nocciolo di un LWR. Il combustibile consiste di pastiglie di ossidi misti PuO₂ (dal 10 al 15%) e UO₂, contenute in tubi di acciaio inossidabile. Nell'insieme un LMFBR da 100 MWe può contenere 3 t di plutonio. Attorno al nocciolo attivo vi è un mantello fertilizzante costituito da UO₂ naturale o addirittura impoverito: il plutonio si crea sia nel mantello che nel nocciolo. L'intero sistema è immerso in un flusso di sodio liquido che porta il calore dal reattore a uno scambiatore di calore intermedio. Qui il calore viene trasferito al refrigerante secondario (ancora sodio), che produce infine vapore in un generatore di vapore. Il circuito secondario del sodio si usa in quanto il sodio del primario diventa fortemente radioattivo (²⁴Na) quando attraversa il reticolo attivo.

Fino ad oggi non vi sono reattori LMFBR di tipo commerciale in esercizio. L'LMFBR di tipo sperimentale meglio riuscito è stato il francese Phenix, che sin dal luglio del 1974 fornisce regolarmente la potenza di 250 MWe. Si ritiene che il rapporto di fertilizzazione di un tipico reattore LMFBR raggiunga il valore di circa 1,15 ÷ 1,20 con un tempo di raddoppio (tempo necessario per raddoppiare l'inventario del materiale fissile) di circa 20 anni. Il tempo di raddoppio e il rapporto di fertilizzazione potrebbero essere migliorati se si sostituisse il sodio refrigerante con elio ad alta pressione, dal momento che l'elio non assorbe neutroni. Il reattore veloce autofertilizzante refrigerato a gas (GC FBR) è molto simile all'LMFBR, tranne, appunto, per il fatto che l'elio ad alta pressione sostituisce il sodio come refrigerante. Il reattore GCFBR per di più, oltre ad avere un rapporto di fertilizzazione più elevato, non presenta alcun incremento di reattività in caso di perdita del refrigerante: è perciò impossibile ottenere una reazione supercritica semplicemente mediante perdita del refrigerante, laddove nell'LMFBR, almeno per alcune configurazioni, l'espulsione del sodio potrebbe portare a un'escursione supercritica. Malgrado questi vantaggi, il GCFBR non rappresenta ancora una linea importante nello sviluppo degli autofertilizzanti.

Gli autofertilizzanti citati sopra lavorano con neutroni veloci; quelli termici, basati sul ciclo ²³³U-²³²Th, possono, in linea di principio, avere rapporti di fertilizzazione superiori a 1, ma solo se i prodotti di fissione che assorbono neutroni sono asportati continuamente dal reattore. Questa è l'idea che sta alla base del reattore autofertilizzante a sale fuso (MSBR). In questo sistema una soluzione fusa di ²³³UF₄-²³²ThF₄-⁷LiF-BeF₂ circola attraverso un blocco di grafite e successivamente attraverso lo scambiatore di calore. Mentre si trova nella grafite la soluzione subisce una reazione a catena, che si estingue quando la soluzione passa nello scambiatore di calore. Poiché il combustibile che subisce la reazione a catena è un liquido, esso può essere riprocessato in modo continuo per rimuovere i prodotti di fissione e l'²³³U prodotto. Il rapporto di fertilizzazione di questo sistema è solo di 1,07 circa; tuttavia, poiché l'inventario specifico di 2²³³U è di soli 1 ,5 kg/kW circa, mentre quello di un LMFBR è di 3 kg/kW di ²³⁹Pu, il tempo di raddoppio di un MSBR sarebbe uguale a quello di un LMFBR con rapporto di fertilizzazione di 1,14. Un piccolo reattore a sale fuso sperimentale è rimasto in funzione a Oak Ridge dal 1964 al 1969. Sebbene l'MSBR presenti alcuni problemi di corrosione, vi sono probabilmente buone ragioni per sviluppare questo sistema alternativo.

e) I reattori nucleari come parte del sistema energetico nucleare.

Un sistema energetico completo implica molto più della sola centrale elettrica. Per il carbone, ad esempio, esso comprende l'estrazione del minerale, il trasporto e la combustione del carbone e la sistemazione delle ceneri. A questo si deve aggiungere la purificazione del carbone, in particolare la rimozione dello zolfo, e la riduzione delle emissioni di particolati, per diminuirne i dannosi effetti sull'ambiente. In una economia basata sul carbone si devono trattare enormi quantità di materiale.

Il reattore nucleare, all'origine, fu visto semplicemente come sostituto della caldaia di una centrale a combustibile fossile. È divenuto invece evidente oggi che un sistema nucleare richiede molti stadi: l'arricchimento isotopico, la fabbricazione e il riprocessamento del combustibile, le separazioni chimiche e la sistemazione dei rifiuti. Sebbene le quantità di materiali in gioco siano decisamente molto minori che nel caso del carbone, a ogni stadio del processo si ha a che fare con materiali radioattivi pericolosi e, in qualche caso, estremamente pericolosi. L'economia di un sistema nucleare dipende dall'intero ciclo del combustibile. Questa connessione tra il reattore e il ciclo del combustibile può far sì che l'industria, che si è adattata ai combustibili fossili, si trovi nella necessità di subire alcuni cambiamenti strutturali per adeguarsi alle nuove tecnologie. Attualmente l'industria è molto frazionata e dispersa. Una possibilità attraente dell'era nucleare sarebbe quella di concentrare le parti più rischiose del ciclo, nonché le centrali di potenza, in grandi centri nucleari in cui effettuare la fabbricazione e il riprocessamento del combustibile, i processi chimici e il trattamento dei rifiuti. Una siffatta centralizzazione ridurrebbe fortemente i pericoli del trasporto e la possibilità di furto di materiale fissile e renderebbe più facile porre le parti più rischiose del ciclo sotto la direzione di specialisti dotati dell'esperienza necessaria per gestire le attività nucleari nel modo più intelligente. La trasmissione e la distribuzione dell'elettricità potrebbero essere effettuate come ora, se si tiene conto della crescente tendenza a collegare tra loro reti regionali o perfino nazionali.

5. Previsioni e prospettive.

a) Consumi e fonti energetiche.

L'umanità consuma, in media, energia a un tasso di 1,5 kW termici per persona. Ciò corrisponde a consumare carbone al tasso di 10¹⁰ tonnellate all'anno o petrolio al tasso di 3•10¹⁰ barili annui. L'uso che l'uomo fa di carbonio e idrogeno (che sono i principali costituenti del carbone e del petrolio) supera quello di qualsiasi altro minerale di almeno un fattore 3. Eppure l'abbondanza del combustibile fossile, che è di gran lunga la più importante sorgente di energia, è minima rispetto a quella di altre risorse naturali. La crosta terrestre contiene 10¹³ tonnellate di carbone e circa 0,02•10¹³. loli tonnellate di petrolio. Ciò corrisponde a un'abbondanza in peso, nella crosta terrestre, di carbonio e idrogeno ‛ridotti' di circa 16•10^-6, cioè pressappoco la stessa abbondanza del gallio. È straordinario che la risorsa minerale più usata dall'uomo, il combustibile fossile, sia uno dei materiali più rari che si trovano sulla Terra. È impossibile indicare quale sarà nel futuro il consumo di energia e prevedere così quando si esaurirà il combustibile fossile. Un esempio, tuttavia, può chiarire la situazione: negli Stati Uniti si consuma energia al tasso di 11kW pro capite, mentre in altre parti del mondo industrializzato se ne consuma al tasso di circa 4 kW pro capite. Se il mondo intero raggiungesse un tenore di vita eguale a quello dell'Occidente, corrispondente a 4 kW pro capite, e la popolazione del globo aumentasse fino a 10 miliardi di abitanti, il consumo mondiale di energia arriverebbe a circa 40•10⁹ kW. A questo livello il combustibile fossile del pianeta verrebbe consumato in circa 100 anni. I combustibili liquidi e gassosi sarebbero consumati molto prima: anche ai tassi attuali di consumo, potrebbero scomparire in 50 anni (v. energia: Fonti primarie di energia).

È chiaro che se l'uomo manterrà l'attuale società ad alta tecnologia e forti consumi energetici con i livelli di popolazione attuali o più elevati, avrà bisogno di fonti energetiche praticamente inesauribili. Le uniche significative possibilità che siamo oggi in grado di intravedere per queste fonti sono: la fusione controllata degli isotopi pesanti dell'idrogeno, l'energia geotermica, l'energia solare (compresi i suoi derivati, cioè il vento, le onde, i gradienti termici degli oceani, l'energia idroelettrica, i rifiuti dell'agricoltura) e il reattore autofertilizzante a fissione.

La fusione, che in ultima analisi vuol dire la conversione del deuterio del mare in elio, costituisce potenzialmente una fonte di energia estremamente grande, pari a 3•10¹⁷ megawatt-anno. Anche se ci si limita alla reazione deuterio-trizio, nella quale il trizio deve essere prodotto a partire dal poco abbondante ⁶Li, l'energia disponibile sarebbe ancora molto grande, eguale a circa 2,5•10¹⁴ megawatt-anno. Tuttavia non si è ancora riusciti a dimostrare la fattibilità della fusione, malgrado 25 anni di intensi sforzi in questo settore. Sebbene le proprietà del plasma si conoscano oggi molto bene e sia stato fatto un notevole progresso nel confinamento dei plasmi, siamo ancora molto lontani persino dal traguardo scientifico di ottenere le condizioni per produrre dalle reazioni di fusione tanta energia quanta se ne impiega per innescarle. Anche se si raggiungerà questo traguardo, le difficoltà tecnologiche saranno enormi. Pertanto non ci si può basare sulla fusione per il fabbisogno energetico a breve termine. Per quello a lungo termine ci si può affidare a innovazioni rivoluzionarie, del tipo rappresentato dai magneti superconduttori e dall'ignizione laser; per altre innovazioni si possono solo esprimere speranze, ma non formulare progetti. Se si otterrà la fusione, sarà una benedizione per il genere umano, ma non è possibile prevedere quanto tempo dovrà trascorrere prima di sapere se il processo sia realizzabile o no.

L'energia geotermica è attualmente utilizzata in molti posti ove vi sono zone calde vicino alla superficie della crosta terrestre. La maggior parte delle stime indicano che l'energia geotermica, così come quella idrica, difficilmente potrà soddisfare più di una piccola frazione dei bisogni totali di energia dell'umanità. Il flusso geotermico stazionario, cioè l'energia totale che fluisce dalle rocce, è d'altra parte estremamente diluito: 0,05 W/m². Il totale, che si ottiene integrando il flusso geotermico sulla superficie delle terre emerse del globo, è confrontabile con l'energia globale oggi consumata dall'uomo. Il problema dell'estrazione di questa energia da regioni non vulcaniche non è ancora stato risolto.

L'energia solare è utilizzabile e, com'è noto, è usata per riscaldare le case, per muovere imbarcazioni e mulini a vento, sotto forma di energia eolica, e, sotto forma di fotoni, per attivare la fotosintesi. Il flusso totale proveniente dal Sole corrisponde a circa 10.000 volte l'energia attualmente prodotta dall'uomo: una quantità enorme, anche se solo una piccola parte può essere convertita in vista di altri usi. Ma l'energia solare è diluita, in media circa 100 W/m², e la questione fondamentale è quella del suo costo. La maggior parte delle stime dà cifre comprese tra 50 e 80 millesimi di dollaro per kWh per centrali elettriche solari di grandi dimensioni (da confrontare con i 10-20 millesimi di dollaro per kWh per le centrali a carbone o a uranio), ma tali stime sono molto incerte.

La fissione basata sui comuni reattori convertitori, quali i reattori ad acqua che bruciano solo l'1% dell'uranio totale (con riciclo del Pu), è in realtà una risorsa piuttosto piccola. Ogni reattore LWR da 1.000 MWe con riciclo del Pu richiede circa 4.000 tonnellate di uranio naturale nel corso di 30 anni. Le riserve mondiali di uranio, al prezzo di 60 dollari/kg, sono valutate in 10⁷ tonnellate: tali riserve possono alimentare circa 2.500 LWR per 30 anni. Detto in altre parole, il contenuto energetico totale di tutto questo uranio utilizzato nei reattori convertitori è all'incirca eguale all'energia ottenibile dalle attuali riserve di petrolio: 2•10¹⁵ kWh.

A concentrazioni inferiori, e quindi a prezzi più alti, sono disponibili quantità molto maggiori di uranio e di torio. Ma se i reattori usano solo l'1% dell'uranio (e del torio), lo sfruttamento di giacimenti più poveri diventa antieconomico. È stato calcolato che con giacimenti che contengono 10 ppm l'energia necessaria per estrarre l'uranio è grosso modo eguale all'energia che si ottiene bruciando l'uranio in un reattore convertitore. Molto prima di arrivare a tali giacimenti di bassa qualità, il costo dell'energia e il danno all'ambiente provocato dal trattamento di così grandi quantità di minerali renderebbero quasi sicuramente inaccettabile l'energia nucleare basata sui convertitori.

Il reattore autofertilizzante a fissione, d'altra parte, permette di utilizzare come combustibili il torio e l'uranio residui presenti nella crosta terrestre (circa 10 ppm). Il reattore autofertilizzante estrae dall'uranio e dal torio 60 volte più energia di quella fornita dal reattore convertitore. Così per il reattore autofertilizzante si possono sfruttare giacimenti 60 volte meno ricchi di quelli utilizzati per il reattore convertitore. Per esempio, a 10 ppm il rendimento energetico di un reattore autofertilizzante è ancora di 50 a 1. Al tasso di consumo energetico ipotizzato nel nostro esempio, 40•10⁹ kW, verrebbero usate solo 1.500 tonnellate di uranio e torio all'anno. Con concentrazioni di 10^-6 ciò richiederebbe la lavorazione di 1,5•10⁹ tonnellate di materiale, il che equivale circa all'attuale produzione annua mondiale di carbone e non dovrebbe rappresentare un carico inaccettabile per l'ambiente. (In ambedue i casi la quantità di materiale da trattare è un po' più grande. Per l'uranio e il torio l'efficienza di estrazione sarà inferiore al 100%, mentre per il carbone occorre aggiungere i sovraccarichi e le miscele non combustibili).

La riserva disponibile dovrebbe essere una frazione non trascurabile della crosta terrestre. Sembra chiaro, dunque, che il reattore autofertilizzante, ‛bruciando le pietre', potrebbe fornire all'uomo una fonte di energia praticamente inesauribile. Inoltre, poiché il reattore autofertilizzante usa il proprio combustibile con tanta efficienza, i relativi costi di produzione di energia sono assai poco sensibili al prezzo dell'uranio greggio e dovrebbero essere paragonabili a quelli che noi paghiamo attualmente per l'elettricità prodotta dai reattori ad acqua, cioè circa 20 millesimi di dollaro per kWh.

In tempi relativamente brevi l'umanità certamente sfrutterà al massimo i combustibili fossili e le altre fonti accessibili. Sui tempi lunghi i possibili candidati per il nostro sistema energetico sono la fusione, l'energia solare e i reattori a fissione autofertilizzanti. La fattibilità della fusione non è stata ancora dimostrata e la relativa tecnologia non può ancora essere pienamente valutata. L'energia solare è sostanzialmente non inquinante e generalmente ‛benigna', ma è molto costosa e la sua tecnologia è ancora in una fase immatura. La terza possibilità, il reattore a fissione autofertilizzante, corrisponde a una tecnologia quasi completamente sviluppata e promette costi dell'energia paragonabili a quelli attuali. D'altro canto bisogna ammettere che un'economia basata sugli autofertilizzanti presenta alcuni rischi. Questa situazione ci porta alla domanda cruciale: può l'umanità convivere con la fissione?

b) L'umanità può convivere con la fissione?

In un certo senso l'umanità si è impegnata a occuparsi dell'energia nucleare quando ha sviluppato le armi nucleari e fin dai primi giorni dell'era atomica il problema di ‟come vivere con la bomba" ha preoccupato l'opinione pubblica e gli uomini politici. Solo recentemente, tuttavia, la scelta dei reattori nucleari come sorgente fondamentale di energia, con tutte le sue implicazioni, ha posto la questione con più grave urgenza. Per rispondere alla domanda se l'uomo può convivere con la fissione è necessario affrontare i problemi concernenti: 1) gli effetti di radiazioni di basso livello generate dai sistemi energetici; 2) la possibilità di incidenti nei reattori; 3) la possibilità di furto di materiale fissile per la fabbricazione clandestina di bombe atomiche; 4) lo smaltimento dei rifiuti radioattivi.

1. Emissioni radioattive di basso livello nell'esercizio normale dei reattori. - Piccole quantità di radioattività vengono rilasciate anche da un reattore che funzioni regolarmente. Tuttavia gli scarichi di routine sono attualmente limitati a 5-10 millirem/anno negli Stati Uniti e a qualcosa di più in altri paesi, laddove il fondo naturale è in genere attorno a 100 millirem/anno (ma in alcuni luoghi è 10 volte più alto). Con dei livelli così bassi di radiazione totale e media non vi è alcuna prova che la radiazione possa provocare qualche danno biologico. Sebbene sia prassi supporre, per prudenza, che gli effetti biologici siano proporzionali alla dose fino a valori nulli di questa (ipotesi lineare e senza soglia), l'evidenza di cui si dispone indica che tale ipotesi sovrastima, e probabilmente di molto, il rischio di danni da radiazione. Vi sono sulla Terra luoghi popolati (a grandi altezze o in zone con formazioni granitiche) dove il fondo naturale di radiazione supera di molto la media nonché le emissioni di routine previste in una centrale nucleare. Non è stato osservato alcun effetto di questa radiazione di fondo più elevata sulla salute della popolazione, pur tenendo conto del fatto che tali effetti possono essere difficili da quantificare. È certo, in ogni caso, che il normale esercizio dei reattori nucleari presenta un rischio piccolo o addirittura nullo.

2. Possibilità di incidenti nei reattori. - Anche dopo che un reattore da 1.000 MWe è stato spento, i prodotti di fissione radioattivi continuano a generare circa 200 MW di calore, che vanno gradualmente diminuendo. Dopo un giorno il calore prodotto scende a 15.000 kW e dopo 60 giorni a 2.000 kW. Perciò un reattore di elevata potenza dev'essere raffreddato per convezione forzata fino a che la produzione di calore non sia scesa al livello in cui il calore può essere asportato per convezione naturale; diversamente, il combustibile fonderebbe. Per questo motivo i reattori di alta potenza sono in genere provvisti di sistemi di refrigerazione di emergenza (ECCS). Gli ECCS debbono sommergere d'acqua il nocciolo nel caso che il sistema di refrigerazione normale non funzioni, per esempio in conseguenza di una rottura nella linea principale di adduzione del refrigerante al reattore. Oltre agli ECCS i reattori sono provvisti di molti altri sistemi di emergenza per ridurre la probabilità che il sistema di refrigerazione si possa guastare o che si possa perdere il controllo della reazione a catena (sebbene un'esplosione del tipo di quella atomica sia impossibile) o per confinare la radioattività in caso di incidente. La maggior parte dei reattori moderni costruiti in Occidente sono alloggiati in grandi recipienti di acciaio: il recipiente dovrebbe trattenere qualsiasi ammontare di radioattività che eventualmente sfuggisse dal reattore.

Quando furono introdotti i recipienti di contenimento per i reattori ad acqua leggera, si credeva che tali recipienti non si potessero rompere, qualunque cosa accadesse al reattore. Tuttavia, con l'aumentare delle dimensioni dei reattori, questa convinzione divenne insostenibile. La maggior parte delle perdite accidentali di un reattore sarebbe limitata dal recipiente di contenimento, tuttavia la fusione totale di un reattore da 1.000 MWe darebbe luogo alla ‛sindrome cinese', il passaggio della massa fusa attraverso il recipiente. Non si poté dunque più garantire in modo assoluto la sicurezza di un grande reattore: piuttosto ci si dovette affidare al fatto che la probabilità di incidenti è estremamente bassa ed ancora minore è quella che i sistemi di emergenza non funzionino come previsto. Questi problemi sono stati studiati in modo completo da un gruppo di studio apposito, promosso dalla U.S. Atomic Energy Commission e diretto dal professor N. Rasmussen, che è giunto alla conclusione che la probabilità di una fusione con rottura del sistema di contenimento è di circa 1 su 17.000 per anno, che solo il 10% di tali incidenti darebbe luogo a casi mortali e che la probabilità di una catastrofe immensa, con diverse migliaia di persone uccise e ingenti danni alle cose, è estremamente bassa, inferiore a 1 su 10 milioni per anno, forse eguale a 1 su un miliardo per anno.

L'analisi di Rasmussen si riferisce ai reattori ad acqua leggera. Studi di questo tipo sono complessi, lunghi e costosi. È assolutamente necessario che si intraprenda uno sforzo corrispondente anche per i reattori autofertilizzanti. Tuttavia le analisi, meno complete, fatte sino ad ora non forniscono alcuna ragione per sospettare che la situazione degli autofertilizzanti sia significativamente diversa da quella dei reattori ad acqua leggera.

È difficile fare assegnamento sui numeri esatti che scaturiscono dall'analisi di sistemi così complessi. I problemi sono, in un certo senso, metascientifici, cioè, sebbene possano essere formulati in termini scientifici, la risposta trascende le capacità della scienza. Uno dei modi per affrontare tali questioni di rischio ipotetico è di paragonare la pericolosità presunta di un reattore nucleare con l'esperienza che l'uomo ha acquisito con altri grandi generatori di energia, in particolare con le dighe. Il professor D. Okrent ha stimato che la diga di Folson sull'American River sopra la città di Sacramento in California ha una probabilità compresa tra 1 su 100 e i su 1.000 all'anno di essere distrutta da un terremoto: se ciò dovesse avvenire, potrebbero perire circa 200.000 persone. Catastrofi causate dalla rottura di dighe fanno parte dell'esperienza degli uomini: circa 2.000 persone annegarono in seguito alla gigantesca frana che dal monte Toc cadde nell'invaso della diga del Vajont nel 1963.

Non si sono mai verificati incidenti di tale portata nell'impiego dei reattori né alcun individuo è stato mai danneggiato a causa della radioattività proveniente da un reattore guasto. Eppure la radioattività è un rischio che l'uomo non ha accettato, proprio come, nei primi tempi dell'elettricità, molta gente era restia ad accettare il pericolo dell'elettrocuzione, malgrado gli evidenti vantaggi dell'energia elettrica.

3. Possibilità di furto di materiale fissile per la fabbricazione clandestina di bombe atomiche. - Un mondo impostato sull'energia nucleare, con consumo annuo di 40•10⁹ kW richiederebbe 8.000 reattori autofertilizzanti, ognuno da 5.000 MW termici. L'inventano di plutonio di questi reattori sarebbe di circa 15.000 tonnellate e il sistema ogni anno aumenterebbe di circa 100 tonnellate la riserva mondiale di plutonio.

Con una così larga diffusione del plutonio, qual è la probabilità che dei terroristi ne possano trafugare una parte per fabbricare bombe atomiche rudimentali? Questo non è un problema propriamente tecnico, nè può ricevere una risposta precisa. Sono stati presi degli accorgimenti per ridurre la probabilità di furto. In tutti i punti vulnerabili del ciclo del combustibile il materiale fissile è strettamente sorvegliato, almeno negli Stati Uniti. Inoltre l'Agenzia Internazionale per l'Energia Atomica (AIEA) ispeziona i reattori per garantire che non venga sottratto materiale fissile: la maggior parte dei paesi attualmente in possesso di reattori nucleari è sottoposta alle ispezioni dell'AIEA. Ciò nonostante, come per gli incidenti, è difficile escludere in assoluto ogni possibilità di furto. Un modo per diminuire i rischi di furto, che presenta anche il vantaggio di ridurre al minimo il tragitto del materiale fissile, consiste nel raggruppare i reattori e i loro impianti chimici in pochi centri di energia nucleare; tali centri potrebbero essere sottoposti a severa sorveglianza.

4. Eliminazione dei rifiuti. - Un reattore da 1.000 MWe all'equilibrio contiene circa 10¹⁰ curie di prodotti di fissione radioattivi. Tale reattore produce ogni anno 10⁷ curie di rifiuti radioattivi a lunga vita e, all'equilibrio, le scorie di un sistema energetico mondiale che produca 40•10⁹ kW sarebbero pari a 3•10¹² curie. Di per sè il volume di questi materiali radioattivi è piccolo, circa 200 litri/anno per reattore. In pratica, tuttavia, questi materiali si trovano diluiti con materiale chimico inerte che ne fa aumentare il volume; anche tenendo conto di questo il volume totale dei rifiuti rimane sorprendentemente piccolo.

Fra i prodotti di fissione i più importanti sono il ¹³⁷Cs e lo ⁹⁰Sr, che hanno un tempo di dimezzamento di circa 30 anni e rimangono molto pericolosi per circa 500 anni. Insieme ai rifiuti vi sono piccole quantità di elementi pesanti a vita molto più lunga, gli attinidi, e in particolare il plutonio, che rimangono pericolosi per diverse centinaia di migliaia di anni. Sorge allora il problema fondamentale di cosa fare con i crescenti rifiuti radioattivi dell'impresa nucleare.

La proposta più accettabile è quella di solidificare i rifiuti in ceramica o vetro non lisciviabili e poi segregarli in qualche formazione geologica, per esempio in depositi di sale. Tali depositi sono in genere molto asciutti (altrimenti si sarebbero dissolti da molto tempo); molti di loro sono rimasti stabili a partire dal Permiano. Il sale inoltre fluisce in modo plastico, quindi i bidoni di rifiuti radioattivi immersi nel sale verrebbero seppelliti dal sale in movimento.

È necessaria una sorveglianza perpetua dei depositi di materiali radioattivi? Se per esempio, mentre si fanno prospezioni per la ricerca di petrolio, si esegue una trivellazione nel sale, è possibile pensare che i letti di sale vengano allagati da acqua proveniente da falde meno profonde. Sebbene si possa presumere che anche in questa eventualità il rischio sarebbe minimo - in parte perchè il moto dell'acqua è lento, in parte perché è assai difficile che i rifiuti vengano lisciviati - queste sono, ancora una volta, questioni difficili da definire in modo certo.

Il fatto che i reattori del Gabon abbiano funzionato, in tempi geologici antichi, senza che sia avvenuta alcuna mi- grazione del plutonio costituisce un'ottima prova della capacità della Terra di accogliere i rifiuti provenienti dai reattori nucleari. Inoltre è possibile, in linea di principio, trasmutare dentro i reattori gli attinidi in prodotti di fissione che diventano innocui dopo 500 anni. Per dare un'i- dea della dimensione del problema bisogna tener presente che la Terra contiene già enormi quantità di materiali radioattivi: ogni metro quadrato della crosta terrestre con- tiene, in media, 10^-2 curie di radio e le terre emerse contengono 10¹² curie di radio. Perciò, anche se non si può affermare con assoluta certezza che non sarà necessaria alcuna sorveglianza particolare per i rifiuti radioattivi, sembra ragionevole supporre che le misure di sicurezza potranno limitarsi al divieto d'accesso ai relativi depositi.

Bibliografia.

Clark, S. H., World energy, Menlo Park, Cal., 1972.

Hewlett, R. G., Anderson, O.E., The new world 1939-1946. A history of the United States Atomic Energy Commission, vol. I, University Park, Penn., 1962.

Hubbert, M. K., Energy resources, in Resources and man (a cura del National Research Council Committee on Resources and Man), San Francisco 1969, cap. VIII, pp. 157-242.

??? Le phénomène d'Oklo, in ‟Bulletin d'informations scientifiques et techniques", 1974, 193.

Penner, S. S., Icerman, L., Energy, 3 voll., Reading Mass., 1974 ss.

Petrosyants, A. M., From scientific search to amic industry: modern problems of atomic science and technology in the USSR, Danville, Ill., 1975.

Szilard, L., The collected work of Leo Szilad (a cura di B. T. Feld e G. W. Szilard), Cambridge, Mass., 1972, pp. 605-651.

U.S. Atomic Energy Commission, An assessment of accidents risks in U.S. commercial nuclear power plants, report n. WASH-1400, gosto 1974.

U.S. Atomic Energy Commission, High-level radioactive waste management alternatives, report n. WASH-1297, maggio 1974.

Vandenbosch, R., Huizenga, J. R., Nuclear fission, New Yok 1973.

Weinberg, A. M., Wigner, E.P., The physical theory of neutron chain reactors, Chicago 1958.

Willrich, M., Taylor, Th. B., Nuclear theft: risks and safeguards, Cambridge, Mass., 1974.

Armi nucleari

SOMMARIO: 1. Introduzione: a) armi a fissione nucleare; b) armi termonucleari; c) guerra nucleare. □ 2. I fondamenti scientifici delle armi nucleari. □ 3. Alcune caratteristiche particolari delle armi nucleari. □ 4. Effetti di una guerra nucleare totale. □ Bibliografia.

1. Introduzione.

a) Armi a fissione nucleare.

La prima bomba a fissione del mondo fu fatta esplodere poco prima dell'alba del 16 luglio 1945 su una torre eretta in una regione desertica nei pressi di Alamogordo, nel Nuovo Messico. Per giungere a questo risultato era stato necessario risolvere un gran numero di problemi tecnici senza precedenti e allestire e collaudare impianti di concezione assolutamente nuova. All'impresa, che costò circa due miliardi di dollari, parteciparono decine di migliaia di persone.

L'energia liberata nella prima esplosione nucleare equivaleva a quella sprigionata dall'esplosione di 20 milioni di chilogrammi (20 chilotoni) di TNT. Questa energia (comunemente nota col termine inglese yield, ‛resa') era fornita dalla fissione dei nuclei di poco più di un kg di un nuovo elemento artificiale: il plutonio (Pu). Poiché solo una modesta frazione del Pu presente sarebbe stata effettivamente utilizzata nella reazione, l'ordigno doveva contenerne parecchi chilogrammi. I materiali accessori, come l'esplosivo ad alto potenziale necessario a innescare la reazione, i componenti elettrici e la custodia dell'arma, pesavano circa 4.500 kg ed erano contenuti in un involucro che poteva essere sganciato da un bombardiere pesante.

La prima utilizzazione bellica di un'arma nucleare devastò la città di Hiroshima il 6 agosto 1945. La seconda distrusse la città di Nagasaki il 9 agosto 1945. Cinque giorni dopo finiva la seconda guerra mondiale con la resa del Giappone.

Il bombardamento atomico di Hiroshima causò 70.000 morti, quello di Nagasaki 40.000; spesso si citano questi dati per illustrare la potenza distruttiva delle armi nucleari. Tuttavia un maggior numero di morti avevano provocato singole azioni aeree compiute nel corso della seconda guerra mondiale: oltre 80.000 vittime a Tōkyō nel marzo 1945 e, probabilmente, più di 100.000 a Dresda nel febbraio dello stesso anno. Benché la quantità di radiazioni ionizzanti liberate dalle esplosioni nucleari sia stata altissima, l'onda d'urto e il calore sviluppato provocarono, fra i sopravissuti all'esplosione, un numero di vittime doppio rispetto alle radiazioni. La capacità distruttiva delle prime armi nucleari fu principalmente dovuta all'elevato rapporto tra forza esplosiva e peso, per cui, con una singola bomba, si poterono ottenere effetti su vasta scala.

I massicci attacchi aerei della seconda guerra mondiale, nei quali si impiegavano esplosivi convenzionali e bombe incendiarie e che provocarono un gran numero di morti fra la popolazione civile, richiedevano stormi di alcune o addirittura di molte centinaia di bombardieri. Un singolo bombardamento durava parecchie ore e spesso buona parte degli aerei attaccanti veniva abbattuta nel corso della missione. Con le prime armi nucleari si potè ottenere lo stesso effetto distruttivo con una sola bomba trasportata da un solo aereo. Così divenne all'improvviso terribilmente facile infliggere gli stessi gravissimi danni per provocare i quali, in precedenza, erano necessarie le ingenti risorse belliche di una grande potenza.

A partire dal 1945 gli Stati Uniti hanno fatto esplodere, fra bombe a fissione e bombe termonucleari, almeno sei o settecento cariche nucleari di prova. Nella maggioranza dei casi la categoria di appartenenza degli ordigni non è stata resa nota; però almeno per i due terzi di queste esplosioni la forza esplosiva era contenuta nella parte bassa della scala nucleare - non più di poche decine di chilotoni - caratteristica delle armi a fissione. Indubbiamente molti di questi collaudi sono serviti per mettere a punto qualche particolare tipo di arma, altri per ottenere informazioni sulle conseguenze dell'esplosione: l'effetto dell'onda d'urto su strutture e attrezzature, la formazione del cratere, l'effetto dell'esplosione a grande altezza. In seguito a questi 400 collaudi circa, gli Stati Uniti hanno realizzato un arsenale nucleare comprendente armi a fissione perfettamente sperimentate, la cui forza esplosiva va da meno di un chilotone a parecchie centinaia di chilotoni, il cui peso è compreso fra i 25 kg e i 4.500 kg del primo esemplare e il cui diametro varia da meno di 20 cm ai 150 cm del prototipo. In genere le armi di peso e misura inferiore sviluppano una minore forza esplosiva. Oltre alle bombe per distruggere le città sono stati messi a punto modelli di ordigni nucleari anticarro, antisommergibile, antiaereo, ecc. Sono previsti diversi sistemi di lancio: gli ordigni nucleari possono essere sganciati da grandi bombardieri a lungo raggio, come avvenne per i due primi esemplari, oppure possono essere lanciati come proiettili di artiglieria, essere trasportati da piccoli missili vettori a breve raggio o da piccoli cacciabombardieri. Secondo una valutazione dello Stockolm International Peace Research Institute, SIPRI (v., 1978), l'arsenale degli Stati Uniti comprende attualmente parecchie decine di migliaia di armi nucleari.

A partire dal 1945 parecchi altri paesi hanno costruito e sperimentato ordigni nucleari (termonucleari e a fissione), acquisendo così l'esperienza necessaria a realizzare armi a fissione diverse per dimensioni e prestazioni. Anche in questi casi il modello dell'ordigno sperimentato è stato comunicato solo di rado, ma dalle vaghe dichiarazioni rilasciate (del tipo ‟arma dotata di bassa forza esplosiva") è ragionevole supporre che la maggior parte delle prove sia stata effettuata con armi a fissione. Il SIPRI ha pubblicato il seguente elenco di paesi che hanno condotto esperimenti nucleari entro il 1977: Stati Uniti (626 esperimenti a partire dal luglio 1945), Unione Sovietica (371 esperimenti a partire dall'agosto 1949), Gran Bretagna (27 esperimenti a partire dall'ottobre 1952), Francia (70 esperimenti a partire dal febbraio 1960), Cina (22 esperimenti a partire dall'ottobre 1964). Tutti questi paesi, tranne la Gran Bretagna, hanno effettuato ulteriori esperimenti dopo il 1977. Benché il numero degli esperimenti condotti sia da mettersi più direttamente in relazione con la varietà delle armi cui un paese è interessato che con l'effettivo numero di armi di cui dispone, tuttavia tale numero è pur sempre un indice dell'entità delle risorse dedicate al programma di armamento e può di conseguenza fornire un'indicazione, almeno approssimativa, dell'ammontare delle riserve di armi nucleari. Su queste basi si può calcolare che il numero di armi a fissione che costituiscono gli arsenali delle varie potenze nucleari, ad eccezione degli Stati Uniti, sia dell'ordine delle decine di migliaia; si ritiene che circa il 75% di queste riserve appartengano all'Unione Sovietica.

Nel maggio del 1974 anche l'India ha fatto esplodere un ordigno a fissione, la cui forza esplosiva si aggirava intorno ai 10-15 chilotoni. Il governo indiano ha insistito nel dichiarare di non essere interessato alle armi nucleari, ma solamente all'impiego pacifico delle esplosioni nucleari, che possono essere utilizzate, per esempio, per spostare grandi quantità di terra. Finora l'India non ha effettuato altri esperimenti, nè ha dato segno di accumulare un arsenale nucleare; ma non vi è dubbio che, se decidesse di farlo, sarebbe in grado di costruire armi nucleari seguendo il modello già sperimentato. Oltre ai paesi citati ne esistono molti altri che dispongono delle capacità tecnologiche e delle risorse industriali necessarie per produrre armi a fissione: tutte le nazioni industrializzate europee, il Giappone, Israele, il Sudafrica e altri.

Le informazioni fondamentali concernenti le reazioni nucleari, il comportamento e il trattamento dei materiali, la produzione, le proprietà fisiche e chimiche del plutonio, ecc. sono ormai di dominio pubblico. Benché la produzione di un'arma nucleare implichi un impegno economico e tecnologico non indifferente - pari a quello richiesto per la costruzione di un aereo a reazione - per molti paesi il principale argomento a sfavore di un'iniziativa del genere è di ordine politico più che tecnico-scientifico o finanziario.

b) Armi termonucleari.

Il fenomeno della fissione dell'uranio, il più pesante degli elementi naturali, fu scoperto negli ultimi mesi del 1938, ma già da alcuni anni ci si era resi conto che l'energia del Sole proviene da reazioni nucleari nelle quali i nuclei di elementi leggeri si agglomerano o si fondono. Perché tali reazioni di fusione possano avvenire, è necessario che i nuclei implicati collidano a velocità relative estremamente elevate; all'interno della materia ciò può avvenire solo a temperature molto alte, superiori a 10 milioni di gradi centigradi, quando per l'agitazione termica dei nuclei si raggiungono velocità dell'ordine di grandezza necessario. Per questo motivo, l'emissione di energia ottenuta in questo processo è detta ‛termonucleare'.

Le temperature necessarie alla fusione sono di gran lunga superiori a quelle di qualsiasi fenomeno riscontrabile sul nostro pianeta o ottenibile mediante il più intenso processo di combustione chimica; ma l'avvento degli esplosivi a fissione, con le loro alte concentrazioni di energia, dischiuse la possibilità di ottenere temperature proprio dell'ordine di grandezza necessario a dare inizio a reazioni termonucleari. Si saggiò quindi la possibilità di servirsi di queste nuove elevate temperature per accendere una massa di combustibile termonucleare. Eccettuata l'India, che non ha condotto esperimenti nucleari volti a questo scopo, tutti i paesi che hanno collaudato armi a fissione, sono riusciti a produrre e sperimentare con successo anche armi termonucleari.

Da un punto di vista pratico, i principali vantaggi del combustibile termonucleare, rispetto al materiale fissile usato nelle armi a fissione, sono i seguenti.

È relativamente assai meno costoso. Il deuterio, l'isotopo pesante dell'idrogeno, uno dei componenti principali dei combustibili termonucleari utilizzati nelle armi, costa all'incirca 1 dollaro al grammo, in confronto ai 40 dollari al grammo del plutonio, mentre l'energia ottenibile da I grammo di deuterio completamente consumato sarebbe pari a circa 3 volte l'energia ottenibile dalla stessa quantità di plutonio completamente fissionato. Le scorte di deuterio sono virtualmente inesauribili, dal momento che sulla Terra c'è circa 1 atomo di deuterio per ogni 6.000 atomi di idrogeno nell'acqua.

Infine il combustibile nucleare (sia il deuterio puro, sia i suoi composti, per esempio quello con il litio) può essere accumulato senza alcun pericolo in quantità arbitrariamente grandi, dal momento che non si hanno reazioni violente finché non è portato a elevatissime temperature. Al contrario, bisogna usare moltissime cautele quando si maneggiano grandi quantità di materiale fissile, poiché si potrebbe avere una reazione violenta, a causa della natura stessa del materiale, se tale quantità superasse una certa soglia critica. Di conseguenza, le armi termonucleari appaiono particolarmente vantaggiose se si vogliono costruire armi nucleari dotate di una forza esplosiva molto maggiore di quella di fissione richiesta per l'innesco. Benché, in generale, le forze esplosive non debbano necessariamente essere particolarmente elevate, in linea di principio esse possono raggiungere qualunque intensità. Per alcuni scopi, come nel caso di armi da usare nelle vicinanze delle proprie truppe, navi o aereoplani, una forza esplosiva molto grande può risultare non conveniente. In molti casi i limiti di potenza delle armi termonucleari coincidono con i limiti di volume e di peso compatibili con la capacità del mezzo che le trasporta.

La prima grande esplosione termonucleare fu ottenuta dagli Stati Uniti, a titolo sperimentale, nel novembre del 1952 nell'atollo di Eniwetok. La forza esplosiva fu di circa 10.000 chilotoni (o 10 megatoni). Di lì a poco, l'Unione Sovietica (agosto 1953) fece esplodere il suo primo ordigno termonucleare, seguita dalla Gran Bretagna nel 1957, dalla Cina nel 1967 e dalla Francia nel 1968.

Dopo i primi tentativi, tutti questi paesi hanno fatto esplodere altri modelli termonucleari con l'obiettivo di migliorarne le prestazioni, di accertare la validità dei progetti su diverse scale di potenza e di dimensioni e di adattare i modelli ai nuovi metodi di trasporto. Gli Stati Uniti e l'Unione Sovietica, in particolare, con il loro grande assortimento di missili e di altri vettori, hanno condotto un gran numero di esperimenti termonucleari. Nel caso di bersagli localizzati è desiderabile disporre di un'arma dotata di potenza distruttiva sufficiente per distruggere il bersaglio anche nel caso che il mezzo vettore lo manchi per un errore di mira standard. I miglioramenti ottenuti nella tecnica di guida dei missili a lungo raggio hanno considerevolmente ridotto gli errori di mira, tanto che ora si ritengono sufficienti potenze esplosive relativamente modeste. Per questo e per altri motivi sia gli Stati Uniti sia l'Unione Sovietica stanno sostituendo le grandi testate singole di alcuni loro missili con un certo numero (da 3 a 10) di armi più piccole, chiamate vettori a rientro multiplo (Multiple Reentry Vehicles, MRV) o vettori a rientro multiplo indirizzabili indipendentemente (Multiple Independently Targetable Reentry Vehicles, MIRV). Per mettere a punto queste armi termonucleari leggere e di forza esplosiva relativamente bassa, è probabile che siano state necessarie molte prove.

Stando alle notizie diffuse, l'ordigno termonucleare più potente collaudato dagli Stati Uniti (nel 1954) fu da 15 megatoni, mentre l'Unione Sovietica ha fatto esplodere una carica termonucleare da 60 megatoni (nel 1961). In ogni modo pare che attualmente le armi più grandi degli arsenali degli Stati Uniti e dell'Unione Sovietica siano meno potenti e molto più leggere. Nel 1977 il SIPRI effettuò una stima del potenziale esplosivo delle armi strategiche, cioè di quelle armi che vengono trasportate o da missili balistici intercontinentali (Inter Continental Ballistic Missiles, ICBM) o da missili balistici lanciati da sottomarini (Submarine-Launched Ballistic Missiles, SLBM) o da bombardieri a lungo raggio. Secondo l'elenco del SIPRI la forza esplosiva delle testate termonucleari americane era compresa tra 10 megatoni e 40 chilotoni circa, quella delle armi sovietiche tra 20 megatoni e 200 chilotoni circa. Il numero di testate strategiche termonucleari che gli Stati Uniti erano in grado di lanciare era prossimo alle 12.000 unità. Più della metà di queste erano del tipo MIRV e la forza esplosiva media per ciascuna arma dell'intero arsenale era di circa 0,5 megatoni. L'Unione Sovietica disponeva di circa 4.400 testate strategiche termonucleari, con una minor quota di MIRV, aventi una forza esplosiva media vicina ai 2 megatoni. Bisogna considerare che una stima del genere si fonda su numerose deduzioni e illazioni, dato che le informazioni necessarie per avere un quadro preciso sono mantenute segrete. Malgrado ciò, si dispone di un certo numero di informazioni dirette, riguardo al numero dei missili dei diversi tipi, alle dimensioni, alla forma e alle capacità di trasporto dei vettori, e indirette, ricavabili, per esempio, dai dati del bilancio, che garantiscono l'attendibilità, sia pure approssimativa, della stima effettuata.

Recentemente (1979) si sono conclusi i negoziati tra Stati Uniti e Unione Sovietica per la stipula di un nuovo trattato per la limitazione delle armi strategiche (SALT II): il numero totale dei vettori strategici (circa 2.400 per parte) dovrebbe rimanere quasi invariato nei successivi 7 anni circa. Tuttavia, anche in questo caso, dato l'aumento della produzione dei vettori MIRV, il numero totale delle armi termonucleari continuerebbe a salire.

È relativamente facile costruire una bomba a fissione: se si riesce a far sì che il meccanismo di innesco porti il materiale fissile in una configurazione supercritica, si può esser certi che la bomba funzionerà. Non è altrettanto semplice prevedere la potenza di un simile ordigno; volendo conoscere con esattezza l'entità della forza esplosiva di una bomba a fissione è necessario collaudarla.

Come abbiamo già spiegato, per dare inizio a una reazione termonucleare bisogna ricorrere a un congegno di innesco a fissione. Non basta sapere, in questo caso, che il meccanismo a fissione esploderà; infatti è necessario sapere non solo come funziona nei dettagli, ma anche se, con la sua azione, sarà in grado di innescare almeno una parte del combustibile termonucleare. I principi che regolano l'innesco di una reazione termonucleare sono molto più complessi di quelli in base ai quali una certa quantità di materiale fissile raggiunge una configurazione supercritica. Per sapere quando una certa quantità di materiale fissile dicenterà supercritica non è necessario raggiungere la criticità, basta calcolare quanto rapidamente ci si avvicini a tale condizione; invece, per sapere se il combustibile termonucleare brucerà bisogna portarlo effettivamente alla temperatura richiesta. In altre parole, mentre la messa a punto di un'arma a fissione non implica necessariamente l'effettuazione di collaudi ed esperimenti, nel caso di un'arma termonucleare queste prove sono indispensabili.

Per quanto riguarda le prime bombe atomiche, le distanze alle quali i tre effetti principali dell'esplosione (onda d'urto, effetto termico, radiazione istantanea) erano altamente pericolosi, o addirittura letali, praticamente coincidevano, aggirandosi intorno al valore di 1,5 km. Per un'esplosione nucleare 100 volte maggiore (quale può essere provocata da una bomba termonucleare da 2 megatoni) le distanze corrispondenti sarebbero di circa 7,11 e 3 km, rispettivamente. La ragione per cui il raggio della zona colpita dalle radiazioni aumenta tanto meno degli altri è da attribuirsi al fatto che l'intensità delle radiazioni si attenua secondo una legge esponenziale, diminuendo di un fattore 100 in meno di 1,5 km, mentre il raggio della zona devastata dall'onda d'urto cresce con la radice cubica della forza esplosiva e il raggio della zona entro cui si fa sentire l'effetto termico non cresce con la radice quadrata della forza esplosiva, come si potrebbe prevedere, ma meno rapidamente, in quanto l'impulso termico causato dalle esplosioni maggiori risulta distribuito su un tempo più lungo.

L'esplosione di un ordigno termonucleare è quindi in grado di causare un numero di vittime da 20 a 50 volte maggiore di quello provocato dalle esplosioni delle prime bombe atomiche; questo enorme potenziale distruttivo si realizza principalmente attraverso l'onda d'urto e l'effetto termico. Le radiazioni istantanee, infatti, rappresentano una causa relativamente trascurabile di mortalità immediata. Così, nel caso che una città fosse attaccata con una sola arma termonucleare da 2 megatoni, il numero delle vittime potrebbe ammontare ad alcuni milioni. Questo livello di distruzione è di gran lunga più alto di quello raggiunto sia dalle prime bombe atomiche sia dai più massicci bombardamenti aerei effettuati nel corso della seconda guerra mondiale. Il numero delle vittime potrebbe superare di molto quello provocato da un qualsiasi disastro naturale della storia recente, come il ciclone che nel 1970 colpì il Pakistan orientale (circa 500.000 morti) o l'alluvione del Hwang Ho (Fiume Giallo) del 1887 (oltre 900.000 vittime), potendosi paragonare al numero dei caduti, nel corso della seconda guerra mondiale, dei principali paesi belligeranti, come il Giappone (circa 1,5 milioni di morti) o la Germania (quasi 3 milioni di caduti). L'effetto letale di un'esplosione termonucleare sarebbe superato solo da pochi casi di pestilenze o epidemie, come la peste nera del XIV secolo o l'epidemia di influenza del 1917-1918, che causò 20-30 milioni di vittime. Basterebbe comunque una dozzina di bombardamenti termonucleari per raggiungere simili livelli di mortalità e gli arsenali americano e sovietico contengono ben più di qualche dozzina di ordigni termonucleari; inoltre, mentre il pericolo rappresentato dalle pestilenze può dirsi stornato, almeno su vasta scala, la minaccia nucleare è tuttora incombente.

c) Guerra nucleare.

In questo paragrafo saranno illustrate schematicamente alcune congetture circa l'andamento di un'eventuale guerra nucleare.

Quando si pensa alla guerra nucleare, si pensa in genere a uno scontro fra Stati Uniti e Unione Sovietica, in quanto solo questi due paesi dispongono dei mezzi per affrontare un simile impegno bellico. Un eventuale conflitto fra una potenza che possegga un nutrito arsenale nucleare e un paese fornito esclusivamente o quasi di armi convenzionali si risolverebbe in seguito alla minaccia dell'uso di armi nucleari o a un loro effettivo, ma limitato, impiego. Per quanto riguarda Stati Uniti e Unione Sovietica, si è parlato di almeno tre livelli di guerra nucleare: il primo, che prevede l'uso massiccio, sul campo di battaglia (da pensarsi situato lungo il confine tra i paesi appartenenti alla NATO e quelli del Patto di Varsavia), di ‛piccole' armi tattiche aventi una forza esplosiva compresa fra poche decine di chilotoni e un chilotone, o anche meno, dirette contro le forze nemiche convenzionali; il secondo, di attacco ‛limitato', da effettuarsi presumibilmente con vettori a lungo raggio, diretto esclusivamente contro le basi strategiche avversarie; e infine il terzo, di attacco ‛totale', nel corso del quale armi di potenza opportuna sarebbero dirette contro bersagli industriali e urbani, oltre che contro bersagli militari. Si è congetturato, almeno da parte di autori statunitensi, che questi livelli potrebbero rimanere separati, cioè che le ostilità potrebbero cessare a uno di questi livelli, prima che si passi al successivo (d'altra parte non si può escludere che le ostilità si manifestino direttamente con un attacco totale).

Ci si potrebbe figurare, nel caso di una guerra nucleare condotta sul campo di battaglia, una zona mobile di combattimento di ampiezza compresa tra i 10 e i 20 km. Nel caso di truppe impegnate a distanza ravvicinata, le armi più adatte sembrano quelle da un chilotone. Per un'arma del genere i raggi delle zone pericolose (per l'onda d'urto, gli effetti termici e le radiazioni) sarebbero di circa 0,5, 0,3 e i km rispettivamente. Si noti che con forze esplosive di questa entità la zona pericolosa per le radiazioni è la più estesa. Le distanze riportate si riferiscono ad aree molto pericolose per persone sprovviste di riparo o di adeguate protezioni, mentre, perché un carro armato, per esempio, possa essere messo fuori uso dall'onda d'urto, è necessario che si trovi molto più vicino alla zona dell'esplosione, anche se probabilmente il suo equipaggio verrebbe già annientato dalle radiazioni a una distanza maggiore.

Nel caso della cosiddetta ‛bomba al neutrone', i rapporti fra i tre fattori (onda d'urto, effetti termici e radiazioni) sono alterati. Questa nuova arma, infatti, emette un numero di neutroni considerevolmente maggiore dell'ordigno a fissione di potenza corrispondente, sicché, a parità di forza esplosiva, la zona pericolosa per le radiazioni risulta notevolmente più vasta. Dal momento che le radiazioni non danneggiano le strutture e gli impianti, ma solo le persone, la bomba al neutrone è un ordigno che uccide quanto una bomba a fissione, ma distrugge molto di meno. D'altra parte una bomba al neutrone dotata dello stesso potenziale distruttivo di una bomba a fissione è molto più letale.

Nel caso di attacco ‛limitato' contro la forza strategica dell'avversario, l'effetto immediato contro la popolazione civile potrebbe non essere di grande entità. Tuttavia in questa circostanza gli effetti delle radiazioni residue, dovute al fal/out ravvicinato (entro un raggio di poche centinaia di chilometri) potrebbero essere disastrosi. La possibile natura di questi effetti sarà discussa nel cap. 4.

Le conseguenze di un attacco ‛totale' contro bersagli urbani e industriali vanno di gran lunga al di là di ogni possibile previsione. Stime diverse delle perdite immediate negli Stati Uniti, fatte sulla base di vari parametri, come l'ampiezza delle zone danneggiate, il numero di bombe impiegate, il numero e la densità di popolazione dei centri colpiti, danno cifre superiori ai 100 milioni di vittime su una popolazione di poco più di 200 milioni di persone. Queste stime, peraltro, non tengono in considerazione importanti fattori secondari, come l'interruzione delle attività produttive e dei servizi, primo fra tutti l'erogazione di energia elettrica, da cui dipende la sopravvivenza della società americana. Paradossalmente una società meno ‛civilizzata' potrebbe sostenere relativamente meglio l'urto di un attacco nucleare.

È opinione diffusa che una guerra nucleare vera e propria sarebbe di breve durata. La produzione di armi nucleari, viceversa, richiede parecchio tempo, giacché un reattore da 1.000 Megawatt non produce più di 1 kg di plutonio al giorno e una sola bomba ne contiene parecchi chilogrammi. Inoltre occorre molto tempo per produrre i missili e gli altri vettori a lungo raggio. Di conseguenza una guerra nucleare può essere condotta solo con i mezzi già a disposizione, contrariamente a quanto avveniva in passato, quando le guerre, compresa la seconda guerra mondiale, venivano combattute con armi prodotte dopo l'inizio delle ostilità. Pertanto una nazione che preveda la possibilità di dover far ricorso alle armi nucleari è costretta ad allestire in tempo di pace un arsenale adeguato a tutte le evenienze. Inoltre, dato il continuo progresso tecnologico, è necessario aggiornare periodicamente interi settori dell'arsenale (come si è fatto, per esempio, introducendo i MIRV). Ciò spiega il progressivo aumento degli stanziamenti militari da parte di tutte le grandi potenze dall'avvento delle armi nucleari.

2. I fondamenti scientifici delle armi nucleari.

Durante i quarant'anni successivi alla scoperta della radioattività da parte di Becquerel (1896), si sono fatti immensi progressi nella conoscenza della struttura dell'atomo. In seguito alla scoperta del nucleo atomico è sorto un nuovo campo di ricerca, la fisica nucleare; le più importanti tappe che hanno caratterizzato lo sviluppo di questa nuova branca della scienza sono state: la constatazione che l'energia emessa in determinati processi radioattivi era milioni di volte più grande di quella ottenuta attraverso processi chimici; la conclusione di Einstein (Germania, 1905) che massa ed energia erano equivalenti (E = m c²) la scoperta delle serie radioattive naturali derivanti dagli elementi pesanti uranio e torio; la dimostrazione di Rutherford (Inghilterra, 1919) che le serie radioattive potevano essere prodotte artificialmente; la scoperta del neutrone da parte di Chadwick (Inghilterra, 1932); la scoperta, fatta da Urey (Stati Uniti, 1932), del deuterio, l'isotopo pesante dell'idrogeno che si trova in natura; le osservazioni di Fermi sulla trasformazione degli elementi e la creazione di nuovi isotopi come risultato dell'esposizione ai neutroni (Italia, 1934); l'ipotesi di Gamow e altri che le reazioni termonucleari tra elementi leggeri - nelle quali i nuclei si fondono e formano un nucleo che, sebbene più pesante, ha una massa più piccola della somma delle masse dei reagenti - fossero la probabile fonte di energia del Sole e delle stelle; e infine il riconoscimento che se si fosse spezzato in due parti approssimativamente uguali un nucleo pesante, come quello dell'uranio, sarebbe stata liberata una grande quantità di energia (forse 100 milioni di volte maggiore di quella di una singola reazione chimica).

Questa era la situazione quando O. Hahn e F. Strassmann resero nota la loro scoperta (Germania, 1938) che nel corso del bombardamento di uranio effettuato con neutroni veniva prodotto bario (un elemento la cui massa atomica è poco più della metà di quella dell'uranio). L. Meitner e O. R. Frisch, che allora lavoravano presso l'Istituto Niels Bohr di Copenhagen, avanzarono l'ipotesi che una parte dei neutroni provocasse la spaccatura, o ‛fissione', dei nuclei di uranio; immediatamente si misero al lavoro per verificare tale ipotesi. Bohr, appena arrivato negli Stati Uniti, circa a metà gennaio del 1939, comunicò quest'idea a Fermi e ad altri e prima della metà di febbraio la conferma sperimentale della fissione dell'uranio ad opera dei neutroni era stata ottenuta in una mezza dozzina di laboratori: prima a Copenhagen e subito dopo a Parigi, da parte di I. Curie e Fr. Joliot, e in quattro laboratori americani.

Fermi si era reso conto, e probabilmente non era il solo, che in concomitanza con il processo di fissione potevano essere emessi dei neutroni; infatti negli isotopi noti che hanno massa pari a circa la metà di quella dell'uranio il rapporto fra neutroni e protoni nel nucleo è sempre minore che nell'uranio, il quale, se fissionato, dà appunto luogo a tali isotopi. Nel giro di pochi mesi da parecchi laboratori venne la conferma che in concomitanza con la fissione venivano emessi neutroni e che il numero medio di neutroni prodotti era compreso tra uno e tre. Si chiarì anche che la maggior parte dei fenomeni di fissione si verificava nell'isotopo raro dell'uranio di massa 235, il quale è presente nell'uranio naturale fino a un massimo di una parte su 140, mentre il rimanente ha essenzialmente numero di massa 238. Presto ci si rese conto che una parte dei neutroni di moderata o bassa energia liberati, pur non essendo in grado di provocare la fissione, sarebbe stata assorbita o ‛catturata' e avrebbe prodotto l'isotopo ²³⁹U. Sulla base di quanto si era già osservato circa il comportamento dei nuclei pesanti, ci si aspettava che l'²³⁹U sarebbe decaduto nel ²³⁹Pu attraverso due successive emissioni beta e che il ²³⁹Pu sarebbe stato sufficientemente stabile e fissionabile quanto l'235U. Si era così giunti alla convinzione che, se si fossero potuti separare gli isotopi dell'uranio in modo da ottenere ²³⁵U abbastanza puro o se si fosse potuto produrre ²³⁹Pu in quantità sufficienti, si sarebbe realizzata una reazione a catena esplosiva. Mentre una tale possibilità era ovvia in linea di principio, fino alla metà del 1940 non si seppe se si sarebbe potuta attuare effettivamente. Troppi erano i dati e le informazioni mancanti: fra l'altro non si sapeva quanto materiale fissile sarebbe stato necessario perché si verificasse una reazione a catena, nè come produrlo in quantità sufficiente; non si sapeva nemmeno se la reazione a catena, una volta ottenuta, sarebbe stata abbastanza rapida da provocare una rilevante esplosione.

Fino a questo punto i risultati degli studi teorici e sperimentali, nonché le ipotesi sulle possibili implicazioni delle conoscenze che si stavano acquisendo, erano stati discussi secondo il tradizionale costume della ricerca scientifica accademica e tutti i ricercatori interessati all'argomento erano al corrente di tutti gli sviluppi. Le ricerche venivano portate avanti contemporaneamente in molti paesi: Gran Bretagna, Germania, Francia, Unione Sovietica e, naturalmente, Stati Uniti. Verso la metà del 1940 i principali scienziati americani e inglesi si trovarono d'accordo sul fatto che le nuove scoperte avevano implicazioni allarmanti; decisero pertanto di interrompere le pubblicazioni dei nuovi risultati più importanti. La cosa attirò ben presto l'attenzione dei fisici sovietici, per il fatto che il lavoro di G. N. Flërov e K. A. Petržak sulla fissione spontanea dell'isotopo ²³⁸U, benché pubblicato sull' ‟American physical review", non aveva ricevuto alcun commento. In Unione Sovietica l'argomento della fissione dell'uranio fu discusso apertamente per l'ultima volta (fu poi ripreso molto dopo la seconda guerra mondiale) in un congresso tenuto a Mosca nel novembre del 1940. Circa in quel periodo I. V. Kurčatov, direttore del principale laboratorio di ricerche sull'uranio, propose alle autorità sovietiche di intensificare l'attività di ricerca al fine di ottenere una reazione nucleare a catena. La proposta di Kurčatov non si potè attuare immediatamente a causa dell'invasione tedesca (giugno 1941); tuttavia già agli inizi del 1943 prese il via in Unione Sovietica un intenso programma di ricerca sulla fissione dell'uranio.

Fin dall'autunno del 1939 gli scienziati americani avevano informato i responsabili del governo delle possibili applicazioni della fissione nucleare. Tuttavia si dovette aspettare la fine del 1941 perché fosse varato un progetto di ricerca teso allo specifico scopo di realizzare la prima bomba atomica. Nel frattempo gli scienziati si erano dedicati a un lavoro puramente scientifico: avevano raccolto un gran numero di dati e di informazioni sul processo della fissione, avevano perfezionato le misure di importanti grandezze e avevano isolato minuscoli campioni di plutonio. Nell'estate del 1945, con il collaudo della prima bomba atomica, divenne drammaticamente chiaro che le primitive preoccupazioni per le terribili possibilità offerte dalla fissione nucleare erano pienamente giustificate.

Dal 1945 sono state ottenute molte informazioni su argomenti che nel 1941 erano quasi sconosciuti, fra cui i dati precisi a proposito della massa critica dell'²³⁵U praticamente puro e del ²³⁹Pu. Per definizione la massa critica di un materiale fissile è quella quantità per cui, date certe condizioni di densità e di purezza, il numero dei neutroni prodotti dalla fissione eguaglia esattamente quello dei neutroni perduti o per fuga dalla superficie o per assorbimento, senza produzione di fissione, nei materiali presenti. Il termine ‛massa critica' si riferisce a una situazione in cui non c'è alcuno strato riflettente intorno al materiale fissile o nocciolo (core). Per l'²³⁵U metallico, in condizioni normali di densità e in configurazione sferica (che è la più favorevole, giacché ha il più piccolo rapporto superficie/volume), la massa critica è di circa 50 kg e per il ²³⁹Pu di 10 kg. Quando c'è uno strato riflettente, la massa critica risulta più piccola, dato che alcuni neutroni, che altrimenti sfuggirebbero, ritornano al nocciolo. Con uno strato abbastanza spesso di un buon materiale riflettente la massa critica può essere ridotta di un fattore 2 o anche un po' di più.

Dalla definizione di massa critica appare evidente che il raggio di un nocciolo sferico nella condizione critica deve trovarsi in un determinato rapporto con il cammino libero medio di un neutrone, dato che sarà questo parametro a determinare la probabilità relativa che il neutrone ha di sfuggire dal nocciolo o di entrare in collisione con esso e provocare una fissione. Se la densità del materiale fosse aumentata di un fattore x, anche il numero dei nuclei per unità di volume sarebbe moltiplicato per x, il cammino libero medio risulterebbe x volte più corto, il raggio critico sarebbe anch'esso x volte più corto, il volume critico sarebbe ridotto di un fattore x³ e pertanto la massa critica sarebbe ridotta di un fattore pari a x² ; cioè, se la densità fosse raddoppiata, la massa critica risulterebbe ridotta a un quarto del suo valore. Su queste considerazioni si fonda il metodo di innesco di un'esplosione a fissione detto ‛di implosione', in base al quale una determinata quantità di materiale fissile, subcritica in condizioni normali, viene circondata con uno strato di esplosivo ad alto potenziale; quando questo esplosivo viene fatto esplodere, esercita una grande pressione sul materiale fissile e lo comprime a tal punto che, per la maggiore densità raggiunta, la quantità presente risulta maggiore della massa critica ed è quindi in grado di esplodere. Un metodo più ovvio e più semplice per ottenere un insieme supercritico, cioè in grado di esplodere, consiste nel far collidere, in un tempo brevissimo, due porzioni separate di materiale fissile, ciascuna di massa maggiore della metà della massa critica. Per raggiungere questo scopo si può utilizzare una delle due porzioni di materiale fissile come fosse un proiettile da fucile sparandola contro o dentro l'altra.

Il tempo necessario per giungere all'esplosione dall'inizio di una reazione a catena di neutroni in un insieme supercritico è molto breve. La velocità tipica dei neutroni emessi durante la fissione ha valori compresi fra 1 e 2 volte 10⁹ cm/s. La distanza standard percorsa da un neutrone nel materiale fissile prima di provocare un processo di fissione è di circa 10-15 cm. In media nel corso della fissione dell'²³⁵U sono emessi 2,5 neutroni (3 nel caso del ²³⁹Pu). Ciò significa che un neutrone può essere rimpiazzato da 2,5 o 3 neutroni in un tempo di circa 10^-8 s. Se questo processo viene reiterato per circa 40 volte (o poco più), la densità di energia risultante dai processi di fissione - e quindi la pressione - supererà di molto quella prodotta dall'implosione dell'esplosivo di innesco, cosicché il materiale si disperderà e l'esplosione avrà termine. L'intero processo avviene in circa mezzo microsecondo (40 × 10^-8 s). Con il metodo dello sparo è difficile ottenere una velocità del proiettile superiore a 10⁵ cm/s; la distanza che il proiettile deve percorrere tra il momento in cui le due porzioni di materiale fissile cominciano a diventare critiche e quello in cui esse sono completamente congiunte è probabile che sia di 10 cm o più, cioè dell'ordine del diametro di una massa critica. Quindi il materiale rimane supercritico per un tempo di un centinaio o di alcune centinaia di microsecondi prima che il congiungimento sia completo. Se una reazione a catena cominciasse all'inizio della collisione, il materiale esploderebbe molto prima di aver raggiunto la configurazione voluta e l'esplosione sarebbe relativamente debole. Considerazioni analoghe valgono per l'innesco ottenuto col metodo di implosione, a parte il fatto che la velocità dell'onda di compressione può essere 10 o più volte superiore e la distanza da percorrere è più breve (corrisponde al raggio anziché al diametro del nocciolo); in tal caso il tempo durante il quale il materiale risulta supercritico si aggira intorno ai 10 microsecondi o anche meno. Nell'uranio si verifica anche qualche processo di fissione spontanea, ma la sorgente di neutroni così ottenuta è talmente debole che vi sono scarse possibilità che si inizi prematuramente una reazione a catena, anche durante il periodo supercritico caratteristico del metodo dello sparo. Nel caso del plutonio, invece, anche se l'isotopo ²³⁸Pu ha un basso indice di fissione spontanea, la sorgente di neutroni risulta sempre molto intensa, a causa dell'inevitabile presenza di una piccola percentuale dell'isotopo ²⁴⁰Pu, che ha un indice di fissione spontanea molto elevato. Per via di questo fatto il plutonio non può essere utilizzato quando si applica il metodo dello sparo, perché si avrebbe certamente un'esplosione prematura durante il processo di congiungimento. Anche ricorrendo al metodo di implosione, se si usa il plutonio, non si può trascurare la possibilità, per quanto piccola, che si verifichi un'esplosione prematura. L'²³⁵U può essere usato sia adottando il metodo dello sparo sia quello di implosione; in questo caso, data la compressione del materiale, si può ottenere l'esplosione anche con una massa più piccola.

Tutte queste informazioni riguardano sostanzialmente i primitivi modelli di armi nucleari, le cui caratteristiche sono state rese pubbliche; i dettagli tecnici delle armi termonucleari, invece, sono tuttora mantenuti segreti.

3. Alcune caratteristiche particolari delle armi nucleari.

L'importanza tattica dell'altissimo rapporto forza esplosiva-peso delle armi nucleari è già stata discussa. Un'altra conseguenza dell'alto valore di questo rapporto è che, al momento dell'esplosione, il materiale di cui è fatta la bomba raggiunge una temperatura estremamente elevata: più di un milione di gradi centigradi nelle prime armi nucleari e più di 10 milioni in quelle successive, per le quali il rapporto in questione può essere anche di 1 chilotone/kg. Naturalmente i frammenti della bomba si disperdono e si raffreddano molto rapidamente; ma finché sono caldi (a una temperatura che può essere di 2.000 °C) irradiano energia a un ritmo estremamente rapido sotto forma di raggi X, o fotoni, che hanno uno spettro caratteristico della temperatura del materiale.

Se l'esplosione si verifica in condizioni di vuoto quasi assoluto (per esempio a grandissime altitudini), questi raggi X termici raggiungono grandi distanze dal punto dell'esplosione surriscaldando ed eventualmente distruggendo qualsiasi corpo incontrino (un satellite o un missile a testata esplosiva). Al livello del mare questi raggi X vengono assorbiti in uno strato d'aria molto sottile, che si riscalda fino al punto di irradiare a sua volta energia, formando in tal modo un volume crescente di aria molto calda, la cui temperatura diminuisce progressivamente con l'aumentare del volume stesso. Quando la temperatura scende al di sotto dei 10.000 °C, lo spettro dei fotoni irradiati si sovrappone alla gamma del visibile, cioè all'intervallo di lunghezze d'onda per cui l'aria risulta trasparente, cosicché gran parte dell'energia irradiata può propagarsi fino a grandi distanze dal punto dell'esplosione.

Una volta che la temperatura sia scesa a 2.000 °C, il fungo atomico smette, praticamente, di irradiare energia, perché l'efficienza di questo processo diminuisce con la quarta potenza della temperatura. Tuttavia, nell'intervallo di tempo impiegato dalla temperatura a scendere da 10.000 a 2.000 OC, circa un terzo dell'energia dell'esplosione lascia il fungo atomico sotto forma di radiazione termica. Questa è l'origine degli effetti incendiari provocati dalle armi nucleari. Gli effetti termici sono invece insignificanti nel caso degli esplosivi chimici, dato che la temperatura in questo caso si aggira intorno ai 3.000 °C soltanto e solo una piccola energia viene irradiata.

Un'altra conseguenza del fatto che una grande massa d'aria raggiunga temperature superiori ai 2.000 °C (circa mille tonnellate d'aria per ogni chilotone di forza esplosiva) è che a temperature così elevate una piccola frazione d'aria viene convertita in ossido di azoto (NO) e quando l'aria si raffredda al di sotto dei 2.000 °C il processo di riconversione dell'ossido di azoto diventa tanto lento che la sua concentrazione si stabilizza intorno all'1% (circa 5 tonnellate per chilotone). La molecola di NO reagisce con l'ozono e, se fosse trasportata nella stratosfera, come accadrebbe nel caso di esplosioni dell'ordine di grandezza dei megatoni, esaurirebbe lo strato di ozono che protegge la Terra dai raggi ultravioletti provenienti dal Sole. Naturalmente per alterare in maniera sensibile la quantità di ozono presente nella stratosfera dovrebbero verificarsi esplosioni della forza di parecchi megatoni; tuttavia questa eventualità fa parte delle possibili conseguenze di una guerra nucleare totale, come vedremo nel cap. 4.

Un'altra importante caratteristica delle esplosioni nucleari è la produzione di radiazione, sotto forma di neutroni, raggi gamma (o raggi X) e raggi beta. Per convenienza questa radiazione può essere suddivisa in radiazione istantanea - che è sostanzialmente emessa al momento dell'esplosione e che danneggia le persone vicine ed esposte al momento dello scoppio - e radiazione residua - che viene principalmente emessa dai frammenti della fissione; quest'ultima diminuisce di intensità abbastanza rapidamente, ma può risultare pericolosa per giorni o per anni, sia in forma di ricaduta di particelle di materiale radioattivo (fallout 'vicino' o ‛locale', che si verifica approssimativamente entro le prime 24 ore), sia in forma di fallout a lungo raggio, su scala mondiale.

Alcuni effetti delle radiazioni istantanee sono già stati descritti; ve ne possono essere altri. I raggi gamma, urtando gli elettroni presenti nell'aria, li allontanano dalla zona dell'esplosione; si viene così a formare una guaina di corrente che molto probabilmente non ha simmetria sferica. Questo fenomeno può generare un forte impulso elettromagnetico, che provoca gravi danni nei circuiti elettronici e nelle linee telefoniche, telegrafiche e di trasmissione, a meno che questi apparati non siano stati adeguatamente schermati. Ad altitudini elevate la radiazione istantanea crea una vasta nube di aria ionizzata, in grado di interrompere, per un breve periodo, le comunicazioni radar; questo stesso tipo di radiazione, in concomitanza con la radiazione residua, può causare uno stato anomalo di ionizzazione e provocare di conseguenza, entro una zona piuttosto estesa, l'interruzione delle comunicazioni radio a lunga distanza. Inoltre i neutroni e i raggi gamma della radiazione istantanea possono, come la radiazione termica di cui si è già parlato, danneggiare i satelliti artificiali e le testate nucleari dei missili vettori.

Per quel che riguarda la radiazione residua è opportuno distinguere due casi: il caso di un'esplosione in quota e quello di un'esplosione in superficie o vicino alla superficie. Per esplosione in quota si intende un'esplosione in cui il fungo atomico non tocca terra. In questo caso la nube atomica non trasporta, praticamente, altro materiale solido oltre a quello che costituisce l'ordigno, che è piuttosto poco. Di conseguenza le particelle solide che si formano per condensazione a mano a mano che la nube si raffredda sono piccolissime e ricadono sulla Terra molto lentamente (alcune possono anche impiegare giorni o anni a ricadere sulla superficie terrestre). Questo materiale, quindi, una volta ritornato sulla superficie terrestre sarà largamente diffuso e contribuirà al livello generale di fondo della radiazione in minima parte.

Nel caso di un'esplosione in superficie o vicino alla superficie un'enorme quantità di materiale viene sollevata e incorporata nella nube atomica, con la conseguenza che si formano particelle di condensazione più grandi che ricadono più rapidamente a terra. Circa la metà del materiale radioattivo proveniente dai detriti dell'ordigno può ricadere sulla superficie terrestre entro le prime 24 ore dall'esplosione. In presenza di un vento costante a 15 nodi gran parte di questi detriti si deposita entro un raggio di circa 600 km; i detriti residui si diffondono come nel caso di un'esplosione in quota.

La forma e l'estensione dell'area entro cui l'esposizione alle radiazioni di fallout può essere rischiosa o addirittura fatale dipendono, oltre che dalla forza esplosiva dell'arma, anche dalla velocità e dalla variabilità del vento, dalla possibilità che le precipitazioni aumentino il fallout in particolari località e da altri fattori. Comunque si può dire che, nel caso di un'esplosione in superficie da 1 megatone, in presenza di un vento costante a 15 nodi, l'esposizione alle radiazioni nelle 24 ore successive all'esplosione potrebbe riuscire letale a una persona che rimanesse, senza riparo, entro un'area approssimativamente rettangolare di circa 10 x 70 km, con il lato corto intersecante il punto dell'esplosione e il lato lungo parallelo alla direzione del vento (ovviamente sottovento). Entro un'area un po' più ampia - di 15 x 100 km - l'esposizione alle radiazioni, per quanto molto dannosa, non risulterebbe, di norma, letale. Un buon riparo riduce considerevolmente il danno provocato dalle radiazioni: già una casa ben costruita lo ridurrebbe di un fattore 3 circa.

Gli effetti del fallout, pur non essendo micidiali come gli effetti diretti dell'esplosione, possono essere gravissimi anche a grandi distanze. Se poi si verificasse un bombardamento intensivo effettuato con parecchi ordigni nucleari fatti esplodere entro una zona relativamente ristretta, le aree di fallout si sovrapporrebbero e i relativi effetti si sommerebbero. Un caso limite di questo genere si verificherebbe se venisse attaccata una delle basi di ICBM ‛Minuteman' in dotazione agli Stati Uniti. Queste installazioni, infatti, si estendono per un centinaio di chilometri e contengono 150 o 200 missili dislocati a distanza tale gli uni dagli altri che per distruggerli è necessario colpirli individualmente. Inoltre essi sono così ben protetti nei loro silos sotterranei che anche l'esplosione di un ordigno da un megatone dovrebbe avvenire a meno di un chilometro dal bersaglio per garantirne la distruzione. Per effettuare un attacco veramente efficace sarebbe probabilmente opportuno lanciare almeno due bombe contro ogni missile. Un bombardamento nucleare di una base del genere, quindi, implicherebbe l'esplosione di parecchie centinaia di ordigni da un megatone, probabilmente in superficie o vicino alla superficie, entro un'area limitata. La zona spazzata dalle radiazioni sarebbe molto estesa; in caso di vento favorevole potrebbe allungarsi ben oltre i 1.000 km e raggiungere regioni densamente popolate.

4. Effetti di una guerra nucleare totale.

In questo capitolo saranno illustrati i probabili effetti su scala mondiale di una guerra nucleare totale fra Stati Uniti e Unione Sovietica. Delle conseguenze di una simile eventualità sui paesi belligeranti abbiamo già parlato. Pur supponendo che gli obbiettivi attaccati si trovino solo in territorio americano e sovietico, è chiaro che anche altri paesi, soprattutto nell'emisfero settentrionale, rimarrebbero danneggiati dagli attacchi nucleari.

Gli effetti fisici più ovvi, a lungo raggio, derivanti direttamente dalle esplosioni dovrebbero essere quelli causati dal fallout, dalla polvere in sospensione nell'atmosfera e dall'impoverimento dello strato di ozono provocato dalle grandi quantità di NO trasportate nella stratosfera.

A distanze superiori a un migliaio di chilometri dai paesi bombardati il fallout si distribuirebbe piuttosto uniformemente su tutto il resto dell'emisfero settentrionale e in parte, circa un terzo, anche su quello meridionale. Su questo punto si è già in possesso di dati sperimentali ricavati dalle prove atmosferiche condotte soprattutto dagli Stati Uniti e dall'Unione Sovietica, nel corso delle quali sono stati prodotti circa 200 megatoni di forza esplosiva da fissione. Secondo le stime del SIPRI la capacità totale di lancio di Stati Uniti e Unione Sovietica è prossima ai 15.000 megatoni, dei quali circa 8.000 sarebbero prodotti per fissione. Se tutte queste armi esplodessero, la quantità di radioattività residua immessa nell'atmosfera sarebbe circa 40 volte superiore a quella immessavi nel corso delle esplosioni di prova. Facendo le proporzioni con le conclusioni raggiunte dall'United Nations Scientific Committee on the Effects of Atomic Radiation (UNSCEAR) a proposito degli effetti delle radiazioni generate dagli esperimenti nucleari, si può calcolare che nei 30-40 anni successivi all'esplosione di ordigni a fissione per un totale di 8.000 megatoni gli abitanti dell'emisfero settentrionale sarebbero esposti a un quantitativo di radiazioni circa doppio rispetto a quello dovuto alla naturale radiazione di fondo. Considerando il fatto che già molti milioni di persone vivono in zone montuose dove la radiazione naturale di fondo è doppia e anche tripla rispetto a quella presente a livello del mare e che ciò non pare comporti conseguenze rilevanti, si potrebbe concludere che l'aumento delle radiazioni dovuto a una guerra nucleare non produrrebbe gravi effetti sulla totalità della popolazione. In particolare si ritiene che tali radiazioni addizionali causerebbero un aumento del numero di decessi per tumore di appena il 4% circa e un aumento analogo, se non addirittura minore, dell'incidenza di difetti genetici significativi.

La quantità di polvere lanciata negli strati superiori dell'atmosfera sarebbe molto grande (parecchie decine di milioni di tonnellate), ma non molto superiore a quella espulsa nell'eruzione del Krakatoa del 1883, che provocò un abbassamento della temperatura media sulla superficie terrestre di pochi decimi di grado centigrado per circa un anno: una variazione del genere rientra nelle normali variazioni climatiche.

È probabile che solamente esplosioni con forza superiore a un megatone potrebbero trasportare l'NO così in alto da interagire con lo strato di ozono. La tendenza cui già si è accennato, di sostituire grosse testate termonucleari con MIRV di potenza assai inferiore, ridurrebbe le scorie, che verrebbero poi immesse nella stratosfera. Tuttavia, nel caso di molte esplosioni da molti megatoni, la quantità di NO immessa nella stratosfera potrebbe superare di varie volte la quantità normalmente presente, riducendo così lo strato di ozono nell'emisfero settentrionale. Per tutto il periodo (di 5 o 10 anni) in cui la riduzione si mantenesse significativa, si avrebbe un aumento della radiazione ultravioletta che raggiunge la superficie terrestre. Ciò porterebbe a un aumento del 10% circa dei casi di tumore della pelle, di ustione solare grave e di accecamento dovuto al riverbero sulla neve, a meno che non venissero prese speciali precauzioni. Potrebbe anche verificarsi un cambiamento nella distribuzione del riscaldamento della stratosfera, che si ripercuoterebbe sugli spostamenti d'aria alle quote sottostanti e che potrebbe portare a qualche variazione climatica.Tutti questi processi, però, non sono ancora ben compresi e pertanto non se ne possono prevedere con sicurezza gli effetti; si ritiene tuttavia che tali fenomeni non possano provocare mutamenti che eccedano i limiti della normale variabilità. In effetti pare che le conseguenze più gravi di una guerra nucleare totale per i paesi non coinvolti direttamente deriverebbero da altri fattori. Si pensi, per esempio, che gli Stati Uniti, attualmente, esportano enormi quantità di generi alimentari essenziali; malgrado ciò molte popolazioni rischiano la morte per inedia. Nel caso gli Stati Uniti fossero devastati da una guerra nucleare, potrebbero i sopravissuti, demoralizzati e privati di ogni mezzo di produzione, provvedere, oltre che alle proprie necessità, anche a quelle dei paesi da essi dipendenti?

Bibliografia.

Glasstone, S., The effects of nuclear weapons, Washington 1964.

Golovin, I. N., I.V. Kurchatov, Bloomington 1968.

SIPRI (Stockholm International Peace Research Institute), World armaments and disarmament. Yearbook 1978, London 1978.

Smyth, H.D., Atomic energy for military purposes, Princeton 1945.

UNSCEAR (United Nations Scientific Committee on the Effect of Atomic Radiation), Ionizing radiation levels and effects, New York 1972.

U.S. National Academy of Sciences, Long-term worldwide effects of multiple nuclear-weapons detonations, Washington 1975.