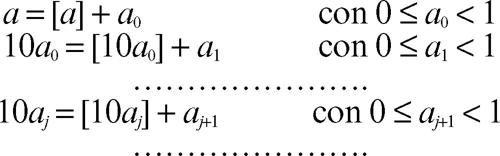numerazione

numerazione

numerazione metodo per esprimere numeri mediante simboli. Il sistema di numerazione si dice additivo se ogni simbolo denota sempre la stessa quantità (come per esempio nel → sistema di numerazione romano), si dice invece posizionale (→ sistema di numerazione posizionale) se la posizione di un simbolo è significativa della quantità da esso espressa (come per esempio nell’ordinario sistema decimale dove, da destra verso sinistra, la cifra in prima posizione, prima dell’eventuale virgola, indica le unità, la seconda le decine ecc.). Il sistema di numerazione di uso universale è quello posizionale decimale (→ sistema decimale), tuttavia per scopi specifici si utilizzano anche altri sistemi posizionali, come quello binario, ottale, o esadecimale.

Un numero naturale si rappresenta mediante un allineamento di cifre c_k c_k−1 ... c₀, che rappresenta una combinazione di potenze non negative di 10, precisamente c_k10^k + ... + c₀10⁰. Per un numero razionale non negativo, espresso sotto forma di frazione ridotta a /b, si ricava la rappresentazione decimale eseguendo dapprima la divisione con resto, a = nb + r₀, dove 0 ≤ r₀ < b, che fornisce la parte intera del numero, e quindi successive divisioni

che forniscono le cifre della parte decimale, c₋₁, c₋₂, ... La rappresentazione è costituita da un numero finito di cifre se e solo se il denominatore b è divisore di una qualche potenza intera positiva di 10. Il numero delle cifre c_−i, dette cifre decimali, è uguale all’esponente della più piccola potenza dotata di questa proprietà, e si parla di numero decimale limitato e si scrive a /b = n, c₋₁ c₋₂ ... c_−r; questa notazione significa che a /b = n + c₋₁/10 + ... + c_−r /10^r. In ogni altro caso si parla di numero decimale illimitato (in particolare, di → numero periodico).

Un numero irrazionale è caratterizzato da un allineamento di cifre decimali illimitato non periodico. In generale, lo sviluppo decimale di un numero reale a positivo si ottiene nel modo seguente: indicando con [a] la parte intera di a (ossia il più grande intero che non supera a) si ha

e quindi, posto n = [a] e c_−j = 10a_j−1, si ottiene lo sviluppo: a = n,c₋₁ c₋₂ ... Escludendo gli sviluppi periodici con periodo 9, la corrispondenza tra numeri reali e sviluppi decimali è biunivoca. Le considerazioni precedenti si estendono al caso generale di numerazione b-esimale in una base b ≥ 2 qualsiasi, con b intero (→ sistema di numerazione posizionale).