numero primo

numero primo

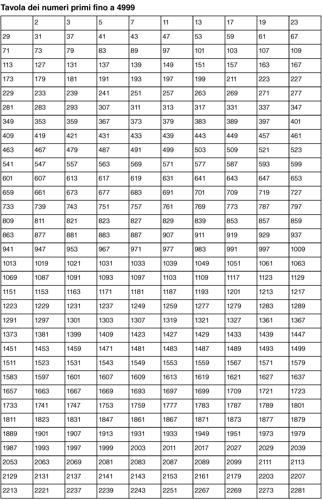
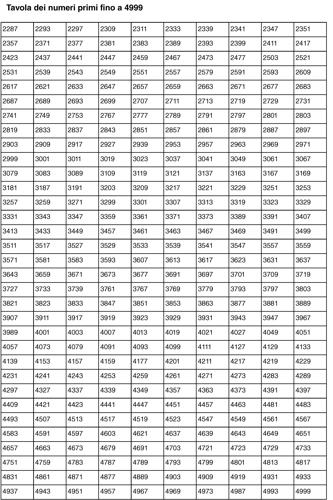
numero primo numero intero maggiore di 1 che ammette solo divisori banali, cioè 1 e sé stesso. Questa proprietà, che nell’ambito dei numeri interi coincide con quella di primalità, va più in generale sotto il nome di irriducibilità. In modo equivalente si può definire numero primo un numero intero maggiore di 1 che ogniqualvolta divide un prodotto a ⋅ b allora divide almeno uno dei due fattori. Un numero intero che non è primo si dice composto. I numeri primi costituiscono i “mattoni fondamentali” da cui può essere ricavato ogni numero intero: ogni numero intero può in effetti essere scomposto in modo unico (a meno del segno e a meno di riordinamenti dei fattori) come prodotto di numeri primi (→ numero intero, scomposizione in fattori di un): questo fatto, che va sotto il nome di teorema fondamentale dell’aritmetica, determina sull’anello Z dei numeri interi la struttura di dominio a fattorizzazione unica. È noto sin dai tempi di Euclide che i numeri primi sono infiniti; essi formano pertanto una successione, detta successione dei numeri primi, i cui primi termini sono 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31 (si vedano le tavole dei numeri primi). Un problema classico è quello di stabilire quando una progressione aritmetica della forma a_n = r + qn contenga infiniti numeri primi: tale problema è l’oggetto del teorema di Dirichlet, il quale stabilisce che ciò avviene se e solo se r e q sono coprimi (→ Dirichlet, teorema di).

Interessante e ricco di implicazioni è il problema della distribuzione dei numeri primi, problema studiato a partire dalla fine del xviii secolo, con i lavori di C.F. Gauss e A.-M. Legendre. Importanti risultati a tale riguardo sono il teorema dei → numeri primi, che stabilisce che

dove π(n) indica il numero dei numeri primi minori di n (→ numeri primi, funzione enumerativa dei; → Eulero, funzione toziente di) e log(n) indica il logaritmo naturale di n. Fondamentale nello studio della distribuzione dei numeri primi è la funzione (di variabile complessa) detta zeta di Riemann, indicata con il simbolo ζ(s) e che, ristretta alla semiretta dei numeri reali maggiori di 1, ha la forma

Il collegamento di tale funzione con i numeri primi si fonda sulla cosiddetta identità di Eulero

dove {p_i} indica la successione dei numeri primi. A partire da tale identità, si può dimostrare che l’andamento della funzione zeta risulta legato alla distribuzione dei numeri primi; pertanto la dimostrazione dell’ipotesi di Riemann sulla distribuzione degli zeri complessi della funzione zeta avrebbe forti ripercussioni sulla distribuzione dei numeri primi (→ Eulero, prodotto di; → Riemann, funzione zeta di; → Riemann, ipotesi di).

Nell’insieme di numeri primi si possono distinguere alcune sottocategorie:

• numeri primi caudati: numeri primi tali che, tolta la cifra dell’unità, rimangono numeri primi. Tale è per esempio il numero 73, che, privo della cifra dell’unità, rimane 7, numero anch’esso primo;

• numeri primi gemelli: → numeri gemelli;

• numeri primi reversibili: numeri primi che scritti in ordine inverso nella loro rappresentazione decimale rimangono numeri primi. Sono tali per esempio 17, 71 e 31, perché anche 71, 17 e 13 sono numeri primi.

approfondimento