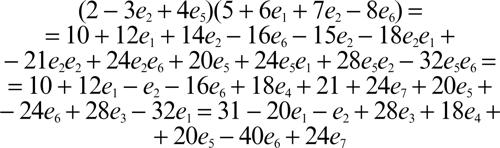O

O

O (insieme degli ottetti) detti anche ottetti di Cayley o numeri di Cayley, particolare struttura algebrica, indicata con la lettera O, inventata in maniera indipendente dal matematico irlandese J.Th. Graves e da A. Cayley, che per primo ne fece oggetto di pubblicazione nel 1845. È un’algebra non associativa e non commutativa che estende il corpo H dei → quaternioni. Gli ottetti formano un’algebra di divisione normata di dimensione 8 sul campo R dei numeri reali; più precisamente, essi sono la più grande algebra di divisione normata su R (→ Hurwitz, teorema di). Una speciale base di O come algebra su R è quella costituita dagli elementi invertibili di norma unitaria e₀, e₁, ..., e₇, dove e₀ = 1 è l’elemento neutro della moltiplicazione e dove ogni altro e_i soddisfa la relazione e_i² = −1. Insieme ai loro opposti, gli elementi di tale base sono detti le unità degli ottetti; ogni unità diversa da 1 è detta immaginaria. Un ottetto è dunque una scrittura del tipo

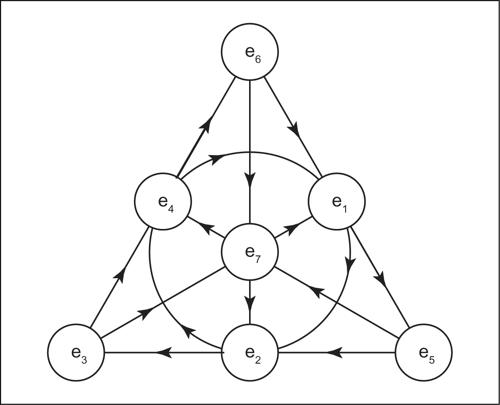
in cui ognuno degli a_i è un numero reale. Come per i numeri complessi e i quaternioni, l’insieme delle unità degli ottetti soddisfa tutti gli assiomi di gruppo tranne l’associatività: in particolare, esso è chiuso rispetto alla moltiplicazione e all’operazione di inverso. Il prodotto di due unità diverse da 1 e −1 può essere determinato identificando e₁, ..., e₇ con i sette punti del piano di Fano come mostrato in figura (→ geometria finita). Il piano di Fano, che coincide con il piano proiettivo dello spazio vettoriale tridimensionale (F₂)³ (dove il campo di definizione è il campo con due elementi F₂ per il quale si veda → Galois, campo di), è composto di sette punti e sette rette. Esso può essere rappresentato graficamente mediante un triangolo equilatero, identificando l’insieme dei punti con l’insieme i cui elementi sono i vertici del triangolo, i punti medi dei lati del triangolo e il centro del triangolo. L’insieme delle rette del piano di Fano resta in questo modo identificato con l’insieme i cui elementi sono i lati del triangolo, le mediane del triangolo e la circonferenza inscritta al triangolo; si osservi che ogni retta contiene esattamente tre punti e che per ogni coppia di punti esiste un’unica retta che li contiene. Si orientino le rette del piano di Fano e si identifichino le unità degli ottetti e₁, ..., e₇ con i punti del piano di Fano, come in figura. Allora il prodotto e_ie_j coincide con il terzo punto della retta determinata da e_i ed e_j preso con segno positivo se e_i è l’antecedente immediato di ej nell’orientamento della retta, con segno negativo altrimenti (le sei rette non chiuse vanno tutte considerate come “chiuse all’infinito”: gli “ultimi” punti di tali rette sono dunque antecedenti immediati dei “primi”). Quindi, per esempio: e₆e₁ = e₅, e₅e₁ = −e₆, e₅e₆ = e₁. L’addizione e la moltiplicazione tra ottetti si effettuano come l’addizione e la moltiplicazione tra polinomi, salvo sostituire gli opportuni prodotti tra basi. Per esempio, omettendo le basi con coefficienti nulli:

Si può notare che l’unità {1} genera una sottoalgebra di O isomorfa a R, campo dei numeri reali, le unità {1, e_i} generano sottoalgebre di O isomorfe a C, campo dei numeri complessi, per ogni i diverso da zero, e le unità {1, e_i, e_j, e_k} generano sottoalgebre isomorfe a H, corpo dei quaternioni, se e_i, e_j, e_k appartengono alla stessa retta del piano di Fano.