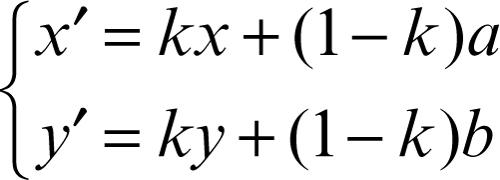omotetia

omotetia

omotetia (dal greco homós, uguale, e tithênai, porre, «di uguale posizione») in geometria, trasformazione geometrica del piano o dello spazio che, fissato un punto Z e un numero reale k ≠ 0, a ogni punto P associa il punto P′ tale che valga la relazione

Il punto Z è detto centro dell’omotetia, il numero reale k ≠ 0 è detto rapporto di omotetia. Inoltre se k > 0, i punti corrispondenti P e P′ sono dalla stessa parte rispetto al centro Z; se k < 0, i punti corrispondenti P e P′ sono invece da parti opposte rispetto al centro Z; se k = 1, si ha l’identità, se k = −1 si ha la simmetria centrale di centro Z. L’inversa di un’omotetia di centro Z e rapporto k è un’omotetia di centro Z e rapporto 1/k. Due figure che si corrispondono in un’omotetia sono dette figure omotetiche. Una omotetia ha come punto unito il centro Z e come rette unite tutte le rette per Z. Il prodotto di due omotetie di rispettivi centri Z e Z′ e rispettivi rapporti k e k′ è ancora un’omotetia di rapporto k ⋅ k′ e di centro opportuno. Nel piano cartesiano, le equazioni di una omotetia di centro Z(a, b) e rapporto k ≠ 0 sono

Sono invarianti di un’omotetia l’allineamento e la complanarità dei punti, il parallelismo, le ampiezze dei diedri e degli angoli e l’orientamento (orario o antiorario) dei punti del piano. Una omotetia, inoltre, trasforma circonferenze in circonferenze e sfere in sfere, ma non conserva le lunghezze che vengono alterate di un fattore |k|, mantenendo, quindi, il rapporto tra segmenti.

Da un punto di vista generale, un’omotetia può essere considerata una particolare → omologia. Nel piano è un’omologia avente per asse di omologia la retta impropria e per centro di omologia un punto proprio. Nello spazio è un’omologia avente per piano di omologia il piano improprio e per centro di omologia un punto proprio. Il rapporto di omotetia è dato dalla caratteristica dell’omologia. Una omotetia può essere considerata anche come:

• una particolare → similitudine nella quale risulta costante il rapporto tra le distanze dal centro dell’omotetia di due punti corrispondenti;

• una particolare trasformazione affine di uno spazio euclideo (→ affinità).

Se il centro dell’omotetia coincide con l’origine del sistema di riferimento, l’omotetia è una trasformazione lineare (prodotto di due stiramenti di uguale fattore lungo ciascuno degli assi coordinati), la cui matrice associata è la matrice diagonale avente sulla diagonale principale tutti gli elementi uguali a k. Dalla composizione di un’omotetia con una isometria si ottiene una similitudine.

Un caso particolare di omotetia può essere considerato quello in cui il centro Z non sia un punto proprio bensì un punto all’infinito α: in tal caso, a ogni punto P corrisponde un punto P′ tale che il segmento PP′ appartenga a una retta di direzione α; l’omotetia si riduce a una traslazione e il valore assoluto del rapporto di omotetia k è uguale a 1.