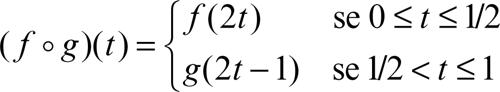omotopia

omotopia

omotopia in topologia algebrica, concetto fondamentale, da cui deriva la relazione di equivalenza sull’insieme degli spazi topologici detta equivalenza omotopica. Dal momento che spazi topologici omotopicamente equivalenti sono anche topologicamente equivalenti, il concetto di omotopia è rilevante nel fondamentale problema di stabilire se due spazi topologici sono topologicamente equivalenti oppure no.

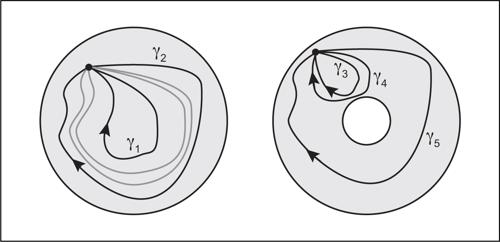
In termini intuitivi, si può pensare a un’omotopia come a una funzione ƒ₀: X → Y (tra due spazi topologici X e Y) che viene deformata nel tempo in maniera continua fino a ottenere una nuova funzione ƒ₁: X → Y. Per esempio, nella deformazione di un ciclo orientato, l’omotopia descrive la deformazione che ne mantiene il carattere di linea chiusa orientata; tale deformazione può anche radicalmente ridurlo a un punto. In un cerchio, ogni ciclo può essere così deformato, mentre in una corona circolare non tutti i cicli possono essere ridotti a un punto: è il caso di quelli che contengono al loro interno il foro della corona.

Un esempio più astratto è dato da una famiglia di funzioni F(x, t) = ƒ₀(x) + t [ƒ₁(x) − ƒ₀(x)], che è un’omotopia tra due funzioni ƒ₀ e ƒ₁ da uno spazio X in Rⁿ: F coincide con ƒ₀ all’istante t = 0 e coincide con ƒ₁ all’istante t = 1. Se le due funzioni riguardano i morfismi che definiscono due complessi di catene, si parla di omotopia di catene. La definizione formale fa uso della topologia prodotto sullo spazio topologico prodotto X × I, dove I è l’intervallo chiuso [0, 1] di R. Siano ƒ₀: X → Y e ƒ₁: X → Y due funzioni continue tra due spazi topologici X e Y e sia X × I lo spazio topologico prodotto. Un’omotopia tra ƒ₀ e ƒ₁ è un’applicazione continua F: X × I → Y tale che F(x, 0) = f₀(x) e F(x, 1) = ƒ₁(x) per ogni x in X. Se una tale omotopia esiste, ƒ₀ e ƒ₁ si dicono omotope. Risulta molto utile anche la seguente nozione più generale. Sia A un sottoinsieme di X e siano ƒ₀: X → Y e ƒ₁: X → Y due funzioni continue tali che ƒ₀(a) = ƒ₁(a) per ogni a in A. Un’omotopia relativa ad A tra ƒ₀ e ƒ₁ è un’omotopia F tra ƒ₀ e ƒ₁ tale che F(a, t) = ƒ₀(a) = ƒ₁(a) per ogni a in A e per ogni t in I. Se una tale omotopia esiste, ƒ₀ e ƒ₁ si dicono omotope relativamente ad A. Nel caso A = ∅, si ottiene la definizione di omotopia.

Due spazi topologici si dicono omotopicamente equivalenti (o dello stesso tipo di omotopia) se esistono due funzioni continue ƒ: X → Y e g: Y → X tali che le due composizioni g ∘ ƒ e ƒ ∘ g sono omotope, rispettivamente, alla funzione identità su X e alla funzione identità su Y. Uno spazio topologico si dice contraibile se è omotopicamente equivalente allo spazio topologico formato da un solo punto p. Per esempio, lo spazio Rⁿ (con topologia euclidea) è contraibile. Infatti, definendo ƒ: {p} → Rⁿ con ƒ(p) = (0, ..., 0) e g: Rⁿ → {p} nell’unico modo possibile, si ha che g ∘ ƒ coincide con l’identità su {p} mentre ƒ ∘ g è omotopa all’identità su Rⁿ (una possibile omotopia è F(x, t) = tx). La sfera (n − 1)-dimensionale Sⁿ⁻¹ e Rⁿ {(0, ..., 0)} sono omotopicamente equivalenti: l’inclusione i: Sⁿ⁻¹ → Rⁿ {(0, ..., 0)} e la funzione g: Rⁿ {(0, ..., 0)} → Sⁿ⁻¹, definita da g(x) = x/||x||, hanno le proprietà richieste poiché g ∘ i coincide con l’identità su Sⁿ⁻¹ e i ∘ g è omotopa all’identità su Rⁿ {(0, ..., 0)} (una possibile omotopia è F(x, t) = xe^{(t −1)ln(||x||)}).

Utilizzando la nozione di omotopia, si può associare a ogni spazio topologico X un gruppo le cui proprietà algebriche riflettono le proprietà topologiche di X. Tale gruppo prende il nome di gruppo fondamentale di X, o primo gruppo di omotopia (se X non è connesso per archi, tale gruppo dipende dalla scelta di un punto base x₀). Esso è un invariante omotopico, cioè se due spazi topologici sono omotopicamente equivalenti (e quindi se sono topologicamente equivalenti) hanno gruppi fondamentali isomorfi. Fissato un punto x₀ di X e denotato con I l’intervallo chiuso [0, 1] di R, un cammino o arco, di punto iniziale e punto finale x₀, è una funzione continua ƒ: I → X tale che ƒ(0) = ƒ(1) = x₀. Un tale cammino viene anche detto cappio di base x₀. Si può pensare a un oggetto che si muove sullo spazio topologico e che parte dal punto x₀ all’istante iniziale t = 0 e torna al medesimo punto all’istante finale t = 1. Due cappi di base x₀ si dicono equivalenti se sono omotopi relativamente a {0, 1}. Il gruppo fondamentale di X con punto base x₀ è il gruppo che ha come elementi le classi di equivalenza dei cappi di base x₀ e il cui prodotto è definito sui rappresentanti ƒ e g di due classi nel modo seguente:

Il prodotto è ben definito, cioè non dipende dalla scelta dei rappresentanti. Intuitivamente, il prodotto di due cammini consiste nel compiere il primo cammino a velocità tale da ritrovarsi all’istante intermedio t = 1/2 nel punto x₀ e poi compiere anche il secondo cammino con uguale velocità. Il gruppo fondamentale di X con punto base x₀ viene solitamente denotato con π₁(X, x₀). Esso coincide con il gruppo fondamentale con punto base x₀ della componente per archi di X contenente x₀ (in particolare, se X è dotato della topologia discreta, il gruppo è ridotto al solo elemento neutro). Se x₀ e x₁ appartengono alla stessa componente connessa per archi di X, π₁(X, x₀) e π₁(X, x₁) sono isomorfi. Quindi, se X è uno spazio connesso per archi, si può parlare di gruppo fondamentale di X senza specificare il punto base. Uno spazio X si dice semplicemente connesso se è connesso per archi e ha gruppo fondamentale ridotto al solo elemento neutro. Per esempio, un cerchio C è semplicemente connesso poiché è connesso per archi e, fissato un punto qualsiasi x₀, tutti i cammini in C di punto iniziale e finale x₀ sono omotopi tra loro (tutti i cicli sono riconducibili al punto iniziale) e quindi il gruppo fondamentale ha un solo elemento. Invece in una corona circolare O due cicli sono omotopi soltanto se compiono uno stesso numero n di giri, nello stesso verso, attorno al foro della corona; il gruppo fondamentale di una corona circolare O risulta isomorfo a Z: infatti, denotato con c il ciclo che gira una volta attorno al foro di O, il gruppo fondamentale è formato da tutte le potenze intere di c (se n > 0 è un numero naturale, si può percorrere il ciclo c un numero n di volte ottenendo la potenza n-esima del ciclo, oppure percorrerlo in senso contrario n volte ottenendo la potenza con esponente −n).