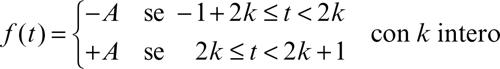onda

onda

onda nelle applicazioni della matematica alla fisica, termine che indica una vasta gamma di fenomeni aventi come caratteristica comune una propagazione di tipo oscillatorio o vibrazionale attraverso lo spazio, mediante la quale viene trasportata dell’energia. Esempi di onde sono le vibrazioni elastiche, la trasmissione del suono e le onde elettromagnetiche (luce, raggi infrarossi, onde radio ecc.). Dal punto di vista matematico, scelto un sistema di riferimento cartesiano, un’onda che si propaga lungo l’asse delle x viene descritta da una funzione delle coordinate e del tempo del tipo ƒ(x, t) = ƒ(x ± vt). Se nell’argomento compare il segno –, si parla di onda progressiva; il termine è giustificato dal fatto che, se all’istante t la funzione assume un certo valore nel punto x, trascorso un tempo Δt la funzione assume lo stesso valore nel punto x + Δx, con Δx = vΔt e pertanto il profilo dell’onda trasla in avanti con velocità v. Viceversa, se nell’argomento compare il segno +, si parla di onda regressiva che trasla all’indietro. Generalizzando al caso in cui l’onda si propaghi in una direzione arbitraria, si ottengono funzioni del tipo ƒ(x, y, z, t) = ƒ(cosαx + cosβy + cosγz − vt) in cui compaiono gli angoli tra la direzione di propagazione dell’onda e gli assi cartesiani. Funzioni di questo tipo sono soluzioni di equazioni differenziali di secondo ordine alle derivate parziali dette equazioni delle onde:

dove ∇² è l’operatore → laplaciano, che esprime le derivate seconde di ƒ rispetto alle variabili che definiscono la posizione.

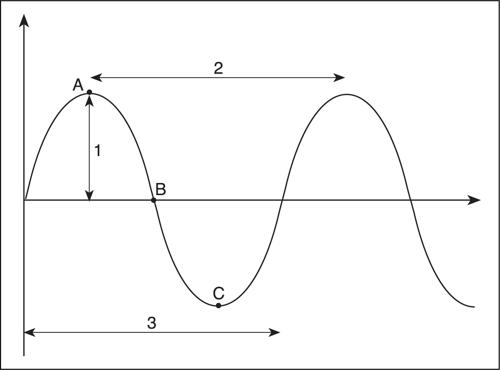
Si definisce fronte d’onda il luogo dei punti nei quali, a un dato istante, l’argomento della funzione è identico. Un’onda bidimensionale è detta rettilinea se i suoi fronti d’onda sono delle rette, mentre è circolare se i fronti sono delle circonferenze. Analogamente un’onda tridimensionale è detta piana o sferica se i suoi fronti sono rispettivamente dei piani o delle sfere. Di particolare interesse nelle applicazioni in fisica è lo studio delle onde periodiche, cioè di onde descritte da funzioni periodiche nell’argomento; tali funzioni devono necessariamente essere periodiche sia nella parte spaziale sia in quella temporale. Il periodo spaziale è detto lunghezza d’onda, mentre quello temporale è detto periodo dell’onda e il suo inverso, che rappresenta il numero di oscillazioni complete dell’onda nell’unità di tempo, è detto frequenza dell’onda. Il periodo T e la lunghezza d’onda λ sono legati alla velocità di propagazione dell’onda mediante la relazione ν = λ/T. Poiché una qualunque funzione periodica può essere scomposta nella somma di funzioni sinusoidali (→ Fourier, serie di), è particolarmente interessante lo studio delle onde sinusoidali che sono descritte da funzioni del tipo ƒ(x, t) = Asin(kx − ωt + φ), dove A è detta ampiezza dell’onda e rappresenta il valore massimo dell’oscillazione, k = 2π/λ è il numero d’onda, ω = 2π/T è la pulsazione e φ rappresenta una fase che dipende dalle condizioni iniziali.

In elettronica e nella teoria dei segnali è utile lo studio di due particolari onde periodiche: le onde quadre e quelle a dente di sega. Un’onda quadra è un’onda in cui si alternano regolarmente due valori costanti; matematicamente può essere rappresentata da una funzione del tempo del tipo:

Un’onda a dente di sega cresce linearmente fino a raggiungere un valore massimo, per poi azzerarsi e ricominciare a crescere; se, per esempio, la pendenza della crescita è pari alla metà del valore massimo dell’onda, essa assume una forma del tipo

La dipendenza dalla posizione in questi casi non compare poiché i segnali rappresentati da questo tipo di onde si propagano con velocità estremamente elevata e il valore dell’onda può essere considerato costante in tutti punti del circuito.

Il concetto di onda ha assunto un particolare significato nella fisica delle particelle: ogni particella si può presentare infatti sotto un duplice aspetto, ondulatorio e corpuscolare. Tale duplicità (nota come dualismo onda-particella) viene superata considerando che al movimento di una particella corrisponde la propagazione di un gruppo di onde e, viceversa, a una propagazione ondosa corrisponde uno sciame di particelle. Le equazioni (per esempio l’equazione di → Schrödinger) che regolano il moto di queste onde sono ricavate dall’equazione di d’→ Alembert, introducendo opportune correzioni derivate dalla teoria dei quanti, e costituiscono la base della meccanica ondulatoria e quantistica.