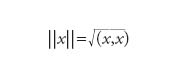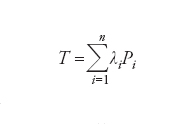operatore di proiezione
operatore di proiezione
Sia ℋ uno spazio vettoriale e P un’applicazione lineare (operatore) di ℋ in sé. Se P=P2 allora P è detto operatore di proiezione. Di particolare importanza è il caso in cui ℋ è dotato di un prodotto scalare (∙,∙) che induce una norma definita da
,
ossia è uno spazio di Hilbert ℋ. Un operatore di proiezione P hermitiano (autoaggiunto), ovvero tale che P*=P o equivalentemente (x,Py)=(Px,y) per ogni x,y∈ℋ, è detto proiettore ortogonale. Consideriamo ora il sottoinsieme di ℋ definito da XP={x∈ℋ tali che Px=x} dove P è un proiettore ortogonale. Non è difficile verificare (P è lineare) che XP è un sottospazio lineare chiuso nella norma indotta dal prodotto scalare. Si ha inoltre (I−P)2=I−2P+P2=I−P, così che anche I−P è un proiettore (evidentemente ortogonale). Lo spazio lineare XI−P={x∈ℋ tali che (I−P)x=x} coincide con il complemento ortogonale di XP in ℋ: se x∈XI−P e y∈XP allora (x,y)=((I−P)x,Py)=(x,(I−P)Py)=(x,(P−P2)y)= =0 e tutti gli elementi di XI−P sono ortogonali a tutti gli elementi di XP. Viceversa, a ogni sottospazio chiuso X corrisponde un proiettore ortogonale PX (il proiettore su quello spazio). I proiettori (ortogonali) possono essere considerati i più elementari tra gli operatori su uno spazio di Hilbert e corrispondono alle funzioni caratteristiche nella teoria delle funzioni di una variabile reale. La funzione caratteristica χX di un sottoinsieme X della retta reale ℝ è definita da χX(x)=1 se x∈X e χX(x)=0 altrimenti. Notiamo che χX(x)2=χX(x). Siano ora Pi(i=1,...,n) dei proiettori ortogonali tali che PiPj=0 per ifij e λi (i=1,...,n) dei numeri complessi: si può allora considerare l’operatore
Più in generale un operatore T è detto diagonalizzabile se ammette una decomposizione in termini di proiettori ortogonali analoga alla precedente. Se λi∈ℝ per tutti gli i, l’operatore T è hermitiano. Il teorema spettrale è una generalizzazione della decomposizione precedente per operatori hermitiani continui (limitati) qualunque e può essere interpretato come l’analogo per operatori della rappresentazione di una funzione (boreliana) di una variabile reale in termini di (limiti di) somme di funzioni caratteristiche di insiemi misurabili (boreliani). Viceversa, l’insieme delle funzioni caratteristiche di insiemi misurabili (boreliani) su uno spazio topologico X genera in un senso opportuno l’insieme (l’algebra commutativa) delle funzioni misurabili su X. Tale proposizione ha un analogo non commutativo: ogni algebra di von Neumann su uno spazio di Hilbert ℋ è generata dai proiettori ortogonali appartenenti a essa.