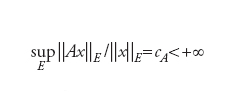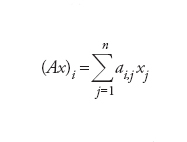operatori lineari
operatori lineari
Un’applicazione A:E→F di uno spazio lineare E in uno spazio lineare F (anche coincidente con E) su un campo K (che qui identificheremo con i numeri complessi ℂ) tale che A(αx1+βx1)1= αAx1+βAx2 (x1,x2∈E). L’insieme D(A) di tutti gli x∈E per i quali l’applicazione è definita si dice dominio di definizione dell’operatore A. Non sempre D(A)=E, ma faremo questa assunzione nel seguito. Con questa semplificazione, le nozioni di somma e prodotto di operatori lineari sono definite in modo ovvio. L’insieme degli x∈E tali che Ax=0 è detto nucleo di A e si indica KerA, l’insieme degli y∈F tali che y=Ax si chiama immagine di A e si denota ImA. Entrambi sono sottospazi lineari di E e F rispettivamente. Se gli spazi E e F sono dotati di una topologia, l’operatore A si dirà continuo in un punto x0∈E se per ogni intorno V del punto y0=Ax0 esiste un intorno U di x0 tale che Ax∈ V per x∈ U. L’operatore è detto continuo se è continuo in ogni x∈E. In questo caso KerA è un sottospazio chiuso di E. Dalla proprietà di linearità segue che A è continuo se e solo se è continuo in un singolo punto x0. Se E e F sono spazi normati questa definizione è equivalente alla seguente: l’operatore A è detto continuo se per ogni ε>0 esiste δ>0 tale che ∣∣x1−x2∣∣〈δ implica ∣∣Ax1−Ax2∣∣〈ε. In questo caso la continuità è equivalente alla limitatezza: un operatore lineare tra spazi di Banach E e F è continuo se e solo se
Il numero reale cA definisce una norma dell’operatore A; dotato di questa norma, l’insieme degli operatori lineari continui tra due spazi di Banach costituisce un esempio di algebra di Banach (non commutativa). Se A manda lo spazio vettoriale n-dimensionale complesso ℂn con base (e1,...,en) nello spazio m-dimensionale ℂm con base (f1,...,fm) esistono numeri complessi ai,j (i=1,...,m e j=1,...,n) tali che
dove xi indica l’i-esima coordinata di x∈ℂn. A può dunque essere rappresentato come una matrice di n colonne e m righe. L’operatore di derivazione d/dx può essere considerato come operatore sullo spazio C([a,b]) delle funzioni continue su un intervallo [a,b]: in questo caso D(d/dx)fiC([a,b]) poiché una funzione continua non è sempre derivabile. Di fondamentale importanza è poi la nozione di operatore inverso A−1 di un operatore dato A. In particolare A:E→F è detto invertibile se per ogni y∈F l’equazione Ax=y ha soluzione unica. La soluzione si indica con il simbolo x=A−1y e definisce appunto un operatore. Ricordiamo infine è il seguente teorema: se A è lineare e limitato e trasforma biunivocamente uno spazio di Banach E in uno spazio di Banach F l’operatore A−1 è a sua volta limitato.