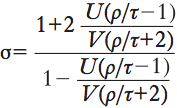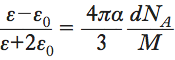Mossotti, Ottaviano Fabrizio
Ottaviano Fabrizio Mossotti
Mossotti fu una figura scientifica di rilievo nell’ambito della fisica matematica di metà Ottocento. Oggi è noto soprattutto per la relazione di Clausius-Mossotti, che serve a calcolare la costante dielettrica media di un sistema di sfere immerse in un medium omogeneo. I suoi risultati scientifici ebbero profonda influenza sullo studio delle interazioni molecolari. A più riprese, durante la sua vita, si venne anche a trovare coinvolto in moti indipendentistici: nel 1823 fu costretto dalla polizia austriaca a fuggire da Milano, nel 1848 comandò il Battaglione universitario toscano nella battaglia di Curtatone, e nel 1861, appena prima dell’Unità d’Italia, fu nominato senatore del Regno di Sardegna.
La vita
Ottaviano Fabrizio Mossotti, figlio dell’ingegnere Giovanni e di Rosa Gola, nacque a Carpignano Sesia il 18 aprile 1791. Conseguì la laurea (con lode) in fisica-matematica all’Università di Pavia nel 1811. Nella stessa città seguì i corsi di specializzazione di Alessandro Volta, Luigi Valentino Brugnatelli e Vincenzo Brunacci. Nel 1813, venne assunto all’Osservatorio astronomico di Brera a Milano dove partecipava alla redazione delle effemeridi annuali. A quei tempi ambiva a diventare professore presso l’Università di Pavia; tuttavia, nonostante il parere favorevole della facoltà, la Commissione reale negò il nulla osta per il fatto che Mossotti era straniero, cittadino cioè del Regno di Sardegna, mentre Pavia faceva parte del Regno Lombardo-Veneto. Restò dunque a Brera, dove progredì da terzo a primo allievo (1819). Le sue pubblicazioni astronomiche gli valsero una fama scientifica notevole. Venne quindi eletto membro della Società italiana delle scienze residente in Modena (detta anche Società dei XL) nel 1822.
Durante la sua permanenza a Milano, venne a contatto con un gruppo massonico-politico (Società dei Filadelfi, poi divenuta Società segreta dei Sublimi maestri, o dei Massoni perfetti) i cui scopi si allineavano con la maggior parte dei gruppi resistenti dell’epoca: rovesciamento del regime locale e introduzione di un governo popolare. Tali gruppi erano fortemente osteggiati dalla legge, che prevedeva pene severissime per gli affiliati. Il 18 gennaio 1823 l’affiliato Alexandre-Philippe Andryane (1797-1863), a Milano con il grado di diacono territoriale, che gli permetteva di creare nuovi membri, e con la missione di ricostituire la società, venne arrestato e interrogato. Trovarono tra le sue carte un biglietto recante il nome di alcune persone, tra cui Mossotti. Il 24 marzo 1823 Mossotti fu convocato dalla polizia per essere a sua volta interrogato; fortunatamente si trovava allora a Carpignano Sesia in villeggiatura. Di ritorno, trovata la convocazione, chiese consiglio a Barnaba Oriani (suo superiore all’Osservatorio), che gli consigliò la fuga. Oriani e Angelo De Cesaris, direttore dell’Osservatorio, omisero di avvisare le autorità, cui al contrario comunicarono che Mossotti non era mai tornato da Carpignano. Egli ne approfittò per fuggire rocambolescamente in Piemonte, da lì in Svizzera, quindi a Parigi e infine a Londra.
A Londra diede lezioni private e lavorò per l’Ammiragliato e per l’Ufficio della longitudine. Fu apprezzato e stimato dai colleghi, tra cui John Herschel e Thomas Young, e fu associato alla Royal astronomical society. Conoscendone il valore di scienziato e la situazione precaria, il barone Franz von Zach (figura di spicco nell’ambiente scientifico europeo del 19° sec.) lo raccomandò al console argentino. Mossotti giunse a Buenos Aires nel 1827 e vi restò sette anni: prima come ingegnere astronomo, e poi, dal 1834, come professore di fisica sperimentale. Nello stesso anno, lo Stato pontificio gli offrì la cattedra di astronomia dell’Università di Bologna.
Mossotti tornò in Italia, ma al suo arrivo scoprì che il posto non era più disponibile: il cardinale Carlo Opizzoni, responsabile dell’Università, era stato informato dal governo lombardo-veneto della sua fuga nel 1823 per motivi politici, fatto che lo rendeva inadatto all’impiego. Mossotti ottenne così un indennizzo di 2500 scudi romani (Vannucci 1878, 2° vol., p. 93), che corrispondevano a quattro anni di stipendio. Gli fu quindi offerto un incarico come professore all’Università Ionia di Corfù, dove arrivò nel 1836; là incontrò e si sposò con Ann Sutter, che morì di parto poco dopo. A Corfù si dedicò all’insegnamento e pubblicò un manuale di fisica (Lezioni elementari di fisica matematica, 2 voll., 1843-1845) che soddisfaceva un bisogno sentito sia in Italia sia all’estero. Nel 1840 fu nominato socio dell’Accademia delle scienze di Torino e nel 1841 fu chiamato alla cattedra di fisica matematica e meccanica celeste dell’Università di Pisa, dove restò fino alla morte. Cofondò nel 1844 il giornale «Il Cimento», che però ebbe vita breve; un secondo e più fortunato tentativo fu chiamato «Il Nuovo Cimento», fondato nel 1855. Durante la Prima guerra di indipendenza, nel 1848, al comando del Battaglione universitario toscano, combatté a Curtatone. Venne nominato senatore del Regno di Sardegna nel 1861 e morì il 20 marzo 1863, ricevendo tutti gli onori della città di Pisa.
L’attività politica
Il primo episodio significativo dell’esperienza politica di Mossotti fu la fuga da Milano del 1823, che avvenne in circostanze poco chiare. Convocato dalla polizia milanese per essere interrogato in seguito al ritrovamento di un biglietto recante il suo nome in possesso di Andryane, affiliato alla Società dei Filadelfi, Mossotti non si presentò, e anzi fuggì da Milano. La Società dei Filadelfi, poi divenuta dei Sublimi maestri, di ispirazione massonica e con scopi rivoluzionari, era nata come molte altre dopo la delusione napoleonica. Prima della caduta di Napoleone esse erano utili al governo austriaco, che perciò le sovvenzionava; durante la restaurazione l’atteggiamento austriaco verso tali società, che proponevano sistemi di governo democratici, cambiò radicalmente. Il Gran maestro della società era Filippo Buonarroti (che soleva farsi chiamare Michelangelo) il quale, nel 1814, era fuggito a Ginevra dove si manteneva insegnando canto; di là cercava di coordinare tutte le società segrete democratiche in Italia e in Francia.
Mandò così a Milano il giovane emissario Andryane, suo allievo di canto, con lo scopo di riannodare le fila della società a Milano. Secondo i rapporti di polizia (Liberti 1995) e secondo Andryane (Mémoires d’un prisonnier d’État, 1° vol., 18402), Buonarroti fornì ad Andryane i codici segreti della società, che si trovano ora all’Archivio di Stato di Milano, e un biglietto recante alcuni nomi di possibili simpatizzanti da affiliare, tra cui Mossotti. Come Buonarroti potesse conoscere Mossotti non è noto. È possibile che Giuseppe Pecchio, affiliato alla società, lo avesse incontrato in uno dei salotti liberali e ne avesse sondato le idee politiche. Andryane nelle sue memorie afferma che, sebbene si fosse incontrato con Mossotti, non avevano mai parlato di politica; e inoltre che non era stato lui a scrivere il suo nome sul biglietto, ipotizzando che fosse stato Buonarroti o qualcuno dei rifugiati italiani prima della sua partenza. Non è completamente chiaro nemmeno il modo in cui Mossotti era entrato negli ambienti liberali: da alcune lettere trovate all’Osservatorio di Brera sembra che gli astronomi non fossero ignoti a Didina Calderara, che teneva un salotto letterario-liberale e che fuggì dall’Italia dopo il 1821.
Non è facile stabilire se Mossotti fosse stato affiliato alla società massonica o meno (Liberti 1995). Vi sono ragioni per affermarlo, quali la sua fuga precipitosa, interpretata dal magistrato imperiale Antonio Salvotti von Einchenkraft und Bindenburg come un’ammissione di colpevolezza; la sua documentata simpatia per gli ambienti liberali (pubblicò diversi articoli sul giornale liberale «Il Conciliatore», sovvenzionato dal conte Luigi Porro Lambertenghi, di cui Mossotti era grande amico); alcune illazioni presenti in un rapporto di polizia del 1832 (Liberti 1995) sulla sua presunta iniziazione alla società officiata da Pecchio; la sua partecipazione attiva ai moti del 1848. Ma vi sono anche buone ragioni per dubitarne: Andryane negò sempre, sia sotto interrogatorio sia nelle sue memorie, di aver mai affiliato Mossotti; a differenza di altri nomi trovati sul biglietto in mano ad Andryane, Mossotti era l’unico incensurato al momento della convocazione di polizia; non vi è alcun riferimento a una sua partecipazione attiva ai moti del 1821, di cui testimonia anche il rapporto di polizia (Liberti 1995). D’altro canto, quando Salvotti chiamava a deporre, data la facilità con cui spediva i sospetti al carcere dello Spielberg, era saggio scappare.
Si potrebbe ipotizzare che Mossotti non fosse mai stato affiliato alla società ma che, date le sue frequentazioni, avesse deciso di fuggire per evitare l’interrogatorio, la probabile tortura e la possibilità della condanna al carcere duro (Liberti 1995).
La sua partecipazione alla battaglia di Curtatone nel 1848 è ben documentata. In ragione della sua autorevolezza (era senatore nel Parlamento di Toscana) a Mossotti venne affidato il comando, con il grado di maggiore, del Battaglione universitario toscano, che schierò elementi di Pisa e di Siena. Il suo allievo Enrico Betti, che divenne in seguito un famoso matematico, partecipò alla battaglia con il grado di caporale.
Nonostante la superiorità numerica degli Austriaci, l’esercito piemontese-toscano oppose un’eroica resistenza. A colleghi e studenti che per via dell’età (aveva poco meno di sessant’anni) gli volevano risparmiare il fuoco nemico, rispose: «se state nel pericolo voi, figli miei, perché vi abbandonerò io che son vostro padre?». Secondo una testimonianza (Vannucci 1878, 2° vol., p. 95), mentre infuriava la battaglia Mossotti disegnava figure geometriche per terra con la punta della spada. Alcuni sostengono che Mossotti fu ferito ma solo di striscio, altri che rimase incolume. Il suo battaglione subì delle perdite e ricevette l’ordine di ripiegare su Goito.
L’attività scientifica
Secondo la testimonianza dei colleghi (il suo maestro Brunacci a Pavia, alcuni astronomi dell’Osservatorio di Brera, Gabrio Piola e Betti) Mossotti fu un matematico di eccezionale levatura. A livello internazionale ottenne riconoscimenti simili da parte di Karl Friedrich Gauss, Franz Xaver von Zach, Michael Faraday, Giovanni Antonio Amedeo Plana, Dominique-François Arago, James Clerk Maxwell e molti altri. Betti, per es., nel suo elogio funebre, lascia capire che, se Mossotti si fosse dedicato maggiormente all’analisi, avrebbe fatto scoperte importanti: «Prima di Abel e Jacobi, egli aveva avuto l’idea di considerare la funzione inversa degli integrali ellittici di prima specie». Jules-Henri Poincaré scrisse: «È probabile che Maxwell sia stato condotto alla sua teoria [del campo elettromagnetico] grazie alla concezione di Poisson e Mossotti sulla natura dei mezzi dielettrici» (Cours de physique mathématique, 1901, p. 36), precisando anche che, matematicamente, la teoria di Maxwell è identica a quella di Poisson e Mossotti.
Come anticipato, il nome di Mossotti è tuttora noto per la formula di Clausius-Mossotti. Essa si applica in maniera analoga alla costante dielettrica e alla permittività media di un sistema composto da un insieme di sfere immerse in un medium omogeneo. La relazione tra costante dielettrica media del sistema e costante dielettrica delle sfere e del medium è descritta in Discussione analitica sull’influenza che l’azione di un mezzo dielettrico ha sulla distribuzione dell’elettricità alla superficie di più corpi elettrici disseminati in esso («Memorie della Società italiana delle scienze», 1850, 2, pp. 49-74) e Rudolf Clausius ne dà per la prima volta la formulazione esplicita (Die mechanische Wärmetheorie, 2° vol., 1879). Nell’interpretazione di Clausius, la relazione lega la permittività del sistema con la permittività delle sfere e del medium.
Non meno importanti furono gli studi d’idraulica: ancora uditore a Pavia, seguendo gli insegnamenti del suo maestro Brunacci (che partecipò alla commissione incaricata del progetto del Naviglio Pavese a Milano), pubblicò una nota sull’ariete idraulico (Nota sopra un problema nella teorica dell’ariete idraulico, in V. Brunacci, Trattato dell’ariete idraulico, 1810, pp. 70-73), una pompa idraulica in grado di sfruttare la forza cinetica del flusso del liquido entrante. Inventata nel 1772 e brevettata nel 1797, aveva suscitato a quei tempi un grande interesse, dato che non aveva bisogno di alcun intervento di forze esterne.
Mossotti dedicò rilevanti studi anche a problemi di astronomia. Nel 1816, all’Osservatorio di Brera, pubblicò un metodo innovativo per determinare le orbite dei corpi celesti (Nuova analisi del problema di determinare le orbite dei corpi celesti, in F. Carlini, E. Brambilla, Effemeridi, 1817): l’articolo fu oggetto di una diffusione internazionale, tanto che anche Gauss ne diede un riassunto esteso (Effemeridi astronomiche di Milano per l’anno 1817 calcolate da Francesco Carlini ed Enrico Brambilla, «Göttingische gelehrte Anzeigen», 1817, 144, pp. 1433-38). I metodi precedenti si basavano su tre osservazioni sufficientemente vicine (affinché l’approssimazione di un angolo al suo seno fosse valida), ma si ottenevano comunque equazioni di grado elevato, non risolubili analiticamente. Il metodo di Mossotti, utilizzando quattro osservazioni, permette di ottenere equazioni di primo grado.
A Londra, le causali dei pagamenti a Mossotti dal conto bancario dell’Ammiragliato presso Coutts menzionano un «lavoro editoriale nelle osservazioni del Prof. Mayer», che si presume essere riferito a Tobias Mayer, astronomo tedesco del Settecento. A Buenos Aires pubblicò diverse osservazioni astronomiche, prevalentemente nei Memoirs of the Royal astronomical society, ma anche nei Comptes-rendus de l’Académie des sciences. In particolare, in questi ultimi, pubblicò una memoria sul clima di Buenos Aires, comunicata da Arago in persona (il segretario dell’Accademia), con cui Mossotti era in contatto fin dai tempi di Londra.
Le ricerche sulla coesione molecolare contenute nel saggio Sur les forces qui régissent la constitution intérieure des corps (1836), pubblicato mentre Mossotti lavorava a Corfù, ebbero risonanza internazionale. Faraday ne era entusiasta e il 13 dicembre 1836 scrisse a William Whewell:
Non posso esimermi dallo scriverle. Ho appena ricevuto un breve articolo dal Sig. Mossotti di Torino sulle forze che governano la materia. Lo ha visto? Ne sono rimasto molto colpito […] Parla dell’elettricità, e deduce da essa tutti i fenomeni di gravitazione (L.P. Williams, The selected correspondence of Michael Faraday, 1° vol., 1971).
Faraday fece tradurre l’opera e la trasmise alla Royal institution di Londra nel 1837. Vista la direzione attuale della fisica riguardo alle GUT (Grand Unification Theories), l’articolo di Mossotti del 1836, che proponeva un’unificazione delle forze elettrica e gravitazionale, era notevolmente in anticipo rispetto al suo tempo. Partendo dal principio che le molecole si attirano quando sono distanti e si repellono quando sono vicine, Mossotti conclude che deve esistere un punto intermedio in cui le molecole restano a un equilibrio stabile. Più precisamente, sempre nel saggio del 1836 (sezione 3), egli afferma:
Consideriamo molte molecole materiali, che si repellono a vicenda, immerse in un fluido elastico i cui atomi si repellono a vicenda, ma che sono attirati dalle molecole materiali. Tutte queste forze d’attrazione e di repulsione sono proporzionali alle masse in ragione del reciproco del quadrato della distanza; e vediamo se le azioni che hanno luogo tra molecole materiali possono portarle in uno stato di equilibrio stabile (p. 164).
Mossotti scrive un sistema di equazioni differenziali, che non possono essere risolte in generale per via analitica. Per delle molecole di forma sferica, nel punto di equilibrio «ogni molecola condensa intorno a sé un’atmosfera di etere la cui densità, assai notevole presso la superficie, decresce rapidamente con la distanza» (Derenzini 1964, p. 233). La decrescita rapida di questa soluzione approssimata si deve ad alcuni esponenziali negativi in funzione della distanza, che moltiplicano i termini della funzione.
Formula di Clausius-Mossotti
Il lavoro per cui Mossotti gode ancora oggi di notorietà (Discussione analitica sull’influenza che l’azione di un mezzo dielettrico ha sulla distribuzione dell’elettricità alla superficie di più corpi elettrici disseminati in esso, cit.), è quello in cui viene descritta per la prima volta la relazione che poi Clausius scriverà in modo compatto (Die mechanische Wärmetheorie, cit.), dando luogo alla formula di Clausius-Mossotti (CM). Uno degli aspetti più interessanti di quest’opera è che Mossotti partì da ipotesi ormai ampiamente falsificate (esistenza dell’etere), o comunque prive di prove sperimentali (decomposizione del fluido elettrico e magnetico «in due fluidi vitreo o resinoso, boreale o australe»), per arrivare, grazie al suo intuito fisico-matematico fuori dal comune, a importanti risultati che descrivono correttamente una relazione tra quantità medie in una situazione ideale.
Nella letteratura scientifica odierna, si trovano tante versioni della formula di CM quanti sono gli autori che ne scrivono. Nell’articolo A numerical verification of the Clausius-Mossotti relation (Steffan, Richter 1990) la formula di CM per calcolare la conduttività media σ di un sistema di sfere di conduttività ρ e volume U immerse in un medium di conduttività τ e volume V−U è come segue:
La formulazione più comune della formula di CM si riferisce a una massa molare M di una sostanza di densità d, costante dielettrica ε e polarizzabilità molecolare α nel vuoto (la cui permittività è ε0):
dove NA è il numero di Avogadro.
Anche di recente sono stati pubblicati articoli scientifici sulla formula di CM sia in fisica (Steffan, Richter 1990; Reddy et al. 2003), sia in matematica (Felderhof, Ford, Cohen 1983). Quest’ultimo articolo, in maniera particolare, estende alcune parti del risultato di Mossotti a un campo elettrico dinamico (anziché statico), attraverso considerazioni di ordine combinatorio sulle maniere di raggruppare n sfere. Richard Feynman dà una derivazione della formula di CM nel secondo volume delle sue famose Lectures on physics (1964).
Ottica
La monografia di Mossotti sull’ottica (Nuova teoria degli strumenti ottici, 1857) è strutturata in quattro parti: ‘Analisi del corso di un raggio di luce che attraversa uno stromento [sic] ottico’, ‘Prima approssimazione’, ‘Seconda approssimazione’, ‘Esempi di calcolo di lenti aplanatiche’. Di questo lavoro Giovanni Codazza, nella Commemorazione di Ottaviano Fabrizio Mossotti, dice:
Tutti i lavori sulla teoria degli strumenti ottici prima di Biot e Gauss contenevano restrizioni che ne rendevano meno esatte le deduzioni per le applicazioni pratiche. […] Mossotti determina quattro coppie di equazioni […] le quali assegnano le condizioni perché l’immagine prodotta da un sistema di lenti costituisca una rappresentazione simile all’oggetto (1863, p. 18).
Seguendo la teoria ottica di Mossotti venne costruito un obiettivo da sei pollici di apertura e un oculare accoppiato che producevano, verso la fine dell’Ottocento, effetti molto soddisfacenti.
Opere
Nota sopra un problema nella teorica dell’ariete idraulico, in V. Brunacci, Trattato dell’ariete idraulico, Milano 1810, pp. 70-73.
Nuova analisi del problema di determinare le orbite dei corpi celesti, in F. Carlini, E. Brambilla, Effemeridi, Milano 1817.
Sur les forces qui régissent la constitution intérieur des corps; aperçu pour servir à la détermination de la cause et des lois de l’action moléculaire, Turin 1836.
Lezioni elementari di fisica matematica, 2 voll., Firenze 1843-1845.
Discussione analitica sull’influenza che l’azione di un mezzo dielettrico ha sulla distribuzione dell’elettricità alla superficie di più corpi elettrici disseminati in esso, «Memorie della Società italiana delle scienze», 1850, 2, pp. 49-74.
Nuova teoria degli strumenti ottici, Pisa 1857.
Scritti, a cura di L. Gabba, G. Polvani, 2 voll., Pisa 1942-1955.
Bibliografia
G. Codazza, Commemorazione di Ottaviano Fabrizio Mossotti letta nella seduta del 23 aprile 1863 al Reale Istituto lombardo di scienze e lettere, «Il Politecnico», 1863, pp. 245-66.
A. Vannucci, I martiri della libertà Italiana dal 1794 al 1848, 2° vol., Milano 1878.
T. Derenzini, Le forze molecolari secondo Ottaviano Fabrizio Mossotti: a proposito di una lettera di Amedeo Avogadro, «Physis», 1964, 2, pp. 229-36.
B. Felderhof, G. Ford, E. Cohen, The Clausius-Mossotti formula and its nonlocal generalization for a dielectric suspension of spherical inclusions, «Journal of statistical physics», 1983, 33, pp. 241-60.
J. Steffan, K. Richter, A numerical verification of the Clausius-Mossotti relation, «IEEE Transactions on magnetics», 1990, 2, pp. 528-31.
L. Liberti, Ottaviano Fabrizio Mossotti: the youth years (1791-1823), Bachelor of science thesis, Imperial college, London 1995, http://www.lix.polytechnique.fr/ ~liberti/maths-history/mossotti/mossotti.html (19 marzo 2013).
R. Reddy, Y. Nazeer Ahammed, K. Rama Gopal, P. Abdul Azeem, B. Sasikala Devi, T. Rao, S. Behere, On the equivalence between Clausius-Mossotti and optical electronegativity relations, «Optical materials», 2003, 22, pp. 7-11.
L. Liberti, E.L. Ortiz, Mossotti Ottaviano Fabrizio, in Dizionario biografico degli Italiani, Istituto della Enciclopedia Italiana, 77° vol., Roma 2012, ad vocem.