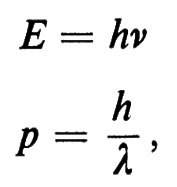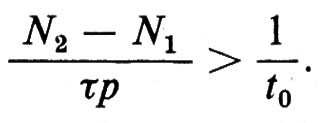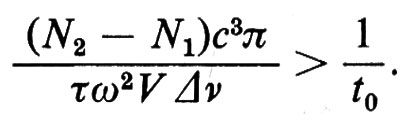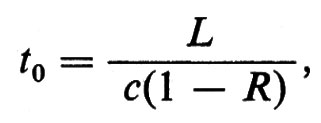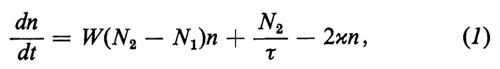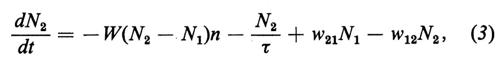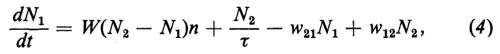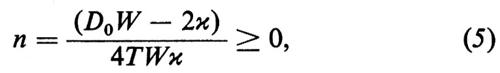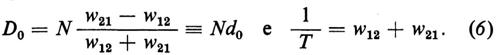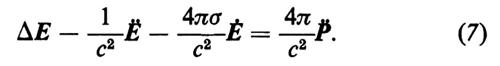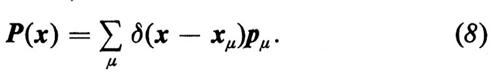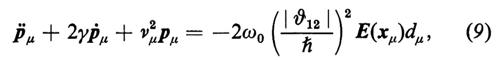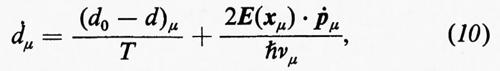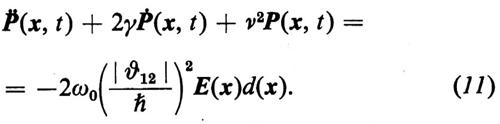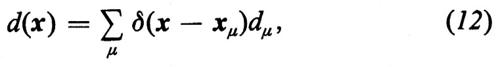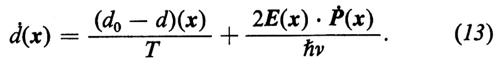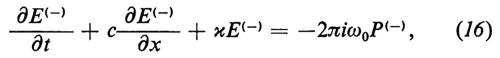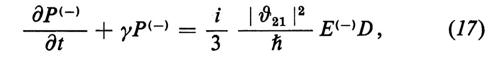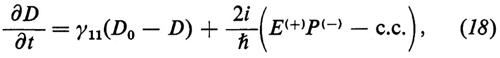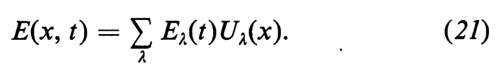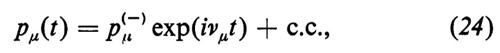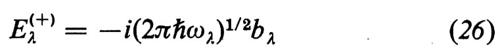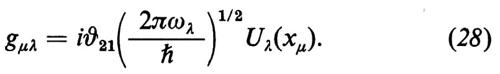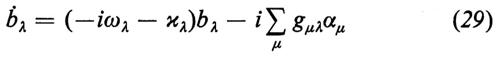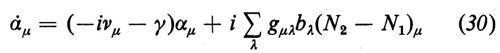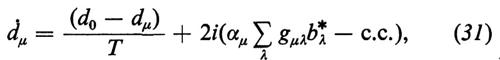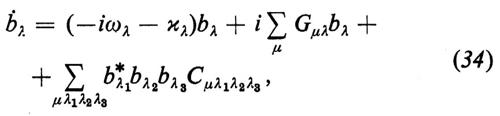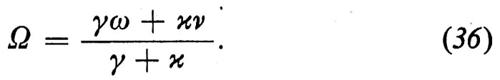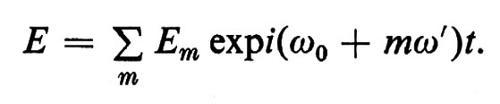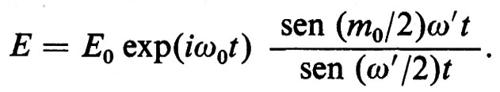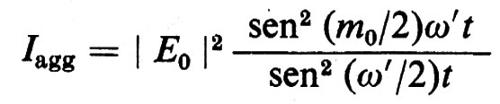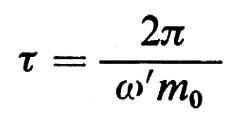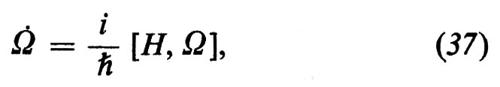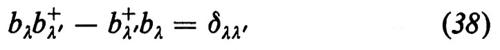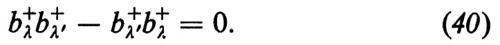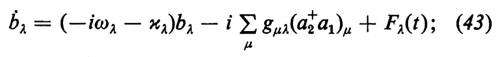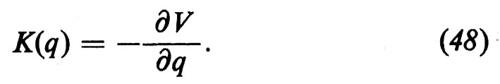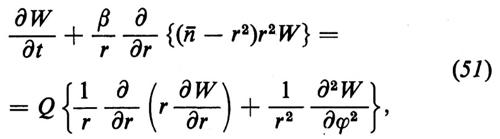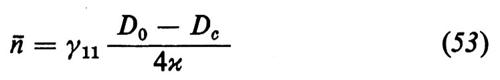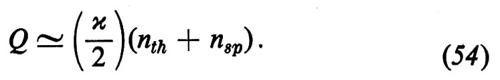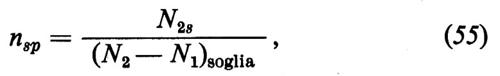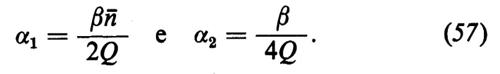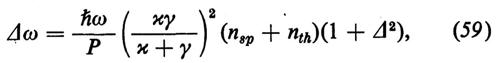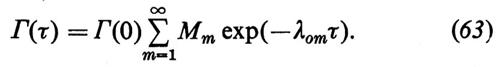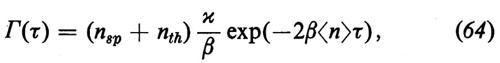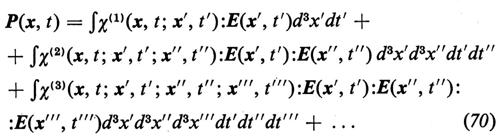Ottica quantistica
Ottica quantistica
di Hermann Haken
Ottica quantistica
sommario: 1. Ottica quantistica: la natura della luce. 2. Il laser. a) Il mezzo laser-attivo e i sistemi di pompaggio. b) II risonatore. c) Descrizione qualitativa del processo laser. Condizione laser. d) Caratteristiche principali della luce laser. e) La teoria del laser. 3. Ottica non lineare. a) Analogia tra atomi a due livelli e particelle a spin 1/2. b) Effetto Stark dinamico. c) Bistabilità ottica. d) Interazioni non lineari delle onde. e) Assorbimento di due o più fotoni. f) Spettroscopia laser. g) Ulteriori applicazioni fisiche della luce laser. 4. Applicazioni della luce laser in altre discipline. □ Bibliografia.
1. Ottica quantistica: la natura della luce
L'ottica quantistica, nel suo significato più generale, studia quei fenomeni in cui entrano in gioco la natura quantistica della luce e la sua interazione con la materia. (Per quel che riguarda la natura quantistica della luce, v. quanti, teoria dei: Elettrodinamica quantistica).
Oggetti come atomi, molecole o solidi devono essere trattati mediante la meccanica quantistica per poterne descrivere in maniera adeguata l'interazione con la luce. Le idee sviluppate nei primi studi dell'ottica quantistica hanno portato all'invenzione di sorgenti elettromagnetiche di tipo interamente nuovo nella regione delle microonde (maser) e del visibile (laser). Le proprietà fisiche della luce laser differiscono in maniera fondamentale da quelle della luce prodotta da sorgenti convenzionali, come le normali lampade o il Sole, e sono all'origine di effetti del tutto nuovi che formano l'oggetto dell'‛ottica non lineare'.
In questo articolo tratteremo dell'ottica quantistica in senso stretto; del laser, incluse le proprietà fisiche della luce laser; dei più importanti aspetti dell'ottica non lineare e di alcune importanti applicazioni del laser nella tecnologia, nella medicina, ecc.
La luce visibile occupa quella parte dello spettro totale delle onde elettromagnetiche compresa nell'intervallo di frequenze tra ν=3,75×1014 s-1 e ν=7,5×1014 s-1. Secondo l'elettrodinamica quantistica, i campi elettromagnetici possono avere sia le proprietà delle onde, sia quelle delle particelle (fotoni). La teoria ondulatoria della luce si basa sulle equazioni di Maxwell dell'elettromagnetismo; il carattere ondulatorio della luce e sperimentalmente dimostrato dai fenomeni di interferenza e di diffrazione, mentre quello corpuscolare viene messo in evidenza, per esempio, nei processi di urto tra la luce e gli elettroni (o altre particelle elementari), come nell'effetto Compton. Questi due aspetti della luce costituiscono quello che si chiama dualismo onda-particella. Quale di questi due aspetti si incontri dipende dal tipo di esperimento che si esegue. Le ‛regole di trascrizione' dagli aspetti ondulatori (frequenza ν, lunghezza d'onda λ) a quelli corpuscolari (energia E, quantità di moto p), e viceversa, sono:
dove h è la costante di Planck.
La descrizione dell'interazione tra la luce e gli atomi (e più in generale la materia) richiede una trattazione quantomeccanica. Un singolo atomo è costituito da un nucleo carico positivamente e da vari elettroni che gli orbitano intorno. Nel seguito considereremo, per semplicità, un unico elettrone. A differenza di quanto accade nella meccanica classica, nella teoria quantistica un elettrone legato può occupare solo degli stati stazionari con energie di legame ‛discrete'. Quando un elettrone salta da uno stato stazionario a a un altro b viene emessa luce; secondo Bohr, la frequenza ν della luce emessa in questo processo è data dalla relazione hν=Ea−Eb, dove Ea ed Eb sono le energie degli stati iniziale e finale dell'elettrone e h è la costante di Planck introdotta sopra. La luce può essere assorbita da un elettrone che compia una transizione da uno stato di energia minore a uno di energia maggiore. Un fotone che colpisca un atomo può provocare la cosiddetta ‛emissione stimolata', processo in cui viene creato un nuovo fotone; anche in questo caso la relazione hν=Ea−Eb deve essere soddisfatta. Dobbiamo quindi distinguere tre processi elementari: 1 emissione spontanea di luce (in cui viene emesso un fotone), l'emissione stimolata (in cui sono presenti uno o più fotoni e viene creato un nuovo fotone) e l'assorbimento (in cui sono presenti uno o più fotoni e un fotone viene assorbito). Secondo il dualismo onda-particella, questi processi possono essere trattati teoricamente mediante una descrizione in termini di onde o di fotoni. Nella descrizione ondulatoria, la luce emessa spontaneamente da un atomo consiste di un pacchetto di onde di lunghezza finita. Analizzando un pacchetto di lunghezza finita nelle sue componenti di diversa frequenza (analisi di Fourier), si trova in genere un ampio intervallo di frequenze di larghezza Δw. Il quadrato del modulo dei coefficienti di Fourier è proporzionale alla probabilità di trovare un fotone della frequenza corrispondente.
Quando più atomi formano una molecola o un solido, in particolare un cristallo, il moto degli elettroni di ciascun atomo viene mutato e, similmente, i livelli energetici atomici originali sono sostituiti da nuovi schemi di livelli energetici. Nei cristalli si formano delle bande continue di livelli energetici, separate le une dalle altre da ‛zone proibite'. Le transizioni di elettroni tra questi livelli possono essere anch'esse accompagnate dall'emissione o dall'assorbimento di un fotone, purché siano rispettate certe ‛regole di selezione'.
La teoria quantistica si applica anche a particelle diverse dagli elettroni, come protoni, neutroni o interi atomi. Quando più atomi formano una molecola, si possono verificare delle oscillazioni atomiche interne (vibrazioni), oppure delle rotazioni dell'intera molecola. Le energie corrispondenti sono quantizzate e anche in questo caso si possono verificare delle transizioni ottiche (cioè transizioni collegate con l'emissione o l'assorbimento di luce), la cui lunghezza d'onda si trova nella regione infrarossa.
Sono possibili anche transizioni ottiche che coinvolgano allo stesso tempo i moti dell'elettrone (o degli elettroni) e i moti vibrazionali (rotazionali).
I livelli energetici dei protoni e dei neutroni nei nuclei sono quantizzati e la separazione tra di essi è considerevolmente più grande di quella tra i livelli energetici elettronici in un atomo. Quindi l'energia dei fotoni emessi dai nuclei è molto più grande e la lunghezza d'onda della luce è molto più corta e cade nella banda dei raggi X e γ.
Da quanto detto sopra risulta chiaro che in natura esistono sistemi quantistici assai diversi le cui ‛transizioni ottiche' possono generare luce infrarossa, visibile, ultravioletta, raggi X e γ.
La luce può essere generata anche per Bremsstrahlung, o radiazione di frenamento, che si produce quando degli elettroni sono deviati per esempio dai campi elettrici di un nucleo, o per radiazione di sincrotrone, quando gli elettroni si muovono in campi magnetici.
2. Il laser
La parola ‛laser' è un'abbreviazione dell'espressione Light Amplification by Stimulated Emission of Radiation, che significa ‛amplificazione della luce per mezzo dell'emissione stimolata di radiazione'. Nei primi lavori venne usata l'espressione ‛maser ottico', dove ‛maser' sta per Microwave Amplification by Stimulated Emission of Radiation, che significa ‛amplificazione di microonde per mezzo di emissione stimolata di radiazione'. Nella letteratura sovietica viene usato anche il termine ‛generatore ottico'.
Il principio del maser si basa sul concetto di emissione stimolata, introdotto originariamente da Einstein (v., 1917).
In termini generali, sebbene un po' approssimativi, il principio in base al quale funziona un maser o un laser è il seguente: si considerino N sistemi quantici (atomi, molecole, ecc.) identici, o quasi identici, compresi in una regione dello spazio. Supponiamo che si possa verificare una transizione ottica tra due livelli di energia Ea ed Eb in ciascun sistema quantico e supponiamo inoltre che un'alta percentuale (più del 50%) dei sistemi quantici sia stata portata al livello di energia superiore. A questo punto i primi fotoni vengono emessi spontaneamente; essi colpiscono altri sistemi quantici eccitati provocando un'emissione stimolata di fotoni che a loro volta provocano un'ulteriore emissione stimolata e cosi via: si crea così una valanga di fotoni. Se dall'esterno si continua a fornire energia in quantità sufficiente, la produzione di fotoni continua per mezzo dell'emissione stimolata. Come vedremo più avanti, questo tipo di luce ha delle proprietà completamente nuove rispetto alla luce prodotta da sorgenti convenzionali, che emettono luce spontaneamente.
Il maser fu proposto da Basov e Prokhorov (v., 1954 e 1955), Townes (v. Gordon e altri, 1954), premi Nobel nel 1964, Weber (v., 1953) e Fabrikant (v., 1940). L'estensione del principio del maser alla regione ottica fu proposta da Schawlow e Townes (v., 1958).
Il laser è fondamentalmente costituito dalle seguenti parti: a) il mezzo laser-attivo; b) la sorgente pompante, o pompa; c) la cavità risonante.
Poiché variando il tipo di materiale laser-attivo cambia il sistema per pomparlo, discuteremo i punti a) e b) contemporaneamente.
a) Il mezzo laser-attivo e i sistemi di pompaggio
Il mezzo attivo consiste di certe sostanze capaci di emettere e di amplificare la luce in un dato intervallo di frequenze.
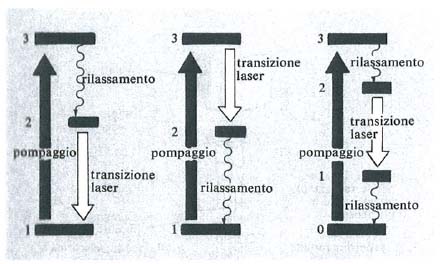
Transizioni elettroniche negli atomi. - In ciascun atomo almeno tre o quattro livelli elettronici intervengono nel processo totale. Come è indicato nella fig. 4, sono possibili diversi schemi di pompaggio, di decadimento ottico e di processi di rilassamento. Gli schemi di pompaggio mostrati nella fig. 4 sono detti ‛di pompaggio ottico' se una sorgente luminosa esterna svolge la funzione di pompa. Il pompaggio ottico fu introdotto per la prima volta da Kastler (v., 1950). Altri meccanismi di pompaggio saranno discussi più avanti in relazione ad esempi concreti.
Atomi laser-attivi possono trovarsi in un mezzo solido. Fra i laser a stato solido i più comuni sono i seguenti.
1. Laser a rubino. Il rubino fu il primo materiale nel quale sia stata dimostrata l'azione laser (v. Maiman, 1960). Il rubino è un cristallo formato da Al2O3 drogato con ioni Cr3+ in concentrazione tipica dello 0,05% in peso. Gli ioni di cromo danno al rubino il colore rosso. La luce emessa ha lunghezza d'onda λ=0,634 μm.
Generalmente il laser a rubino è pompato da intensi impulsi luminosi, che portano gli ioni di Cr3+ nel loro stato eccitato (che è in realtà sdoppiato). Gli ioni decadono poi al livello laser superiore, anch'esso suddiviso in due livelli, il più basso dei quali è il livello laser superiore indicato nel diagramma schematico. Lo stato fondamentale è il livello laser inferiore.
2. Laser a neodimio-vetro. Il vetro è drogato con ioni di neodimio che fungono da atomi laser-attivi. La luce emessa ha lunghezza d'onda λ=1,059 μm. Lo schema di pompaggio è quello mostrato nella fig. 4 a destra e generalmente si ottiene l'eccitazione per mezzo di sorgenti di luce incoerente che portano gli ioni dal loro livello di base al quarto livello (che è formato da diversi livelli).
3. Laser a neodimio-YAG. Ioni di neodimio immersi in granato di alluminio e ittrio (YAG) fungono da atomi laserattivi. La luce emessa ha lunghezza d'onda λ=1,0641 μm a temperatura ambiente. L'azione laser si può verificare quando il neodimio è disposto in maniera reticolare in cristalli di pentossido di neodimio.
4. Altri laser a stato solido. Altri esempi di questo gruppo sono dati da ioni di terre rare immersi in tungstenato di calcio e da ioni di U3+ in CaF2.
Gli atomi laser-attivi possono anche trovarsi in un mezzo allo stato gassoso. Il primo laser a gas era costituito da una miscela di gas elio e neon. Nel neon la transizione laser si verifica soprattutto per lunghezze d'onda λ=0,6328 μm, λ=1,15 μm e λ=3,39 μm. Il pompaggio degli atomi di neon avviene nel modo seguente: si stabilisce una scarica in continua o a radiofrequenza in una miscela di gas contenente, in genere, elio alla pressione di 1,0 mm di mercurio e neon a 0,1 mm. Gli elettroni della scarica eccitano gli atomi di elio in diversi stati eccitati. Molti si raccolgono nei livelli metastabili a vita lunga 23S, 2S e, poiché l'energia di questi stati metastabili coincide quasi con l'energia dei livelli 2S e 3S del neon, gli atomi di neon possono essere portati in questi due stati eccitati. L'eccitazione si verifica quando un atomo di elio eccitato urta contro un atomo di neon nello stato fondamentale e in questo processo trasferisce energia.
Transizioni elettroniche nelle molecole. - Gli eccimeri sono molecole biatomiche che possono esistere in stati eccitati, ma che hanno il livello fondamentale instabile. L'azione laser in sistemi a eccimeri fu dimostrata per la prima volta usando xeno liquido pompato da un fascio di elettroni. Da allora si è prodotta azione laser, per mezzo di fasci elettronici ad alta energia o di rapide scariche trasversali, in miscele gassose di Xe2, Kr2, Ar2 e in alogenuri di gas nobili, come XeBr, XeF, XeCl, KrF, KrCl, ArF. Questi laser possono operare nella regione dell'ultravioletto.
L'effetto laser è stato ottenuto anche utilizzando sostanze coloranti. In questo caso molecole di coloranti sono eccitate, in generale, da altri laser (per es. da laser ad argon) e possono emettere luce laser compresa in una banda abbastanza ampia di righe di emissione spontanea. Usando una combinazione di diversi tipi di coloranti si può coprire una regione di lunghezze d'onda compresa fra 4.300 Å e 8.000 Å. Esempi di questi coloranti sono diversi tipi di cumarina e rodamina, fluoresceina sodica, perclorato violetto e perclorato blu Nilo di Cresyl.
Azione laser basata su vibrazioni molecolari. - Il più importante fra i laser che esercitano un'azione basata su vibrazioni molecolari è il laser a CO2 gassosa. L'eccitazione avviene generalmente per mezzo di una scarica nel plasma, il quale, oltre a CO2, contiene normalmente N2 e He. La efficienza è eccezionalmente alta e si aggira attorno al 30%. Il laser a CO2 può anche essere fatto funzionare tenendo il gas sotto pressione; in questo caso l'allargamento della riga è molto più grande dell'allargamento Doppler. Si possono ottenere potenze di uscita particolarmente alte coi cosiddetti ‛laser a gas dinamico'. Una miscela ad alta temperatura e ad alta pressione di gas (in generale CO2, N2 e H2O oppure He) si espande molto rapidamente attraverso un ugello. Durante l'espansione si verifica un'inversione di popolazione nel gas, così che questo può essere utilizzato come mezzo laser-attivo. Il gas passa poi a velocità supersonica nella cavità laser (v. sotto) dove si crea un raggio di luce laser perpendicolare al flusso. Infine il gas entra in un diffusore dove viene rallentato.
Transizioni elettroniche in semiconduttori. - Nei semiconduttori i livelli energetici formano diverse bande; le più alte di tali bande si chiamano ‛banda di valenza' e ‛banda di conduzione'. Quando, per mezzo di un fascio di elettroni, gli elettroni semiconduttori sono portati da una banda di valenza a una banda di conduzione, si può verificare l'azione laser. In pratica l'inversione si ottiene generalmente nelle cosiddette giunzioni p-n, che si possono ottenere drogando dei semiconduttori (per es. GaAs) con atomi di impurità in concentrazioni e disposizioni spaziali ben definite in modo da deformare le bande energetiche. Quando si applica un campo elettrico esterno, gli elettroni possono saltare da una banda di conduzione a una banda di valenza, emettendo luce. In pratica, gli atomi di impurità sono coinvolti in queste transizioni. Se in una banda di valenza manca un solo elettrone, questa ‛lacuna' si comporta come una particella carica positivamente. La coppia legata elettrone-lacuna è nota col nome di ‛eccitone': gli eccitoni possono essere creati o annichilati nell'interazione con la luce. Quando il processo di decadimento si accoppia con altri processi di trasferimento di energia, per esempio con vibrazioni reticolari, diventa possibile l'azione laser degli eccitoni.
Laser a elettroni liberi. - L'ultimo esempio di laser che riportiamo è il cosiddetto laser a elettroni liberi, nel quale un fascio di elettroni viene fatto passare in un campo magnetico variabile nello spazio. Poiché cariche accelerate possono emettere radiazioni, si può avere in tal modo una sorgente di luce.
b) Il risonatore
In teoria la luce nella cavità risonante contiene tutte le lunghezze d'onda, tutte le direzioni di propagazione e tutte le direzioni di polarizzazione. Lo scopo principale del laser è di generare e di amplificare solamente luce con certe proprietà ben definite. Questa selezione, nella maggior parte dei casi, si ottiene o si facilita montando due specchi alle estremità del laser: nel caso più semplice si tratta di due specchi piani paralleli, che formano un ‛risonatore' aperto e che selezionano la luce in due modi. Secondo la teoria delle onde elettromagnetiche, nel cosiddetto interferometro di Fabry-Perot, consistente in due specchi piani paralleli, possono sostenersi solamente quelle radiazioni la cui lunghezza d'onda λ è tale che nλ/2=L, dove n è un numero intero ed L è la distanza fra i due specchi. Nel modello corpuscolare, i fotoni emessi secondo la direzione assiale sono costantemente riflessi tra i due specchi, mentre i fotoni che hanno altre direzioni si disperdono dopo breve tempo. Pertanto i fotoni che hanno direzione assiale hanno una probabilità molto maggiore di tutti gli altri di essere amplificati da un'emissione stimolata.
Per ottenere un alto coefficiente di riflessione (per luce polarizzata), si utilizza la riflessione all'angolo di Brewster, disponendo cioè gli specchi in modo che formino un particolare angolo con l'asse del laser.
Poiché inclinando gli specchi si può ridurre drasticamente la vita media dei fotoni nella cavità, si usano più spesso configurazioni più stabili degli specchi, quali il risonatore confocale o il laser ad anello.
I laser possono avere dimensioni diverse: i laser a semiconduttore hanno dimensioni di una frazione di millimetro, i laser a rubino hanno in generale una lunghezza di alcuni centimetri, mentre i laser a neodimio-vetro raggiungono la lunghezza di alcuni metri e un diametro di una frazione di metro. Il laser a He-Ne è lungo, generalmente, uno o più metri e ha un diametro di alcuni centimetri. I laser a CO2 di grande potenza raggiungono la lunghezza di alcune centinaia di metri e richiedono sistemi di pompaggio particolarmente sofisticati.
c) Descrizione qualitativa del processo laser. Condizione laser
Gli atomi laser-attivi sono eccitati dalla pompa esterna e cominciano a emettere luce spontaneamente. Il numero di fotoni emessi spontaneamente aumenta per effetto dell'emissione stimolata; d'altra parte una frazione dei fotoni è assorbita dagli atomi che si trovano nello stato fondamentale, mentre altri sfuggono attraverso gli specchi o sono diffusi da imperfezioni, ecc. L'effetto laser può verificarsi solo se il tasso di perdita dei fotoni è almeno bilanciato dal tasso di creazione. Questo fatto conduce alla ‛condizione laser' di Schawlow e Townes (v., 1958). Sia τ la vita media radiativa di un atomo, che emette 1/τ fotoni al seéondo spontaneamente. In generale, entro la larghezza di una riga di emissione atomica vi è ancora un grande numero p di modi nei quali la luce può essere emessa. Poiché consideriamo solamente la generazione di un unico tipo di fotoni (con data frequenza, direzione di propagazione e polarizzazione), dobbiamo dividere il tasso di transizione 1/π per il numero p. Secondo la relazione di Einstein, il tasso di emissione stimolata per atomi eccitati è n/(τp), dove n è il numero di fotoni presenti. Se vi sono N2 atomi nello stato eccitato da cui ha inizio l'emissione stimolata ed N1 nello stato inferiore che assorbe, il tasso totale di creazione di fotoni è dato da (N2−N1)n/(πp). Se indichiamo con t0 la vita media di un fotone nella cavità, il tasso di perdita è n/t0. L'effetto laser s'inizia se il guadagno netto è più grande della perdita e quindi se
Nel caso in cui la forma della riga sia lorentziana, p è dato da 4πν2V Δν/c3, dove V è il volume della cavità, c è la velocità della luce nel mezzo e Δν la larghezza ottica della riga di emissione. La condizione laser sarà quindi (con ω=2πν)
Affinché la condizione laser sia soddisfatta, la vita media t0 di un fotone nella cavità deve essere sufficientemente lunga. Si può pensare che la vita media di un fotone sia
dove R è la riflettività degli specchi ed L è la lunghezza del laser. Inoltre la larghezza della riga Δν deve essere piccola e il fattore (N2−N1) (chiamato ‛inversione') sufficientemente grande. L'effetto laser fu rivelato per la prima volta da Maiman in cristalli di rubino (v. Maiman, 1960).
d) Caratteristiche principali della luce laser
Le caratteristiche principali della luce laser sono la coerenza spaziale (direzionalità), la coerenza temporale (purezza spettrale), l'alta stabilità dell'ampiezza (basso rumore), l'alta intensità e la possibilità di creare impulsi di luce cortissimi (v. Haken, 1970).
Coerenza spaziale. - Un'onda luminosa che si propaghi in una certa direzione può essere rappresentata, con buona approssimazione, da un'onda piana. Qualora si praticassero due fenditure su uno dei due specchi, la distribuzione del campo a distanza sarebbe eguale a quella prodotta per interferenza in zona di Fraunhofer da un'onda piana passante attraverso due fenditure. Il fascio che esce dagli specchi terminali è altamente direzionale, poiché la sua divergenza si avvicina al limite teorico imposto solamente dalle leggi della diffrazione, dato da λ/d (dove λ è la lunghezza d'onda e d il diametro degli specchi).
Coerenza temporale. - La larghezza della riga laser è data, come vedremo più avanti, dalla formula (58). Sono stati osservati valori sperimentali dell'ordine di parecchi hertz, mentre il limite teorico non si riesce a raggiungere a causa di perturbazioni esterne, come per esempio le fluttuazioni degli specchi, le lente variazioni dell'intensità della pompa, ecc.
Fluttuazioni di bassa intensità. - La luce laser ha un'ampiezza molto stabile, cui sono sovrapposte piccole fluttuazioni, e una lenta variazione della fase (v. formula 50). Al contrario, la luce prodotta da sorgenti termiche consiste di una sovrapposizione casuale di pacchetti d'onda finiti con fasi scorrelate.
Alta intensità. - Nel funzionamento in continua sono state raggiunte intensità maggiori di 105 watt, mentre, con impulsi brevissimi, si sono superati i 1012 watt. Questi valori sono comunque in continuo aumento e anzi, date le possibili applicazioni militari, probabilmente i dati più aggiornati non sono pubblicati. Poiché le distribuzioni dei campi sono quelle proprie di onde piane, è possibile ottenere un alto focheggiamento e quindi un'intensità del campo pari a 108 V/cm e forse più.
Impulsi ultracorti. - La luce laser può essere emessa in impulsi brevissimi della durata di 10-13 secondi, ma si possono ottenere tempi ancora più corti. Le potenze raggiungono i 1012 watt o più.
e) La teoria del laser
La teoria del laser (v. Haken, 1970) può essere discussa servendosi delle equazioni di evoluzione temporale, di quelle semiclassiche e di quelle quantistiche. In termini generali, le ‛equazioni evolutive' permettono di determinare le caratteristiche principali della luce laser, cioè la condizione laser, l'intensità della luce in funzione della potenza della pompa, la coesistenza dei modi, le oscillazioni di rilassamento, ecc. Le ‛equazioni semiclassiche' permettono inoltre di determinare le frequenze e le fasi della luce laser emessa; permettono di trattare gli effetti del cosiddetto ‛bloccaggio dei modi', gli effetti di modulazione, la dipendenza temporale delle variazioni della popolazione e gli impulsi ultracorti. Le ‛equazioni quantistiche' sono necessarie per derivare le proprietà di coerenza della luce laser, in particolare per determinare la larghezza della riga e le proprietà statistiche dei fotoni. Inoltre, usando opportune approssimazioni, è possibile dedurre le equazioni semiclassiche e le equazioni del moto dalle equazioni quantistiche.
Le equazioni evolutive. - Le equazioni evolutive furono utilizzate per la prima volta da Einstein (v., 1917) e successivamente furono applicate da H. Statz e G. A. de Mars alla teoria del maser (v. Statz e de Mars, 1960).
Esse descrivono la variazione temporale del numero di fotoni di uno o più modi per effetto dell'emissione spontanea, dell'emissione stimolata, dell'assorbimento e delle perdite. Una descrizione completa comprende anche le equazioni riguardanti la variazione dei numeri di occupazione atomica. L'esempio più semplice è quello in cui vi sia un numero n di fotoni di un dato tipo nel risonatore e un numero N di atomi laser-attivi. Consideriamo, per fissare le idee, lo schema di pompaggio rappresentato nella fig. 4, in cui vi è un rilassamento rapido dal livello 3 al livello 2, cosi che in pratica si ottiene un pompaggio diretto dal livello 1 al livello 2. La variazione temporale del numero n di fotoni è data dal tasso di emissione spontanea N2/τ, più il tasso di emissione stimolata diminuito del tasso di assorbimento (N2−N1)n/(τp), più il tasso di perdita −2κn, dove 2κ=1/t0. L'equazione per la variazione temporale del numero di fotoni sarà quindi data da
dove
La variazione, causata dal processo laser e dal pompaggio, dei numeri totali di occupazione, N1 ed N2, rispettivamente del livello inferiore e superiore degli atomi, è data da
dove w21 è la velocità di pompaggio dal livello 1 al livello 2 dovuto alla pompa esterna e w12 è la velocità di transizione dal livello 2 al livello I dovuta a processi incoerenti (cioè nonlasing), come l'emissione spontanea in altri modi, o a transizioni non radiative ecc. La condizione laser può essere derivata anche dall'equazione (1); se la condizione laser è soddisfatta, il numero di fotoni nello stato stazionario è dato da
dove
In questa derivazione si è trascurato l'effetto dell'emissione spontanea. Se per effetto di qualche condizione iniziale il numero di fotoni differisce in maniera sensibile dal valore per lo stato stazionario dato dalla (5), si producono delle ‛oscillazioni di rilassamento'. Le equazioni di evoluzione descrivono il funzionamento di un cosiddetto laser Q-swiiched. L'inverso della costante di perdita, 1/κ, è proporzionale al fattore di merito Q.
In un laser Q-switched all'inizio gli specchi sono molto trasparenti, hanno cioè un basso Q, che impedisce l'azione laser: in questo modo con la pompa si può raggiungere una alta inversione N2−N1. Poi, in un tempo brevissimo, il fattore Q viene aumentato (il potere riflettente delle facce estreme viene improvvisamente aumentato) in modo tale che la condizione laser viene improvvisamente soddisfatta. Il numero n di fotoni aumenta quindi molto rapidamente. La larghezza dell'impulso è dell'ordine del nanosecondo (10-9 s).
Le equazioni di evoluzione sono anche state formulate e risolte per diversi altri modi del campo e per altri schemi di pompaggio e di transizione.
La teoria semiclassica. - La teoria semiclassica del laser tratta il campo della luce laser come un campo classico di radiazione. Gli atomi sono trattati quantisticamente mediante l'assegnazione di opportuni valori di aspettazione dei momenti atomici di dipolo e del numero di occupazione atomica. Questa teoria è stata sviluppata indipendentemente da Haken e collaboratori (v. Haken, 1962 e 1970; v. i contributi di Haken e Sauermann, 1963), per i laser a stato solido, i laser a semiconduttori e i laser a gas, e da Lamb e collaboratori (v. Lamb, 1964; v. Sargent III e altri, 1974), per i laser a gas. Secondo questa teoria, il campo della luce laser è descritto dal campo elettrico che obbedisce all'equazione delle onde (derivata dalle equazioni di Maxwell):
In questa formula e in quelle successive il punto indica la derivazione rispetto al tempo, c la velocità della luce nel mezzo inattivo, σ è la conducibilità (per es. degli specchi agli estremi), P la polarizzazione del mezzo attivo. Se quest'ultimo è formato da atomi singoli, P può essere decomposto nella somma del momento di dipolo pμ dei singoli atomi, di indice μ, ciascuno moltiplicato per una funzione molto localizzata (funzione δ):
I momenti di dipolo pμ obbediscono all'equazione
dove νμ indica la frequenza dell'oscillatore atomico (frequenza di transizione dell'elettrone tra il livello 1 e il livello 2), γ la costante di smorzamento (che corrisponde a T2-1 nella risonanza magnetica), ω0 la frequenza di ciascun modo del campo (v. sotto), E(xμ) l'intensità del campo nel punto xμ per l'atomo μ, dμ l'inversione dell'atomo a due livelli, dμ=(N2−N1)μ, e ϑ12 il cosiddetto elemento della matrice di dipolo ottenuto con i metodi della meccanica quantistica. L'inversione dμ soddisfa l'equazione
dove d0 indica l'inversione causata dal pompaggio esterno e da transizioni non laseranti e T il tempo di rilassamento dell'inversione atomica (che corrisponde a T1 nella risonanza magnetica).
Le equazioni del laser (9) e (10) non sono lineari. Moltiplicando l'equazione (9) per δ(x−xμ) e sommando su μ, si ottiene per il momento di polarizzazione P l'equazione
In questa formula si è supposto che sia νμ=ν, cioè che non vi sia allargamento non uniforme e d(x) è definito da
cioè è l'inversione atomica per unità di volume. In modo simile, l'equazione (10) può essere trasformata nella
Le equazioni (7), (11) e (13) possono essere usate per discutere l'azione laser e i fenomeni di propagazione ondosa con atomi laser-attivi in posizioni fisse.
Semplificazione delle equazioni laser nel modello ondulatorio. - Consideriamo un caso particolarmente importante e cioè quello in cui si suppone che la riga sia uniformemente allargata e quindi che tutte le frequenze di transizione siano uguali, νμ≡ν, si suppone inoltre che vi sia una risonanza esatta tra i modi del campo con frequenza ω0 e la frequenza atomica. Il modulo del campo elettrico E propagantesi in direzione x con frequenza ω0 sarà dato dall'espressione
E(x, t)=E(-)(x, t) exp(iω0t−ik0x)+c.c., (14)
dove poniamo
ω0=ck0. (15)
Se supponiamo che l'ampiezza E vari lentamente, il termine ∂E/∂t può essere trascurato rispetto ω0E. Se inoltre trascuriamo i termini rapidamente oscillanti del tipo exp(2iω0t), piccoli rispetto all'unità, otteniamo: 1) l'equazione per la intensità del campo (supponendo che sia fissata la direzione di polarizzazione)
2) l'equazione per la polarizzazione
3) l'equazione per l'inversione
nelle quali P(-) è definito da una relazione simile alla (14). Le grandezze col segno positivo rappresentano le complesse coniugate di quelle col segno negativo e infine D0=Nd0 è l'inversione totale fissata. Per piccoli valori di D0 non si ha effetto laser, cioè
E(-)=P(-)=0
D=D0, (19)
mentre se D0 è compreso tra due valori critici dell'inversione, Dc1 e Dc2 allora E(-) e P(-) assumono valore costante non nullo. Per
D0〈 Dc2 (20)
l'onda continua si spezza in una serie di impulsi molto corti, che possono essere sia regolari (se κ>γ+γ11) sia irregolari o ‛turbolenti' (se κ〈γ+γ11) In pratica si generano impulsi molto corti quando c'è un aggancio attivo dei modi (ottenuto per es. modulando l'assorbimento degli specchi) o ancor più efficacemente quando c'è un aggancio passivo, ottenuto usando assorbitori saturabili (v. sotto).
Le equazioni laser per i moduli normali. - Nell'impostazione ‛modale' dell'equazione del campo è spesso conveniente decomporre l'intensità di questo secondo i modi normali della cavità (nel caso più semplice onde piane), cioè porre:
Ciascun modo obbedisce all'equazione
DUλ(x)=-k2λUλ, (22)
dove si è posto
e ωλ è la frequenza del modo nel risonatore vuoto.
Supporremo che i modi normali, che indichiamo con l'indice λ, siano fra loro ortogonali. Poniamo
con
e introduciamo inoltre le grandezze adimensionali bλ e αμ, definite da
con le loro complesse coniugate corrispondenti. Poniamo inoltre
In unità adimensionali, l'ampiezza del campo bλ, il momento di dipolo atomico αμ e l'inversione atomica dμ, oddisfano le seguenti equazioni:
dove
dμ=(N2−N1)μ. (32)
L'equazione (29) descrive la variazione temporale dell'ampiezza del modo bλ causata dalle oscillazioni libere (ωλ), dalle perdite della cavità (−κλ), che possono dipendere dal modo λ, e dal momento di dipolo αμ. L'equazione (30) descrive la variazione temporale del momento di dipolo αμ dovuta alle oscillazioni libere (νλ), ai processi che producono sfasamenti (γ) e ai processi di assorbimento o di emissione stimolata (Σλ), L'equazione (31) descrive la variazione temporale dell'inversione dμ dovuta alla pompa (d0/T), al rilassamento (−dμ/T) e all'emissione stimolata e all'assorbimento (ultimi termini). Le equazioni (29), (30) e (31) costituiscono la base per lo studio di numerosi problemi riguardanti il funzionamento a uno o più modi di atomi a due livelli (si possono scrivere equazioni corrispondenti per atomi con molti livelli; v. Haken, 1970). Per risolvere le (29), (30) e (31) si pone, nella maggior parte dei casi,
bλ(t)=Bλ(t) exp(iΩλt), (33)
in cui Bλ e Ωλ sono determinati in base a un procedimento di autocompatibilità. Nel caso in cui sia κ≪γ11>γ, le variabili atomiche αμ e dμ possono essere eliminate ‛adiabaticamente' (v. Haken, 1962; v. i contributi di Haken e Sauermann, 1963; v. Lamb, 1964). All'ordine più basso non nullo le bλ soddisfano l'equazione
dove G e C sono funzioni di Ωλ e delle costanti del processo laser. Risolvere l'equazione (34) è in generale ancora molto complicato, così che qui ci limiteremo a ricordare alcuni importanti risultati. 1) Teoria a modo singolo. Se la riga atomica è uniformemente allargata, la soluzione stazionaria è data dall'equazione (5), dove
b*b=n (35)
e la variazione di frequenza è data dalla formula di Townes:
Nel caso di righe non uniformemente allargate la variazione di frequenza Ω−ω dipende dal numero n di fotoni. 2) Teoria a modi multipli. Se la riga è uniformemente allargata e se vi sono soltanto modi corrispondenti a onde progressive, cioè se Uλ∝exp(ikλx), con una sola direzione di polarizzazione, può sostenersi soltanto il modo per il quale si ha il più alto guadagno e la perdita più bassa. Se invece la riga non è uniformemente allargata (cioè se νμ dipende da μ, come si dirà più avanti) e/o la cavità permette l'esistenza di onde stazionarie, diventa allora possibile la coesistenza di modi. In generale, le variazioni di frequenza dipendono dalla potenza e inoltre si può verificare un aggancio in frequenza, cioè, per esempio, le frequenze di tre modi successivi possono obbedire alla relazione Ω3−Ω2=Ω2−Ω1, indipendentemente dalla presenza di eventuali altri slittamenti di frequenza. L'aggancio in frequenza può essere esaltato dalla modulazione delle perdite, cioè variando la costante di assorbimento κ con una frequenza ω′ prossima alla differenza fra le frequenze dei modi del risonatore ‛carico'. L'ampiezza totale del campo elettrico è quindi data da
Se supponiamo che sia Em=E0, per m=−(m0−1)/2, ..., (m0−1)/2, ed Em=0 negli altri casi, si può allora eseguire la somma, che dà come risultato
L'intensità totale I=∣E∣2 è data da
e l'intensità massima da
Iagg=∣E0∣2 m²0,
cioè è proporzionale al quadrato del numero m0 di modi agganciati. Senza questo aggancio, e cioè quando le fasi sono scorrelate, l'intensità è proporzionale al solo m0.
La larghezza τ dell'impulso è data da
ed è quindi inversamente proporzionale all'intervallo di frequenza Δω=ω′m0, che è dell'ordine della larghezza della riga atomica.
Impulsi molto corti possono essere generati nella maniera più efficace per mezzo di un assorbitore saturabile (colorante) posto fra il materiale laser-attivo e uno degli specchi. Un assorbitore saturabile assorbe luce di bassa intensità e diventa trasparente ad alte intensità e perciò taglia le code di bassa intensità degli impulsi in via di sviluppo. Poiché, d'altro canto, gli impulsi attraversano il mezzo attivo più volte, essi diventano sempre più corti e più intensi.
Teoria quantistica del laser. - La teoria quantistica del laser è stata sviluppata da Haken e collaboratori e, successivamente, da Lamb, Lax e altri (v. Haken, 1964 e 1970; v. Hempstead e Lax, 1967; v. Sargent III e altri, 1974). In una trattazione interamente quantomeccanica del laser, il campo elettromagnetico viene descritto per mezzo dell'elettrodinamica quantistica e gli elettroni degli atomi per mezzo di operatori di creazione e di annichilazione di elettroni negli stati j=1, 2, ... dell'atomo μ. Generalmente si parte da una hamiltoniana comprendente l'hamiltoniana degli elettroni, quella dei modi del campo e quella delle interazioni tra i due sistemi. L'effetto dovuto ad altri fenomeni, come la pompa, le perdite, i processi di decadimento incoerente ecc., è descritto per mezzo di serbatoi, rappresentati da altre hamiltoniane. Si comincia con l'eliminare le variabili che descrivono i serbatoi; in tal modo, se si utilizza per questo procedimento la rappresentazione di Schrödinger, si ottiene un'equazione per la matrice densità. Se invece si usa la rappresentazione di Heisenberg, nella quale gli operatori Ω sono dipendenti dal tempo e soddisfano l'equazione
si ottengono le cosiddette equazioni quantomeccaniche di Langevin. I serbatoi generano forze di smorzamento e di fluttuazione. Formalmente le equazioni quantomeccaniche di Langevin coincidono con le equazioni semiclassiche (29), (30) e (31) se ad esse si aggiungono certe forze oscillanti F. In questo caso bλ e b*λ vanno interpretati come operatori di annichilazione e di creazione che obbediscono alle relazioni di commutazione
I momenti di dipolo adimensionali devono essere sostituiti secondo lo schema seguente:
dove a+jμ, ajμ sono rispettivamente operatori di creazione e di annichilazione di un elettrone nel livello j dell'atomo μ. Le equazioni del campo sono quindi
in modo analogo le equazioni (30) e (31) si trasformano in equazioni quantomeccaniche. Anche in questo caso si possono eliminare adiabaticamente gli operatori atomici. Se si considera un unico modo, l'equazione approssimata dell'oscillatore di van der Pol diviene
b•=(G−κ)b−C∣b∣2 b+F(t), (44)
nella quale G indica il cosiddetto ‛guadagno non saturato' dato da
e C è definito da
In queste equazioni si è supposto che l'allargamento della riga sia uniforme e che si abbia perfetta risonanza. Il significato dell'equazione (44) appare chiaro se per un momento si considera b come un numero complesso e lo si interpreta come coordinata q di una particella. Invero l'equazione (44) è un caso particolare, per m molto piccolo, della
mq¨+ó=K(q)+F(t), (47)
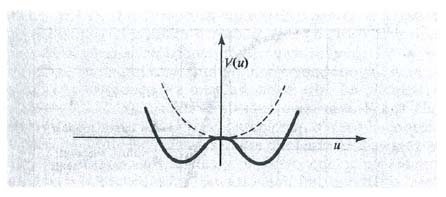
la quale descrive il moto di una particella soggetta a una forza K in un campo di potenziale V:
Il grafico del potenziale V=(κ−G)q2/2+Cq4/4 è riportato nella fig. 21. Per G>κ avremo equilibrio per q=0 e la particella oscillerà attorno alla posizione di equilibrio sotto l'azione della forza F(t). Se immaginiamo che la forza F(t) sia dovuta all'emissione spontanea di fotoni, dopo ogni atto di emissione (che imprime un impulso alla particella) l'ampiezza b (cioè la coordinata della particella q) tenderà ad annullarsi. Poiché F(t) consiste di una serie di impulsi casuali, l'ampiezza b del campo è una sovrapposizione di pacchetti d'onda scorrelati che decadono nel tempo. Il valore medio si annulla:
〈b>=0. (49)
Nel caso in cui sia G〈κ, sono possibili nuovi stati stabili. Poiché il potenziale V dipende solo dal modulo di b, il problema è a simmetria sferica e, siccome non vi sono forze di richiamo in direzione tangenziale alla buca di potenziale, la ‛particella fittizia' è sottoposta a un processo di diffusione nella direzione tangenziale sotto l'influenza delle forze scorrelate. Il moto in direzione assiale è invece molto stabile. Da queste considerazioni è possibile derivare (v. Haken, 1964) la forma generale dell'ampiezza
b=[r0+ρ(t)] exp[iϕ(t)], (50)
nella quale r0 indica un'ampiezza stabile, ρ(t) l'ampiezza delle fluttuazioni e la fase ϕ(t) descrive il processo di diffusione. La forma (50) di b rimane valida anche quando b è un operatore. In questo caso r0 è ancora un numero complesso, mentre ρ e ϕ rappresentano opportuni operatori.
Corrispondenza tra le trattazioni quantistica e classica ed equazione di Fokker-Planck. - Il ‛principio di corrispondenza' permette di trasformare le equazioni e gli operatori quantomeccanici in equazioni e variabili classiche, secondo procedimenti ben definiti. Le equazioni classiche contengono le stesse informazioni fisiche delle corrispondenti equazioni quantomeccaniche. Per un numero sufficientemente grande di fotoni (dell'ordine di 102) le equazioni classiche possono essere notevolmente semplificate. Per esempio, l'equazione (44) può essere trasformata in un'equazione classica della stessa forma. All'equazione di Langevin può essere associata un'equazione di Fokker-Planck, che descrive la variazione temporale della distribuzione di probabilità W dell'ampiezza del campo. Passando in coordinate polari, secondo la relazione b→r exp(−iϕ), l'equazione di Fokker-Planck per W(r, ϕ) diviene
dove ò è il numero medio di fotoni e
In quest'ultima espressione nth è il numero dei fotoni termici (che è importante nel maser ma non nel laser) e nsp è il numero dei fotoni emessi spontaneamente, dato da
dove N2s è il numero di atomi nel livello superiore (numero di occupazione saturato) e il denominatore è l'inversione alla soglia.
La soluzione stazionaria dell'equazione (51) è (v. Risken, 1965; v. Hempstead e Lax, 1967)
W(r)=N exp(α1r2−α2r4), (56)
dove si ponga
Alla soglia laser la funzione di distribuzione cambia qualitativamente e la misura diretta del numero dei fotoni (v. Arecchi e Degiorgio, 1972; v. Pike, 1970) è in eccellente accordo con la teoria.
Le soluzioni dipendenti dal tempo dell'equazione (51), che sono necessarie per determinare l'ampiezza della riga e i tempi di rilassamento, possono essere calcolate solamente ricorrendo a un elaboratore.
Larghezza della riga ottica, funzioni di correlazione e statistica dei fotoni. - La larghezza Δω della riga ottica può essere definita per mezzo della funzione di correlazione fra le ampiezze (per es. v. Mandel e Wolf, 1970)
〈E(-)(τ)E(+)(0)>=〈E(-)(0)E(+)(0)> exp(−Δωτ). (58)
Ben al di sopra della soglia laser, l'espressione di Δω è data da (v. Haken, 1970)
dove ω è la frequenza del laser, P=2κ〈n>ℏω la potenza emessa, 〈n> il numero medio di fotoni, Δ=(ν0−ω)/(κ+γ) è proporzionale alla differenza fra la frequenza del modo ω e la frequenza della transizione atomica ν0. L'equazione (59) si applica alle transizioni uniformemente allargate. Nel caso in cui le righe non siano uniformemente allargate e nel caso dei laser a gas è necessario aggiungere dei fattori di correzione. Le larghezze delle righe al di sotto e al di sopra della soglia sono legate dalla formula:
Δω(a)P(0)=α(a) Δωsopra Psopra, (60)
dove a è un parametro che descrive la potenza della pompa e α è una funzione che varia con continuità dal livello 1 al di sotto della soglia al livello 2 al di sopra della soglia.
La funzione di correlazione per il numero di fotoni misurato al tempo t e al tempo t+τ (esperimento di Hanbury-Twiss) è definita dalla (v. Glauber, 1963)
Γ(τ)=〈b+(t)b+(t+τ)b(t+τ)b(t)>−〈b+b>〈b+b>. (61)
Al di sotto della soglia la formula si riduce a
Γ(τ)=〈b+b>2 exp(−2 Δωτ), (62)
dove si è indicata con Δω la larghezza della riga ottica. In prossimità della soglia, la formula (61) si riduce a una sovrapposizione di curve lorentziane della forma (v. Risken e Vollmer, 1967)
La formula (63) può essere sostituita, con buona approssimazione, da un'unica curva di Lorentz con un'opportuna larghezza effettiva. Un po' al di sopra della soglia l'equazione (61) può essere scritta nella forma
dove
Γ(0) è indipendente dalla potenza della pompa, in conseguenza del fatto che la luce laser ha un'ampiezza molto stabile al di sopra della soglia. Le profonde differenze fra le proprietà statistiche della luce al di sopra e al di sotto della soglia furono per la prima volta previste in un lavoro di H. Haken (v., 1964). La soluzione stazionaria (55) permette di derivare la statistica dei fotoni. Indicando le medie statistiche col simbolo 〈 >, possiamo scrivere in tutta generalità
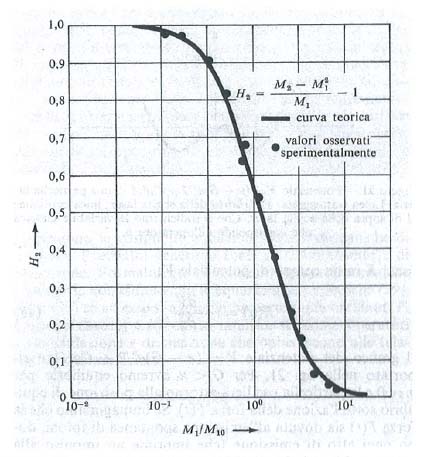
〈n2>−〈n>2=〈n>(1+H2〈n>), 66)
dove H2 è definita da questa equazione. Per valori al di sotto della soglia si ottiene l'espressione
〈(Δn)2>=〈n>(〈n>+1), (67)
caratteristica della statistica di Bose-Einstein; per valori leggermente al di sopra della soglia si ottiene invece
〈(Δn)2>=〈n>, (68)
caratteristica della distribuzione di Poisson. La transizione graduale tra le due regioni è rappresentata nella fig. 23, che mostra un ottimo accordo fra i valori sperimentali (v. Arecchi e altri, 1967) e la curva teorica (v. Risken e Vollmer, 1967).
Relazioni fra equazioni quantomeccaniche, semiclassiche ed evolutive. - Se si prendono i valori di aspettazione e i valori medi statistici delle equazioni quantomeccaniche, si ottengono le equazioni semiclassiche, pur di sostituire le medie dei prodotti coi prodotti delle medie, cioè, per esempio, 〈bλαμ > con 〈bλ >〈αμ >. Se nelle equazioni semiclassiche così ottenute si eliminano ‛adiabaticamente' i momenti di dipolo e si mediano le fasi nelle equazioni risultanti trascurando l'aggancio in fase, si ottengono le equazioni del moto.
Analogia tra un laser e una transizione di fase. - Alla soglia laser il comportamento della luce varia qualitativamente. Da un insieme di pacchetti d'onda scorrelati emessi al di sotto della soglia si passa a un'onda coerente al di sopra della soglia; l'emissione di luce subisce un'improvvisa discontinuità alla soglia laser e le fluttuazioni dell'intensità diminuiscono rapidamente al di sopra della soglia.
Sussiste la seguente analogia con una transizione di fase di sistemi in equilibrio termico (v. Haken, 1970; v. Graham e Haken, 1968; v. Degiorgio e Scully, 1970): il potenziale V(∣b∣) (v. formula 48) corrisponde all'energia libera F di un sistema in equilibrio termico. La funzione di distribuzione (51) è analoga a quella di un sistema in equilibrio termico in una transizione di fase del secondo ordine nella teoria di Landau. Per G=κ si verifica un'instabilità che rompe la simmetria; per G>κ esiste un solo stato di equilibrio stabile, con ∣b∣=0, che non privilegia alcuna direzione (fase), mentre per G〈κ le posizioni di equilibrio stabile corrispondono a b=r0 exp(iϕ0)≠0, dove ϕ0 è una fase arbitraria. La simmetria sarà poi ripristinata dalla diffusione della fase. Per G che tende a κ da valori di G>κ, l'ampiezza, ovvero la coordinata della particella, rilassa sempre più lentamente e cioè si ha uno smorzamento critico, connesso con il cosiddetto soft mode. L'analogia fra transizione di fase ed effetto laser è valida anche nel caso di modi continui. In questo caso avremo una completa analogia con la teoria della superconduttività di Ginzburg-Landau (v. Haken, 1970; v. Graham e Haken, 1968). Il laser ha consentito per la prima volta di individuare e di studiare in dettaglio l'analogia tra la transizione di fase di un sistema non in equilibrio e quella di un sistema in equilibrio.
Il laser come sistema sinergetico. - Il laser si presta anche come eccellente modello per processi autoorganizzanti, che includono i sistemi biologici. Oli atomi, che al di sotto della soglia laser emettono pacchetti d'onda individualmente, al di sopra della soglia cominciano improvvisamente a oscillare in modo coerente. Sembra quindi che un qualche ‛demone' imponga agli atomi di agire in una maniera ben regolata. Questi problemi attualmente sono trattati dalla ‛sinergetica' (v. Haken, 1977), scienza interdisciplinare che studia la coordinazione tra vari sottosistemi che dà luogo a condizioni d'ordine a livello macroscopico. Esistono anche dei legami tra la teoria semiclassica del laser e la teoria matematica delle biforcazioni.
3. Ottica non lineare
a) Analogia tra atomi a due livelli e particelle a spin 1/2
La meccanica quantistica di un elettrone atomico che può occupare solo due livelli è completamente analoga alla teoria quantistica di una particella a spin 1/2 (v. Feynmann e altri, 1957; v. Allen ed Eberly, 1975; v. Haken, 1970).
Sotto l'azione di due campi magnetici perpendicolari, uno costante e l'altro alternato, lo spin si comporta come un giroscopio e passa dal suo stato inferiore a quello superiore. Se il campo magnetico alternato viene applicato per un tempo tale che lo spin ruoti di 90° rispetto al campo magnetico costante, si parla di un impulso di π/2 o di 90°; si definisce analogamente un impulso di 180° o di π. In maniera simile, inviando un'onda luminosa coerente in risonanza con la frequenza di transizione atomica fra due livelli di un atomo, si genera un momento di dipolo oscillante e l'elettrone passa dal livello inferiore a quello superiore. Di conseguenza si forma un pacchetto d'onde descritto da
ψ(x, t)=c1(t)ϕ1(x, t)+c2(t)ϕ2(x, t), (69)
dove con ϕj(x, t) indichiamo la funzione d'onda dipendente dal tempo t e dalla posizione x dello stato j dell'elettrone, in assenza di campo esterno. I coefficienti c1 e c2, dipendenti dal tempo, sono della forma c1(t)=cos ωft, c2=sen ωft, dove wf=ef/ℏ (e=carica dell'elettrone, f=intensità del campo). Questa analogia ci permette di trasferire i risultati sperimentali ricavati dallo studio del comportamento dello spin in campi magnetici al caso di atomi sotto l'azione di campi luminosi. Accenniamo ora ai più importanti risultati raggiunti.
Superradianza e superfluorescenza. - Applicando a un sistema atomico o a uno spin un impulso di 90°, esso decade con emissione coerente di un breve impulso luminoso (superradianza; v. Dike, 1954). Se invece si applica un impulso di 180°, viene emesso un breve lampo luminoso: questo fenomeno è chiamato ‛superfluorescenza' (v. Bonifacio e altri, 1971). Se N è il numero di atomi che intervengono nel processo, la durata dell'impulso è proporzionale a 1/N e l'intensità è proporzionale a N2 invece che a N, come nella fluorescenza normale.
Impulso di 2π, trasparenza autoindotta. - Applicare un impulso di 2π significa che il sistema atomico (spin) ritorna nelle condizioni iniziali dopo essere stato investito da un impulso o, in altre parole, che l'impulso luminoso è passato attraverso il sistema atomico. Si tratta di un fatto notevole, perché la frequenza centrale dell'impulso luminoso è in risonanza con la transizione atomica e quindi ci si potrebbe aspettare l'assorbimento dell'impulso. Questo fenomeno è possibile quando la durata dell'impulso è breve in confronto ai tempi di rilassamento del sistema atomico (v. MacCall e Hahn, 1969).
Foto-eco (spin-eco). - In questo caso prima si applica un impulso di 90° agli atomi (per es. a ioni di Cr nel rubino), che induce un grossissimo momento di dipolo oscillante che emette luce intensa. A causa dell'allargamento uniforme e non uniforme, i momenti di dipolo atomici individuali si sfasano di una quantità che può essere compensata applicando un impulso di 180°. In virtù degli effetti irreversibili dell'allargamento uniforme, l'impulso luminoso emesso in questo caso è meno intenso e ciò permette di misurare l'allargamento uniforme delle transizioni ottiche atomiche (v. Abella e altri, 1966).
b) Effetto Stark dinamico
Se un atomo a due livelli è sottoposto a un campo ottico coerente e risonante, a causa dell'emissione spontanea succede che lo spettro di emissione presenta, accanto alla riga centrale, due righe laterali (v. Carmichael e Walls, 1976).
c) Bistabilità ottica
Supponiamo che un'onda luminosa continua, coerente e in risonanza attraversi una cavità laser in direzione assiale entrando da uno dei due specchi semitrasparenti. Se il materiale laser-attivo non è pompato, la luce incidente è assorbita se ha bassa intensità ed è invece trasmessa attraverso il risonatore se ha alta intensità. Per intensità della luce incidente compresa entro un certo intervallo di valori, possono aver luogo ambedue i processi, a seconda delle condizioni iniziali: ciò significa che si hanno effetti di bistabilità o di isteresi (v. Szöke e altri, 1969; v. Bonifacio e altri, 1971).
d) Interazioni non lineari delle onde
Mescolamento di frequenze. - L'ottica non lineare in senso stretto tratta quei fenomeni di propagazione ondosa in cui il momento di polarizzazione P della materia, che interviene nell'equazione (7), dipende in maniera non lineare dall'intensità del campo elettrico:
I tensori χ del primo, secondo, terzo, ... ordine sono i tensori della suscettività elettrica. L'intensità E del campo della luce prodotta da normali lampade è in generale così piccola, che i termini non lineari della (70) possono essere trascurati. Tuttavia, l'alta intensità del campo della luce emessa da un laser porta a fenomeni non lineari che sono misurabili. Le proprietà di χ dipendono dalle simmetrie del mezzo materiale. Se per esempio il cristallo è centrosimmetrico (cioè gli atomi del cristallo vengono semplicemente scambiati se si sostituiscono le coordinate x, y, z rispettivamente con −x, −y, −z, misurate rispetto a un'opportuna origine) χ(2) annulla. Considerazioni di simmetria ci permettono di dedurre una serie di relazioni fra i vari χ.
Per illustrare il significato fisico dell'equazione (70), consideriamo per esempio il termine χ(2) e supponiamo che il vettore E=Elaser della (70) sia della forma (0, 0, E), con
E=E1 exp(ik1x−iω1t)+E2 exp(ik2x−iω2t)+c.c. (71)
Sfruttando l'invarianza per traslazioni di χ(j) nei cristalli, otteniamo per la parte di P che dipende da χ(2) in una certa direzione:
P(2)(x, t)=χ(k²1),k2E1E2 exp[i(k1+k2)x−i(ω1+ω2)t] (72)
+ altre combinazioni delle k e delle ω.
Poiché P compare come un termine di sorgente nell'equazione delle onde (7), oltre alle frequenze ω1 e ω2 compariranno nuove combinazioni di frequenze: ω=∣ω1±ω2∣. Se ω1=ω2 e se ω=2ω1, si verificherà la produzione di ‛seconde armoniche'; se invece ω=ω1−ω2=0, si avrà l'effetto di ‛rettificazione ottica'. Si verificherà l'amplificazione ottica di un'onda di vettore d'onda k e frequenza ω solo se ω=ω1±ω2 e k=k1±k2. A causa della dispersione, questa condizione è soddisfatta solo sotto certe condizioni (quando c'è adattamento di fase), per esempio usando il raggio ordinario e quello straordinario in un cristallo di LiNbO3. Quando χ(2) si annulla a causa delle condizioni di simmetria, il termine χ(3) comporta un mescolamento di frequenze con ω=±ω1±ω2±ω3 (se consideriamo tre onde incidenti). È da notare che alcune delle ωj possono coincidere. Sono stati osservati e trattati teoricamente effetti di ordine ancora più alto (v. Bloembergen, 1965).
Diffusione stimolata di Raman e Brillouin. - Si verificano processi stimolati quando il campo laser incidente è accoppiato ad altri gradi di libertà del sistema, per esempio a quelli elettronici o vibrazionali. In questo caso la polarizzazione P dipende non solo dall'intensità del campo E (laser), ma anche dalle coordinate degli elettroni o degli atomi. Esempi tipici sono i seguenti. Un fotone con energia ℏω1 è assorbito dal sistema e successivamente viene emesso un fotone con energia ℏω2 ed eccitato un quanto vibrazionale con energia ℏωR, per i quali
ℏω1=ℏω2+ℏωR,
dove ω2>ω1. La riga di emissione originale è spostata verso frequenze più basse (‛riga di Stokes'): questo effetto è detto effetto (vibrazionale) di Raman (o diffusione di Raman). Se è invece ℏω1=ℏω2+ℏωR, viene assorbito un quanto vibrazionale e ω2〈ω1 (‛riga anti-Stokes'). Quando l'energia ℏωR proviene da una transizione atomica, si parla di effetto Raman elettronico. Quando ℏωR proviene da una vibrazione del reticolo, si parla di ‛diffusione di Brilbuin'. Quando è ℏω1=Ea−Eb (con Ea, Eb livelli reali di energia del sistema), l'effetto di Raman (Brillouin) è detto risonante. In generale, però, è ℏω1≠Ea−Eb e l'assorbimento e l'emissione di fotoni avvengono tramite transizioni ‛virtuali' (v. atomo).
Si verifica ‛diffusione stimolata' di Raman (o di Brilbuin) se i fotoni con energia ℏω2 sono creati coerentemente per mezzo di emissione stimolata. La diffusione stimolata di Raman svolge un ruolo importante nella spettroscopia dei livelli energetici molecolari, in modo particolare attraverso il Coherent Anti-Stokes Raman Scattering (CARS), e dei tempi di rilassamento (v. Bloembergen, 1965).
Autofocalizzazione. - Un altro fenomeno precipuo della propagazione non lineare della luce è l'autofocalizzazione, in cui il diametro di un intenso raggio di luce si contrae nel passare attraverso un mezzo non lineare.
e) Assorbimento di due o più fotoni
A causa della sua alta intensità, una radiazione laser di frequenza ω può portare un elettrone da uno stato legato di un atomo, molecola o solido (semiconduttore) a uno stato eccitato per mezzo di n(≥2) fotoni, in modo tale che nℏω=Ea-Eb. Le transizioni hanno luogo attraverso i cosiddetti livelli virtuali, per i quali le leggi di conservazione dell'energia non sono soddisfatte.
f) Spettroscopia laser
La strettezza delle righe di emissione di un laser permette di eseguire misure di alta precisione.
Spettroscopia lineare (metodo di assorbimento per mezzo di misurazioni di transizione). - Si ottiene una rivelazione molto sensibile di righe di assorbimento deboli ponendo all'interno della cavità di un laser a più modi con una larga riga una sostanza che abbia un debole assorbimento nella banda di amplificazione del laser. La grande potenza e la direzionalità della luce laser permettono di eseguire la spettroscopia di oggetti distanti, per esempio di molecole sospese nell'aria. Questo è importante, per esempio, nel controllo dell'inquinamento.
Spettroscopia laser non lineare. - La spettroscopia laser non lineare, specificamente la ‛spettroscopia di saturazione' e la ‛spettroscopia a due fotoni', è di particolare importanza. In generale le misure di precisione delle righe spettrali di atomi e di gas sono limitate dall'allargamento della riga per effetto Doppler. Infatti, a causa del moto degli atomi del gas, vi è sempre una distribuzione della componente delle velocità rispetto a una qualsiasi direzione di osservazione, cosi che la frequenza della riga atomica è traslata a causa della velocità relativa dell'atomo rispetto all'osservatore e non si potrà in definitiva che osservare una riga allargata. La spettroscopia a eliminazione dell'effetto Doppler funziona nella maniera seguente: quando la luce laser interagisce con gli atomi del gas, questi vengono portati da un livello inferiore a un livello superiore, dove, a causa della condizione di risonanza, viene coinvolta solo una piccola frazione degli atomi, cioè quelli in risonanza con la luce laser. L'inversione di popolazione di questi atomi viene sensibilmente alterata e questo porta alla saturazione della loro riga di assorbimento. Sulla base di questo effetto di saturazione la posizione e la larghezza della riga di transizione atomica possono essere misurate con grande precisione. Un altro modo per ottenere misure di alta precisione si ha sfruttando l'assorbimento a due fotoni nelle righe allargate dall'effetto Doppler, nel quale i due fotoni, che saranno poi assorbiti, procedono in direzioni opposte eliminando cosi l'effetto di allargamento Doppler.
g) Ulteriori applicazioni fisiche della luce laser
L'alta intensità degli impulsi ultracorti del laser può essere usata per indurre la fusione nucleare. Gli impulsi di luce provenienti da numerosi laser scaricati contemporaneamente vengono fatti convergere su piccole sferette (di circa 1 mm di diametro), per esempio di tritio, per portarle a una temperatura sufficientemente alta da innescare i processi di fusione nucleare. I laser a neodimio-vetro e i laser a CO2 sembrano essere particolarmente adatti a questo scopo.
L'alta intensità e l'estrema strettezza delle righe di emissione laser permettono di eseguire la separazione degli isotopi. Si può, a tal fine, procedere nel modo seguente: una miscela di isotopi gassosi è irradiata da luce laser e, poiché la condizione di risonanza ottica è soddisfatta per un solo isotopo, questo viene eccitato, mentre gli altri rimangono nei loro stati fondamentali. La miscela viene poi irradiata con luce di un'altra frequenza in modo da ionizzare l'isotopo eccitato. Infine gli ioni possono essere deviati per mezzo di campi elettrici e magnetici incrociati e quindi possono essere isolati. Un metodo alternativo consiste nel deflettere gli atomi eccitati in un campo elettrico o magnetico non uniforme, in virtù del fatto che, quando un atomo viene eccitato, cambiano le sue proprietà elettriche e magnetiche.
Gli impulsi ultracorti del laser permettono di misurare tempi di rilassamento molto brevi (fino a 10-12 s) nei liquidi, nei gas e nei solidi e di verificare alcuni risultati dell'elettrodinamica quantistica.
Poiché la luce laser ha una frequenza molto alta rispetto alle onde radio, essa può trasportare in una banda piuttosto stretta molte più informazioni. Si sta ora sperimentando la trasmissione di luce laser modulata, prodotta da un laser a semiconduttore, lungo fibre di vetro. Si pensa pure a future applicazioni del laser, in particolare dei laser Nd-YAG, nelle comunicazioni spaziali. Brevi impulsi di luce laser, di circa 10-9 s, possono essere usati in un radar ottico, per rivelare e misurare la distanza di oggetti lontani.
Mediante la correlazione dei fotoni e la spettroscopia light beating (v. Cummins e Pike, 1973) è possibile misurare piccole velocità di particelle sospese in un liquido oppure la distribuzione delle velocità in un liquido o in altri materiali. Questo permette lo studio della dinamica di una transizione di fase e di altre instabilità, come l'instabilità di Taylor e le transizioni in cristalli nematici.
Con la spettroscopia laser a infrarosso è stato possibile scoprire venti con velocità di circa 5 m/s sul pianeta Venere. E possibile anche misurare emissioni non termiche dai pianeti (Marte e Venere) e la distribuzione dei vari gas nell'atmosfera terrestre.
4. Applicazioni della luce laser in altre discipline
Grazie alla grande densità di potenza, il laser può essere usato come strumento per effettuare saldature. È possibile saldare una lamina di acciaio di 5 cm di spessore con un laser di potenza pari a 100 kW. Per questo tipo di lavoro vengono usati soprattutto laser a gas dinamico.
Sempre in questo campo il laser può essere sfruttato per tagliare, per trapanare, per indurire una superficie mediante calore, per creare leghe sulle superfici, o anche per ottenere lo shock hardening.
Il laser glazing consiste nell'esporre brevemente un materiale, la cui superficie si vuole vetrificare, a un raggio laser con una densità di potenza compresa fra 104 e 107 W/cm2.
Sono previste molte applicazioni del laser in chimica, applicazioni basate sull'azione selettiva della luce laser su atomi e molecole. Tipici processi saranno la sintesi fotochimica e la dissociazione fotochimica.
È stato suggerito di utilizzare il laser nella propulsione di veicoli spaziali. Il propellente, liquido o solido, contenuto nella parte posteriore di un veicolo spaziale è colpito da luce laser proveniente da una sorgente remota. Il propellente passa quindi allo stato gassoso ed è poi portato a temperature molto alte (20.000 °K) da successivi impulsi del laser. L'espansione del gas spingerà quindi il veicolo spaziale.
Vi sono infine numerose applicazioni del laser in medicina, per esempio nel distacco della retina, nel trattamento di tumori, per esempio del tratto gastrointestinale (fotocoagulazione). Inoltre con un laser ad argon si possono trattare emangiomi, teleangectasie, radiodermatiti ed eseguire tatuaggi. È possibile infine utilizzare il laser in interventi chirurgici, anche sul cuore.
bibliografia
Abella, I. D., Kurnit, N. A., Hartmann, S. R., Photon echoes, in ‟Physical review", 1966, CXLI, pp. 391-406.
Allen, L., Eberly, J. H., Optical resonance and two-level atoms, New York 1975.
Arecchi, F. T., Degiorgio, V., Measurement of the statistical properties of optical fields, in Laser handbook (a cura di F. T. Arecchi e Q. E. Schulz-Dubois), Amsterdam 1972, pp. 191-264.
Arecchi, F. T., Giglio, M., Sona, A., Dynamics of the laser radiation at threshold, in ‟Physics letters", 1967, XXV A, pp. 341-342.
Basov, N. G., Prokhorov, A. M., Possible methods of obtaining active molecules for a molecular oscillator, in ‟Journal of experimental and theoretical physics", 1954, XXVII, p. 282; 1955, XXVIII, pp. 249-250.
Bloembergen, N., Nonlinear optics, New York 1965.
Bonifacio, R., Schwendimann, P., Haake, F., Quantum statistical theory of superradiance, in ‟Physical review", 1971, AIV(1), pp. 302-313; 1971, AIV(4), pp. 854-864.
Carmichael, H. J., Walls, D. F., A quantum-mechanical masterequation treatment of the dynamical Stark effect, in ‟Journal of physics", 1976, BIX(9), pp. 1199-1219.
Cummins, H. Z., Pike, E. R., Photon correlation and light beating spectroscopy, London 1973.
Degiorgio, V., Scully, M. O., Analogy between the laser threshold and a second order phase transition, in ‟Physical review", 1970, AII(2), pp. 1170-1177.
Dike, R. H., Coherence in spontaneous radiation processes, in ‟Physical review", 1954, XCIII, 1, pp. 99-110.
Einstein, A., Zur Quantentheorie der Strahlung, in ‟Physikalische Zeitschrift", 1917, XLIII, pp. 121-128.
Fabrikant, V. A.,??? in ‟Trudȳ Vsesoyuznogo élektrotekhnicheskogo instituta", 1940, XLI, p. 254.
Feynmann, R. P., Vernon, F. L., Hellwarth, R. W., Geometrical representation of the Schrödinger equation for solving maser problems, in ‟Journal of applied physics", 1957, XXVIII, pp. 49-52.
Glauber, R., Coherent and incoherent states of the radiation field, in ‟Physical review", 1963, CXXXI, pp. 2766-2788.
Gordon, J. P., Zeiger, H. J., Townes, C. H., Molecular microwave oscillator and new hyperfine structure in the microwave spectrum of NH2, in ‟Physical review", 1954, XCV, pp. 282-284.
Graham, R., Haken, H., Quantum theory of light propagation in a fluctuating laser-active medium, in ‟Zeitschrift für Physik", 1968, CCXIII, pp. 420-450.
Haken, H., Conference on optical pumping, Heidelberg 1962.
Haken, H., A nonlinear theory of laser noise and coherence, in ‟Zeitschrift für Physik", 1964, CLXXXI, pp. 96-124.
Haken, H., Laserlicht - ein neues Beispiel für eine Phasenumwandlung, in Festkörperprobleme (a cura di O. E. Madelung), vol. X, Braunschweig 1970, pp. 351-365.
Haken, H., Synergetics, an introduction. Nonequilibrium phasetransitions and selforganization in physics, chemistry and biology, Berlin-Heidelberg-New York 1977.
Haken, H., Sauermann, H., Nonlinear interaction of laser modes, in ‟Zeitschrift für Physik", 1963, CLXXIII, pp. 261-275.
Haken, H., Sauermann, H., Frequency shifts of laser modes in solid state and gaseous systems, in ‟Zeitschrift für Physik", 1963, CLXXVI, pp. 47-62.
Hellwarth, R. W., Control of fluorescent pulsations, in Advances in quantum electronics (a cura di J. Singer), New York 1961, pp. 334-341.
Hempstead, P. P., Lax, M., Classical noise. VI. Noise in selfsustained oscillators near threshold, in ‟Physical review", 1967, CLXI, 2, pp. 350-336.
Kaiser, W., Garett, G. C. B., Two-photon excitation in CaF2, Eu2+, in ‟Physical review letters", 1961, VII, pp. 229-231.
Kastler, A., Some suggestions concerning the optical production and optical detection of a population inequality among the spatial quantum levels of atoms, in ‟Journal de physique et le radium", 1950, XI, p. 225.
Lamb, W. E., Theory of an optical maser, in ‟Physical review", 1964, CXXXIV, pp. A1429-A1450.
Louisell, W. H., Quantum statistical properties of radiation, New York 1973.
MacCall, S. L., Instabilities in continuous-wave light propagation in absorbing media, in ‟Physical review", 1974, AIX(9), AIX(9), pp. 1515-1523.
MacCall, S. L., Hahn, E. L., Self-induced transparency, in ‟Physical review", 1969, pp. 457-485.
Maiman, T. H., Stimulated optical radiation in ruby, in ‟Nature", 1960, CLXXXVII, pp. 493-494.
Mandel, L., Wolf, E. (a cura di), Selected papers on coherence and fluctuations of light, voll. I e II, New York 1970.
Pike, E. R., Photon statistics, in Quantum optics (a cura di S. M. Kay e A. Maitland), London 1970, pp. 127-176.
Risken, H., Distribution and correlation functions for a laser amplitude, in ‟Zeitschrift für Physik", 1965, CLXXXVI, pp. 85-98.
Risken, H., Vollmer, H. D., The transient solution of the laser Fokker-Planck equation, in ‟Zeitschrift für Physik", 1967, CCIV, pp. 240-253.
Sargent III, M., Scully, M. O., Lamb, W. E. Jr., Laser physics, Reading, Mass., 1974.
Schawlow, A. L., Townes, C. H., Infrared and optical masers, in ‟Physical review", 1958, CXII, pp. 1940-1949.
Statz, H., Mars, G. A. de, Transients and oscillation pulses in masers, in Quantum electronics (a cura di C. H. Townes), New York 1960, pp. 530-537.
Szöke, A., Daneu, V., Goldhar, J., Kurnit, N. A., Bistable optical element and its applications, in ‟Applied physics lettes", 1969, XVI, pp. 376-379.
Weber, J., Amplification of microwave radiation by substances not in thermal equilibrium, in ‟IRE transactions ED-3", 1953, pp. 1-4.