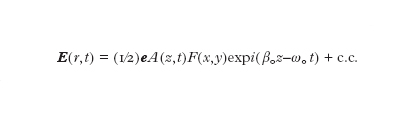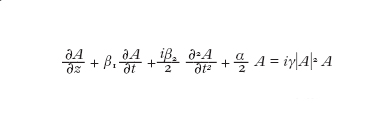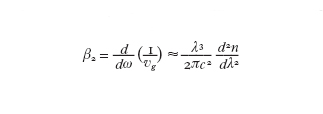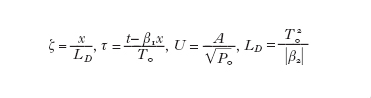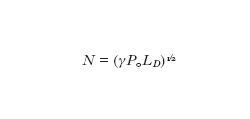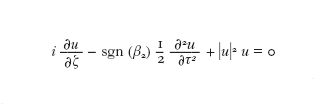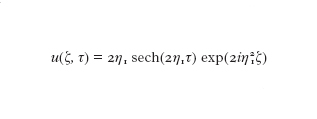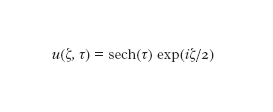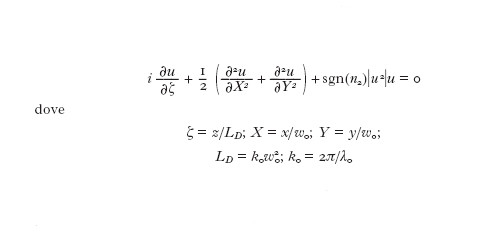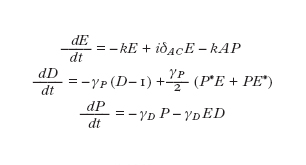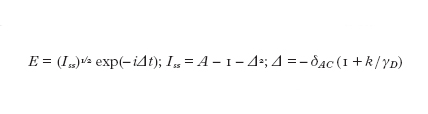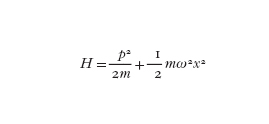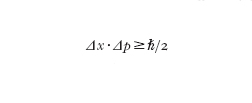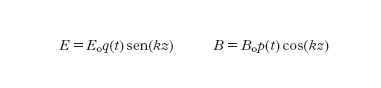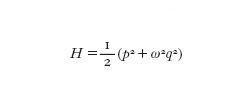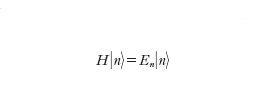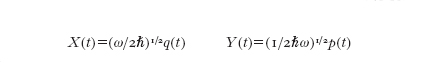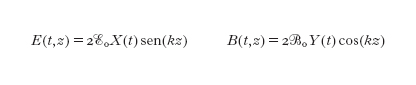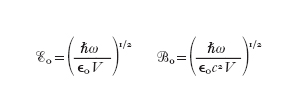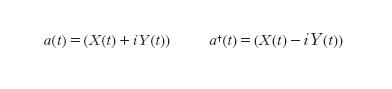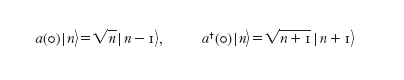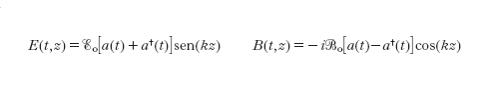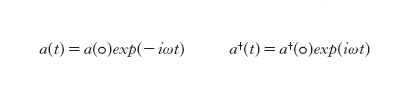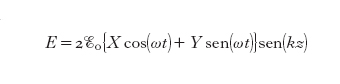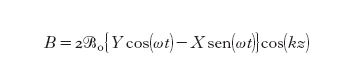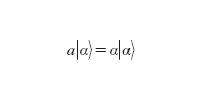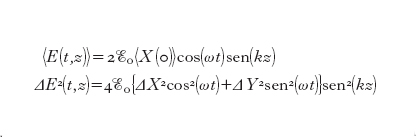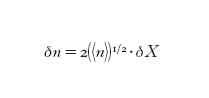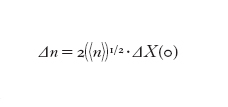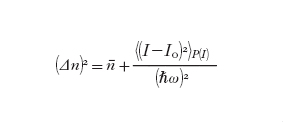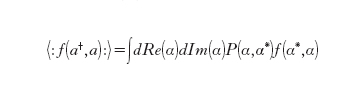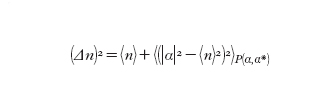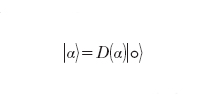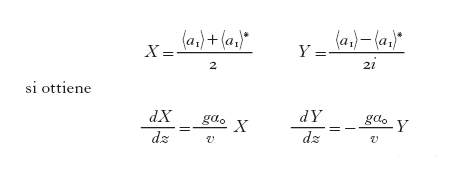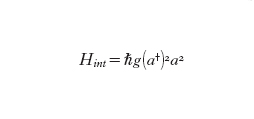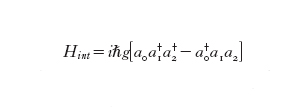OTTICA

Ottica

(XXV, p. 776; App. II, ii, p. 472; III, ii, p. 338; V, iii, p. 803; v. ottica non lineare, App. IV, ii, p. 701)

Ottica non lineare

di Mario Bertolotti

Negli ultimi anni l'o. ha subito un notevole sviluppo; la possibilità di controllare la luce con la luce, ovvero i fotoni con i fotoni, ha portato all'introduzione di una nuova disciplina, la fotonica (v. in questa Appendice), considerabile, in un certo senso, parallela all'elettronica, in quanto tende a realizzare dispositivi analoghi a quelli elettronici ma utilizzanti fotoni invece di elettroni. Pertanto, mentre la fotonica studia le applicazioni ai dispositivi, l'elettronica quantistica e l'o. lineare studiano i fenomeni di base. Il controllo di fotoni da parte di altri fotoni può ottenersi con le tecniche dell'o. non lineare, trattata nella voce ottica non lineare dell'App. IV e ripresa nella voce ottica dell'App. V.

Le non linearità ottiche possono essere tutto ottiche o ibride. Le non linearità tutto ottiche, essenzialmente, sono connesse a moti di elettroni di valenza e sono in genere più deboli di quelle ibride, dove il moto degli ioni (vibrazionale, rotazionale, traslazionale o una combinazione di questi) può generare non linearità molto alte. L'instaurarsi delle prime è molto più rapido di quello delle seconde. Le caratteristiche delle non linearità, per quanto concerne l'ampiezza e la sua variazione temporale, sono essenziali in ogni valutazione dei materiali da usare. Tali caratteristiche dipendono fortemente da quanto la frequenza di operazione è vicina alla risonanza del materiale, poiché il verificarsi di questa condizione introduce un aumento della non linearità, perdite per assorbimento e, inoltre, limita la velocità a causa dei processi di rilassamento. Le perdite possono avvenire per assorbimento lineare (fotone singolo) o non lineare (più fotoni), e possono essere connesse solo alla parte immaginaria delle suscettibilità di ordine dispari (v. oltre); infatti non ci sono perdite per assorbimento connesse a processi non lineari di ordine pari. Inoltre, è anche necessario tener conto della possibilità che il materiale si danneggi sotto l'effetto della radiazione. Il danno può risultare da rottura dei legami di origine fotochimica o termica, breakdown ottico e molti altri processi direttamente connessi con l'interazione della radiazione con la materia. I materiali non lineari, sulla base delle forze che legano le cariche e le unità polarizzabili in essi, possono essere divisi in: cristalli ionici, essenzialmente solidi basati su poliedri di ossigeno; cristalli covalenti, essenzialmente semiconduttori; cristalli molecolari, in particolare cristalli organici e polimerici, cristalli liquidi; solidi disordinati e amorfi, in particolare vetri e polimeri; solidi compositi e artificialmente inomogenei.

I materiali organici si sono rivelati durante gli anni Ottanta un'importante classe di materiali ottici non lineari con caratteristiche uniche.

Essi presentano un insieme di unità molecolari interagenti debolmente tra loro mediante forze di van der Waals. In questo caso, la risposta non lineare ottica può essere descritta principalmente come connessa a una deformazione delle nubi elettroniche entro ogni molecola per la presenza dell'intenso campo elettrico dell'impulso ottico applicato. I materiali organici mostrano quindi una non linearità ottica di tipo molecolare, a differenza di quanto accade nei semiconduttori inorganici o nei cristalli ionici dove, non essendo presente alcuna unità molecolare singola nel volume, la non linearità è un effetto di volume.

Negli ultimi anni, un'intensa ricerca è stata fatta sui cristalli organici e sulla possibilità di ottenere strutture ordinate organiche. Si è sintetizzata e studiata una serie di nuovi materiali caratterizzati da grande non linearità e alte soglie di danno. Inoltre, l'uso di materiali organici ha ricevuto fortissimo impulso nei confronti sia dei materiali amorfi per processi del terzo ordine, sia dei materiali ordinati usando varie tecniche di poling per processi quadratici.

In molti polimeri organici di ottima qualità ottica si può introdurre e disperdere in modo uniforme una gran quantità di molecole organiche con elevata polarizzabilità dovuta a trasferimento di carica. Se si vogliono ottenere materiali in cui le molecole sono orientate in modo casuale, la soluzione del polimero e delle molecole ospiti viene depositata mediante spin-coating o altre tecniche. Se si vuole un materiale con proprietà non lineari del secondo ordine è necessario invece orientare le molecole, per es. mediante la tecnica del poling, cioè applicando un forte campo elettrostatico (electrode poling) o una scarica a corona (corona poling) a una temperatura vicina alla temperatura T_g di transizione a una fase plastica, dove possono manifestarsi sia la flessibilità collettiva delle molecole sia il moto molecolare a grandi distanze.

fig. 1A

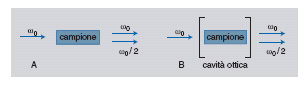
Scegliendo opportunamente il polimero, la temperatura di transizione può essere maggiore della temperatura estrema di operazione del materiale nelle applicazioni pratiche, ottenendo così eccellenti materiali. Per quanto riguarda le molecole introdotte è possibile avere: a) sistemi in cui le molecole ospiti non sono attaccate alla catena polimerica e possono ruotare liberamente a temperature prossime a T_g; b) polimeri a catena laterale (side-chain) in cui un'estremità della molecola non lineare reagisce chimicamente e si attacca al polimero ma ha l'altro estremo libero (fig. 1A); c) polimeri cross-linked (a legami incrociati, cioè a struttura reticolata) in cui entrambe le estremità della molecola ospite reagiscono chimicamente e si attaccano alla catena polimerica mediante legami covalenti (fig. 1B); d) sistemi a catena principale in cui le molecole sono inserite proprio nella catena polimerica.

I polimeri sottoposti a poling offrono vantaggi notevoli rispetto ai materiali cristallini, poiché presentano migliori caratteristiche di non linearità, qualità ottica, lavorazione, interfacciamento, accordabilità di fase ecc. Il problema della stabilità all'invecchiamento, tipico dei polimeri e connesso a una diminuzione del grado di allineamento delle molecole, si sta gradualmente superando. I migliori risultati si sono ottenuti con polimeri cross-linked, anche se non sono da sottovalutare quelli del tipo side-chain.

Tra le più alte non linearità del terzo ordine si registrano quelle presentate da una vasta classe di polimeri coniugati, tra i quali i polidiacetileni. Con tali materiali si formano inizialmente dei cristalli di buona qualità con monomeri di diacetilene R₁-C=C-C-R₂, dove R₁ ed R₂ sono radicali scelti in modo opportuno; successivamente li si polimerizza mediante trattamento termico, azioni meccaniche o radiazione UV, ottenendo così cristalli polimerici coniugati che tuttavia presentano sempre difetti di vario tipo.

Un altro metodo per aumentare la non linearità, specialmente usato per i materiali ottici del terzo ordine, consiste nel confinare artificialmente gli elettroni in regioni molto più piccole della loro regione di delocalizzazione abituale nei cristalli massivi. Al processo è associata la comparsa di risonanze che aumentano notevolmente la risposta non lineare. È possibile avere due tipi di confinamento: nei nanocristalli di semiconduttori si ha quello quantico, mentre nei nanocristalli metallici si ha quello dielettrico. Sfruttando tale processo si sono realizzati e studiati vetri con nanocristalli dispersi, sia di semiconduttori sia di metalli, che hanno fornito risposte non lineari del terzo ordine notevolmente alte.

Processi del secondo ordine

Processi parametrici e produzione di seconda armonica. - Tra i fenomeni del secondo ordine, i processi parametrici e la produzione di seconda armonica sono stati ovviamente i più studiati. Il processo di conversione di o. parametrica, sebbene sia concettualmente semplice ed elegante, ha comportato all'inizio una serie di problemi dovuti alla bassa efficienza e alla cattiva qualità dei fasci di pompa in uso all'epoca. Più recentemente, tuttavia, questi problemi sono stati superati, in primo luogo grazie all'impiego di nuovi cristalli non lineari con alte soglie di danneggiamento, come il KTP (fosfato di potassio e titanile), BBO (borato di bario), LiBO (triborato di litio), in secondo luogo grazie allo sviluppo di una nuova generazione di laser efficienti, generanti impulsi brevi nel campo dei picosecondi e dei femtosecondi con modi singoli trasversi e alto grado di stabilità da impulso a impulso. In particolare, l'uso di impulsi ultracorti ha consentito di avere guadagni parametrici nettamente più alti, poiché il guadagno è determinato dalla potenza istantanea e inoltre l'intensità di soglia per il danno, per impulsi brevi, aumenta al diminuire della durata degli impulsi.

Tuttavia la conversione parametrica con sorgenti di pompa generanti impulsi ai picosecondi e ai femtosecondi ha posto un ulteriore problema: la breve durata dell'impulso preclude l'uso della cavità standard per l'oscillatore parametrico (OPO, Optical Parametric Oscillator) in cui i campi oscillanti si costruiscono durante la durata dell'impulso di pompa. Una tale cavità dovrebbe essere lunga solo pochi millimetri per un sistema operante al picosecondo e ancor meno per impulsi al femtosecondo, divenendo così impraticabile. Per ovviare a questa limitazione si sono usati principalmente due differenti metodi. Il primo impiega il pompaggio sincrono di un OPO, introdotto da K. Burneika e collab. nel 1972, ed esteso poi al pompaggio con treni di impulsi da laser in regime continuo a modi bloccati (mode-locked), oppure il pompaggio con diodi laser (o tutto solido). L'altro metodo consiste nell'utilizzo di un generatore parametrico a onda viaggiante (metodo impiegato da A. Piskarskas e collab., D.R. Walker e collab., H.J. Krause e collab., W. Daum negli anni 1992-96).

Per la generazione di seconda armonica ha acquistato notevole importanza l'uso di guide d'onda. Vi sono essenzialmente due vantaggi che rendono tali guide d'onda attraenti per l'o. integrata del secondo ordine a bassa potenza: il primo è dovuto al fatto che in una guida d'onda la luce può essere confinata in un'area molto piccola per distanze sufficientemente lunghe, cosicché anche sorgenti di pompa di potenze moderate o basse possono produrre interazioni efficienti; il secondo vantaggio deriva dal fatto che la condizione di phase-matching (adattamento di fase) o di quasi phase-matching (QPM, v. oltre) viene ottenuta sfruttando gli indici effettivi dei modi guidati invece che gli indici del materiale. Tuttavia è necessario precisare che tali vantaggi sono strettamente limitati alla possibilità di massimizzare la sovrapposizione fra i modi interagenti.

Nell'ambito delle tecniche con guide d'onda sono state studiate diverse realizzazioni usando differenti materiali (principalmente niobato di litio, semiconduttori e polimeri organici). In particolare, nelle guide a niobato di litio, per un'accordabilità fine si sfrutta la birifrangenza combinata a un aggiustamento in temperatura.

Un metodo alternativo per ottenere la condizione di phase-matching è il cosiddetto schema Čerenkov, in cui si crea un'onda di polarizzazione a frequenza 2f che viaggia con una velocità di fase maggiore di quella della rispettiva onda elettromagnetica a frequenza 2f, sicché questa polarizzazione è sorgente di un modo di radiazione caratterizzato da un angolo di propagazione che soddisfa la condizione di phase-matching. Tale tecnica è stata per es. usata per la generazione di luce blu; in particolare, T. Taniuchi e K. Yamamoto (1996) hanno ottenuto 1,6 mW nel blu usando 100 mW di luce a frequenza fondamentale lanciata nella guida.

2

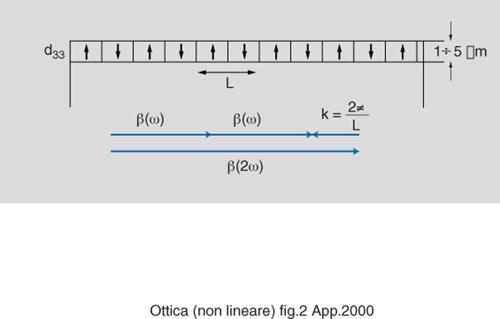
Un'altra tecnica per ottenere un'efficiente produzione di seconda armonica in guida è il cosiddetto quasi phase-matching (fig. 2), che fu già proposto da N. Bloenbergen e collab. nel 1962. Nello schema proposto si utilizzava un mezzo in cui, dopo ogni lunghezza di coerenza, il segno della non linearità veniva invertito in modo da riportare a zero l'errore di fase accumulato su una tale lunghezza, permettendo così all'emissione di armonica da ogni successiva lunghezza di coerenza di sommarsi in fase. In altre parole, la tecnica QPM si basa sulla modulazione periodica della suscettibilità non lineare e/o dell'indice di rifrazione; la modulazione introduce un vettore d'onda addizionale da un reticolo che può compensare il non perfetto adattamento fra il vettore d'onda delle onde fondamentali e quello di seconda armonica.

Nei materiali anisotropi, per un'onda straordinaria non propagantesi lungo una direzione principale la direzione di propagazione dell'onda e quella di propagazione dell'energia sono in generale differenti. La propagazione collineare dei vettori d'onda non corrisponde quindi, in generale, a una propagazione collineare dell'energia (walk-off). Con la tecnica del QPM si può ottenere phase matching non critico a un'opportuna temperatura senza introdurre walk-off spaziale. In tal modo si possono utilizzare materiali con le più alte non linearità per i quali spesso non è possibile realizzare l'adattamento in fase selezionando l'angolo o la temperatura. La tecnica del QPM fu dimostrata sperimentalmente da D.E. Thompson e collab. nel 1976 usando una serie di strati di GaAs orientati differentemente per la duplicazione di frequenza di radiazione a 10,6 μm. Alla fine degli anni Ottanta una realizzazione pratica ed elegante è stata ottenuta in cristalli ferroelettrici sottoposti a poling periodico, come il niobato di litio, il tantalato di litio e il KTP, per i quali si sono ottenuti risultati sperimentali sia in guide sia in materiali massivi. Più recentemente, è stata dimostrata da M.W. Street e collab. (1997) la possibilità di usare strutture periodiche quali le eterostrutture a buca quantica multipla (multiquantum wells) in AlGaAs.

Relativamente alle guide ottiche si è infine studiata l'amplificazione parametrica e l'oscillazione, e sono state investigate sperimentalmente (per es. da A. Fiore e collab., 1997) sorgenti accordabili nel medio infrarosso attraverso generazione di frequenze differenza in guide di GaAs.

Generazione di seconda armonica in materiali con inversione di simmetria. - Un nuovo e interessante fenomeno è costituito dalla produzione di seconda armonica in materiali amorfi come le fibre ottiche.

Da un punto di vista teorico, la produzione di seconda armonica in un materiale in cui è presente un'inversione di simmetria dovrebbe essere trascurabile. Per questo motivo, quando U. Osterberg e W. Margukis (1986) e R.H. Stolen e H.W.K. Tom (1987) riferirono di aver raggiunto un'efficiente produzione di seconda armonica in fibre di breve lunghezza, la notizia fu accolta con grande sorpresa. Si sono ottenute, per es., efficienze di conversione del 5% in soli 50 cm di fibra con potenze di picco d'entrata di 20 kW a 1,064 μm. La spiegazione teorica di tale processo è stata data da E.M. Dianov e collab. (1989) sulla base dell'effetto fotogalvanico coerente.

Un campo elettrostatico (10⁴÷10⁵ V/cm) oscillante spazialmente si presenta nel vetro come risultato della separazione di carica indotta da una fotocorrente coerente oscillante con un periodo determinato dal disaccordo della velocità di fase fra pompa e seconda armonica. Questo campo elettrico produce un reticolo di QPM proporzionale a χ⁽³⁾ che permette di produrre seconda armonica in modo efficiente. Dopo i primi risultati sperimentali si sono usate anche numerose tecniche di poling del vetro che hanno permesso di produrre non linearità del second'ordine prossime a 1 pm/V, molto vicine alle non linearità standard di cristalli non centrosimmetrici come KTP, KDP (fosfato biacido di potassio) ecc., dando la possibilità concreta di costruire convertitori di frequenza efficienti a basso costo, modulatori elettro-ottici e otturatori monolitici integrati in fibre ottiche o guide planari di vetro (1994).

Effetto cascata (cascading). - L'effetto, previsto da N. Blombergen e studiato fin dagli anni Sessanta da L.A. Ostrovskij (1967) e altri, è stato riconsiderato negli anni Ottanta, principalmente in connessione al problema di cercare un mezzo con risposta ultraveloce, privo di perdite ed efficiente, per elaborare i segnali ottici, e ha finalmente ricevuto conferma sperimentale da J.R. De Salvo e altri nel 1992.

Esso si basa sul fatto che in assenza di perfetto phase-matching, in un cristallo non centrosimmetrico dopo una lunghezza di coerenza dell'interazione, la potenza è di nuovo trasferita dal campo a frequenza doppia al campo a frequenza fondamentale. Ma tale campo riconvertito per un certo tempo si è propagato con la velocità della seconda armonica e non è quindi più in fase con il campo fondamentale che si è propagato indisturbato.Il risultato è che il campo totale a frequenza fondamentale viene sfasato di un termine addizionale che dipende dall'intensità del campo riconvertito, e quindi viene a dipendere in modo complicato dall'intensità totale del campo a frequenza fondamentale. In un certo senso tutto va come se l'indice di rifrazione del materiale fosse variato in funzione dell'intensità dell'onda, il che è un effetto del terzo ordine.

A tale effetto non sono associate le perdite tipiche dei materiali del terz'ordine ed esso risulta caratterizzato da una risposta più veloce rispetto a questi, circostanza che giustifica il grande interesse attualmente riposto in questo effetto per costruire dispositivi tutto ottici.

Processi del terzo ordine

Solitoni. - Passando a considerare l'uso di non linearità del terzo ordine c'è stato un grande sviluppo di ricerche, seguito da numerose applicazioni, sugli effetti in cui l'indice di rifrazione del mezzo viene a dipendere dall'intensità del fascio (effetto Kerr ottico) e che si presentano nei cosiddetti fenomeni di autofocalizzazione (self-focusing) o autodefocalizzazione (self-defocusing). Sfruttando tali effetti sono stati progettati e realizzati numerosi dispositivi quali interruttori ottici o deviatori. Gli effetti del terzo ordine sono rilevanti nel caso risonante in cui si accompagnano a un notevole assorbimento e non risultano caratterizzati da tempi di risposta rapidi: questo è uno dei motivi per cui si è data molta enfasi negli ultimi anni al cascading, che si produce invece negli effetti del secondo ordine.

Una delle applicazioni più interessanti degli effetti del terzo ordine si ha nei solitoni. Il termine fu coniato nel 1965 per descrivere una proprietà rimarchevole della propagazione ondosa in mezzi non lineari che si manifesta attraverso proprietà dell'inviluppo dell'onda simili a quelle di una particella. Nel caso dei solitoni temporali, sotto particolari condizioni, un bilanciamento fra gli effetti dispersivi e quelli non lineari può portare a inviluppi dell'impulso che conservano la loro forma temporale non solo durante la propagazione ma anche durante collisioni mutue. Il termine onde solitarie è invece talora usato per descrivere la situazione in cui l'inviluppo preserva la sua forma durante la propagazione, ma non a seguito di collisioni.

Più precisamente, l'allargamento temporale di un impulso in un materiale dispersivo a causa della dispersione cromatica, può essere compensato dalla contrazione associata con l'automodulazione di fase, cosicché un impulso stretto può propagarsi senza allargarsi nel tempo. A. Hasegawa e F.D. Tappert (1973) suggerirono che i solitoni temporali potessero essere ottenuti in regime di dispersione anomala nelle fibre ottiche e applicati alle comunicazioni ad altissima velocità. Il campo elettrico di un'onda polarizzata propagantesi in una fibra può scriversi:

formula [

1]

dove e è il versore che descrive la direzione della polarizzazione, β₀ è la costante di propagazione, ω₀ è la pulsazione a cui lo spettro dell'impulso è centrato, c.c. indica il complesso coniugato dell'espressione che lo precede e F(x,y) rappresenta la distribuzione modale che si suppone non venga influenzata dalla non linearità che è assunta essere piccola. Tenendo conto degli effetti di dispersione della fibra e dell'andamento non lineare dell'indice di rifrazione si ottiene alla fine un'equazione per l'ampiezza dell'inviluppo A(z,t):

formula

[2]

dove γ è il parametro non lineare, pari a γ = n₂ω₀/(cA_eff), con A_eff area effettiva del nucleo della fibra, n₂ coefficiente non lineare dell'indice di rifrazione n=n₀+n₂I, con I intensità dell'onda, α è il coefficiente di attenuazione della fibra, β₁ e β₂ hanno origine nella dipendenza dalla frequenza della costante di propagazione. In particolare, β₁=1/v_g con v_g, velocità di gruppo, mentre

formula [

3]

prende il nome di parametro della dispersione della velocità di gruppo. La dispersione della velocità di gruppo è detta normale o anomala a seconda che β₂ sia positivo o negativo. Introducendo le variabili normalizzate

formula [

4]

dove T₀ è una misura della durata dell'impulso e P₀ è la potenza di picco dell'impulso, trascurando le perdite α e definendo u=NU, con

formula [

5]

si ottiene:

formula [

6]

La soluzione della [6] dipende dal segno di β₂: le soluzioni a forma di impulso si ottengono solo con β₂ positivo (dispersione anomala) e sono dette solitoni bright (solitoni luminosi). Nel caso di dispersione normale (β₂〈0) le soluzioni di onda solitaria appaiono come una mancanza di segnale su uno sfondo costante e sono dette solitoni dark (solitoni scuri). A seconda dei valori della grandezza N definita nella [5], si hanno vari tipi di soluzioni della [6]. La soluzione per N=1 prende il nome di solitone fondamentale. L'ampiezza del solitone fondamentale è descritta in termini di un singolo parametro η₁ dall'equazione:

formula [

7]

Il valore di η₁ è determinato dal campo incidente u(0,τ). La forma canonica del solitone fondamentale è ottenuta prendendo u(0,0)=1, cosicché 2η₁=1 e la [7] si scrive:

formula [

8]

La soluzione [8] è centrata a τ=0 e decade a zero da entrambi i lati. La proprietà più importante del solitone fondamentale è che ∣u(π, τ)∣² è indipendente da π: ciò significa che un impulso a secante iperbolica di larghezza T₀ e potenza di picco P₀, tali che N=1, si propaga senza cambiare forma per distanze arbitrariamente grandi. La potenza di picco richiesta per lanciare un solitone fondamentale è P₀ = ∣β₂∣ / (γT₀²).

fig. 3

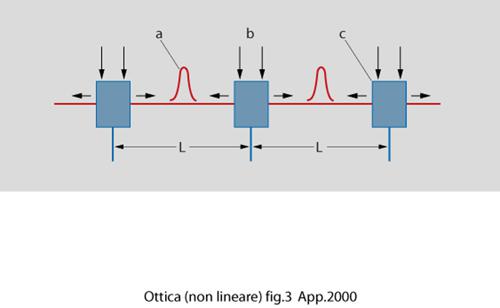
Se la forma dell'impulso o la potenza d'ingresso deviano dalle condizioni ideali, l'impulso cerca di formare un solitone aggiustando la sua forma e larghezza. In un certo senso, i solitoni in fibra sono modi naturali della propagazione in presenza di dispersione e non linearità e sono quindi un'entità stabile e robusta. La natura robusta dei solitoni in fibra li rende candidati ideali per applicazioni in sistemi di comunicazioni ottiche su grandi distanze ad alta velocità. Le caratteristiche di tali sistemi di comunicazione sono spesso limitate dalla dispersione delle fibre, che allarga gli impulsi. L'uso dei solitoni temporali risolve questo problema perché gli effetti della dispersione della velocità di gruppo sono compensati dalla non linearità della fibra: la limitazione fondamentale di un tale approccio è dovuta alle perdite della fibra. La larghezza del solitone, infatti, inizia ad aumentare a causa della diminuzione della potenza di picco durante la propagazione. Per compensare questo effetto è necessario amplificare periodicamente i solitoni. La fig. 3 illustra lo schema di base. I solitoni sono lanciati nel collegamento a fibra che consiste di molti segmenti di lunghezza L. Alla fine di ogni segmento, dei laser di pompa iniettano della luce in potenza continua con una frequenza spostata verso le frequenze superiori rispetto alla frequenza della portante del solitone, che è di circa 13 THz. Sfruttando la non linearità della fibra si ha amplificazione per effetto Raman stimolato adiabaticamente lungo tutta la fibra. Per una velocità di trasmissione di 5 Gbit/s si sono trasmessi impulsi fino a 6000 km.

I due parametri di progetto sono il bit rate B e la lunghezza del segmento L. Generalmente L varia come B⁻². Il bit rate B è determinato dalla necessità di impedire interazione fra solitoni vicini; se q è la separazione relativa fra solitoni di durata T, si ha B=(2qT)⁻¹. Tipicamente q=8¸10 (nelle unità normalizzate che sono state definite nelle [4]) e L= 30¸40 km; per B=5 Gbit/s, con q=10, la larghezza del solitone risulta T=10 ps. La potenza di picco richiesta per β₂=-2 ps²/km è 10 mW.

È possibile avere anche solitoni spaziali, cioè propagazione di fasci in continua in mezzi non lineari tali che la larghezza trasversale del fascio non cambi durante la propagazione. Nel caso di mezzi Kerr, i solitoni spaziali possono prodursi da un bilancio fra la diffrazione e l'autofocalizzazione. In questo caso il ruolo della dispersione è rimpiazzato dalla diffrazione: la propagazione dell'onda è governata dallo stesso tipo di equazione di Schrödinger non lineare usata per la descrizione dei solitoni temporali, con la differenza che si devono considerare due dimensioni trasverse.

La [6] è sostituita dalla equazione:

formula [

9]

w₀ è la larghezza dell'impulso all'entrata.

Per n₂〈0 il fenomeno dell'autofocalizzazione allarga il fascio insieme alla diffrazione e il solitone spaziale non può esistere, mentre per n₂>0 l'autofocalizzazione controbilancia la diffrazione e il profilo può rimanere invariato. I solitoni spaziali furono trovati come soluzione dell'equazione [9] nel 1964. La soluzione di autointrappolamento tuttavia è instabile: un piccolo aumento della potenza del fascio porta a una catastrofica autofocalizzazione, e a filamentazione. Tale comportamento dipende dal fatto che si ha a che fare con due dimensioni: se si considera una situazione in cui il fascio è già in una dimensione, come è per es. in una guida d'onda, la [9] diventa identica alla [6] ed è possibile avere soluzioni di solitoni stabili.

Un solitone spaziale può essere definito come un fascio che si propaga senza diffrazione. Per ottenere questo risultato è necessario compensare l'allargamento spaziale del fascio, dovuto alla diffrazione, con una uguale quantità di autofocalizzazione che mantenga costante la sezione trasversale del fascio durante la propagazione.

fig. 4A

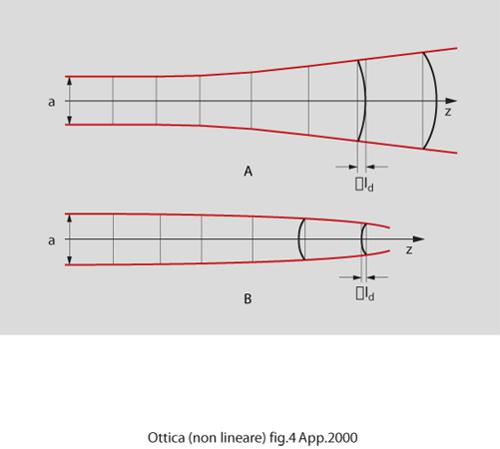
Senza risolvere la [9], un calcolo molto semplice mostra che questo è possibile. A basse intensità l'effetto Kerr non lineare può essere trascurato. Il fascio si allarga per diffrazione (fig. 4A) inducendo una curvatura positiva del fronte d'onda. Per un'onda piana, inizialmente limitata, l'insellamento dopo propagazione per una distanza z è Δl_d = z[1 - cos(α/2)], dove l'angolo di divergenza è α = λ/(an₀), essendo a la larghezza iniziale del fascio. Invece, un intenso fascio a singolo modo con un profilo d'intensità a campana genera una distribuzione di indice di rifrazione che si comporta come una lente spessa a gradiente d'indice se il mezzo è self-focusing. Il fascio si focheggia, dando luogo a una curvatura negativa del fronte d'onda (fig. 4B). Assumendo che la diffrazione sia trascurata, si può scrivere Δl_NL= = -n₂∣E∣² z. Un bilanciamento fra l'effetto Kerr e l'effetto della diffrazione si ha se Δl_d = Δl_NL. La corrispondente densità di potenza è ∣E∣²=λ²/(8a²n₂ n²₀), che corrisponde a una potenza totale del fascio P_c = a² ∣E∣² = λ²/(8n₂ n²₀), che non dipende dai parametri geometrici del fascio e, quindi, ogni fluttuazione nella potenza P portata dal fascio fa sì che esso si focheggi (P>P_c ) o diverga (P〈P_c). La propagazione tridimensionale in mezzi Kerr non lineari è quindi instabile a meno che non si prenda qualche accorgimento particolare come l'uso di una tecnica interferenziale o di guide d'onda che già confinano il fascio in una direzione. In quest'ultimo caso, un fascio in una guida con larghezza a e spessore costante b è in equilibrio se P = ab∣E∣² = λ²b/8an₂ n²₀, che dipende dalla larghezza del fascio. Se la potenza è troppo bassa, l'allargamento dovuto alla diffrazione aumenta la larghezza del fascio finché non si ha Pa = λ²b/8n₂n²₀ e così l'equilibrio è raggiunto. Al contrario, se la potenza è troppo alta, la larghezza diminuisce finché a è tale che Pa = λ²b/8n₂n²₀ e di nuovo si ottiene l'equilibrio: un solitone di questo tipo, è detto solitone fondamentale.

Una proprietà molto interessante dei solitoni è la loro capacità di interagire se sono sufficientemente vicini.

fig. 5A

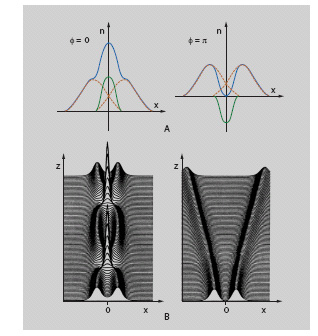
Se due solitoni fondamentali di ampiezza E₁ ed E₂ si propagano simultaneamente, la parte non lineare dell'indice di rifrazione può essere scritta come n_NL = n₂ [∣E₁∣² + ∣E₂∣² + 2Re(E₁E₂*)]. Il termine misto con E₁E₂* può essere positivo o negativo a seconda della fase relativa fra i due solitoni. La presenza di tale termine dà luogo alla possibilità di interazione. La fig. 5A mostra il profilo dell'indice di rifrazione indotto quando la fase relativa ϕ è pari a 0 o π. Se i campi ottici E₁ ed E₂ sono in fase, i lati dei solitoni vicini all'asse di simmetria vengono ritardati e i due solitoni convergono; al contrario, se i due solitoni sono in opposizione di fase, essi divergono. La fig. 5B mostra una simulazione numerica di questi effetti.

Esiste comunque una classe più generale di fasci che a causa della non linearità possono propagarsi senza diffrangersi. Tali fasci, che danno luogo a una vasta varietà di distribuzioni spaziali, sono genericamente indicati come fasci senza diffrazione (free diffraction beams). Essi esistono anche nel caso di propagazione lineare, ma le possibilità offerte dai fenomeni non lineari aumentano enormemente la varietà di situazioni che è possibile ottenere. Fasci senza diffrazione, e più in particolare solitoni spaziali, possono essere ottenuti anche sfruttando l'effetto di cascata in materiali del secondo ordine. In questo caso, la circostanza che si può avere l'interazione del secondo ordine solo in direzioni ben precise, a causa dei problemi di accordo di fase, consente di avere situazioni stabili anche a tre dimensioni nel volume del cristallo non lineare.

Sebbene lo studio delle onde solitarie nei mezzi quadratici sia iniziato negli anni Settanta, solo recentemente si è avuto un risveglio dell'attenzione, soprattutto in connessione alla possibilità di costruire dispositivi tutto ottici efficienti. Nel 1995 sono state osservate sperimentalmente onde spaziali solitarie in un mezzo quadratico (KTP) in geometria tridimensionale.

Si è anche studiata la possibilità di ottenere onde solitarie spaziali in materiali con QPM, in quanto queste potrebbero fornire la possibilità di costruire dispositivi altamente efficienti, essendo possibile la formazione di onde solitarie a livelli di potenza ridotti rispetto al livello di potenza generalmente necessario per la loro formazione nei materiali quadratici standard, i cui coefficienti più alti di non linearità del secondo ordine sono spesso non accordabili in fase mediante variazioni di angolo o temperatura. Il reticolo di QPM induce in un mezzo quadratico una non linearità addizionale formalmente analoga a una non linearità cubica. Si ha una competizione indotta fra effetti quadratici e cubici che potrebbe condurre a caratteristiche più efficienti di commutazione tutto ottica.

Coniugazione di fase. - La coniugazione di fase ottica è un'interazione non lineare che genera un fronte d'onda coniugato in fase. Un dispositivo che produce un tale fronte d'onda è detto specchio coniugato in fase.

fig. 6A

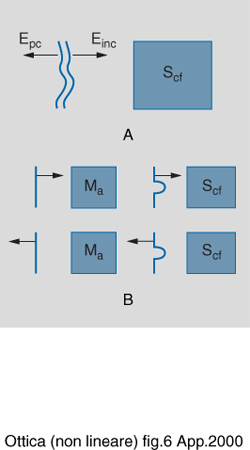
L'idea base della coniugazione di fase è illustrata nella fig. 6A. Il campo E_inc (γ, t) = Re[ε_inc exp(-iωt)], con ε_inc ampiezza complessa, incide sullo specchio coniugato in fase (S_cf) e un processo non lineare ottico genera l'onda E_pc (γ, t) = Re[r_c ε^*_inc exp(-iωt)], detta onda coniugata in fase. La costante r_c dell'espressione precedente, dove ε^*_inc è l'ampiezza complessa coniugata di ε_inc, è nota come riflessione d'ampiezza della coniugata in fase. Nella riflessione da un tale specchio, la porzione più avanzata del fronte d'onda incidente genera la parte più ritardata del fronte d'onda coniugato in fase. Questa proprietà è l'opposto di quanto avviene nella riflessione da uno specchio ordinario.

Una delle applicazioni principali della coniugazione di fase è la rimozione delle aberrazioni dai sistemi ottici.

La fig. 6B illustra schematicamente il processo di correzione delle aberrazioni. Un fronte d'onda incidente, presentato come un'onda piana, passa attraverso un mezzo aberrante (M_a) e ne fuoriesce distorto. Dopo riflessione da uno specchio coniugato in fase (S_cf), il senso delle distorsioni è invertito, e dopo aver attraversato nuovamente il mezzo aberrante la distorsione del fronte d'onda è rimossa. I principali mezzi per generare un fronte d'onda coniugato sono il degenerate four wave mixing (v. ottica a coniugazione di fase, App. V) e lo scattering stimolato.

fig. 7

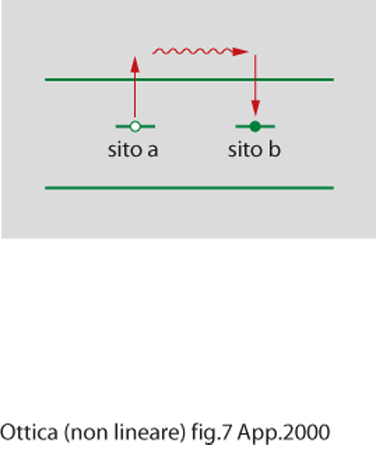
Effetto fotorifrattivo. - Si tratta di un processo ottico che può portare a una larga risposta non lineare e richiede solo milliwatt (o meno) di potenza laser. I tempi di risposta sono assai lenti, dell'ordine del decimo di secondo. L'effetto fotorifrattivo può essere descritto matematicamente da un insieme di equazioni introdotte da N. Kuchtarev nel 1979. Qui presenteremo solo un modello qualitativo che spiega la natura dell'effetto. Esso si presenta nei cristalli per i quali si ha l'effetto elettroottico lineare e che contengono portatori di carica (elettroni o lacune) la cui distribuzione spaziale può essere modificata dalla luce. La natura di questa ridistribuzione è illustrata nella fig. 7 per il caso in cui i portatori di carica siano elettroni. Qui un elettrone, che è legato inizialmente a un'impurità donatrice posta nel sito a è fotoeccitato nella banda di conduzione del materiale, dove può muoversi per diffusione termica o sotto l'azione di un campo elettrico statico. L'elettrone, successivamente, si ricombina con un donatore ionizzato presente nel sito b. Se l'intensità I(r) della luce nel cristallo non è uniforme, la densità di carica ϱ(r) dentro il materiale diventa non uniforme perché gli elettroni tenderanno a migrare dalle regioni ad alta a quelle a bassa intensità luminosa. Questa distribuzione di carica non uniforme produrrà un campo elettrico statico non uniforme E(r) che cambierà le proprietà ottiche del materiale per mezzo dell'effetto elettroottico lineare. Si ha così una variazione dell'indice di rifrazione.

Si supponga, per es., che due fasci di luce interferiscano nel cristallo per produrre una distribuzione d'intensità della forma I(x)=I₀ + I₁cos(qx). In molti casi, la distribuzione della densità di carica nel cristallo è allora della forma ϱ(x) = ϱ₁ cos(qx), dove l'ampiezza ϱ₁ della variazione della densità di carica dipende dalle proprietà del mezzo. La variazione del campo elettrostatico risulta allora della forma E(x) = E₀ + E₁ sen(qx) e si produce una variazione di indice di rifrazione Δn(x) = n₁ sen(qx). Si osservi che Δn(x) è spostato in fase rispetto alla distribuzione d'intensità I(x): questo spostamento in fase porta a un trasferimento di energia fra i due fasci interagenti in un cristallo fotorifrattivo. Questo trasferimento di energia è conosciuto come accoppiamento a due onde. Esso gioca un ruolo importante, per es., nella realizzazione di specchi a coniugazione di fase per mezzo dell'effetto fotorifrattivo.

Impulsi ultracorti. - Negli ultimi dieci anni sono stati compiuti grandi progressi nel settore dell'o. non lineare ultraveloce (impulsi di durata minore di 10 ps). Le intensità laser sono aumentate per più di quattro ordini di grandezza per raggiungere valori di 10²⁰ W/cm². Il campo elettrico associato a queste intensità è dell'ordine di 10¹² V/cm, cioè centinaia di volte il campo di Coulomb nell'atomo di idrogeno.

fig. 8A

La fig. 8A mostra i valori dell'intensità ottenuta da laser focheggiati nel corso degli ultimi anni. Dopo un iniziale aumento negli anni Sessanta, l'intensità raggiunse una saturazione per circa 20 anni a causa delle limitazioni imposte dagli effetti non lineari. Nell'ultima decade si è trovato il modo per superare queste difficoltà e l'intensità ha ricominciato a crescere. Il limite è dato dalla massima energia che è possibile immagazzinare nel materiale (quando si ha un'inversione completa di popolazione) diviso per la minima durata possibile dell'impulso (l'inverso della larghezza di banda del guadagno).

La tecnica della chirped pulse amplification (CPA) ha permesso di superare la principale difficoltà costituita dalla variazione dell'indice di rifrazione con l'intensità del fascio, che introduce 'effetti lente' che deformano il fascio e rendono impossibile il funzionamento oltre il limite dei gigawatt. Nella CPA, impulsi ultracorti non sono amplificati direttamente ma prima allungati nel tempo (in tal modo si diminuisce la potenza), poi amplificati e, finalmente, ricompressi. In questo modo è stato possibile usare mezzi attivi come il neodimio (Nd) in vetro, l'alessandrite, il titanio-zaffiro ecc., in cui l'immagazzinamento di energia è molto più alto che nei coloranti.

La fig. 8B mostra il concetto del CPA. Un oscillatore produce un impulso breve (per es. 100 fs) che è successivamente allungato per un fattore fra 1000 e 100.000, da femtosecondi a nanosecondi, riducendo la sua intensità. L'intensità è ora abbastanza bassa per poter amplificare l'impulso ed estrarlo dall'amplificatore senza distorsioni del fascio e senza danni. Dopo l'estrazione, l'impulso è ricompresso, idealmente alla sua durata originaria. Nella fig. 8C è mostrato il metodo per ottenere l'allungamento e la successiva ricompressione. Per allungare l'impulso si usano due reticoli antiparalleli. In questa disposizione, le lunghezze d'onda più lunghe (rosse) percorrono un cammino più breve di quelle corte (blu). In tal modo i raggi blu viaggiano più velocemente di quelli rossi: si ha una dispersione della velocità di gruppo negativa. Il compressore, invece, usa un paio di reticoli paralleli in cui la lunghezza ottica per i raggi blu è più corta di quella dei raggi rossi.

Gli impulsi ultracorti hanno uno spettro enorme, che per un impulso di 10 fs può essere 80 nm. Il titanio-zaffiro è un mezzo con una banda amplificante estremamente larga, che permette amplificazione anche su bande di 160 nm.

Per ottenere l'oscillatore a impulsi ultrabrevi sotto ai 10 fs si può usare il cosiddetto metodo KLM (Kerr Lens Modelocked), o bloccaggio dei modi con lente di Kerr utilizzando titanio-zaffiro. Il mezzo laser è pompato otticamente utilizzando, per es., un laser ad argo in continua. Il titanio-zaffiro funziona anche come una lente con lunghezza focale che dipende dall'intensità a causa della dipendenza del suo indice di rifrazione da quest'ultima. La cavità è progettata per funzionare in modo stabile per l'intensità più alta o per la durata più breve dell'impulso. Per ottenere l'impulso più breve la dispersione dell'impulso nel cristallo è compensata da specchi speciali (frequency-chirped mirrors), o da una sequenza di prismi.

La motivazione per usare impulsi ultracorti in un dato esperimento è data o dal desiderio di avere la risoluzione temporale necessaria per risolvere il processo d'interesse o per ottenere alte intensità di picco con impulsi di energia relativamente bassa. Attualmente si sono prodotti impulsi ottici della durata di meno di tre cicli nel visibile e nell'infrarosso, estendendo inoltre la regione spettrale dove questi possono essere ottenuti.

Dinamica non lineare ottica. - Negli ultimi anni, grandi progressi si sono avuti nel settore della dinamica non lineare ottica ove si considerano sistemi ottici non lineari che presentano instabilità temporali o spaziali: partendo da una condizione stazionaria il sistema può evolvere verso un dominio di instabilità periodico, quasi-periodico o caotico. La locuzione generica inizialmente usata per descrivere questi fenomeni tra gli anni Settanta e la metà degli anni Ottanta era bistabilità ottica.

Dall'inizio degli anni Ottanta vi è stato un rinnovato interesse per la dinamica dei laser, la dinamica non lineare dei fasci interagenti in mezzi non lineari e, in particolare, per la formazione di strutture spaziali e la dinamica spazio-temporale in molti tipi di interazioni non lineari tra luce e materia.

Le equazioni di funzionamento di un laser possono essere scritte:

Esse descrivono la dinamica della polarizzazione P e della popolazione (espressa tramite una differenza D di popolazione fra stato eccitato e stato fondamentale, opportunamente normalizzata) insieme a quella del campo elettrico E per un mezzo a due livelli. Le altre grandezze sono: k, che è proporzionale alla suscettività del mezzo; δ_AC = ω_A - ω_C, che indica la differenza fra la pulsazione del materiale e quella della cavità; A, che è una misura dell'interazione fra il mezzo e il campo elettrico; γ_P e γ_D, che sono le derivate temporali delle perdite (loss rate) di P e D rispettivamente. Queste sono le famose equazioni di Maxwell-Bloch del laser. Le soluzioni stazionarie sono rappresentate dall'equazione:

In unità normalizzate, A fornisce una misura dell'eccitazione del mezzo (cioè il tasso di pompaggio). Esistono soluzioni non banali solo per intensità positive per A>1+Δ² e l'intensità di queste soluzioni cresce linearmente con il parametro di pompa A. Quando si procede a un'analisi della stabilità di queste soluzioni stazionarie si trova che se k > γ_D + γ_P, esiste un valore di A oltre il quale gli stati stazionari sono instabili rispetto a piccole perturbazioni: si ottengono pulsazioni nella soluzione del singolo modo (caos di Lorenz).

fig. 9

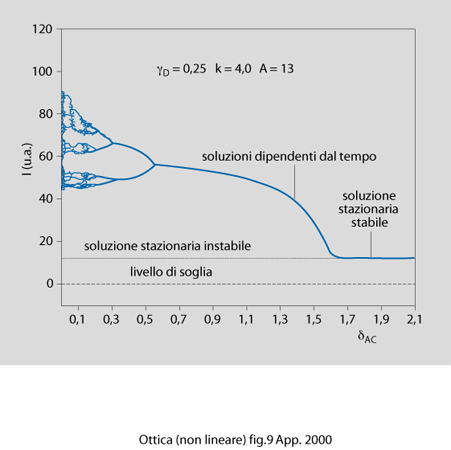
Se si mette il laser fuori risonanza (detuning) si scopre un comportamento più periodico. Un modo compatto di rappresentare le soluzioni è di disegnare i valori dell'intensità di picco in funzione del detuning, com'è mostrato nella fig. 9: dove i bracci delle biforcazioni sono indecisi vi è una serie caotica, aperiodica, di pulsazioni. Per grandi detuning il caos viene meno completamente e anche le pulsazioni scompaiono.

Questi risultati sono stati confermati da misure sperimentali con un laser ad ammoniaca. La varietà di pulsazioni rivela le sequenze di raddoppio del periodo (period-doubling) e le pulsazioni periodiche che si ripetono dopo un numero dispari di picchi d'intensità. Effetti simili si possono ottenere nelle strutture spaziali che possono venire rotte dalla formazione di variazioni spaziali. Per intensità più alte si possono avere pulsazioni di varie forme complesse.

fig. 10A

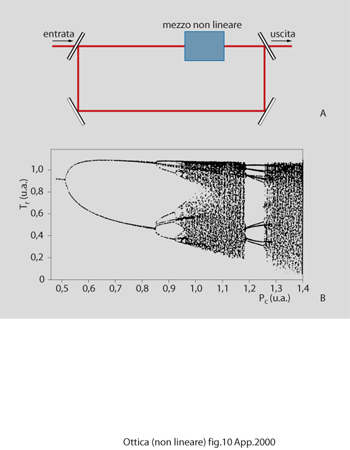
Caos e period-doubling sono stati trovati anche studiando sistemi bistabili. La fig. 10A mostra un sistema ad anello in cui si trova un materiale non lineare. Variando il detuning o l'intensità del campo varia la fase e quindi il ritardo fra i due campi che si propagano in direzioni opposte nel sistema, studiato per la prima volta da K. Ikeda nel 1979 e successivamente considerato da numerosi autori, utilizzando un gran numero di diversi materiali non lineari e vari metodi di ritardo. Ikeda trovò la possibilità di avere caos dinamico: la fig. 10B mostra dei risultati di simulazione. I valori ottenuti per un certo valore del tempo di ritardo sono mostrati sull'asse verticale e il valore di uno dei parametri di controllo è sull'asse orizzontale; per ogni valore del parametro di controllo, la natura della soluzione è rivelata dal numero di punti sulla corrispondente linea verticale. Un numero finito di punti indica una soluzione periodica. Una zona confusa indica una soluzione caotica irregolare. È possibile anche ottenere strutture spaziali complesse che emergono e si evolvono in sistemi ottici non lineari. I solitoni spaziali prima menzionati possono essere visti come un caso particolare di tali strutture.

Microcavità. - Il risonatore ottico, componente essenziale del laser e di altri dispositivi ottici, è caratterizzato da un insieme di modi, ciascuno con una frequenza di risonanza f e larghezza di risonanza δf=1/τ, dove τ è il tempo di vita di un fotone nel modo. Con i grandi sviluppi delle tecniche di deposizione, utilizzando per es. l'epitassia a fascio molecolare (MBE, Molecular Beam Epitaxy), è oggi possibile costruire cavità risonanti di dimensioni di pochi μm, confrontabili con la lunghezza d'onda della radiazione. Tali cavità, dette microcavità, hanno spesso la struttura di tipo Fabry-Pérot, e in esse le funzioni del dispositivo sono in gran parte simili a quelle di dispositivi più grandi, ma le piccole dimensioni le rendono particolarmente adatte alla selezione in lunghezze d'onda e alla concentrazione del campo ottico risonante, con suo conseguente aumento.

L'aumentato campo ottico permette, per es., di costruire fotorivelatori più sottili e quindi più veloci e contemporaneamente a più elevata efficienza quantica alle lunghezze d'onda risonanti, rendendoli particolarmente adatti per applicazioni in multiplexing a divisione di lunghezza d'onda. Modulatori ottici situati in una microcavità risonante richiedono meno pozzi quantici per assorbire la stessa frazione di luce incidente e possono di conseguenza operare a tensioni più basse. Nel caso di emettitori, la cavità modifica l'emissione spontanea dei diodi emettitori di luce (LED, Light-Emitting Diode), migliorando la loro purezza spettrale e direzionalità. Se si usa la microcavità per costruire un laser è possibile avere la soppressione dell'emissione spontanea o il suo aumento, come è stato studiato in microrisonatori tridimensionali superconduttori per microonde. Risonatori dielettrici cilindrici o sferici hanno risonanze con vite estremamente lunghe a causa dei modi whispering gallery in cui la luce circola lungo il perimetro, intrappolata da riflessione interna totale; questi risonatori emettono luce isotropicamente. Recentemente si è trovato che cavità asimmetriche di questo genere portano a una dinamica dei raggi parzialmente caotica.

Produzione di raggi X da armoniche. - Sorgenti coerenti di raggi X sono studiate per particolari applicazioni, tra cui la possibilità di osservare tridimensionalmente strutture biologiche microscopiche (per es. cellule e macromolecole) in vivo, utilizzando l'olografia a raggi X. Le sorgenti necessarie per questo tipo di applicazioni debbono presentare alta coerenza spaziale e una ragionevole coerenza temporale. Sorgenti X vengono ottenute mediante ondulatori magnetici in anelli di accumulazione di elettroni, o da plasmi generati da scariche laser con energie di molti kilojoule. Più recentemente si è iniziato a costruire e studiare sorgenti compatte di raggi X che sfruttano la generazione di armoniche di ordine molto elevato in gas.

Atomi ionizzati da un intenso campo elettrico di un impulso laser ultracorto possono emettere radiazione armonica coerente a energie dei fotoni molto maggiori dell'energia di legame dei loro elettroni. Per impulsi di durata dell'ordine di 100 fs si sono ottenute armoniche di ordini superiori a 100 con energie dei fotoni fino a 150 eV.

fig. 11A

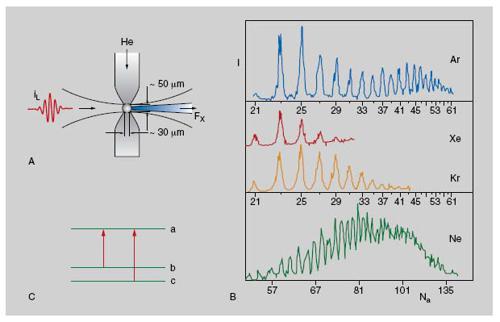
In modo schematico, il processo può essere spiegato come un'interazione a singolo fotone. In un primo momento, l'elettrone attraversa per effetto tunnel la barriera di potenziale coulombiano atomico, ridotta dall'intenso campo elettrico. L'elettrone quasi libero acquista poi energia cinetica dal campo laser e, quando il campo s'inverte, viene rinviato verso il suo ione. Con una probabilità invero non molto alta l'elettrone si ricombina con lo ione parente, emettendo un fotone la cui energia è pari a quella di ionizzazione dell'atomo più l'energia cinetica guadagnata sotto l'azione del campo laser. Il processo è ripetuto periodicamente in molti cicli di un impulso e dà luogo all'emissione di armoniche della radiazione incidente. Una disposizione sperimentale è mostrata in fig. 11A. Un sottile fascio di atomi di un gas nobile (per es. elio, He) è fatto passare attraverso un tubo con una piccola apertura su cui è focheggiato l'impulso laser. Il fascio di raggi X coerenti è emesso in modo direzionale nella direzione di propagazione dell'impulso incidente. La fig. 11B mostra uno spettro ottenuto sperimentalmente. Gli impulsi X prodotti in un fascio, le cui caratteristiche sono al limite della diffrazione, offrono ora la potenzialità per ottenere impulsi di durata dell'attosecondo.

Raffreddamento di atomi. - Il raffreddamento di un gas atomico mediante laser fu proposto nel 1975 da T. Haensch e A. Schawlow. Lo stesso anno D. Wineland e H. Dehmelt suggerirono uno schema simile per raffreddare ioni. Il principio del raffreddamento laser (v. fisica atomica, in questa Appendice) si basa sul trasferimento di quantità di moto da un fotone a un atomo che lo assorbe.

L'atomo riceve un impulso nella direzione in cui il fotone si propaga. La successiva riemissione di un fotone dall'atomo, per la conservazione della quantità di moto, produce un rinculo, ma, se l'emissione è spontanea, la direzione del fotone emesso è distribuita a caso. Una serie di processi di assorbimento ed emissioni trasferisce quantità di moto all'atomo nella direzione del fascio di luce, mentre il rinculo si media a zero. Il risultato è che un atomo che si propaghi contro un fascio di luce è rallentato. Il metodo consiste nell'aggiustare la frequenza del fascio laser un poco al di sotto di quella necessaria per l'assorbimento. In questo modo un atomo fermo non assorbe, ma un atomo che si muova verso il fascio, a causa dell'effetto Doppler, 'vede' la frequenza del fascio spostata verso la sua riga di assorbimento e la assorbe. Usando più fasci laser è possibile rallentare gli atomi. Nel 1985 S. Chu (premio Nobel nel 1997 insieme a C. Cohen-Tannoudji e W. Phillips per lo sviluppo di metodi per raffreddare e intrappolare atomi mediante luce) usò sei fasci laser a coppie ortogonali per raffreddare circa un milione di atomi di sodio. Per raffreddare gli atomi, ogni fascio laser deve esercitare una forza solo su quegli atomi che si muovono in direzione opposta. Questi atomi sono automaticamente selezionati perché solo loro hanno un effetto Doppler sufficiente per permettere l'assorbimento: il risultato è che gli atomi vengono rallentati in qualunque situazione si muovano. L'effetto è simile a quello che essi proverebbero muovendosi in una forza viscosa, e Chu indicò questo campo 'viscoso' col nome di melassa ottica.

La tecnica di raffreddamento e intrappolamento degli atomi è stata essenziale per la dimostrazione nel 1995 della condensazione di Bose-Einstein. Chu e collab. hanno mostrato che colpendo degli atomi raffreddati con un fascio laser è possibile farli uscire dalla trappola; un fatto estremamente importante è che, misurando il tempo che gli atomi impiegano a salire in alto e poi ricadere in una 'fontana atomica', si ottiene la misura più precisa possibile della gravità terrestre mai fatta. Una fontana simile permette inoltre di costruire un orologio atomico caratterizzato da una precisione di 10⁻¹⁶.

Laser senza inversione. - Nei laser ordinari, per avere l'emissione è necessario provocare un'inversione di popolazione. Nel 1988 diversi autori avanzarono l'idea che in linea di principio fosse possibile avere azione laser senza inversione sfruttando effetti di interferenza quantistica, e negli anni Novanta si sono ottenuti i primi risultati sperimentali: il metodo consiste nell'estrarre energia da atomi eccitati anche se ci sono più atomi nel livello inferiore.

Per comprendere come questo sia possibile, si consideri (fig. 11C) un atomo in cui il campo laser sia accoppiato a due livelli invece che a uno solo. Supponiamo che questo atomo sia preparato in una 'sovrapposizione coerente' dei due livelli più bassi ∣b 〉 e ∣c 〉; le ampiezze di probabilità complessa per l'assorbimento della luce dai livelli ∣b 〉 o ∣c 〉 al livello superiore ∣a 〉 sono A_ab e A_ac. Per trovare la probabilità totale di assorbimento da questa sovrapposizione coerente è necessario sommare le ampiezze e poi fare il quadrato poiché si termina a uno stato comune. Questo dà luogo a un termine d'interferenza che in certe condizioni fa sì che la probabilità di assorbimento vada a zero. D'altro lato, la probabilità di emissione da un atomo nel livello superiore è proporzionale alla somma dei quadrati ∣A_ab∣² e ∣A_ac∣².

I metodi per realizzare sperimentalmente la situazione dei livelli descritta sono molteplici e complicati. A tutt'oggi è stata dimostrata solo la possibilità di amplificazione.

Ottica quantistica. - Altri aspetti fondamentali connessi con le non linearità del secondo e terzo ordine sono quelli legati all'o. quantistica, in particolare la riduzione del rumore quantico attraverso amplificazione parametrica e l'oscillazione e generazione di stati squeezed (v. oltre: Rumore quantistico in ottica).

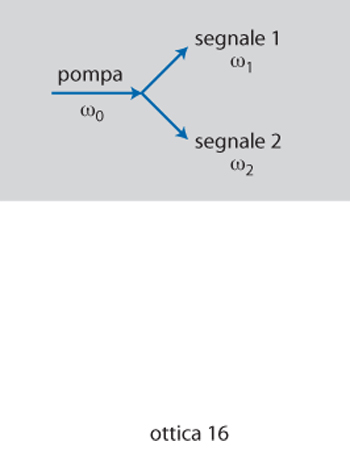
I fenomeni del second'ordine rappresentano anche un mezzo utile per l'indagine sperimentale di questioni ancora dibattute in meccanica quantistica, come lo studio degli stati entangled a due particelle degli esperimenti, sul tipo di quello suggerito da Einstein-Podolsky-Rosen, in cui la misura di una osservabile di una particella determina il valore di quella osservabile per l'altra particella con probabilità unitaria. Alla fine degli anni Ottanta la down conversion spontanea parametrica emerse come un utile mezzo per studiare stati entangled di due particelle. Nella SODC (Spontaneous Optical Down Conversion) solo un fascio di pompa è incidente su un cristallo non lineare quadratico e si genera una coppia di fotoni altamente correlati nello spazio delle fasi perché soddisfano la conservazione dell'energia ω_s = ω_i + ω_p e la conservazione del momento k_s = k_i + k_p (condizione di accordo di fase), dove ω e k rappresentano le pulsazioni e i vettori d'onda del segnale (s), idler (i) e pompa (p). La condizione di conservazione dell'energia e del momento dei fotoni coinvolti nel processo non lineare porta alla creazione di uno stato entangled quantico della coppia di fotoni generato durante il processo.

bibliografia

P.N. Butcher, D. Cotter, The elements of nonlinear optics, Cambridge-New York 1990.

R.W. Boyd, Nonlinear optics, Boston 1992.

Molecular nonlinear optics: materials, physics, and devices, ed. J. Zyss, Boston 1994.

D.L. Mills, Nonlinear optics: basic concepts, New York 1998.

Rumore quantistico in ottica

di Luigi Alberto Lugiato, Alice Sinatra

Il concetto di rumore quantistico fa parte dei concetti fondamentali che costituiscono il cuore della teoria quantistica della fisica. La natura intrinsecamente probabilistica della meccanica quantistica è implicata dalle regole di indeterminazione di Heisenberg, che pongono un limite al grado di informazione che possiamo ricavare sullo stato di un sistema fisico stabilendo che, nel corso di una misura di due variabili coniugate (come la posizione e il momento di una particella), il prodotto delle incertezze minime su queste variabili non può essere inferiore a una quantità dell'ordine di grandezza della costante di Planck h. In questo senso si può dire che le fluttuazioni quantistiche 'siano' la meccanica quantistica piuttosto che un aspetto o una manifestazione di quest'ultima.

L'esempio più semplice di rumore quantistico ci è offerto da uno dei sistemi più studiati in fisica: l'oscillatore armonico unidimensionale. L'Hamiltoniana (l'energia) di questo sistema è costituita dalla somma dell'energia cinetica e dell'energia potenziale e ha la forma:

dove x è la posizione, p è la quantità di moto, m è la massa e ω/(2π) è la frequenza dell'oscillatore. Lo stato quantistico fondamentale (cioè quello con il valore di energia più basso) di questo sistema ha energia E₀=(1/2)ℏω, con ℏ=h/(2π), maggiore di zero; un'energia totale uguale a zero è infatti proibita dal principio di indeterminazione di Heisenberg. Essendo l'energia una forma quadratica e positiva nella posizione e momento dell'oscillatore, un'energia nulla si ottiene solo se x=0 e contemporaneamente p=0, il che implicherebbe avere simultaneamente un'informazione precisa sulla posizione e sulla quantità di moto, contrariamente alla regola di indeterminazione che stabilisce:

formula

[1]

dove Δx e Δp sono le incertezze, o più propriamente le varianze di posizione e momento, individuate dalla relazione (ΔA)²=〈A²〉−〈A〉², dove 〈A〉 indica la media su molte misure della grandezza A eseguite su sistemi identici e preparati nello stesso modo. Di fatto, nello stato fondamentale, la posizione e la quantità di moto dell'oscillatore sono descritte da distribuzioni di probabilità gaussiane centrate sul valore zero, e con larghezze tali che Δx∙Δp=ℏ/2. Questo significa che i valori medi di posizione e quantità di moto dell'oscillatore sono nulli, ma entrambe le grandezze sono affette da fluttuazioni casuali attorno al valore medio (che in questo caso soddisfano la [1] con il segno di uguaglianza, e per questo motivo lo stato del sistema viene detto a minima indeterminazione): tali fluttuazioni costituiscono il rumore quantistico.

Una situazione molto diversa è quella descritta dalla fisica classica. L'energia minima di un oscillatore classico è esattamente zero, corrispondentemente alla situazione in cui l'oscillatore è in quiete (energia cinetica nulla) nell'origine (energia potenziale nulla). Ciò nondimeno il concetto di rumore è comune nella fisica classica che descrive i sistemi macroscopici. In quel contesto, il rumore proviene dalle limitazioni che abbiamo nel controllare tutti i gradi di libertà del sistema. Il rumore termico, per es., è legato alla difficoltà di controllare le variabili microscopiche (come le posizioni e le velocità di ciascun atomo in un gas), mentre il rumore parametrico è legato alla precisione finita con la quale lo sperimentatore può fissare i parametri del sistema. Il rumore quantistico è sostanzialmente diverso da tutti questi tipi di rumore classico. La differenza più importante risiede nel fatto che per la sua natura intrinseca, legata al principio di indeterminazione di Heisenberg, esso non può essere mai completamente soppresso. In altre parole, non esiste alcuno stato quantistico che sia privo di fluttuazioni in tutte le sue osservabili (grandezze misurabili). Al contrario, il rumore classico può essere ridotto ad libitum impiegando tecniche sperimentali sempre più raffinate. Per es. il rumore termico può essere eliminato portando teoricamente il sistema alla temperatura dello zero termodinamico; nel caso del rumore parametrico, lo sperimentatore può usare la sua abilità (inserendo dei circuiti di controllo ecc.) per ridurlo al disotto del livello desiderato. È interessante notare che attualmente il livello tecnologico e le tecniche sperimentali permettono di ridurre il rumore classico a tal punto che le piccole fluttuazioni quantistiche possono essere osservate. In questa situazione il limite fondamentale sul controllo di un sistema e quello sull'accuratezza di una misura derivano proprio dal rumore quantistico.

Il fatto che il rumore quantistico non possa essere interamente soppresso non implica fortunatamente che esso non possa essere evitato in qualsiasi tipo di misurazione. Il principio di indeterminazione di Heisenberg impedisce infatti di ridurre le fluttuazioni quantistiche contemporaneamente in due variabili coniugate, dato che la regola di Heisenberg riguarda il prodotto delle fluttuazioni nelle due variabili, ma non impedisce che si possa ridurre a piacere il rumore quantistico in una singola osservabile che si prenda in considerazione. Naturalmente, riducendo arbitrariamente le fluttuazioni in un'osservabile si aumentano necessariamente le fluttuazioni nell'osservabile coniugata. Quest'ultimo aspetto rappresenta la seconda differenza tra rumore classico e rumore quantistico. Infatti, mentre in un sistema classico la riduzione delle fluttuazioni in una variabile è generalmente accompagnata da una riduzione del rumore in tutte le altre variabili, in un sistema quantistico ciò non accade: proprio per aver ridotto le fluttuazioni in una variabile, otteniamo delle fluttuazioni aumentate nella variabile coniugata; e questo è necessario affinché le regole di indeterminazione di Heisenberg siano soddisfatte.

Queste considerazioni hanno portato, alla fine degli anni Settanta, alla nascita della riduzione del rumore quantistico o squeezing e delle misure quantistiche non distruttive (QND, Quantum Nondemolition). L'idea dello squeezing, come suggerisce il nome, che vuol dire 'strizzamento' o 'schiacciamento', è che lo stato quantistico, o meglio le sue fluttuazioni, si comportino come una palla di gomma piena d'aria che, compressa in una direzione, si espande nella direzione ortogonale. Un sistema squeezed è dunque un sistema dove si sono ridotte le fluttuazioni in una variabile a spese delle fluttuazioni nella variabile coniugata. Più precisamente, uno stato del sistema viene definito squeezed quando esiste una determinata osservabile per cui le fluttuazioni siano al di sotto di un livello di riferimento, determinato dagli stati coerenti dell'oscillatore armonico (v. oltre).

L'idea delle misure quantistiche non distruttive è invece legata più espressamente al procedimento di misurazione di una grandezza in un sistema quantistico. Per introdurre l'idea, consideriamo dapprima la seguente esperienza ideale. Immaginiamo di effettuare una misurazione estremamente accurata della posizione di una particella libera (non soggetta a forze). Per il principio di Heisenberg, ovvero per le proprietà dei sistemi quantistici, una buona determinazione e dunque piccole fluttuazioni nella posizione della particella implicano necessariamente grandi fluttuazioni nella variabile coniugata che è la quantità di moto della stessa. D'altra parte, la quantità di moto della particella libera a un dato istante determina la sua posizione negli istanti successivi, e dunque l'incertezza nella quantità di moto della particella, introdotta dalla determinazione accurata della posizione, si rifletterà nei tempi seguenti in una incertezza sulla posizione che dunque vanificherà i nostri sforzi di misurazione. In altre parole, a causa della presenza delle fluttuazioni quantistiche, l'informazione precisa che abbiamo acquisito è resa inutile dalla misurazione stessa, per cui una seconda misurazione di un'osservabile compiuta immediatamente dopo la prima, fornisce in generale un risultato diverso dalla prima. Al contrario dell'esperienza appena descritta, una misura quantistica non distruttiva è concepita in modo tale da non introdurre rumore nella variabile di interesse, cosicché misurazioni successive della variabile stessa diano sempre lo stesso risultato entro l'accuratezza sperimentale. Per raggiungere questo scopo è necessario che la variabile di interesse non dipenda in alcun modo dalla variabile coniugata, che invece deve raccogliere tutto il rumore introdotto nel sistema quando effettuiamo la misurazione, senza giocare alcun ruolo negativo.

Ridurre le fluttuazioni quantistiche in un'osservabile di un sistema quantistico a spese delle fluttuazioni nell'osservabile coniugata, o inventare delle misure che aggirino il rumore 'nascondendolo' in una variabile non interessante, sono ora esperienze realizzabili nei laboratori di o. quantistica.

Ciò che chiamiamo luce (propriamente pura) è descritto in fisica come un'onda formata da un campo elettrico e un campo magnetico propagantisi in una certa direzione, e oscillanti alla pulsazione ω≃10¹⁵ rad s⁻¹.

Consideriamo un'onda stazionaria, linearmente polarizzata, di pulsazione ω che si propaga lungo l'asse z in una cavità lineare delimitata da due pareti riflettenti poste a una distanza L l'una dall'altra. Il campo elettrico E e il campo magnetico B che compongono l'onda dipendono dal tempo t e dalla posizione z nella cavità. Introducendo due funzioni del tempo p(t) e q(t), si possono rappresentare i campi come:

formula [

2]

dove k=ω/c=2π/λ è il vettore d'onda (c è la velocità della luce nel vuoto), determinato dalla condizione che 2L sia un multiplo intero della lunghezza d'onda, Eo e Bo sono costanti dove compaiono la pulsazione ω, il volume V della cavità e la costante dielettrica nel vuoto εo: Eo=(2ω²/εoV)¹^/², Bo=(2/εoc²V)¹^/², e le funzioni q(t) e p(t) sono determinate dalle equazioni di Maxwell senza sorgenti che descrivono la propagazione di un campo elettromagnetico nel vuoto. Ciò implica che le funzioni introdotte q(t) e p(t) abbiano la stessa dipendenza dal tempo delle variabili posizione e quantità di moto di un oscillatore armonico di massa unitaria. Inoltre, usando la parametrizzazione [2] dei campi funzioni del tempo q(t) e p(t) l'energia totale dell'onda stazionaria nel volume V assume la forma particolare:

identica all'energia di un oscillatore armonico con massa uguale a 1. In questo senso il modo del campo elettromagnetico corrispondente all'onda stazionaria è equivalente a un oscillatore armonico. Considerando un oscillatore quantistico, otteniamo quindi semplicemente la descrizione quantistica del campo elettromagnetico. La prima differenza importante introdotta dalla descrizione quantistica del nostro sistema riguarda le energie permesse al campo. Nel caso quantistico l'energia non può assumere tutti i valori ma è limitata a un insieme discreto di livelli E_n=(n+1/2)ℏω enumerati da un indice n che assume valori interi. L'energia minima ottenuta per n=0 è E₀=ℏω/2, mentre le successive energie si ottengono assegnando a n i valori 1, 2, 3, … ecc. Nella formula delle energie E_n, l'intero n rappresenta il numero di quanti di eccitazione o fotoni nel modo. Lo stato fondamentale dell'oscillatore, corrispondente a n=0, o zero fotoni, è detto stato di vuoto nel campo elettromagnetico.

Usando le notazioni introdotte da P.A.M. Dirac, gli autostati ∣n〉 dell'energia sono definiti dall'equazione

e vengono detti stati a n fotoni. Risulta conveniente introdurre le osservabili adimensionali

formula [

3]

cosicché per es.

formula [

4]

avendo preso

Gli operatori

formula [

5]

dove ‡ indica l'aggiunto dell'operatore, sono chiamati, rispettivamente, operatori di annichilazione e di creazione di fotoni, perché si dimostra che

L'operatore a diminuisce il numero di fotoni di una unità, mentre a‡ lo aumenta di una unità. Dalle equazioni [4] e [5] si ha che

formula [

6]

Il secondo aspetto importante legato alla descrizione quantistica riguarda invece le fluttuazioni alle quali sono soggette le variabili del sistema, nel nostro caso i campi. Dato che nella descrizione quantistica, q(t) e p(t) soddisfano la regola di indeterminazione di Heisenberg, Δq∙Δp≥ℏ/2, una simile relazione è soddisfatta dai campi elettrico e magnetico della luce che quindi non possono essere specificati contemporaneamente in un dato istante con accuratezza arbitraria. Anche nello stato di vuoto, in cui i valori medi dei campi E e B sono nulli, i campi elettrico e magnetico sono soggetti alle fluttuazioni quantistiche attorno al valore medio in modo tale che le loro varianze ΔE e ΔB soddisfino il principio di indeterminazione. In particolare, l'ordine di grandezza della varianza del campo elettrico nello stato di vuoto è dato dalla quantità Eo=(ℏ/εoV)¹^/², detta campo elettrico per fotone: per es., per il modo in cui si ha processo laser di un laser elio-neon si ottiene per tale quantità il valore Eo≃10⁻² V∙m⁻¹, che mostra come le fluttuazioni quantistiche non siano affatto trascurabili in alcuni casi. Le fluttuazioni quantistiche dei campi nello stato di vuoto sono responsabili di molti importanti fenomeni, come l'emissione spontanea di un atomo, il Lamb shift e l'effetto Casimir. Riuscire a controllare le fluttuazioni quantistiche del vuoto ci permetterebbe di modificare conseguentemente questi effetti fondamentali oltre ad aprire nuove strade, come vedremo, nel campo delle misure di altissima precisione che utilizzano l'ottica.

Stati coerenti e stati squeezed

Dalle equazioni per l'oscillatore armonico, è semplice dimostrare che l'evoluzione temporale di a(t), a(t)‡ è data dalla relazione

cosicché usando le [6] e le [5] otteniamo

formula [

7]

formula [

8]

fig. 12

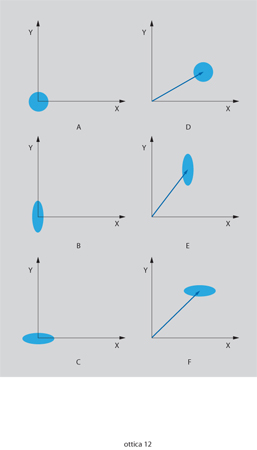
ove abbiamo posto X≡X(0), Y≡Y(0). Le grandezze X, Y sono dette quadrature del campo elettromagnetico; precisamente, X e Y sono dette componenti in fase e in quadratura del campo elettrico, rispettivamente. Dalla regola di indeterminazione di Heisenberg Δx∙Δp≥ℏ/2 e dalla [3] otteniamo che deve essere verificata la relazione ΔX∙ΔY≥1/4. Utilizzando le quadrature, possiamo descrivere pittoricamente gli stati del campo elettromagnetico, nel modo mostrato in fig. 12. Ogni stato è rappresentato da un vettore che punta sul valore medio 〈X〉 e 〈Y〉 delle quadrature X e Y, e da un'ellisse che rappresenta l'incertezza sul valore esatto di ciascuna quadratura, quantificata dalle varianze ΔX e ΔY.

Gli stati quantistici del campo elettromagnetico che si avvicinano di più agli stati classici sono gli stati coerenti, definiti come autovettori dell'operatore di annichilazione a:

fig. 13

Si dimostra che qualsiasi numero complesso α è un autovalore dell'operatore a. In fig. 12A e D abbiamo rappresentato due esempi di stato coerente. In questi stati, tra i quali figura lo stato di vuoto del campo (quello corrispondente ad α=0), le varianze delle due quadrature sono uguali tra loro e sono tali da soddisfare le condizioni di minima indeterminazione ΔX∙ΔY=1/4, per cui ΔX^c°^er=ΔY^c°^er=1/2. D'altra parte, esistono stati del campo tali che ΔX〈1/2 (per cui necessariamente ΔY>1/2) oppure ΔY〈1/2 (per cui ΔX>1/2); questi sono detti stati schiacciati o squeezed. In fig. 12B, C, E, F troviamo alcuni esempi di stati squeezed. Le equazioni [7] e [8] mostrano come, durante l'evoluzione temporale, E(t) e B(t) si 'scambino' periodicamente le proprietà quantistiche legate alle quadrature. Supponiamo, per es., che ΔX(0)〈ΔX^c°^er e ΔY(0)>ΔY^c°^er: all'istante t=0 il campo elettrico mostra fluttuazioni quantistiche ridotte, ma dopo un quarto di periodo sarà il campo magnetico ad avere fluttuazioni ridotte, mentre le fluttuazioni nel campo elettrico saranno aumentate. In questo senso lo squeezing è un fenomeno dipendente dalla fase: si osservano fluttuazioni ridotte nel campo elettrico soltanto per certi tempi, o meglio per certi valori della fase che evolve periodicamente alla frequenza ottica. In fig. 13 abbiamo rappresentato nello spazio delle quadrature tre stati del campo all'istante t=0: uno stato coerente e due stati in cui, rispettivamente, X(0) o Y(0) hanno fluttuazioni ridotte rispetto allo stato coerente. Tenendo conto del fatto che per i casi mostrati in fig. 13 risulta 〈Y〉=0 e che le variabili X e Y sono scorrelate dall'equazione [7] otteniamo le seguenti relazioni:

.

Sotto ciascun diagramma nello spazio delle quadrature abbiamo quindi rappresentato l'evoluzione temporale del campo elettrico. La linea piena centrale indica il valore medio dell'ampiezza del campo elettrico, mentre la zona in colore compresa tra le due linee piene esterne rappresenta le fluttuazioni attorno al valore medio. Notiamo innanzi tutto che nel caso dello stato coerente (A) (per cui ΔX=ΔY=1/2) le fluttuazioni non dipendono dalla fase ωt del campo, mentre esse dipendono sinusoidalmente dalla fase nei casi squeezed (B) e (C). Nel caso (B), in cui la quadratura X(0) ha fluttuazioni ridotte, osserviamo che l'ampiezza del campo (data dal valore massimo E(t) durante un periodo) è ben definita, mentre la fase (determinata dal punto in cui E(t) cambia segno) è mal determinata. Nel caso (C) avviene esattamente l'opposto. Alla stessa conclusione si arriva in modo più intuitivo partendo da grafici come quelli in alto in fig. 13, ma facendo corrispondere agli assi cartesiani le due quantità E(t,kz=π/2)/(2Eo) e B(t,kz=0)/(2ℬo) invece di X(0) e Y(0), rispettivamente. In questo caso il vettore che rappresenta i valori medi ruota nel tempo con pulsazione ω, e corrispondentemente ruota l'ellisse; dalla rotazione si vede immediatamente come varia nel tempo la varianza di E.

Regime linearizzato delle fluttuazioni

In molti casi le fluttuazioni quantistiche sono piccole rispetto ai valori medi dei campi e possono essere trattate nell'approssimazione lineare, che consiste nello scomporre le quadrature nel loro valore medio più le fluttuazioni quantistiche a media nulla: X(t)=〈X〉+δX, Y(t)=〈Y〉+δY, trattando le fluttuazioni come quantità piccole. In quest'approssimazione le fluttuazioni nell'intensità della luce o nel numero di fotoni n nel modo sono semplicemente proporzionali alle fluttuazioni nella quadratura ampiezza. Precisamente, nei casi in cui 〈Y〉=0, si trova

e una relazione analoga vale per le varianze:

La varianza ΔX(0)=1/2 degli stati coerenti corrisponde dunque a una varianza poissoniana nel numero dei fotoni: Δn/〈n〉=1/(〈n〉)¹^/², che mostra come le fluttuazioni quantistiche nel numero di fotoni siano 'piccole' rispetto al valore medio se tale valore medio è grande. Una varianza ΔX(0)〈1/2 darà luogo a fluttuazioni quantistiche nel numero di fotoni minori di quelle poissoniane: Δn/〈n〉〈1/(〈n〉)¹^/².

Proprietà statistiche della luce

Le fluttuazioni nel numero di fotoni di un campo possono essere rivelate in un esperimento, per es. inviando la luce a un fotomoltiplicatore e osservando la statistica dei fotoelettroni emessi o, per un campo intenso, le fluttuazioni prodotte nella corrente all'uscita del fotomoltiplicatore. Le fluttuazioni poissoniane del numero di fotoni in uno stato coerente, comunemente emesso da un laser ben sopra soglia, danno origine a un rumore della corrente indipendente dalla frequenza, detto shot noise. D'altra parte esistono stati, come gli stati squeezed della quadratura ampiezza, che presentano fluttuazioni nel numero di fotoni ridotte rispetto a quelle poissoniane col risultato che per questi stati le fluttuazioni della corrente in un intervallo opportuno di frequenze sono ridotte al di sotto dello shot noise.

Storicamente, gli esperimenti volti a misurare le proprietà statistiche della luce, come la varianza dell'intensità luminosa ΔI o la funzione di autocorrelazione temporale 〈I(t)I(t+τ)〉, ebbero un ruolo importante nella storia dell'o. e della fisica quantistica. Furono infatti esperimenti di questo tipo, come la misura della funzione di correlazione della luce di fluorescenza di un singolo atomo eccitato da luce laser accordata con la frequenza di una transizione atomica, a provare in modo inequivocabile la natura quantistica della radiazione luminosa.

Per comprendere meglio come le proprietà quantistiche della luce possano essere evidenziate in un esperimento e per introdurre un vasto capitolo dell'o. quantistica che classifica stati classici e stati non classici della luce, consideriamo la seguente esperienza: su un fotomoltiplicatore incida un fascio di luce monocromatico di intensità Io costante nel tempo, 'classica', ossia senza fluttuazioni quantistiche. In questa situazione, il numero medio di conteggi di fotoelettroni collezionati in un certo intervallo di tempo T è direttamente proporzionale all'intensità Io e all'intervallo di tempo T con una costante di proporzionalità che dipende dalle caratteristiche del rivelatore: n̄=ξIoT, e in ogni intervallo di tempo infinitesimo dt esiste una probabilità costante pari a ξIodt che venga emesso un fotoelettrone. Tutte le informazioni sulla statistica dei fotoelettroni (e indirettamente della luce) sono accessibili conoscendo la distribuzione P(n,T) rappresentante la probabilità che vengano emessi esattamente n fotoelettroni nell'intervallo di tempo T. Nel nostro caso semplice di intensità costante la distribuzione P(n,T) è una distribuzione di Poisson e la varianza del numero di fotoelettroni collezionati in un intervallo di tempo T è poissoniana: Δn= n̄.

Consideriamo ora il caso più generale in cui l'intensità della luce non sia costante ma abbia delle fluttuazioni regolate da una certa distribuzione di probabilità stazionaria P(I), con I=ℏωn, e chiamiamo Io l'intensità media: Io=∫dIIP(I). Un risultato importante della teoria della fotorivelazione mostra che la varianza del numero di fotoelettroni collezionati nell'intervallo di tempo T piccolo rispetto ai tempi caratteristici delle fluttuazioni dell'intensità, è data dalla relazione:

formula [

9]

dove per brevità abbiamo indicato la media sulla distribuzione di probabilità P(I) con il simbolo 〈〉_P(I). Nel caso senza fluttuazioni: I=Io, ritroviamo il risultato che il numero di conteggi in un intervallo T ha una varianza poissoniana. D'altra parte, essendo la quantità (I−Io)² positiva, una qualsiasi distribuzione di probabilità classica P(I) (necessariamente definita positiva) darà luogo a una varianza maggiore di quella poissoniana.

Nella realtà tuttavia la varianza Δn, che risulta poissoniana per uno stato coerente della luce, può essere inferiore a una varianza poissoniana per alcuni stati quantistici, tra i quali per es. gli stati squeezed nella quadratura ampiezza, che abbiano la proprietà di avere delle fluttuazioni sub-poissoniane nel numero di fotoni: Δn/〈n〉〈1/(〈n〉)¹^/². Questo significa che volendo per convenienza rappresentare le fluttuazioni del campo elettromagnetico come fluttuazioni di intensità descritte da una certa distribuzione di probabilità P(I), si devono introdurre necessariamente delle distribuzioni denominate di quasi probabilità non necessariamente positive. Gli stati della luce per i quali la distribuzione di quasi probabilità non è positiva vengono comunemente detti stati non classici della luce.

Usando le distribuzioni di quasi probabilità è possibile esprimere la media di una grandezza di un sistema quantistico tramite un integrale con la distribuzione di quasi probabilità dall'apparenza classica. Ci limiteremo a menzionare la distribuzione di quasi probabilità associata alla descrizione degli stati quantistici fornita dalla rappresentazione introdotta da R. Glauber e G. Sudarshan, basata sugli stati coerenti. Usando tale rappresentazione si può esprimere la media quantistica di una funzione f degli operatori a‡ e a semplicemente come media classica calcolata su di una distribuzione di quasi probabilità P(α,α*), della funzione f(α*,α) ottenuta da f(a‡,a) sostituendo agli operatori a‡ e a delle variabili numeriche: a→α, a^†→α*, dove il simbolo * indica il complesso coniugato. In formule:

Perché la formula sia valida è necessario tuttavia che gli operatori a^† e a compaiano nella funzione f nell'ordine normale, cioè con tutti gli operatori di creazione alla sinistra degli operatori di annichilazione, il che è simboleggiato nella formula dai due puntini ::.

Nel contesto di una teoria quantistica della fotorivelazione, usando la rappresentazione di Glauber e Sudarshan, è possibile esprimere la varianza del numero di fotoni per un campo di luce quantistico, in maniera del tutto analoga alla [9] valida per un campo classico. In questo caso infatti si ha:

dove 〈〉_P₊_α,_α*₋ indica il valore medio calcolato sulla distribuzione P(α,α*). La linea di demarcazione tra stati classici e stati non classici del campo elettromagnetico è segnata dagli stati coerenti ∣αo〉, per i quali la P(α) è una distribuzione delta di Dirac: P(α,α*)=δ(α−αo)δ(α*−αo*).

Si può dimostrare che lo stato coerente ∣α〉 è ottenuto dallo stato fondamentale ∣0〉 nel modo seguente

dove D(α) è l'operatore D(α)=exp(aa‡). È possibile definire degli stati che, come quelli coerenti, sono a minima indeterminazione, ma sono squeezed in una componente in quadratura. Questi stati sono caratterizzati da due indici complessi α e ξ e sono ottenuti attraverso l'operatore D(α) nel modo seguente

formula [

10]

L'applicazione dell'operatore S(ξ) allo stato di vuoto ∣0〉 genera uno stato di vuoto squeezed come quelli mostrati in fig. 12B e C; l'applicazione dell'operatore D(α) conduce a uno stato squeezed del tipo di quelli in fig. 12E ed F. Variando la fase del numero complesso ξ, si controlla la quadratura in cui si ha squeezing.

La struttura dell'operatore di squeezing, data dalla [10] come esponenziale di una forma quadratica in a e a‡, mostra che gli stati squeezing possono essere generati da processi caratterizzati da un'hamiltoniana quadratica negli operatori a e a‡. Un sistema di questo tipo è l'amplificatore parametrico degenere, in cui l'hamiltoniana di interazione è

formula [

11]

fig. 14A

dove a₀ e a₁ sono, rispettivamente, gli operatori di annichilazione di fotoni del campo di pompa di pulsazione ω₀ e del campo di pulsazione ω₁=ω₀/2, e g è la costante d'accoppiamento. La [11] descrive processi non lineari in cui un fotone del campo di pompa viene convertito in una coppia di fotoni del campo segnale, e viceversa. Nell'amplificatore parametrico si inietta nel campione un forte campo di pulsazione ω₀ (fig. 14A); quando il campione è contenuto in una cavità ottica si ha un oscillatore parametrico (fig. 14B). Per comprendere il funzionamento dell'amplificatore, assumiamo che il campo di pompa sia così intenso da poter essere considerato un campo classico e da poter trascurare l'impoverimento del numero di fotoni di pulsazione ω₀ dovuto alla generazione di fotoni di pulsazione ω₀/2. In tali condizioni l'operatore a₀ può essere sostituito da un numero complesso costante α^*₀, cosicché la [11] diventa

formula [

12]

e ha esattamente la forma dell'esponente nell'operatore di squeezing [10]. In quest'approssimazione, la propagazione del valore medio 〈a₁〉 del campo segnale nella direzione z del campione (fig. 14A) nello stato stazionario è descritta dall'equazione

dove v è la velocità di propagazione del campo segnale nel mezzo. Pertanto, introducendo le quadrature

fig. 15

Supponiamo, per fissare le idee, che la costante α₀ sia reale e positiva. Se in ingresso si inietta, oltre al campo di pompa α₀, anche un debole campo segnale, dalla [13] vediamo che la componente in quadratura X viene amplificata durante la propagazione nel campione, mentre la componente Y è corrispondentemente attenuata. La situazione più interessante sorge però in assenza di segnale in ingresso o, più precisamente, quando il campo segnale in ingresso è nello stato di vuoto. Le fluttuazioni del vuoto vengono amplificate per una quadratura e attenuate per l'altra, esattamente come descritto per il caso di un debole campo segnale classico in ingresso. Poiché l'amplificazione e l'attenuazione avvengono nella stessa misura, lo stato coerente (in ingresso) si trasforma in uno stato squeezed a minima indeterminazione (vuoto squeezed), come mostrato in fig. 15.

La generazione di stati squeezed è possibile non solo con mezzi a nonlinearità quadratica, come nel caso dell'hamiltoniana [11] o [12], ma anche con mezzi a nonlinearità cubica, in cui l'hamiltoniana risulta

formula [

14]

Un modo semplice per comprenderne il motivo è il seguente. Scriviamo a e a‡ come somma del valore medio e di una fluttuazione, cioè

formula [

15]

e inseriamo le [15] nella [14]. Assumendo che le fluttuazioni siano molto più piccole dei valori medi (regime linearizzato delle fluttuazioni), possiamo trascurare i termini quartici e cubici nelle fluttuazioni. Tra i termini rimanenti, vi sono due termini che hanno esattamente la stessa forma dell'hamiltoniana [12].

Tornando ai mezzi quadratici, oltre all'amplificatore parametrico degenere è possibile considerare il caso non degenere, in cui l'hamiltoniana di interesse è data, invece che dalla [11], da

formula [

16]

fig. 16

dove a₀, a₁ e a₂ indicano gli operatori di annichilazione di fotoni per i campi di pompa, segnale e idler rispettivamente. In questo caso, un fotone del campo di pompa di frequenza ω₀ viene convertito in una coppia di fotoni (uno del campo segnale 1, l'altro del campo segnale 2) che differiscono per la loro frequenza (e in questo caso ω₁+ω₂=ω₀) e/o per la loro polarizzazione (fig. 16). Un'interazione del tipo [16] non conduce a stati squeezed nel senso descritto sopra, ma a un tipo diverso di stati non classici. I due fotoni (segnale 1 segnale 2) generati in ciascun processo elementare di conversione parametrica sono correlati quantisticamente tra loro, e ciò porta a molti aspetti quantistici fondamentali. In particolare, la presenza di questi fotoni gemelli fa sì che la differenza tra il numero totale di fotoni nel campo segnale 1 e quelli nel campo segnale 2 sia nulla in media, e presenti fluttuazioni ben al di sotto del livello di shot noise.

A partire dall'esperimento di R. Slusher e collab., realizzato presso i laboratori della A&T Bell Telephone nel 1985, sono state compiute diverse osservazioni sperimentali di stati squeezed in mezzi a nonlinearità sia cubica sia quadratica, in regime sia stazionario sia impulsato. Particolarmente importanti sono stati gli esperimenti di J. Kimble e collab. effettuati all'Università del Texas ad Austin con oscillatori parametrici degeneri, grazie ai quali è stato ottenuto uno squeezing superiore al 70%. Nei laboratori della NTT di Tokyo, il gruppo di Yamamoto ha dimostrato la possibilità di ottenere fluttuazioni subpoissoniane in laser a semiconduttore, con una spettacolare riduzione del rumore al di sotto del livello di shot noise. E. Giacobino, C. Fabre e collab. hanno dimostrato, nei laboratori Kastler-Brossel di Parigi, la riduzione del rumore quantistico nella differenza del numero di fotoni nell'oscillatore parametrico non degenere, dell'ordine dell'80% sotto il livello dello shot noise. Recentemente, nei laboratori dell'università di Costanza, I. Mlynek, S. Shiller e collab. hanno realizzato un oscillatore parametrico degenere monolitico che genera un fascio segnale, con una riduzione di 72 dB al di sotto del livello di shot noise; tale sorgente è in grado di emettere radiazione infrarossa squeezed in ampiezza per durate ben maggiori di 10 minuti.

Applicazioni degli stati squeezed

di Luigi Alberto Lugiato, Alice Sinatra

Rivelazione di onde gravitazionali

fig. 17

L'interesse applicativo degli stati squeezed della luce divenne significativo quando, nel 1981, fu suggerito il loro impiego in un interferometro destinato a rivelare le onde gravitazionali. La teoria prevede che un'onda gravitazionale al suo passaggio deformi lo spazio nel piano ortogonale alla direzione di propagazione in modo anisotropo. Per es., un'onda incidente normalmente su di un piano ove delle masse sono disposte lungo una circonferenza, deformerebbe periodicamente la circonferenza in un'ellisse. Per mettere in evidenza questo effetto, si può usare un interferometro di Michelson a due bracci disposti a 90° lungo una circonferenza (fig. 17). Ognuno dei due bracci è costituito da una cavità ottica e i due specchi A e B, che delimitano le cavità C_A e C_B, sono vincolati alle loro posizioni da deboli oscillatori armonici. Il passaggio di un'onda gravitazionale nel piano ortogonale all'interferometro accorcerebbe una cavità e allungherebbe l'altra, inducendo quindi una modulazione nella differenza delle intensità I_A e I_B uscenti dai due bracci dell'interferometro alla frequenza dell'onda gravitazionale.

La difficoltà di un esperimento di questo genere risiede nel fatto che l'interazione dell'onda gravitazionale con gli specchi è molto debole, con la conseguenza che i piccoli spostamenti degli specchi possono facilmente essere mascherati da ogni sorta di rumore presente nel sistema, incluse le fluttuazioni di punto zero degli specchi, che dunque vanno trattati come oscillatori quantistici. Indipendentemente dal rumore intrinseco legato al moto degli specchi, la luce utilizzata nell'interferometro è a sua volta un fattore limitante per la sensibilità dello strumento. Una prima limitazione deriva dal fatto che la misura finale sulla differenza delle intensità uscenti dai due bracci dell'interferometro è limitata dallo shot noise ovvero dalle fluttuazioni quantistiche della luce. Una soluzione semplice del problema, che non richiede l'uso di luce squeezed, consisterebbe nell'utilizzare laser più potenti in modo da aumentare il rapporto segnale/rumore. Sfortunatamente, tuttavia, questa scelta aumenta un'altra sorgente di rumore nel sistema, e precisamente la forza aleatoria sugli specchi dovuta alla pressione di radiazione. Un'analisi accurata del problema, che prenda in conto correttamente tutte le fonti di rumore, è stata effettuata solo recentemente. Il risultato dimostra non soltanto che a parità di potenza utilizzata la sensibilità dello strumento aumenta usando luce squeezed, ma anche che con una scelta ottimale della quadratura squeezed della luce è possibile aumentare la massima sensibilità dello strumento.

Misurazione di piccoli sfasamenti mediante luce squeezed

fig. 18

Una seconda applicazione degli stati squeezed riguarda la misurazione di piccoli sfasamenti della luce per mezzo di un interferometro. In fig. 18 abbiamo schematizzato un dispositivo per la misura di piccoli sfasamenti che utilizza un interferometro di Mach-Zender. Il fascio di luce iniettato nell'interferometro è diviso (da un primo specchio semitrasparente) in due parti che percorrono cammini indipendenti prima di essere ricombinate (da un secondo specchio semitrasparente) all'uscita del dispositivo. Una leggera variazione del cammino ottico in uno dei due bracci viene rivelata come differenza delle intensità dei due fasci uscenti dall'interferometro, inviando i due fasci uscenti a due fotomoltiplicatori F₁ ed F₂ e sottraendo le fotocorrenti corrispondenti.

Supponiamo di avere aggiustato la differenza di cammino ottico lungo i due bracci dell'interferometro in modo tale che la differenza delle intensità uscenti dall'interferometro 〈I₋〉 sia in media nulla. Inserendo uno sfasamento θ arbitrariamente piccolo in uno dei due bracci dovremmo dunque rivelare un segnale non nullo nella differenza delle intensità in uscita, cioè 〈I₋(θ)〉∙0. Nell'analisi di questo esperimento ideale non possiamo tuttavia dimenticare le fluttuazioni quantistiche alle quali è soggetta la luce in uscita dall'interferometro. A questo proposito dobbiamo notare che, anche nel caso in cui si inietti un solo campo nell'interferometro, il campo nello stato di vuoto entra nell'interferometro attraverso la porta non utilizzata del primo specchio semitrasparente; perciò il rumore nella luce uscente dipende a priori sia dalle fluttuazioni del campo iniettato sia da quelle del campo di vuoto.

Una quantità rilevante per la misura di un piccolo sfasamento θ, è data dal rapporto (detto rapporto segnale/rumore) tra il valore medio non nullo della differenza di intensità dei fasci uscenti 〈I₋(θ)〉 e la sua varianza ΔI₋. Il più piccolo sfasamento misurabile corrisponde a un rapporto segnale/rumore uguale a uno, ossia alla situazione in cui il piccolo effetto che vogliamo misurare è dello stesso ordine di grandezza del rumore a cui è soggetta la misura.

In uno schema interferometrico classico, in cui viene iniettato nell'interferometro un solo campo in uno stato coerente ∣α〉, il più piccolo sfasamento misurabile risulta dato da θ_min∼∣α∣⁻¹. Tale limite può essere tuttavia superato iniettando nella porta non utilizzata del primo specchio semitrasparente uno stato di vuoto squeezed come quello emesso da un oscillatore parametrico degenere.

Misure quantistiche non distruttive

Vengono chiamate quantistiche non distruttive (QND) le misurazioni, effettuate su un sistema quantistico, che non perturbino la variabile che si misura o, in altre parole, non ne cambino il valore. Come abbiamo già accennato, per soddisfare al criterio di 'non distruzione' e ottemperare nello stesso tempo alle leggi della meccanica quantistica e alle regole di indeterminazione, una misurazione QND è progettata in modo tale che il rumore introdotto da essa nel sistema, detto rumore di retroazione, rimanga confinato nella variabile coniugata alla variabile di interesse senza ricadere sulla variabile stessa.

Solitamente la misurazione QND è indiretta e avviene in due fasi successive: una prima fase corrisponde ad accoppiare il sistema S, al quale siamo interessati, a un secondo sistema M di supporto, detto metro, in modo che si creino delle forti correlazioni, mentre la seconda fase, che ha luogo quando i due sistemi S ed M hanno cessato di interagire e sono fisicamente separati, consiste nell'ottenere una misura diretta (e dunque distruttiva) sul metro M in modo da ricavare le informazioni sul sistema S in maniera non distruttiva. Nello schema accennato il rumore di retroazione viene introdotto nel sistema S durante la prima fase della misurazione. Supponendo di voler misurare in particolare una certa grandezza A del sistema S, è necessario che siano verificate due condizioni per aver una misura non distruttiva: che l'evoluzione della grandezza A non dipenda dalla variabile coniugata ad A, e che l'interazione tra i due sistemi S ed M non cambi il valore della grandezza A.

In o., il sistema quantistico sul quale si effettua la misurazione è generalmente un modo del campo elettromagnetico confinato in una cavità, oppure un fascio propagante di luce laser. Nel caso di un fascio propagante, la misurazione avviene accoppiando il fascio al quale siamo interessati, detto fascio segnale, con un secondo fascio, detto metro, in un mezzo ottico non lineare, e operando successivamente una misurazione diretta sul fascio metro.

fig. 19A

Criteri quantitativi e misurabili sperimentalmente per stabilire fino a che punto una misura reale sia non distruttiva sono stati definiti nel campo delle misure QND su fasci di luce, che è per molti aspetti legato al campo della riduzione del rumore quantistico in o. di cui ci siamo occupati finora. Immaginiamo che un segnale sia trasmesso da un fascio di luce lungo una linea di telecomunicazione, per es. sotto forma di modulazione della sua intensità. L'idea della misura non distruttiva è che diversi utenti posti lungo la linea possano leggere l'informazione senza degradare il segnale, in particolare senza alterarne il rapporto segnale/rumore (fig. 19A). Una seconda possibile applicazione di una misura QND in o. riguarda il caso in cui non siamo interessati a piccole modulazioni di intensità date dal segnale, bensì alle sue fluttuazioni quantistiche. Se siamo in grado di misurare le fluttuazioni del fascio segnale senza disturbarle, possiamo utilizzare l'informazione della misura per sopprimerle intervenendo successivamente sul fascio segnale (fig. 19B).

Uno schema di accoppiamento adatto a misurare le fluttuazioni di intensità di un fascio può essere realizzato, per es., sfruttando l'effetto Kerr incrociato, per il quale ciascun campo, nel passare attraverso il mezzo non lineare, acquisisce una fase proporzionale all'intensità dell'altro campo, permettendoci di leggere le fluttuazioni e modulazioni di intensità del fascio segnale nella fase del fascio metro. Nel regime linearizzato in cui le fluttuazioni quantistiche e le modulazioni classiche date al segnale sono piccole rispetto all'ampiezza dei campi medi, l'accoppiamento tra intensità del segnale e fase del metro si traduce in un accoppiamento tra due quadrature X_s e Y_m di segnale e metro rispettivamente.

Affinché una misura QND sia efficiente per l'applicazione rappresentata in fig. 19A, si richiedono due condizioni. La prima riguarda l'accuratezza della misura ed è quantificata da un coefficiente C_m che rappresenta la correlazione tra l'ampiezza del segnale in entrata X_sⁱⁿ che trasporta l'informazione e la fase del metro Y_m°^ut dalla quale vogliamo 'estrarre' l'informazione:

La seconda riguarda la proprietà di non distruzione della misura ed è quantificata dal coefficiente C_s che rappresenta la correlazione tra l'ampiezza del segnale in ingresso nel dispositivo QND X_sⁱⁿ e quella in uscita X_s°^ut:

fig. 20

Le varianze che appaiono nei denominatori delle frazioni che definiscono C_s e C_m servono per normalizzare i coefficienti, che sono in questo modo limitati tra 0 e 1. In una misura QND ideale si ha C_m=C_s=1. In analogia con l'impossibilità di ridurre il rumore quantistico in tutte le quadrature del campo contemporaneamente, la condizione C_m=C_s=1 può essere realizzata solo selezionando una specifica quadratura del campo segnale e dunque utilizzando un dispositivo QND sensibile alla fase. I risultati migliori che si possono ottenere con un dispositivo non sensibile alla fase, e che segnano la linea di demarcazione tra dominio 'classico' e dominio 'quantistico', sono raggiunti da un semplice specchio semitrasparente (fig. 20), per mezzo del quale si trova che C_m+C_s=1.

Esaminiamo ora la seconda possibile applicazione della misura QND rappresentata in fig. 19B. L'efficienza del dispositivo QND rispetto a questa applicazione è rappresentata da un terzo coefficiente V_s∣m, che rappresenta la varianza condizionale del fascio segnale in uscita dal dispositivo, dato il risultato di una misurazione effettuata sul fascio metro. Definita anch'essa in termini di correlazioni tra le quadrature di metro e segnale, tale varianza vale

e rappresenta il massimo squeezing che si può ottenere nel fascio segnale utilizzando l'informazione ricavata dal fascio metro, dove V_s∣m=1 corrisponde al livello di rumore per uno stato coerente; per una misura QND ideale dev'essere V_s∣m=0. Un aspetto importante dei tre coefficienti QND che abbiamo introdotto, è che essi sono legati semplicemente a quantità misurabili sperimentalmente come al trasferimento del rapporto segnale/rumore lungo le due vie: segnale in ingresso→metro in uscita e segnale in ingresso→segnale in uscita del dispositivo per i coefficienti C_m e C_s rispettivamente, o al minimo rumore ottenuto ricombinando le fotocorrenti provenienti dalle rivelazioni di metro e segnale per il coefficiente V_s∣m.

fig. 21

Numerosi esperimenti QND che utilizzano non linearità di tipo quadratico o cubico sono riusciti ad accoppiare due campi (segnale e metro) a livello delle fluttuazioni quantistiche ottenendo C_s+C_m>1 e V_s∣m〈1. La fig. 21 riporta i risultati del primo esperimento QND, e di quello che sinora ha riportato le prestazioni migliori.

bibliografia

D. Walls, in Nature, 1979, 280, p. 451.

S.M. Barnett, C.R. Gilson, in European journal of physics, 1988, 9, p. 257.

S. Reynaud, A. Heidmann, E. Giacobino et al., Quantum fluctuations in optical systems, in Progress in optics, ed. E. Wolf, 30° vol., Amsterdam 1992, pp. 1-85.

H.J. Carmichael, An open systems approach to quantum optics, Berlin 1993.

R. Slusher, B. Yurke, in Le Scienze, 1993, 70, p. 48.

Quantum optics, ed. D. Walls, G.J. Milburn, Berlin-Heidelberg 1994.