Cassini, ovale di

Cassini, ovale di

Cassini, ovale di o cassinoide, curva algebrica piana del quarto ordine, definibile come luogo geometrico dei punti P del piano le cui distanze da due punti fissi hanno prodotto costante, ovvero per i quali si ha

essendo F₁ e F₂ i due punti fissi (detti fuochi) e k ≠ 0 una costante reale. Assumendo come fuochi i punti F₁ = (−c, 0) e F₂ = (c, 0), con c > 0, l’ovale di Cassini ha equazione cartesiana (x ² + y ² + c ²)² − 4c ²x ² = k ². Si tratta di una curva algebrica piana del quarto ordine, chiusa e simmetrica rispetto a ciascuno degli assi cartesiani. La forma del grafico dipende dal rapporto k/c:

• se |k/c| > 1 è costituito da un singolo cappio connesso;

• se |k/c| < 1 è costituito da due cappi sconnessi;

• se |k/c| = 1 si riduce a una lemniscata.

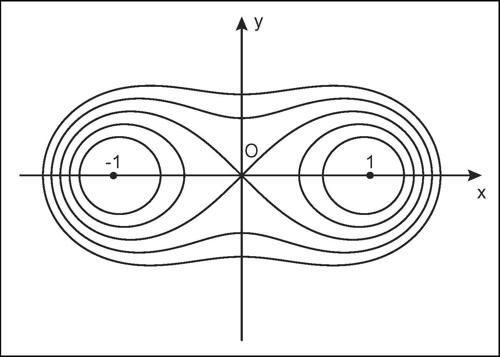
Nella figura sono rappresentati i grafici della curva ottenuti per c = 1 e per k = 0,6; 0,8; 1; 1,2; 1,4.