parabola
parabola
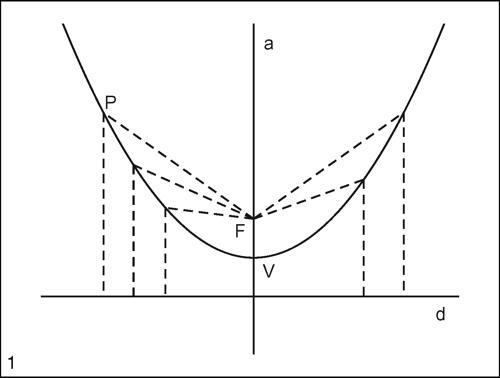
parabola curva algebrica piana del secondo ordine ottenuta sezionando la superficie di un cono circolare indefinito con un piano parallelo alla generatrice del cono. È pertanto una delle sezioni coniche o più semplicemente una → conica. È definita anche come luogo dei punti del piano equidistanti da un punto fisso F e da una retta fissa d, non passante per F. Il punto F e la retta d sono detti, rispettivamente, fuoco e direttrice della parabola. La retta a, passante per F e perpendicolare a d, è detta asse della parabola e il punto V in cui l’asse interseca la parabola è detto vertice della parabola. La parabola è una curva aperta, simmetrica rispetto al proprio asse, costituita da un solo ramo e avente due punti all’infinito reali e coincidenti che costituiscono la direzione del suo asse; è quindi tangente alla → retta impropria. Un’importante proprietà di questa conica, anche per le sue applicazioni, è la cosiddetta proprietà focale della parabola, che può essere così formulata: in ogni punto P di una parabola le bisettrici degli angoli di vertice P e aventi per lati la retta PF e la retta PP′ parallela all’asse e passante per P, sono la retta tangente in P alla parabola e la sua perpendicolare per P. Ciò vuol dire, in termini ottici, che in uno specchio parabolico ogni raggio uscente dal fuoco si riflette con direzione parallela all’asse (caratteristica utilizzata nel determinare la forma dei fari per automobili) e, viceversa, tutti i raggi paralleli all’asse che colpiscono la superficie riflettente al suo interno si riflettono convergendo in un solo punto, il fuoco (questa caratteristica è utilizzata nelle antenne paraboliche, nelle quali il segnale ricevuto si riflette, concentrandosi e potenziandosi, nel loro fuoco).
In coordinate cartesiane ortogonali non omogenee l’equazione di una parabola è
con a, …, ƒ ∈ R, a e c non entrambi nulli e con b2 − 4ac = 0. Assumendo come origine di un sistema cartesiano ortogonale il vertice, come asse delle ordinate l’asse della parabola e come asse delle ascisse la sua perpendicolare nel vertice, l’equazione della parabola è x 2 = 2py. Il valore assoluto del parametro p che compare in tale equazione rappresenta la distanza tra fuoco e direttrice.
Assumendo il fuoco come origine di un sistema di riferimento polare e come asse polare l’asse della parabola, l’equazione della parabola in coordinate polari è
In un riferimento cartesiano del piano Oxy, con l’asse delle ordinate parallelo all’asse della parabola, l’equazione assume la forma funzionale y = ax 2 + bx + c, con a ≠ 0 (forma canonica), detta equazione della parabola con asse parallelo all’asse delle ordinate. A seconda che il discriminante del trinomio ax 2 + bx + c sia positivo, nullo o negativo, la parabola risulta rispettivamente secante, tangente o priva di punti comuni all’asse delle ascisse. Il parametro a, detto parametro direttore, dà informazioni sulla concavità della parabola:
• se a > 0 la parabola ha la concavità rivolta nel verso positivo delle ordinate (concavità verso l’alto);
• se a < 0 la parabola ha la concavità rivolta nel verso negativo delle ordinate (concavità verso il basso).
Dai parametri a, b, c si possono ricavare gli elementi caratteristici della curva:
(coordinate del vertice)
(coordinate del fuoco)
(equazione dell’asse)
(equazione della direttrice)
Una parabola con asse parallelo all’asse delle ascisse ha invece equazione x = ay 2 + by + c, con a ≠ 0. Per una parabola con asse parallelo all’asse x sono valide tutte le considerazioni e le informazioni ricavate per una parabola con asse parallelo all’asse y, a patto di scambiare x con y e la posizione tra ascissa e ordinata nelle formule.
Se l’asse della parabola è parallelo a uno degli assi del riferimento cartesiano, la sua equazione è individuata da tre parametri a, b, c. Stabilito a quale degli assi di riferimento è parallelo il suo asse, la parabola è individuata assegnando tre condizioni semplici, per esempio il passaggio per tre punti non allineati. Pertanto, l’equazione della parabola passante per tre punti assegnati e di asse parallelo all’asse delle ordinate si ottiene risolvendo il sistema delle tre equazioni in a, b, c che si ottengono imponendo il passaggio per i tre punti.
Nel piano reale, le possibili posizioni reciproche di una parabola e una retta non parallela al suo asse sono:
• retta secante la parabola: ci sono due distinti punti di intersezione;
• retta tangente alla parabola: ci sono due punti di intersezione coincidenti;
• retta esterna alla parabola: non ci sono punti di intersezione.
Si osservi tuttavia che una retta parallela all’asse della parabola ha, nel piano euclideo, un solo punto di intersezione con la parabola stessa, essendo l’altro punto di intersezione il punto improprio che essa ha in comune con l’asse della parabola. Da un punto esterno a una parabola si possono tracciare due rette tangenti, da un punto sulla parabola una sola retta tangente, da un punto interno nessuna tangente. Se P(x0, y0) appartiene alla parabola, la tangente in P alla parabola y = ax 2 + bx + c, ha equazione y − y0 = (2ax0 + b)(x − x0).
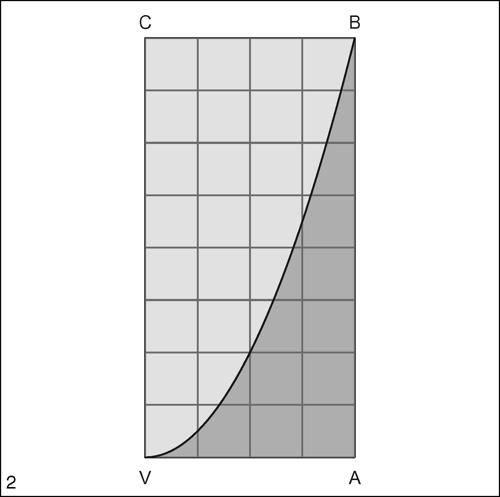
Come già individuato da Archimede di Siracusa, l’area della superficie sottesa a un arco di parabola, cioè della superficie delimitata dalla retta tangente alla parabola nel suo vertice, da una retta perpendicolare a questa e dall’arco di parabola così individuato, è uguale a 1/3 dell’area del rettangolo che ha per dimensioni i due segmenti di retta.